Abstract
The recent reported gravitational wave detection motivates one to investigate the properties of different black hole models, especially their behavior under (axial) gravitational perturbation. Here, we study the quasinormal modes of black holes in Weyl gravity. We derive the master equation describing the quasinormal radiation by using a relation between the Schwarzschild-anti de Sitter black holes and Weyl solutions, and also the conformal invariance property of the Weyl action. It will be observed that the quasinormal mode spectra of the Weyl solutions deviate from those of the Schwarzschild black hole due to the presence of an additional linear r-term in the metric function. We also consider the evolution of the Maxwell field on the background spacetime and obtain the master equation of electromagnetic perturbations. Then, we use the WKB approximation and asymptotic iteration method to calculate the quasinormal frequencies. Finally, the time evolution of modes is studied through the time-domain integration of the master equation.
Similar content being viewed by others
1 Introduction
From theoretical point of view, black hole is one of the most interesting and important solutions to gravity theories. The existence of such highly dense object in the cosmos has been also proved through the detection of gravitational waves (GWs) of black hole binary mergers [1] by the LIGO and VIRGO observatories and the captured image of the ‘shadow’ of a supermassive black hole by the Event Horizon Telescope collaboration [2, 3]. In this regard, it is interesting to investigate the other kinds of black hole solutions such as ones which are constructed based on higher curvature theories of gravity.
Weyl gravity, which its Lagrangian is defined by the square of the Weyl tensor, is one of the successful and interesting theories in higher derivative gravity scenario [4,5,6,7,8]. This model of gravity is invariant under local scale transformation of the metric \(g_{\mu \nu }(x)\rightarrow \Omega ^{2}(x)g_{\mu \nu }(x)\), and thus, it is unique up to the choice of the matter source in order to keep the conformal invariance property. The Weyl gravity suffers the Weyl ghost that it might be possible to remove it under certain conditions [9,10,11,12,13,14,15,16]. In addition, one can consider this theory of gravity as a suitable model for constructing quantum gravity [17, 18], since it is a higher-curvature theory of gravity which is power-counting renormalizable [19, 20].
From the viewpoint of high energy physics, it is shown that the Weyl gravity arises from twister-string theory with both closed strings and gauge-singlet open strings [21], and it appears as a counterterm in adS/CFT calculations [22,23,24]. In addition, this theory can be examined as a possible UV completion of Einstein gravity [25, 26]. It is worthwhile to mention that there is an equivalence between Einstein gravity and Weyl gravity by considering the Neumann boundary conditions [27, 28].
The discovery of GWs produced by the merger of compact binary objects [1, 29] added a totally different and new type of observations to the traditional astronomy based on electromagnetic waves. The emitted GWs contain a lot of information for fundamental physics and one can check the validity of the alternative theories of general relativity, such as massive gravity, scalar-tensor theory, and Weyl gravity. The signal of compact binary merger can be decomposed into three phases [30]. The first stage of a binary system is the inspiral phase which the frequency and amplitude of the signal chirp with time. During this phase, the signal is universal that just depends on the masses and the spins of compact objects and does not depend on the nature of source. The post-Newtonian approximation is a powerful tool for describing the inspiral phase [30]. The second stage is the merger phase and occurs after the inspiral phase with a rapid collapse of the two objects to form a black hole. The amplitude of GWs has a peak at this time and numerical relativity is used to compute the merger phase [31,32,33]. The ringdown phase is the final stage and describes the evolution of the new black hole. This new black hole is highly deformed due to the nonlinear dynamics of the collision. The perturbed black hole emits GWs in the form of quasinormal radiation and the perturbation theory can be used to calculate the quasinormal modes (QNMs) [34].
The ringdown phase of a compact binary merger might be better to study compared to the inspiral or merger phase depending on the physics being tested [35]. The nature of the binary components shows up only at high post-Newtonian order in the inspiral phase while investigating the merger phase requires time-consuming and theory-dependent numerical simulations. On the other hand, the ringdown phase can be appropriately investigated by perturbation theory and it is relatively simple to model beyond Einstein gravity. The perturbation theory of black holes was started by the pioneering work of Regge and Wheeler [36] and was continued by Zerilli [37]. They have found the wave equations of axial and polar perturbations of the Schwarzschild black hole and examined the dynamical stability of the black hole under small perturbations. The frequencies of perturbations are called the QN frequencies (QNFs) and have been calculated by using analytic and semi-analytic approaches [38,39,40,41], and also, several numerical methods [42,43,44,45,46] (see [47,48,49] for reviews on QNMs).
The electromagnetic and gravitational perturbations of the Schwarzschild black holes have been investigated in [50]. Besides, the QNMs for the gravitational and electromagnetic perturbations in modified gravity are calculated before [51]. In the case of conformal gravity, by imposing perturbations in Minkowskian spacetime, the GWs have been investigated and the effective energy-momentum tensor of the gravitational radiation is calculated [52]. The astrophysical GWs of inspiralling compact binaries have been investigated [53,54,55]. Moreover, the scalar, electromagnetic [56], and axial perturbations [57] of nonsingular black holes in conformal gravity have been studied. It was shown that it is possible to find the black hole solutions in Weyl gravity which are both thermally and dynamically stable under massive scalar perturbations, and also, the QNMs of this theory of gravity in asymptotically adS spacetime were obtained [58]. In addition, the nearly extreme black holes in Weyl gravity have been studied and an exact formula for the QNFs with an upper bound on them has been found [59].
In this paper, our main goal is studying the axial gravitational perturbations of singular black holes in Weyl gravity in order to investigate the QN radiation of the ringdown phase. We first obtain a master wave equation for an arbitrary metric which is conformally related to the Schwarzschild-(anti) de Sitter (Schwarzschild-(a)dS) spacetime. Then, by using the Weyl invariance property of the action, and also, the relation between the Schwarzschild-(a)dS black holes and Weyl solutions, we derive the wave equation of the axial gravitational perturbations of black holes in Weyl gravity. In addition, we consider both the scalar and electromagnetic perturbations in the background spacetime of these black holes. Then, we calculate the QNMs by employing the sixth order WKB approximation and the asymptotic iteration method (AIM). The time evolution of modes is also investigated by using the discretization scheme.
2 Four-dimensional black holes in Weyl gravity
Here, we give a brief review on the four-dimensional black holes in Weyl gravity and the connection between these solutions and the Schwarzschild-(a)dS black holes. The action of Weyl gravity is given by [60]
where \(C_{\mu \nu \rho \sigma }\) is the Weyl conformal tensor with the following explicit form
and the field equations can be obtained by taking a variation with respect to the metric tensor \(g_{\mu \nu }\)
which \(W_{\mu \nu }\) is the Bach tensor. It is straightforward to show that the following 4-dimensional line element satisfies all components of Eq. (3)
where the metric function is as follows
in which b, c, and d are three integration constants. It is notable that in contrast with the Einstein gravity that the cosmological constant should be considered in the action by hand, it is present as an integration constant in the Weyl gravity solutions. It is also worthwhile to mention that one can recover the Schwarzschild-(a)dS black hole by setting \(c=1\), \( d=-2M\), and \(b=-\Lambda /3\).
On the other hand, the line element describing the Schwarzschild-(a)dS spacetime in the radial coordinate \(\rho \) is given by
in which the metric function is
where M denotes the total mass of the black hole and \(\Lambda \) is the cosmological constant. One can show that there is a conformal relation between the black hole spacetimes in Weyl gravity (4) and Einstein theory (6). Indeed, these two spacetimes can be connected to each other by introducing a conformal factor \(S(\rho )\) so that \(ds^{2}=S(\rho )d {\tilde{s}}^{2}\). Every spacetime like Schwarzschild-(a)dS case which is conformally related to (4) is also a solution of the field equations of Weyl gravity (3) since all the metrics that transform conformally are equivalent. By considering the conformal factor \(S(\rho )=\left( 1+q\rho \right) ^{-2}\) [60], one can find the relation \(\rho =r\left( 1-qr\right) ^{-1}\) between the radial coordinates \(\rho \) and r. Multiplying (6) by the conformal factor \(S(\rho )\) and replacing \( \rho \) by r, we can obtain the following relations between the parameters [60]
where q is an arbitrary constant and we used \(\partial _{\rho }=\left( 1-qr\right) ^{2}\partial _{r}\). Therefore, we have a spectrum of conformal solutions depending on the values of q. We shall use these relations to obtain the axial perturbation of Weyl gravity in the coming section.
3 Gravitational perturbations of Weyl gravity
Here, we are going to obtain a master equation for the axial gravitational perturbations of black holes described by the metric function (5). First, one may note that there is a conformal relation between the line element (4) and the Schwarzschild black holes in asymptotically adS spacetime. Indeed, the spacetime of Weyl solutions and the spacetime of Schwarzschild-(a)dS solutions are related to each other as \(ds^{2}=S(\rho )d {\tilde{s}}^{2}\) so that \(ds^{2}\) is the line element of Weyl gravity (4 ), \(d{\tilde{s}}^{2}\) is the line element of the Schwarzschild-(a)dS black holes (6), and \(S(\rho )\) is the conformal factor. Thus, if we obtain the master equation of black holes conformally related to the Schwarzschild-(a)dS black holes, it can also describe the gravitational perturbations of Weyl solutions by replacing the explicit form of \(S(\rho )\) . In other words, if we construct the axial perturbations of \(S(\rho )d {\tilde{s}}^{2}\) (for the general form of \(S(\rho )\)), it is equivalent to the master equation of Weyl solutions. It is worthwhile to mention that it is not possible to construct a second-order master wave equation by considering small perturbations in (4) and using the field equations (3) because there is fourth-order differential in the field equations and the linearized field equations are fourth-order. Here, since our goal is to find a second order wave equation for Weyl solutions, we shall use the conformal relation between Schwarzschild-(a)dS black holes and Weyl solutions.
The gravitational perturbations of black holes conformally related to the Schwarzschild-(a)dS spacetime, i.e. the perturbations of \(S(\rho )d{\tilde{s}} ^{2}\), is derived in the Appendix 1. The master equation of the axial perturbations of the following spacetime (see Appendix 1)
is given by
where \(\omega \) is the QN frequency, \(\rho _{*}=\int \ g^{-1}\left( \rho \right) d\rho \) is the tortoise coordinate, and the effective potential \( V_{g}\left( \rho _{*}\right) \) reads
in which \(Z=\rho \sqrt{S\left( \rho \right) }\). Note that the right-hand side of (9) is exactly equal to the Weyl gravity spacetime (4) under the conditions (8) whenever we consider the conformal factor \(S(\rho )=\left( 1+q\rho \right) ^{-2}\). As a result, if we consider a coordinate transformation (in (9)-(11)) obeying this conformal factor, we can obtain the axial perturbations of singular black holes in Weyl gravity. Thus, we apply the coordinate transformation \(\rho \) to r so that \(S(\rho )=\left( 1+q\rho \right) ^{-2}\) and \(\rho =r\left( 1-qr\right) ^{-1}\). By considering \(\partial _{\rho }=\left( 1-qr\right) ^{2}\partial _{r}\) and \(\partial _{r_{*}}=g\left( \rho \right) \left( 1-qr\right) ^{2}\partial _{r}\), one can find the wave equation (10) converts into
where \(r_{*}\) is the new tortoise coordinate as \(dr/dr_{*}=\left( 1-qr\right) ^{2}\ {\bar{f}}\left( r\right) \) with
The effective potential (11) now is given by
which we used \(Z=r\) and \(\partial _{\rho }=\left( 1-qr\right) ^{2}\partial _{r}\). Therefore, Eq. (12) is the master equation of the axial perturbations of black holes in the Weyl gravity (5). In addition, Eq. (14) is the effective potential of perturbations and the free parameters b, c, and d of (5) are related to the parameters of (13) through the conditions (8). It is worthwhile to mention that for \(q=0\), the potential (14) reduces to
which is the effective potential of the axial perturbations of the Schwarzschild-(a)dS black hole [61], as we expected.
In order to get rid of the free parameter q in (14), one can apply the conditions (8) in (14) to obtain the following effective potential
which is a function of the free parameters of conformal gravity ( \(r_{*}=\int \ f^{-1}\left( r\right) dr\) being the tortoise coordinate). Now, we can recover the axial perturbations of the Schwarzschild-(a)dS black hole (15) by setting \(c=1\), \(d=-2M\), and \(b=-\Lambda /3\) in (17).
4 Scalar perturbations
Now, in order to ensure that our calculations of obtaining the axial perturbations of Weyl gravity are correct, we compare the effective potential of the massless scalar perturbations of black holes in Weyl gravity obtained by two methods; one is considering the evolution of a scalar field in the spacetime background (4) directly, and the other one is multiplying the Schwarzschild spacetime by a conformal factor (9) and obtaining the related effective potential.
The wave equation and the effective potential of a massless scalar perturbation in the spacetime background (4) are given by [59]
where \(r_{*}=\int \ f^{-1}\left( r\right) dr\) is the tortoise coordinate. On the other hand, the wave equation and the effective potential of the perturbative conformally related Schwarzschild-(a)dS black holes in \( \rho \) coordinate are as follows [56]
where \(Z=\rho \sqrt{S\left( \rho \right) }\) and \(\rho _{*}=\int \ g^{-1}\left( \rho \right) d\rho \) is the tortoise coordinate. Now, we apply the coordinate transformation \(\rho \) to r so that \(S(\rho )=\left( 1+q\rho \right) ^{-2}\) and \(\rho =r\left( 1-qr\right) ^{-1}\), as was described. Thus, the effective potential (21) reduces to
It is straightforward to show that \(\left( 1-qr\right) ^{2}{\bar{f}}\left( r\right) \) is equal to the metric function of Weyl gravity (5) with the help of obtained conditions (8), and thus the effective potential (22) is equal to Eq. (19). Therefore, this comparison of scalar perturbations shows that our calculations of obtaining the axial perturbations of Weyl solutions given in the previous section are indeed correct.
5 Electromagnetic perturbations
The wave equation and effective potential of electromagnetic perturbation in the spacetime background (4) are given by (see Appendix 2)
where \(r_{*}=\int \ f^{-1}\left( r\right) dr\) is the tortoise coordinate. On the other hand, the master equation of the perturbative conformally related Schwarzschild-(a)dS black holes in \(\rho \) coordinate is [56]
with
where \(\rho _{*}=\int \ g^{-1}\left( \rho \right) d\rho \) is the tortoise coordinate. By applying the coordinate transformation \(\rho \) to r such that \(S(\rho )=\left( 1+q\rho \right) ^{-2}\) and \(\rho =r\left( 1-qr\right) ^{-1}\), the effective potential (26) reduces to
which \(\left( 1-qr\right) ^{2}{\bar{f}}\left( r\right) \) is equal to the metric function of Weyl gravity (5) by considering the conditions (8). Therefore, the effective potentials (24) and (27) are the same.
It is worthwhile to mention that scalar, electromagnetic, and gravitational perturbations of Weyl gravity can be collected and described by the following master equation
with the potential
where \(s=0,1,2\) is the spin of the perturbing field and we used the effective potentials given in Eqs. (17), (19), and (24) to obtain this equation. By inserting \(c=1\), \(d=-2M\), and \(b=-\Lambda /3\) into ( 29), one can obtain
for the Schwarzschild-(a)dS black holes [48].
6 Quasinormal modes
Here, we consider the master equation (28) with the effective potential (29) for \(s=0,1,2\) as the results of perturbations of Weyl gravity. The spectrum of QNMs is the solution of the wave equation (28) and this spectrum becomes discrete when we impose some proper boundary conditions. The boundary conditions are applied to the modes \(\Psi \left( r_{*}\right) \) at \(r_{*}\rightarrow \pm \infty \) which can be obtained by studying the flux of radiation detected by physical observers near the event horizon and cosmological horizon. The observers detect outgoing waves at the cosmological horizon and incoming radiation at the event horizon
where \(r_{e}\) is the event horizon and \(r_{c}\) denotes the cosmological horizon.
Now, we concentrate our attention on the conformal-dS solutions (\(b<0\)) and calculate the QN frequencies by using the WKB formula as a semi-analytic approach and AIM as a numerical method. The WKB approximation is based on the matching of WKB expansion of the modes \(\Psi \left( r_{*}\right) \) at the event horizon and cosmological horizon with the Taylor expansion near the peak of the potential barrier. This method can be used for an effective potential that forms a potential barrier with a single peak. It was first applied to the problem of scattering around black holes [39], and then extended to the 3rd order [40], 6th order [41], and 13th order [63]. The WKB formula is given by
where n is the overtone number, \(V_{0}\) is the value of the effective potential at its local maximum, and \(\Omega _{k}\)’s denote the kth order of the approximation and depend on the value of the effective potential and its derivatives at the local maximum. It is notable that the explicit form of the WKB corrections is given in [40, 41]. We shall use this formula up to the sixth order as a semi-analytical approach to obtain the QNFs of perturbations.
On the other hand, the AIM has been employed for solving the eigenvalue problems and second-order differential equations [64, 65]. It was also shown that the improved AIM can be used as an accurate numerical method for calculating the QNMs [45, 66]. Here, we will use this method up to 15 iterations as a numerical approach to obtain the QNFs of perturbations.
In addition, we can investigate the contribution of all modes by using the time-domain integration of the wavelike equation (28). The time-domain profile of modes shows the time evolution of modes at the ringdown stage and the behavior of the asymptotic tails at late times. In order to obtain the time evolution of modes, we follow the discrimination scheme given in [67]. The perturbation equation (28) takes the following form
in terms of the light-cone coordinates \(u=t-x\) and \(v=t+x\), and \(\Psi \) assumed to have time dependence \(e^{-i\omega t}\). We can obtain the time-domain profile of modes by integrating this equation on the small grids from the two null surfaces \(u=u_{0}\) and \(v=v_{0}\). One can obtain the evolution equation in the light-cone coordinates by applying the time evolution operator on \(\Psi \left( u,v\right) \) and expanding this operator for sufficiently small grids
which \(\Delta \) is the step size of the grids. We shall obtain the time evolution of perturbations with a Gaussian wave packet on the surfaces \( u=u_{0}\) and \(v=v_{0}\) as initial data.
The QNFs of scalar (\(s=0\)), electromagnetic (\(s=1\)), and gravitational (\(s=2\) ) perturbations are presented in Tables 1, 2, 3 and 4. We calculated the lowest frequencies (Tables 1, 2) and the second overtone (Tables 3, 4) for some values of the free parameters b, c, d, and \(\ell \). The frequencies are written as \(\omega =\omega _{r}-i\omega _{i}\) where \(\omega _{r}\) (\(\omega _{i}\)) is the real (imaginary) part of the frequencies. The obtained frequencies for gravitational perturbation show that the WKB formula and the AI method are in a good agreement. The modes of gravitational perturbation live longer with lower frequency compared to the scalar and electromagnetic perturbations. In addition, the all kinds of perturbations decay faster with more oscillations by increasing d and/or b. However, the effective potential is positive and all frequencies have a negative imaginary part which indicates that these kinds of perturbations will decay with time, and thus, the spacetime is stable.
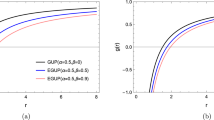
The time-domain profile of modes for different perturbations is presented in Figs. 1 and 2 for some fixed values of the free parameters. According to the Fig. 1, we can observe that the QN oscillations of the wave function \(\Psi \left( t,r\right) \) at the ringdown phase of gravitational perturbations for early and intermediate times. This figure confirms that the wave function oscillates with a frequency that increases and decay faster with increasing b and/or d. In addition, the time evolution of modes for scalar and electromagnetic perturbations is illustrated in Fig. 2. This figure shows that the QN oscillations of gravitational perturbation live longer with lower frequency compared to the scalar and electromagnetic perturbations.
This figure evaluated at \(r=2\) for \(\ell =2\), \(b=-0.1\), and \(c=0.3\) . It shows the QN modes of scalar (\(s=0\)) and electromagnetic (\(s=1\)) perturbations alongside the gravitational ones (\(s=2\)). By comparing the left panel and right panel we find that the modes of all perturbations decay faster with more oscillations by increasing d
\(Re[\omega ]\) and \(Im[\omega ]\) as a function of c for \(\Lambda =0.02\) and unit mass calculated by using the sixth order WKB formula. The vertical line indicates the frequencies of the Schwarzschild-dS black hole. Both the real and imaginary parts of QN frequencies decrease whenever c deviates from one
In order to obtain the deviations of Weyl solutions from the Schwarzschild-dS black holes, we compare the QNM spectra of the both cases. To do so, we first consider \(d=-2M\) and \(b=-\Lambda /3\) in the metric function (5), and then calculate the gravitational QN modes. In this way, the metric function of conformal gravity takes the form
and thus, the value of c characterizes the deviation. As c gets away from 1, both the real and imaginary parts of frequencies decrease which shows that the perturbations in the conformal black holes’ background live longer compared to the Schwarzschild ones (see Fig. 3). It is notable that in order to have black hole solutions, the value of c cannot be chosen from \(c\le -0.5\) and \(c\ge 2\), and also, the allowed range for nearly extreme black holes is \(-1<c<2\) [59].
In addition, the exact relation for QNFs in the eikonal limit (\(\ell \rightarrow \infty \)) can be obtained by the first order WKB formula (32)
and in this regime, the effective potential (29) is given by
which is still a function of c due to the presence of \(f\left( r\right) \). Interestingly, we find that these black holes, unlike the non-singular black holes in conformal gravity [57], can be distinguished from the Schwarzschild ones even in the eikonal limit.
6.1 Error estimation of QN frequencies
Although the WKB formula gives the best accuracy at \(\ell >n\) and gives us an accurate and economic way to compute the QN frequencies, this method does not always give a reliable result and neither guarantees a good estimation for the error [41, 68]. In addition, we cannot always increase the WKB order to obtain a better approximation for the frequency. In practice, there is some order that the WKB formula (32) provides the best approximation, and the error increases as the order of the formula increases. On the other hand, since the AIM relies upon a specialized barrier function, there is no systematic way to estimate the errors or to improve the accuracy [45]. In order to estimate the error of the WKB approximation, we can compare two sequential orders of the formula (32). However, since each WKB order correction affects either real or imaginary part of the squared frequencies, we should use the following quantity
for the error estimation of \(\omega _{k}\) that is calculated with the WKB formula of the order k. This quantity allows determining the WKB order in which the error is minimal. In the case of the Schwarzschild black holes, it is shown that the error estimation (38) provides a very good estimation of the error order, satisfying [68]
where \(\omega \) is an accurate value of the QN frequency calculated by using numerical methods. Thus, we can use the error estimation (38) to find the order of the absolute error and determine the order which gives the most accurate approximation for the QN mode.
In the Tables 5 and 6, we summarize the error estimation of the WKB formula for the fundamental and first overtone QNMs of fixed \(\ell =2\), \( b=-0.08\), \(c=0.3\), and \(d=-1\) (related to the last line of Tables 1 and 3). From Table 5, we can see that the best order of the WKB formula for calculating the QN frequency of gravitational perturbations is 7th-order whereas the QN frequency of electromagnetic perturbations has the best accuracy with the help of 12th-order. In the case of scalar perturbations, the error of the WKB formula of 10th-order is minimal. Table 6 shows the same results for the first overtone frequency, except for gravitational perturbations. The QN frequency of gravitational perturbations has the best accuracy with the help of 8th-order. If we assume that the band (39 ) is also correct for the Weyl solutions, since the maximum estimation of the error for the 6th-order WKB formula is of order \(10^{-6}\) and \(10^{-5}\) , up to 4 (3) digits of the frequency in the last line of Table 1 (3) are reliable. Our calculations based on (39), not shown here due to economic reason, show that the frequencies given in Tables 1, 2, 3 and 4 are reliable up to a minimum of 3 digits.
7 Conclusions
We have investigated the effects of both the axial gravitational and electromagnetic perturbations on a black hole system in Weyl gravity. We have derived the master equation, describing the QN radiation, from the conformal invariance property of the Weyl action, and also, a relation between the Schwarzschild-(a)dS black holes and Weyl solutions. We have found that the QNM spectra of the Weyl solutions deviate from those of the Schwarzschild black hole due to the presence of a linear r-term in the metric function. We have seen that, unlike the non-singular black holes in conformal gravity, this deviation was present even in the eikonal regime. Thus, it will be possible to test the Weyl solutions (or at least find a constraint on the free parameter c in order to recover the present universe after a phase transition where the conformal symmetry is broken) with the help of future gravitational wave detectors. Moreover, it was shown that the perturbations in the conformal black holes’ background live longer compared to the Schwarzschild ones.
In addition, we have calculated the QN frequencies of scalar, electromagnetic, and gravitational perturbations through both the sixth order WKB approximation and the improved AIM after 15 iterations. For the obtained frequencies, the effective potential was positive and all the frequencies had a negative imaginary part. Therefore, one can obtain some stable black hole solutions in conformal gravity under these kinds of perturbations.
We have found that the QN modes of gravitational perturbations live longer with lower frequency compared to the scalar and electromagnetic perturbations. In addition, all kinds of perturbations decay faster with more oscillations by increasing the free parameters d and/or b. Furthermore, the time evolution of different perturbations for early and intermediate times is studied by using the time-domain integration of the master equation. The time-domain profile of modes confirmed the previous results mentioned above.
Data Availability Statement
This manuscript has no associated data or the data will not be deposited. [Authors’ comment: This research paper is a theoretical study of black holes and so no publishable data is involved.]
References
B.P. Abbott et al. (LIGO Scientific and Virgo Collaborations), Phys. Rev. Lett. 116, 061102 (2016)
K. Akiyama et al. (Event Horizon Telescope), Astrophys. J. 875, L1 (2019)
K. Akiyama et al. (Event Horizon Telescope), Astrophys. J. 875, L4 (2019)
R. Bach, Math. Z. 9, 110 (1921)
A. Buchdahl, Edinb. Math. Soc. Proc. 10, 16 (1953)
R.J. Riegert, Phys. Rev. Lett. 53, 315 (1984)
P.D. Mannheim, D. Kazanas, Astrophys. J. 342, 635 (1989)
H. Lu, C.N. Pope, Phys. Rev. Lett. 106, 181302 (2011)
P.D. Mannheim, A. Davidson, arXiv:hep-th/0001115
C.M. Bender, Rep. Prog. Phys. 70, 947 (2007)
C.M. Bender, P.D. Mannheim, Phys. Rev. D 78, 025022 (2008)
C.M. Bender, P.D. Mannheim, J. Phys. A 41, 304018 (2008)
C.M. Bender, P.D. Mannheim, Phys. Rev. Lett. 100, 110402 (2008)
P.D. Mannheim, Philos. Trans. R. Soc. A 371, 20120060 (2013)
P.D. Mannheim, Phys. Lett. B 753, 288 (2016)
P.D. Mannheim, J. Phys. A 51, 315302 (2018)
E. Bergshoeff, M. de Roo, B. de Wit, Nucl. Phys. B 182, 173 (1981)
B. de Wit, J.W. van Holten, A. Van Proeyen, Nucl. Phys. B 184, 77 (1981)
K. Stelle, Phys. Rev. D 16, 953 (1977)
F. Faria, Eur. Phys. J. C 76, 188 (2016)
N. Berkovits, E. Witten, JHEP 08, 009 (2004)
H. Liu, A.A. Tseytlin, Nucl. Phys. B 533, 88 (1998)
M. Henningson, K. Skenderis, JHEP 07, 023 (1998)
V. Balasubramanian, E.G. Gimon, D. Minic, J. Rahmfeld, Phys. Rev. D 63, 104009 (2001)
S.L. Adler, Rev. Mod. Phys. 54, 729 (1982)
G. ’t Hooft, Found. Phys. 41, 1829 (2011)
J. Maldacena, arXiv:1105.5632
G. Anastasiou, R. Olea, Phys. Rev. D 94, 086008 (2016)
B. Abbott et al. (LIGO Scientific and Virgo Collaborations), Phys. Rev. Lett. 119, 161101 (2017)
L. Blanchet, arXiv:1902.09801
F. Pretorius, Phys. Rev. Lett. 95, 121101 (2005)
M. Campanelli, C.O. Lousto, P. Marronetti, Y. Zlochower, Phys. Rev. Lett. 96, 111101 (2006)
J.G. Baker, J. Centrella, D.I. Choi, M. Koppitz, J. van Meter, Phys. Rev. Lett. 96, 111102 (2006)
E. Berti, V. Cardoso, C.M. Will, Phys. Rev. D 73, 064030 (2006)
L. Barack et al., Class. Quantum Gravity 36, 143001 (2019)
T. Regge, J.A. Wheeler, Phys. Rev. 108, 1063 (1957)
F.J. Zerilli, Phys. Rev. D 2, 2141 (1970)
V. Ferrari, B. Mashhoon, Phys. Rev. D 30, 295 (1984)
B.F. Schutz, C.M. Will, Astrophys. J. Lett. 291, L33 (1985)
S. Iyer, C.M. Will, Phys. Rev. D 35, 3621 (1987)
R.A. Konoplya, Phys. Rev. D 68, 024018 (2003)
S. Chandrasekhar, S. Detweiler, Proc. R. Soc. Lond. Ser. A 344, 441 (1975)
E.W. Leaver, Proc. R. Soc. Lond. Ser. A 402, 285 (1985)
G.T. Horowitz, V.E. Hubeny, Phys. Rev. D 62, 024027 (2000)
H.T. Cho et al., Adv. Math. Phys. 2012, 281705 (2012)
Y. Hatsuda, arXiv:1906.07232
K.D. Kokkotas, B.G. Schmidt, Living Rev. Relativ. 2, 2 (1999)
E. Berti, V. Cardoso, A.O. Starinets, Class. Quantum Gravity 26, 163001 (2009)
R.A. Konoplya, A. Zhidenko, Rev. Mod. Phys. 83, 793 (2011)
V. Cardoso, R. Konoplya, J.P.S. Lemos, Phys. Rev. D 68, 044024 (2003)
L. Manfredi, J. Mureika, J. Moffat, Phys. Lett. B 779, 492 (2018)
R. Yang, Phys. Lett. B 784, 212 (2018)
C. Caprini, P. Holscher, D.J. Schwarz, Phys. Rev. D 98, 084002 (2018)
P. Holscher, D.J. Schwarz, Phys. Rev. D 99, 084005 (2019)
F.F. Faria, Phys. Rev. D 99, 048501 (2019)
B. Toshmatov, C. Bambi, B. Ahmedov, Z. Stuchlik, J. Schee, Phys. Rev. D 96, 064028 (2017)
C.Y. Chen, P. Chen, Phys. Rev. D 99, 104003 (2019)
S. H. Hendi, M. Momennia, F. Soltani Bidgoli, arXiv:1807.01792
M. Momennia, S.H. Hendi, Phys. Rev. D 99, 124025 (2019)
H. Lu, Y. Pang, C.N. Pope, J.F. Vazquez-Poritz, Phys. Rev. D 86, 044011 (2012)
V. Cardoso, J.P.S. Lemos, Phys. Rev. D 64, 084017 (2001)
A. Zhidenko, Class. Quantum Gravity 21, 273 (2004)
J. Matyjasek, M. Opala, Phys. Rev. D 96, 024011 (2017)
H. Ciftci, R.L. Hall, N. Saad, J. Phys. A 36, 11807 (2003)
H. Ciftci, R.L. Hall, N. Saad, Phys. Lett. A 340, 388 (2005)
H.T. Cho, A.S. Cornell, J. Doukas, W. Naylor, Class. Quantum Gravity 27, 155004 (2010)
C. Gundlach, R.H. Price, J. Pullin, Phys. Rev. D 49, 883 (1994)
R.A. Konoplya, A. Zhidenko, A.F. Zinhailo, Class. Quantum Gravity 36, 155002 (2019)
S. Chandrasekhar, The Mathematical Theory of Black Holes (Oxford University, Oxford, 1983)
Acknowledgements
We wish to thank Shiraz University Research Council.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix A: Gravitational perturbations of black holes conformally related to the Schwarzschild-(a)dS solutions
Assume a black hole spacetime is conformally related to the Schwarzschild-(a)dS solutions so that
Multiplying the Schwarzschild spacetime by a conformal factor can be described by an anisotropic fluid with the following effective energy-momentum tensor [57]
where \(p_{1}\) and \(p_{2}\) are, respectively, the radial pressure and the tangential pressure, and \({\hat{\rho }}\) is the energy density measured by a comoving observer. The explicit expressions of \({\hat{\rho }}\), \(p_{1}\), and \( p_{2}\) are functions of \(\rho \) and they can be derived by calculating the corresponding field equations constructed from the line element (40). In addition, \(u^{\mu }\) is the timelike four-velocity and \(x^{\mu }\) is the spacelike unit vector (orthogonal to \(u^{\mu }\) and angular directions) and they satisfy
in which the indices are raised and lowered by the metric \({\hat{g}}_{\mu \nu } \), and we also assumed \(u^{\mu }=\left[ u^{t},0,0,0\right] \) and \(x^{\mu }= \left[ 0,x^{\rho },0,0\right] \) in the comoving frame.
In order to obtain the master wave equation and the effective potential of the line element (40), we follow Chandrasekhar and his notation is used [69]. The axial perturbations are characterized by introducing the non-vanishing parameters \(\sigma \), \(q_{2}\), and \(q_{3}\) in the unperturbed spacetime in the following form
in which \(\nu \), \(\psi \), \(\mu _{2}\), \(\mu _{3}\), \(\sigma \), \(q_{2}\), and \( q_{3}\) are functions of t, \(x^{2}\) (radial coordinate \(\rho \)), and \(x^{3}\) (polar angle \(\theta \)) so that \(\sigma \), \(q_{2}\), and \(q_{3}\) are small quantities. The components of the unperturbed metric (\(\sigma ,q_{2},q_{3}=0\) ) are as follows
The proper field equations, describing this unperturbed metric, are
where \(G_{\mu \nu }\) is the Einstein tensor. Here, following [57], we use the tetrad formalism to derive the master equation because the axial components of the perturbed energy-momentum tensor in the tetrad frame also vanish in this case, and thus, \({\hat{\rho }}\) , \(p_{1}\), and \(p_{2}\) have nothing to do with the master equation. The tetrad basis corresponding to the line element (43) is defined as follows
where the Greek letters (labelling the columns) are the tensor indices and Latin letters enclosed in parentheses (labelling the rows) are the tetrad indices run from 0 to 3. Based on this formalism, any vector or tensor field can be projected onto the tetrad frame to obtain its tetrad components
in which \(\eta _{(a)(b)}=e_{(a)}^{\mu }e_{\mu (b)}\) is a constant symmetric matrix. In the tetrad frame, the perturbed field equations (46) read
where the perturbed energy-momentum tensor is as follows
By considering the constraints (42) and \(u_{\mu }x^{\mu }=0\), we find that the axial components of the perturbed energy-momentum tensor in the tetrad frame vanish
Since the axial components of the perturbed energy-momentum tensor vanish, the master equation of the axial perturbations can be derived from
By substituting the line element (43) into (52), one can find (1, 2) and (1, 3) components as
where \(x^{0}=t\) and \(x^{1}=\varphi \), and we used \(Q_{AB}=q_{A,B}-q_{B,A}\). Considering the unperturbed values of \(\psi \) and \(\mu _{3}\) from (44), we obtain the pair of equations
which we used the new variable Q with the definition
By differentiating Eqs. (55) and (56) and eliminating \(\sigma \), we obtain
We now consider the following decomposition
where \(C_{\ell +2}^{-3/2}\left( \theta \right) \) is the Gegenbauer function governed by the following differential equation
Using (59) and (60), equation (58) reduces to
in which \(L=\left( \ell -1\right) \left( \ell +2\right) \). By introducing \( Q=Z\Psi ^{(-)}\), one can find that this equation converts to
where \(Z=\rho \sqrt{S(\rho )}\) and \(\rho _{*}=\int e^{-\nu +\mu _{2}}d\rho =\int g^{-1}\left( \rho \right) d\rho \) is the tortoise coordinate. Therefore, this is the master wave equation for axial gravitational perturbations of black holes conformally related to the Schwarzschild-adS spacetime by the conformal factor \(S(\rho )\). One may note that for \(S(\rho )=1\) (or \(Z=\rho \)), this equation reduces to
which is the wave equation of axial perturbations of the Schwarzschild-adS black holes [61], as it should be.
Appendix B: Electromagnetic perturbations of Weyl gravity
Here, we consider the evolution of the Maxwell field in Weyl gravity with the line element (4). The evolution is governed by Maxwell equations
where \(F_{\mu \nu }\) is the Faraday tensor and \(A_{\mu }\) is the electromagnetic potential. The four-potential \(A_{\mu }\) can be expanded in 4-dimensional vector spherical harmonics as [61]
where \(Y_{\ell m}\left( \theta ,\varphi \right) \) denotes the spherical harmonics. The first term in the right-hand side has parity \(\left( -1\right) ^{\ell +1}\) (axial sector of the expansion) and the second term has parity \(\left( -1\right) ^{\ell }\) (polar sector of the expansion). By substituting this expansion into the Maxwell equations (64), one can find a second-order differential equation for the radial part as (see [56] for details of calculations)
for both axial and polar sectors, and \(r_{*}=\int f^{-1}\left( r\right) dr\) being the tortoise coordinate. The mode \(\Psi \left( r_{*}\right) \) is a linear combination of the functions a(t, r), f(t, r), h(t, r), and k(t, r), but a different functional dependence based on the parity; for axial sector the mode is given by \(\Psi \left( r_{*}\right) =a(t,r)\) whereas for polar sector it is \(\Psi \left( r_{*}\right) =\frac{r^{2}}{ \ell (\ell +1)}\left[ \partial _{t}h(t,r)-\partial _{r}f(t,r)\right] \).
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Funded by SCOAP3
About this article
Cite this article
Momennia, M., Hendi, S.H. Quasinormal modes of black holes in Weyl gravity: electromagnetic and gravitational perturbations. Eur. Phys. J. C 80, 505 (2020). https://doi.org/10.1140/epjc/s10052-020-8051-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-020-8051-2