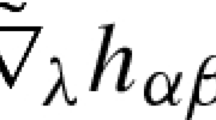Gauging scale symmetry and inflation: Weyl versus Palatini gravity

Abstract

We present a comparative study of inflation in two theories of quadratic gravity with gauged scale symmetry: (1) the original Weyl quadratic gravity and (2) the theory defined by a similar action but in the Palatini approach obtained by replacing the Weyl connection by its Palatini counterpart. These theories have different vectorial non-metricity induced by the gauge field ($w_\mu$) of this symmetry. Both theories have a novel spontaneous breaking of gauged scale symmetry, in the absence of matter, where the necessary scalar field is not added ad-hoc to this purpose but is of geometric origin and part of the quadratic action. The Einstein-Proca action (of $w_\mu$), Planck scale and metricity emerge in the broken phase after $w_\mu$ acquires mass (Stueckelberg mechanism), then decouples. In the presence of matter ($\phi _1$), non-minimally coupled, the scalar potential is similar in both theories up to couplings and field rescaling. For small field values the potential is Higgs-like while for large fields inflation is possible. Due to their $R^2$ term, both theories have a small tensor-to-scalar ratio ($r\sim 10^{-3}$), larger in Palatini case. For a fixed spectral index $n_s$, reducing the non-minimal coupling ($\xi _1$) increases r which in Weyl theory is bounded from above by that of Starobinsky inflation. For a small enough $\xi _1\le 10^{-3}$, unlike the Palatini version, Weyl theory gives a dependence $r(n_s)$ similar to that in Starobinsky inflation, while also protecting r against higher dimensional operators corrections.

1 Motivation

In this work we present a comparative study of inflation in two theories of quadratic gravity that have a gauged scale symmetry also known as Weyl gauge symmetry. This symmetry was first present in the original Weyl quadratic gravity [1,2,3] (for a review [4]) that follows from an underlying Weyl conformal geometry. This is relevant in early cosmology when effective theories at short distances may become conformal. Due to their symmetry, these theories have no mass scales or dimensionful couplings – these must be generated by the vacuum expectations values (vev) of the fields and this is the view we adopt here.

The first theory is the original Weyl quadratic gravity revisited recently in [5,6,7] with new results. This was in fact the first gauge theory (of scale invariance).¹ The second theory [8] has a similar action but in the Palatini formalism [9,10,11,12,13], which means replacing the Weyl connection by the Palatini connection. In the absence of matter the Lagrangian has the form

$$\begin{aligned} L_0=\sqrt{g} \Big \{ \,\frac{\xi _0}{4!} \, R({\tilde{\Gamma }},g)^2-\frac{1}{4\alpha ^2}\,R_{[\mu \nu ]}({\tilde{\Gamma }})^2\Big \} \end{aligned}$$

(1)

where ${\tilde{\Gamma }}$ is the Weyl or Palatini connection, respectively and $\xi _0$ and $\alpha$ are constants. These terms involve the (scalar and tensor) curvatures R and $R_{\mu \nu }$ which are functions of ${\tilde{\Gamma }}$; note that ${\tilde{\Gamma }}$ is not determined by the metric $g_{\mu \nu }$. This is the minimal action with such gauge symmetry. More quadratic terms may be present in both cases, see later.

In both theories the connection (${\tilde{\Gamma }}$) is Weyl gauge invariant. Hence this is not only a symmetry of the action, but also of the underlying geometry. Both theories have vectorial non-metricity which is due to the dynamics of the gauge field $w_\mu$ of scale symmetry;²$w_\mu$ is dynamical since for ${\tilde{\Gamma }}$ symmetric (which we assume to be the case) the term $R_{[\mu \nu ]}^2 \sim F_{\mu \nu }^2$ is just a gauge kinetic term of $w_\mu$. And if $w_\mu$ is not dynamical it can easily be integrated out and both theories are Weyl integrable and metric (${\tilde{\nabla }}_\mu g_{\mu \nu }=0$), see e.g. [5, 6, 8]. In both theories the Weyl gauge field is related to the trace of non-metricity: $w_\mu \propto g^{\alpha \beta }{\tilde{\nabla }}_\mu g_{\alpha \beta }$ where ${\tilde{\nabla }}$ is computed with the Weyl or Palatini connection. The two theories have however a different non-metricity tensor; this leads to different inflation predictions that we discuss. We thus have a link between non-metricity and inflation predictions.

Our study of these two theories with gauged scale symmetry is motivated by:

• (a) In the absence of matter both theories of quadratic gravity have spontaneous breaking of this symmetry as it was shown for the first time in [5, 6] for Weyl quadratic theory and in [8] for the Palatini theories. In both cases the Einstein-Proca action of $w_\mu$ and the Planck scale emerge in the broken phase, after $w_\mu$ becomes massive by “eating” the Stueckelberg field (would-be Goldstone/dilaton); this is the field that “linearises” $R({\tilde{\Gamma }},g)^2$ in the action, as we shall detail. After $w_\mu$ decouples near the Planck scale $M \sim \langle \mathrm{dilaton}\rangle$, the Einstein action is naturally obtained (together with metricity, see below).³ Thus, these theories provide a natural mass generation (Planck and $w_\mu$ masses) via a symmetry breaking mechanism. The above result is important since it shows a new mechanism of spontaneous breaking of scale symmetry (in the absence of matter) in which the necessary scalar field is not added ad-hoc to this purpose (as usually done); instead, the Stueckelberg field is here of geometric origin, being “extracted” from the $R({\tilde{\Gamma }},g)^2$ term. This situation is very different from previous studies that used instead e.g. modified versions of Weyl action that were linear-only in R and/or used additional matter field(s) to generate the Planck scale [19,20,21,22,23,24,25,26,27,28,29].

• (b) The breaking of Weyl gauge symmetry mentioned at a) is accompanied by a change of the underlying geometry (connection). For example in the Weyl theory after $w_\mu$ becomes massive it decouples, the Weyl connection becomes Levi-Civita, thus the underlying Weyl geometry becomes Riemannian and the theory becomes metric. A similar change of the underlying geometry happens in the Palatini case. Hence, the breaking of the Weyl gauge symmetry shown in [5, 6, 8] is not the result of a mere choice of a gauge (as it happens in Weyl or conformal theories with no Weyl gauge field), but is more profound: it is accompanied by both a Stueckelberg mechanism (as mentioned) and by transformations at a geometric level.

• (c) In both Weyl and Palatini theories $w_\mu$ has a large mass ($\sim M$) [5, 6, 8] so the associated non-metricity scale is very high; hence, non-metricity effects are suppressed by M. One thus avoids long-held criticisms [1] that had assumed a massless $w_\mu$ (implying metricity violation at low scales or path dependence of clock’s rates/rod’s length, in contrast to experience [30, 31]).

• (d) If matter is present e.g. a Higgs-like scalar is non-minimally coupled to $R({\tilde{\Gamma }},g)$, Weyl and Palatini theories have successful inflation, in addition to mass generation. The main goal of this work is to investigate comparatively their inflation predictions. We give new results in Sect. 3, such as the dependence $r(n_s)$ of the tensor-to-scalar ratio r on the spectral index $n_s$ in Weyl and Palatini cases and their relation to Starobinsky inflation [32,33,34].

• (e) The standard model (SM) with a vanishing Higgs mass has a Weyl gauge symmetry. It is well-known that the fermions and gauge bosons do not couple to the gauge field $w_\mu$ [35] but scalars (Higgs) have couplings to $w_\mu$. Having seen that $w_\mu$ is massive [5, 6, 8] it is worth studying the SM in Weyl quadratic gravity or its Palatini version.⁴ If the gauged scale symmetry is relevant for the mass hierarchy problem, it is intriguing that only the Higgs field couples directly to the gauge boson $w_\mu$ of scale symmetry.

• (f) $w_\mu$ is a dark matter candidate [36] and, being part of ${\tilde{\Gamma }}$, it could give a geometric solution to the dark matter problem. This brings together physics beyond SM and gravity.

• (g) The models with gauged scale symmetry do not have the unitarity issue (negative kinetic term) present in local scale invariant Lagrangians (without $w_\mu$), when generating the Einstein action from such Lagrangians: $L=(-1/12)\sqrt{g}\, [\phi ^2 R+ 6 (\partial _\mu \phi )^2]$. See [26] for a discussion on this issue in local scale invariant models⁵ [37,38,39,40,41,42,43]. In a gauged scale invariant model this negative kinetic term is cancelled and $\phi$ is “eaten” by $w_\mu$ which acquires mass [5, 6, 8] à la Stueckelberg [15, 44] and decouples, to recover the Einstein action and gauge.

• (h) In the gauged [5, 6, 8] and global [45,46,47] cases there is an associated non-zero conserved current, unlike in some local scale invariant models where this current is trivial [48, 49].

• (i) A gauged scale symmetry seems stable under black-hole physics unlike a global one [50], so it is preferable when building models that include gravity. Global models are easily made gauged scale invariant by replacing their Levi-Civita connection by e.g. Weyl connection. The theories discussed can give a gauged scale invariant version of Agravity global model [51, 52].

• (j) Another motivation to study theories with Weyl gauge symmetry is their geodesic completeness, as emphasized in [26]. In conformal invariant theories geodesic completeness can be achieved without the Weyl gauge vector presence, in the (metric) Riemannian universe; there, geodesic completeness or incompleteness is related to a specific gauge choice (with singularities due to an unphysical conformal frame) [53,54,55,56]. But Weyl gauge symmetry seems more profound: it is more than a symmetry of the action since, (unlike in conformal/Weyl invariant theory with no $w_\mu$), it is also a symmetry of the underlying geometry (of connection ${\tilde{\Gamma }}$). The geodesics in such case are determined by the affine structure. Differential geometry actually demands the existence of the Weyl gauge field [57] for the construction of the affine connection, because this ensures that geodesics are invariant (as required on physical arguments). After the breaking, $w_\mu$ decouples, see b) above, and we return to Riemannian geometry and geodesics are given by extremal proper time condition.⁶

The above arguments, a) to j), motivated our interest in theories beyond Standard Model (SM) with Weyl gauge symmetry. Section 2 reviews the two theories, showing their similarities and differences, see [5, 6, 8] for technical details. Section 3 studies comparatively their inflation predictions. The Appendix has technical details and an application to inflation.

2 Weyl versus Palatini quadratic gravity

2.1 The symmetry

Consider a Weyl local scale transformation $\Omega (x)$ of the metric $g_{\mu \nu }$ and of a scalar field $\phi _1$⁷

$$\begin{aligned} {\hat{g}}_{\mu \nu }=\Omega ^2 g_{\mu \nu },\quad \sqrt{{\hat{g}}}=\Omega ^4\sqrt{g},\quad \quad {\hat{\phi }}_1=\frac{1}{\Omega }\,\phi _1. \end{aligned}$$

(2)

To this geometric transformation one associates a Weyl gauge field $w_\mu$ that transforms as

$$\begin{aligned} {\hat{w}}_\mu =w_\mu -\partial _\mu \ln \Omega ^2. \end{aligned}$$

(3)

Equations (2), (3) define a gauged scale transformation. The symmetry is a gauged dilation group isomorphic to $R^+$ (non-compact). It differs from internal gauge symmetries, since $\Omega$ is real.

What is the relation of the Weyl field to the underlying geometry which is defined by $g_{\mu \nu }$ and ${\tilde{\Gamma }}$? One can define $w_\mu$ via the non-metricity, but it is more intuitive to define $w_\mu$ as a measure of the deviation of (the trace of) ${\tilde{\Gamma }}$ from the Levi-Civita connection:

$$\begin{aligned} w_\mu =(1/2)\,({\tilde{\Gamma }}_\mu -\Gamma _\mu (g)), \end{aligned}$$

(4)

with a notation ${\tilde{\Gamma }}_\mu ={\tilde{\Gamma }}_{\mu \nu }^\nu$ and $\Gamma _\mu =\Gamma _{\mu \nu }^\nu (g)$. $\Gamma _{\mu \nu }^\alpha (g)$ is the Levi-Civita connection for $g_{\mu \nu }$ while ${\tilde{\Gamma }}_{\mu \nu }^\alpha$ is the connection in either Weyl or Palatini gravity. We assume a symmetric connection ${\tilde{\Gamma }}_{\mu \nu }^\alpha ={\tilde{\Gamma }}_{\nu \mu }^\alpha$ (no torsion). Note that $w_\mu$ is a vector under coordinate transformation (${\tilde{\Gamma }}_\mu$ and $\Gamma _\mu$ are not). Finally, ${\tilde{\Gamma }}_{\mu \nu }^\alpha$ and in particular ${\tilde{\Gamma }}_\mu$ is invariant under (2), (3), in both Weyl and Palatini gravity (see also the Appendix). To check this invariance use (3) in (4) and that $\Gamma _\mu (g)=\partial _\mu \ln \sqrt{g}$; then $\Gamma _\mu ({\hat{g}})=\partial _\mu \ln (\sqrt{g}\,\Omega ^4)$. The change of the metric is compensated by that of $w_\mu$, leaving ${\tilde{\Gamma }}_\mu$ invariant.

2.2 The Lagrangian: Weyl versus Palatini

Consider next a Lagrangian with gauged scale invariance for a scalar field with non-minimal coupling, in Weyl and Palatini quadratic gravity. The analysis being similar, we present simultaneously both Weyl and Palatini theories. The main difference between them is in the coefficients ${\tilde{\Gamma }}_{\mu \nu }^\alpha$ which we do not need to specify right now. Consider then a (Higgs-like) scalar $\phi _1$ with non-minimal coupling $\xi _1 > 0$:

$$\begin{aligned} L= & {} \sqrt{g}\,\Bigg [\frac{\xi _0}{4!}\,R({\tilde{\Gamma }},g)^2 - \frac{1}{4 \alpha ^2}\, F_{\mu \nu }({\tilde{\Gamma }})^2 \nonumber \\&- \frac{1}{12} \,\xi _1\phi _1^2\,R({\tilde{\Gamma }},g) +\frac{1}{2} \,({\tilde{D}}_\mu \phi _1)^2 - \frac{\lambda _1}{4!}\phi _1^4\Bigg ], \end{aligned}$$

(5)

with a scalar curvature $R({\tilde{\Gamma }},g)$ which depends on the Weyl or Palatini connection ${\tilde{\Gamma }}$:

$$\begin{aligned} R({\tilde{\Gamma }},g)= & {} g^{\mu \nu }\,R_{\mu \nu }({\tilde{\Gamma }}),\nonumber \\ R_{\mu \nu }({\tilde{\Gamma }})= & {} \partial _\lambda {\tilde{\Gamma }}^\lambda _{\mu \nu }- \partial _\mu {\tilde{\Gamma }}^\lambda _{\lambda \nu } +{\tilde{\Gamma }}_{\rho \lambda }^\lambda {\tilde{\Gamma }}^\rho _{\mu \nu }-{\tilde{\Gamma }}^\lambda _{\rho \mu } {\tilde{\Gamma }}^\rho _{\nu \lambda }. \end{aligned}$$

(6)

${\tilde{\Gamma }}$ is invariant under (2), (3) so $R_{\mu \nu }({\tilde{\Gamma }})$ is invariant; $R({\tilde{\Gamma }},g)$ transforms covariantly, (A-10)

$$\begin{aligned} {\hat{R}}({\tilde{\Gamma }},{\hat{g}})=(1/\Omega ^2)\, R({\tilde{\Gamma }},g). \end{aligned}$$

(7)

With (7), the first and third term in L are invariant under (2), (3).

Further, the second term in L is a gauge kinetic term of $w_\mu$ and involves

$$\begin{aligned} F_{\mu \nu }({\tilde{\Gamma }})= {\tilde{\nabla }}_\mu w_\nu -{\tilde{\nabla }}_\nu w_\mu&=\partial _\mu w_\nu -\partial _\nu w_\mu \nonumber \\&=(\partial _\mu {\tilde{\Gamma }}_\nu -\partial _\nu {\tilde{\Gamma }}_\mu )/2. \end{aligned}$$

(8)

${\tilde{\nabla }}$ is defined by ${\tilde{\Gamma }}$ and in the second step we used that ${\tilde{\Gamma }}$ is symmetric. From (8) $F_{\mu \nu }$ is invariant under (2), (3), and one verifies that the second term in L is also invariant under these transformations. Since $F_{\mu \nu }({\tilde{\Gamma }})^2=\,R_{[\mu \nu ]}({\tilde{\Gamma }})^2$ where $R_{[\mu \nu ]}\equiv (R_{\mu \nu }-R_{\nu \mu })/2$, a gauged scale symmetry is naturally present in the Palatini version of $R^2+R_{[\mu \nu ]}^2$ gravity.

The Weyl-covariant derivative of $\phi _1$ in L and its transformation under (2), (3) are

$$\begin{aligned} {\tilde{D}}_\mu \phi _1=(\partial _\mu -1/2\,w_\mu )\,\phi _1,\quad \hat{{\tilde{D}}}_\mu {\hat{\phi }}_1=(1/\Omega )\, {\tilde{D}}_\mu \phi _1. \end{aligned}$$

(9)

Therefore $\phi _1$ is charged under the Weyl gauge symmetry. With (9) one checks that the kinetic term of $\phi _1$ is invariant under (2), (3). Finally, $\lambda _1\phi _1^4$ is the only potential term allowed by symmetry, so the entire L is invariant.

In the absence of matter  ($\phi _1$), L contains the first two terms only, giving the minimal action of the original Weyl quadratic gravity or its Palatini version; both actions have gauged scale symmetry and, after spontaneous breaking of this symmetry, one obtains the Einstein-Proca action for $w_\mu$, see [5, 6, 8]. If only the first term is present in L, both theories are Weyl integrable (metric) and Einstein action is obtained with a positive cosmological constant.

Returning to L, we replace the first term in (5) by $\xi _0 R({\tilde{\Gamma }},g)^2\rightarrow -\xi _0\,(2\, \phi _0^2\, R({\tilde{\Gamma }},g)+\phi _0^4)$ where $\phi _0$ is an auxiliary scalar; using the equation of motion of $\phi _0$ (of solution $\phi _0^2=-R$) recovers onshell the term $\xi _0\,R^2$ in (5). This gives a classically equivalent L, linear in R

$$\begin{aligned} L= & {} \sqrt{g}\,\Bigg [- \frac{1}{2} \,\rho ^2\,R({\tilde{\Gamma }},g) - \frac{1}{4 \alpha ^2}\,F_{\mu \nu }^2 \nonumber \\&+ \frac{1}{2} \,({\tilde{D}}_\mu \phi _1)^2 -{{\mathcal {V}}}(\phi _1,\rho ) \Bigg ], \end{aligned}$$

(10)

where

$$\begin{aligned} {{\mathcal {V}}}(\phi _1,\rho )= & {} \frac{1}{4!}\,\Bigg [\, \frac{1}{\xi _0} \big (6\rho ^2-\xi _1\phi _1^2\big )^2 + \lambda _1\phi _1^4\,\Bigg ],\quad \text {and}\nonumber \\ \rho ^2= & {} \frac{1}{6}\,\big (\xi _1\phi _1^2+\xi _0\phi ^2_0). \end{aligned}$$

(11)

We further replaced $\phi _0$ by radial direction $\rho$ in field space, so our new fields are now $\{\rho , \phi _1\}$.

L has similarities to a global scale invariant Higgs-dilaton model, Equations  (2.9), (2.10) of [47] also [59, 60]; $\phi _0$ has a large coupling ($\xi _0 > 1$) to R since the $R^2$ term has a perturbative coupling $1/\sqrt{\xi _0} < 1$ and this corresponds to a Higgs of non-minimal coupling $\xi _h > 1$ in [47].

The action in (10) depends on ${\tilde{\Gamma }}$ through its first three terms. We have two cases:

• (a) In Weyl quadratic gravity, ${\tilde{\Gamma }}$ is determined by $g_{\mu \nu }$ and the gauge field $w_\mu$, see its expression in Eq. (A-5) in the Appendix. Using this one replaces the scalar curvature in (10) in terms of the Ricci scalar of Riemannian geometry, Eq. (A-11). The result is Eq. (12) below.

• (b) In Palatini gravity, ${\tilde{\Gamma }}$ is simply determined by its equation of motion from the action in (10). After solving this Eq. [8], we obtain the connection shown in Eq. (B-2) in the Appendix; ${\tilde{\Gamma }}$ differs from that in Weyl case, due to different non-metricity (accounted for by $\gamma$ in Eq. (12)). With this ${\tilde{\Gamma }}$, one computes the scalar curvature,as usually done Eq. (B-5). Replacing this curvature back in action (10) one finds again L below (for ${\tilde{\Gamma }}$ onshell):

  $$\begin{aligned} L&=\sqrt{g}\Bigg \{ \frac{-1}{2} \Big [\rho ^2 R(g) + 6 (\partial _\mu \rho )^2\Big ] + 3 \gamma \,\rho ^2 (w_\mu -\partial _\mu \ln \rho ^2)^2 \nonumber \\&\quad -\frac{1}{4 \alpha ^2} \,F_{\mu \nu }^2 +\frac{1}{2} ({\tilde{D}}_\mu \phi _1)^2 - {{\mathcal {V}}}(\phi _1,\rho )\Bigg \} \end{aligned}$$

  (12)
  $$\begin{aligned}&\mathrm{where}\quad \gamma =1/4\,\,\, \mathrm {for\, Weyl\,\, case}; \quad \gamma =1\,\, \mathrm {for\, Palatini\,\, case.} \end{aligned}$$

  (13)

R(g) is the Ricci scalar for the metric $g_{\mu \nu }$. This is a metric formulation equivalent to the initial Lagrangian Eq. (5), invariant under transformations (2), (3); under these $\ln \rho$ transforms with a shift, $\ln \rho \rightarrow \ln \rho - \ln \Omega$, so $\ln \rho$ acts like a would-be Goldstone (“dilaton”), see later.

2.3 Einstein–Proca action as a broken phase of Weyl or Palatini gravity

Since L has a gauged scale symmetry, we should “fix the gauge”. We choose the Einstein gauge corresponding to constant $\rho$; this is obtained by using a transformation (2),(3) of a particular $\Omega = \rho /\langle \rho \rangle$ which is $\rho -$dependent and sets ${\hat{\rho }}$ to a constant ${\hat{\rho }}=\langle \rho \rangle$, and so introduces a mass scale. In terms of new variables (with a hat) Eq. (12) becomes

$$\begin{aligned} L= & {} \sqrt{{\hat{g}}}\, \Bigg \{-\frac{1}{2} M^2\,R({\hat{g}}) +3 \gamma \, M^2 {\hat{w}}_\mu {\hat{w}}^\mu \nonumber \\&-\frac{1}{4 \alpha ^2} {\hat{F}}_{\mu \nu }^2 +\frac{1}{2}(\hat{{\tilde{D}}}_\mu {\hat{\phi }}_1)^2 -{{\mathcal {V}}}({\hat{\phi }}_1,M)\Bigg \}, \end{aligned}$$

(14)

with $R({\hat{g}})$ the Ricci scalar for metric ${\hat{g}}_{\mu \nu }$, ${\hat{{\tilde{D}}}}_\mu {\hat{\phi }}_1=(\partial _\mu -1/2\,\,{\hat{w}}_\mu ){\hat{\phi }}_1$ and with $\nabla _\mu {\hat{w^\mu }}=0$; we denoted $M=\langle \rho \rangle$ which we identify with the Planck scale. The potential now depends on ${\hat{\phi }}_1$ only, see (11). This is the Einstein-Proca action for ${\hat{w_\mu }}$: this field has become massive of mass $m_w^2=6 \alpha ^2 \,\gamma \, M^2$ by absorbing the derivative of the Stueckelberg (would-be “dilaton”) field $\partial _\mu \ln \rho$; then the radial direction in field space ($\rho$) is not present anymore in the action. This is a spontaneous breaking of Weyl gauge symmetry; the number n of degrees of freedom other than the graviton ($n=3$) is conserved during this breaking: the initial massless scalar $\rho$ and massless vector $w_\mu$ are replaced by a massive gauge field $w_\mu$.

Note that in the absence of matter ($\phi _1$), the Stueckelberg field needed for breaking becomes $\ln \rho \propto \ln \phi _0$ and has a pure geometric origin, being simply “extracted” from the quadratic curvature term $R^2({\tilde{\Gamma }},g)$ in the initial, symmetric action. Therefore, one does not need to add this scalar field ad-hoc as usually done to this purpose, and the breaking and mass generation ($m_w$, Planck scale) takes place even in the absence of matter [5, 6, 8]. Finally, unless one is tuning the coupling $\alpha$ to small values, the mass of ${\hat{w_\mu }}$ is near the Planck scale.⁸

2.4 Scalar potential

To obtain a standard kinetic term for ${\hat{\phi }}_1$, similar to the “unitarity gauge” in the electroweak case, we remove the coupling ${\hat{w}}^\mu \partial _\mu {\hat{\phi }}_1$ from the term $(\hat{{\tilde{D}}}_\mu {\hat{\phi }}_1)^2$ in (14) by a field redefinition

$$\begin{aligned}&{\hat{w_\mu }} \rightarrow {\hat{w_\mu }}+ \partial _\mu \ln \cosh ^2 \Big [\frac{\varphi }{2 M\sqrt{6\gamma }}\Big ], \nonumber \\&{\hat{\phi }}_1 \rightarrow 2 M\sqrt{6\gamma }\,\sinh \Big [\frac{\varphi }{2 M\sqrt{6\gamma }}\Big ] \end{aligned}$$

(15)

In terms of the new fields Eq. (14) becomes

$$\begin{aligned} L= & {} \sqrt{{\hat{g}}}\, \Bigg \{ -\frac{1}{2} M^2 R ({\hat{g}}) + 3\gamma M^2 \cosh ^2 \Bigg [\frac{\varphi }{2 M\sqrt{6\gamma }}\Bigg ] \,{\hat{w}}_\mu {\hat{w}}^{\mu } \nonumber \\&-\frac{1}{4 \alpha ^2} {\hat{F}}^{ 2}_{\mu \nu } +\frac{{\hat{g}}^{\mu \nu }}{2}\partial _\mu \varphi \partial _\nu \varphi - V(\varphi ) \Bigg \}, \end{aligned}$$

(16)

which is ghost-free and

$$\begin{aligned} V(\varphi )= & {} V_0\, \Bigg \{ \Bigg [ 1-(4 \gamma )\,\xi _1\,\sinh ^2 \frac{\varphi }{2 M\sqrt{6\gamma }}\Bigg ]^2 \nonumber \\&+ (4 \,\gamma )^2\,\lambda _1 \xi _0 \,\sinh ^4\frac{\varphi }{2 M\sqrt{6\gamma }} \,\Bigg \},\quad V_0\equiv \frac{3}{2} \frac{M^4}{\xi _0}.\nonumber \\ \end{aligned}$$

(17)

Lagrangian (16) describes Einstein gravity, a scalar field $\varphi$ with canonical kinetic term and potential (17) that is $\gamma$-dependent, and a massive Proca field (${\hat{w_\mu }}$) that decouples near the Planck scale M. To make obvious the mass term of $w_\mu$ in (16) use that $\cosh ^2x=1+\sinh ^2x$. Equations (16), (17) can be extended to more scalar fields, see [6], Eq. 24].

For small field values $\varphi \ll M$, the potential in (17) becomes (recall that $M=\langle \rho \rangle$):

$$\begin{aligned} V(\varphi )&= \frac{3 \langle \rho \rangle ^4}{2\xi _0} -\frac{ 1}{2} \,\frac{\xi _1}{\xi _0}\,\langle \rho \rangle ^2\,\varphi ^2 \nonumber \\&\quad + \frac{ 1}{4!}\left[ \lambda _1 + \frac{\xi _1}{\xi _0}\left( \xi _1-\frac{1}{6\gamma }\right) \right] \,\varphi ^4 +{{\mathcal {O}}}(\varphi ^6/\langle \rho \rangle ^2). \end{aligned}$$

(18)

In this case the potential is similar in Weyl and Palatini cases, up to a small $\gamma$-dependence of the quartic coupling, negligible for (ultra)weak couplings $\xi _1 /\xi _0\ll 1$; in this case also the quadratic coupling is suppressed (recall the perturbative couplings are $1/\sqrt{\xi }_0 < 1$ and $\xi _1 < 1$).

If we identify $\varphi$ with the Higgs field, we have electroweak symmetry breaking, since $\xi _1>0$. For a classical hierarchy $\xi _1/\xi _0\ll 1$ one may be able to tune the mass of $\varphi$ near the electroweak scale $m^2=(\xi _1/\xi _0) \langle \rho \rangle ^2$. Gravitational corrections to $\lambda _1$ may be negative but there is no instability: the exact form of $V(\varphi )$ is positive, even if the self-coupling $\lambda _1=0$!

For large $\varphi$ the potential is different in Weyl and Palatini cases due to a different $\gamma$. This potential changed from initial (5) to (17) following two steps: the “linearisation” of the $R^2$ term by $\phi _0$ that induced the $\phi _0^4$ term, then transformation (15) which decoupled the (trace of) the connection from $\partial _\mu \phi _1$ and brought the presence of $\gamma$ i.e. non-metricity dependence.

Fig. 1

Left column: Weyl inflation plots; Right column: Palatini inflation plots. All figures have $\lambda _1 \xi _0=10^{-8}\le \xi _1^2$; Top plots: the potential $V/V_0$ in terms of $\varphi /M$ for different $\xi _1$; larger $\xi _1$ moves the curves to the left; larger $\lambda _1\xi _0$ lifts the minimum of the rightmost curves, see Eq. (17); middle plots: the plots $(n_s, N)$ for different $\xi _1$; bottom plots: the plots $(n_s,r)$ for different $\xi _1$; curves of $\xi _1=5\times 10^{-4}$ and $10^{-3}$ are degenerate; along these curves the value of N changes: the blue line segment has points of $55\le N\le 65$; red dots have $N=60$. The yellow (orange) area corresponds to the measured value of $n_s$ at $95 \%$ CL $(68 \%)$, respectively

3 Inflation

3.1 Weyl versus Palatini

We can now use Lagrangian (16) and potential $V(\varphi )$ of (17) to study inflation with $\varphi$ as the inflaton and compare its predictions for the Weyl ($\gamma =1/4$) and Palatini ($\gamma =1$) cases. For a previous study of inflation in the Weyl case, see⁹ [7, 76]. Lagrangian (16) describes a single scalar field in Einstein gravity and the usual formalism for a single-field inflation can be used. However, notice there exists a coupling of $\varphi$ to the Weyl field ${\hat{w_\mu }}$, the second term in (16). Hence, we must first show that this coupling and ${\hat{w_\mu }}$ do not affect inflation by $\varphi$.

Firstly, we do not consider here the possibility of the Weyl vector field itself as the inflaton¹⁰ since it could induce a substantial large-scale anisotropy [81] which would be in conflict with CMB isotropy. The anisotropy is obvious in the stress-energy tensor contribution of ${\hat{w_\mu }}$ which is not diagonal. This issue can be avoided if one considers a large number of randomly oriented vector fields or a triplet of mutually orthogonal vector fields [81], however this is not possible in the current fixed setup.

Secondly, one may ask if the Weyl field could play the role of a curvaton with $\varphi$ as the inflaton. The scenario of a vector field as a curvaton was discussed in detail in [82, 83]; in such scenario the vector field does not drive inflation (to avoid large scale anisotropy) but becomes important after inflation when it may dominate the Universe and imprint its perturbation spectrum. A scale invariant spectrum can be generated by ${\hat{w_\mu }}$ provided that during inflation the mass-squared of ${\hat{w_\mu }}$ is negative and large in absolute value ($\sim H^2$) while after inflation is positive and the vector field engages in oscillations and behaves as pressureless matter; this means it does not lead to large-scale anisotropy when it dominates [82, 83]. This scenario cannot apply here since $m^2_w$ is always positive. Indeed, the second term in (16)

$$\begin{aligned} \Delta L=\frac{1}{2} \sqrt{{\hat{g}}} f(\varphi )\, {\hat{w_\mu }} {\hat{w^\mu }}, \quad f(\varphi ) =6\gamma M^2 \cosh ^2\frac{\varphi }{2M\sqrt{\gamma }}. \end{aligned}$$

(19)

has $f(\varphi )>0$, for any value of $\varphi$ and the effective mass-squared of ${\hat{w_\mu }}$ is always positive.

Finally, in Friedmann–Robertson–Walker (FRW) universe ${\hat{g}}_{\mu \nu } = (1,-a(t)^2,-a(t)^2,-a(t)^2$, the vector field background compatible with the metric is ${\hat{w}}_\mu (t) = ({\hat{w}}_0(t),0,0,0)$. However, from the equation of motion of ${\hat{w}}_\mu$ one immediately sees that ${\hat{w_\mu }}(t) = 0$, (see also Eq. (C-13) for details). In this case $\Delta L$ is vanishing. Therefore, we are left with potential (17) and the usual formalism of single-field inflation in Einstein gravity applies, with $\varphi$ as inflaton.

One may ask what happens at the perturbations level? One easily sees that perturbations $\delta \varphi$ of $\varphi$ do not mix with perturbations $\delta {\hat{w_\mu }}$ (of longitudinal mode/Stueckelberg field $\rho$) of massive ${\hat{w_\mu }}$. Such mixing is in principle possible, with potential impact on inflation predictions, but it vanishes since it is proportional to ${\hat{w_\mu }}(t)(=0)$, as seen from expanding $\Delta L$ to quadratic level in perturbations: $\Delta L\propto {\hat{w^\mu }}(t) \,\delta \varphi \,\delta {\hat{w_\mu }}+\cdots$.¹¹ As a result, the coupling $\Delta L$ does not affect $\delta \varphi$ and the predictions of inflation by $\varphi$. For further discussion on perturbations $\delta \varphi$ and $\delta {\hat{w_\mu }}$ see Appendix 1 which supports these results.

The above arguments justify our use below of single-field slow-roll formulae¹²

$$\begin{aligned} \epsilon= & {} \frac{M^2}{2} \left\{ \frac{V^\prime (\varphi )}{V(\varphi )} \right\} ^2 = \frac{{4}}{3}\,\gamma \,\xi _1^2\, \sinh ^2 \frac{\varphi }{M\sqrt{6\gamma }} +{{\mathcal {O}}}(\xi _1^3),\, \end{aligned}$$

(20)

$$\begin{aligned} \eta= & {} M^2\,\frac{V^{\prime \prime }(\varphi )}{V(\varphi )} = -\frac{2}{3}\,\xi _1 \,\cosh {\frac{\varphi }{M\sqrt{6\gamma }}} \nonumber \\&+\frac{8}{3} \gamma \,\xi _1^2 \sinh ^2 \frac{\varphi }{2 M\sqrt{6\gamma }} +{{\mathcal {O}}}(\xi _1^3),\, \end{aligned}$$

(21)

The number of e-folds is

$$\begin{aligned} N= & {} \frac{1}{M^2} \int _{\varphi _e}^{\varphi _*} d\varphi \,\,\frac{V(\varphi )}{V^\prime (\varphi )} = \left\{ -\frac{3}{4\, \xi _1}\ln \tanh ^2\frac{\varphi }{2 M \sqrt{6\gamma }} \right. \nonumber \\&\left. + 3\gamma \ln \cosh ^2\frac{\varphi }{2 M \sqrt{6\gamma }}\right\} \Big \vert _{\varphi =\varphi _e}^{\varphi =\varphi _*}. \end{aligned}$$

(22)

with the last step in (20), (21), (22) valid in the leading approximation $\lambda _1\xi _0\ll \xi _1^2$ needed for a deep enough minimum for inflation; $\varphi _e$ is determined by $\epsilon (\varphi _e)=1$ and $\varphi _*$ is the initial value of the scalar field. Further, the scalar spectral index

$$\begin{aligned} n_s\,= & {} \, 1 + 2\,\eta _* - 6\, \epsilon _*= 1 - \frac{4}{3}\,\xi _1 \,\cosh \frac{\varphi _*}{M\sqrt{6\gamma }} + \frac{8}{3}\,\xi _1^2\,\gamma \, \nonumber \\&\times \Big [\cosh ^2 \frac{\varphi _*}{M\sqrt{6\gamma }} -1 \Big ] + {{\mathcal {O}}}(\xi _1^3).\, \end{aligned}$$

(23)

With the tensor-to-scalar ratio $r=16 \epsilon _*$, then from (20), (21), (23)

$$\begin{aligned} r={12}\,\gamma \, (1- n_s)^2 -\frac{64\gamma }{3}\, \xi _1^2+{{\mathcal {O}}}(\xi _1^3). \end{aligned}$$

(24)

The non-minimal coupling is reducing r, for fixed $n_s$. If we ignore the term $\propto \xi _1^2$ and higher orders, then the Palatini case ($\gamma =1$) has a larger r than Weyl theory ($\gamma =1/4$), for the same $n_s$. This is confirmed by exact numerical results, see later. From (22), we also find

$$\begin{aligned} r\approx \frac{48\gamma }{{\overline{N}}^2}+ \frac{64\gamma }{{\overline{N}}}\times O(\xi _1);\qquad n_s\approx 1-\frac{2}{{\overline{N}}}+{{\mathcal {O}}}(\xi _1) \end{aligned}$$

(25)

with ${\overline{N}}\approx N+9$ and $\gamma =1/4$ in the Weyl case and ${\overline{N}}\approx N+28$ and $\gamma =1$ for the Palatini case. Equations (25) are only an approximation and ignore some $\xi _1$ dependence in ${\overline{N}}$, but give an idea of the exact behaviour (see later, Fig. 2).

There is an additional constraint on the parameters space of Weyl/Palatini models, from the normalization of the CMB anisotropy $V_0/(24 \pi ^2 M^4 \epsilon _*)=\kappa _0$, $\kappa _0=2.1\times 10^{-9}$ and with $r<0.07$ [86] then $\xi _0=1/(\pi ^2 r \kappa ) \ge 6.89 \times 10^8$. With this bound, condition $\lambda _1 \xi _0 \ll \xi _1^2$ is respected for any perturbative $\xi _1$, $1/\xi _0$, by choosing an ultraweak $\lambda _1 \ll \xi _1^2/\xi _0$.

Let us compare Eq. (24) to that in the Starobinsky model of

$$\begin{aligned} {{\mathcal {L}}}= (-1/2) M^2\, R+ (\xi _0/4!)\, R^2, \end{aligned}$$

(26)

giving $V = V_0 \big (1-e^{-\varphi \sqrt{2/3}/M}\, \big )^2$ with $V_0 = 3 M^4/(2\xi _0)$; then $r \approx 12/N^2$, $n_s \approx 1 -2/N$ and

$$\begin{aligned} r= 3\, (1-n_s)^2. \end{aligned}$$

(27)

Interestingly, in Eq. (24) with $\xi _1 \sim 10^{-3}$ or smaller, the term $\propto \xi _1^2$ and higher powers have a negligible correction to r and $(1-n_s)^2$ and can be ignored; therefore Weyl inflation ($\gamma =1/4$) recovers relation (27) of Starobinsky model [32,33,34, 86]. For larger values of $\xi _1$ and fixed $n_s$, $\xi _1$ reduces r of Weyl inflation below that of Starobinsky model. In the Palatini case relation (27) is not possible (unless $\xi _1$ is tuned for every $n_s$) – the slope of $r(n_s)$ is different.

3.2 Numerical results

Our exact numerical results (with no expansion in powers of $\xi _1$) are given by the plots of potential, $(n_s,N)$, $(n_s,r)$, presented in Figs. 1 and 2 for Weyl and Palatini cases. Their differences are due to different $\gamma$. The results show a value of r smaller in the Weyl case than in Palatini case, for relevant $n_s$. For $n_s=0.9670\pm 0.0037\, (68\% \mathrm{CL})$ (TT, TE, EE + low E + lensing + BK14 +BAO) [86] one finds

$$\begin{aligned} \mathrm{Palatini:}&N=60,\quad 0.00794\le r\le 0.01002,\quad \end{aligned}$$

(28)

$$\begin{aligned} \mathrm{Weyl:}&N=60,\quad 0.00257\le r\le 0.00303. \end{aligned}$$

(29)

and for $n_s$ at $95\% \mathrm{CL}$ one has

$$\begin{aligned} \mathrm{Palatini:}&N=60,\quad 0.00700\le r\le 0.01002,\quad \end{aligned}$$

(30)

$$\begin{aligned} \mathrm{Weyl:}&N=60,\quad 0.00227\le r\le 0.00303. \end{aligned}$$

(31)

Fig. 2

The dependence $r(n_s)$ for various curves of constant N (as shown), for the Palatini theory ([P]) and Weyl theory ([W]). The dots stand for $\xi _1$ values corresponding to the curves in the last two plots in Fig. 1. The yellow (orange) area corresponds to the range measured for $n_s$ at $95 \%$CL $(68 \%)$, respectively. The curves show the largest range of values for r with $\lambda _1\xi _0\ll \xi _1^2$; this range shrinks towards smaller r if $\lambda _1\xi _0$ increases to $\lambda _1\xi _0\sim \xi _1^2$

The case of Starobinsky model for $N=60$ corresponds to the upper limit of r (0.003) of the Weyl model (top curve in Fig. 1 and highest r in Fig. 2 for $N=60$), while in the Palatini case a larger r is allowed for the same $n_s$, N.

While the plots in Fig. 1 have $\lambda _1\xi _0=10^{-8}$, they are actually more general. In the extreme case of $\lambda _1 \sim 0$, corresponding to a simplified potential (without the last term in (17)), the same range of values for $(n_s,r)$ shown in this figure remains valid. However, if we increase $\lambda _1\xi _0$ to $\lambda _1\xi _0 \approx \xi _1^2$, the last term in (17) becomes relatively large, the rightmost curves of V (of smallest $\xi _1$) have their minimum lifted and the range for $(n_s,r)$ in (28) to (31) is reduced: the smaller values $\xi _1 \sim 10^{-3}$ in Fig. 1, cannot then have successful inflation.

The main results of this work are summarised in Fig. 2; in this figure the dependence $r(n_s)$ is shown for different curves of constant N, that respect the required parametric constraint $\lambda _1\xi _0\le \xi _1^2$. The curves $r(n_s)$ give a numerically exact representation of the dependence in Eq. (24); they are extended even outside the $95\%$ CL range for $n_s$. In all cases, the Palatini case has r larger than in the Weyl case. This aspect and the different slope of the curves $r(n_s)$ can be used to distinguish these models from each other and from other models in future experiments.

The small r predicted by both Weyl and Palatini gravity models may be reached by the next generation of CMB experiments: CMB-S4, LiteBIRD, PICO, PIXIE [87,88,89,90,91,92], that will be sensitive to values as low as $r\sim 5\times 10^{-4}$. Therefore they will be able to test these two inflation models.

3.3 Corrections and other models

Compared to another model with Weyl gauge symmetry [29] (Fig. 2) which is linear in $R({\tilde{\Gamma }},g)$ and had $r\sim 0.04{-}0.06$, we see that the presence of the $R^2({\tilde{\Gamma }},g)$ term in the Weyl theory reduced r significantly (for a fixed $n_s$). Reducing r by an $R^2$ term also exists in the Palatini models without Weyl gauge symmetry [70]. Therefore, a small measured $r \sim 10^{-3}$ may indicate a preference for quadratic gravity models of inflation.

The Weyl inflation case of $\xi _1= 10^{-3}$ or smaller is similar to the Starobinsky model, with the difference that it needs an additional scalar field (the Higgs field¹³) to play the role of the inflaton. This is because the other scalar in the Weyl theory (radial direction $\rho$ in the $\phi _0$, $\phi _1$ space) is used to generate the Planck scale and the mass of $w_\mu$. Briefly, Weyl gravity gives a relation $r(n_s)$ similar to that in the Starobinsky model, with similar, large $\xi _0$, while also providing protection against corrections to r from higher dimensional operators; these are forbidden since their effective scale violates the symmetry; the Stueckelberg field cannot play the role of this scale since it was eaten by the Weyl field to all orders. Another benefit for Weyl inflation is the minimal approach: one only needs to consider the SM Higgs field in the Weyl conformal geometry; the underlying geometry provides the spontaneous breaking of the Weyl quadratic gravity action to the Einstein action and the Planck scale generation.

Despite this similarity of the Weyl and the Starobinsky models, it is possible to distinguish between them; it may happen that a curve $r(n_s)$ corresponding to $\xi _1>10^{-3}$ is preferred by data (see $r(n_s)$ curves in Fig. 1), in which case it is shifted below that of the Starobinsky model for the same $n_s$ – the two models are distinguishable. Also the Weyl model has an additional coupling, see $\Delta L$ in (19). While $\Delta L$ does not mix linear perturbations of $\delta w_\mu$ and of $\delta \varphi$, it can lead however to cubic interactions of the form $f'(\varphi ) \delta \varphi \delta w_\mu \delta w^\mu$. These can result in different predictions for the inflationary bispectrum compared to the pure single-field case. This can be used to further distinguish the Weyl case from the Starobinsky $R^2$ inflation (in case of $\xi _1\sim 10^{-3}$). The analysis of non-Gaussianities is thus interesting for further research.

The above results are subject to corrections from other operators of $d=4$ that may exist and are Weyl gauge invariant, as we discuss below.

In the Weyl case the Weyl-tensor-squared operator of Weyl geometry may be present $(1/\zeta ) {\tilde{C}}_{\mu \nu \rho \sigma }^2$. This can be re-written in a metric description as the Weyl-tensor-squared term of Riemannian geometry $(1/\zeta )\, C_{\mu \nu \rho \sigma }^2$ plus a gauge kinetic term of $w_\mu$ which gives a threshold correction to our coupling $\alpha$. The Weyl tensor term is invariant under Weyl gauge transformations performed to reach the Einstein-Proca action, hence one simply adds it to the final action, Eq. (14). This operator has an impact on the value of r that we found numerically and in Eq. (25) with $\gamma =1/4$ for Weyl case. The overall impact of the Weyl tensor term is essentially a rescaling of r into¹⁴$r_c=r\,(1+ 8/(\zeta \,\xi _0))^{1/2}$ [7]. Since our $\xi _0$ is large, only a low $\vert \zeta \vert \sim 1/\xi _0$ can increase r and this comes with an instability since the mass of the associated spin-two ghost (or tachyonic) state that this operator brings is $m^2\sim \zeta \, M^2$, where M is the Planck scale. Therefore, a stable Weyl gravity model up to the Planck scale will not modify the value of r. Other operators in Weyl gravity are topological and do not affect r (classically).

In the Palatini case one should consider the remaining quadratic operators of $d=4$ [93] that are Weyl gauge invariant and have a symmetric connection. They modify the equation of motion of ${\tilde{\Gamma }}$ and the vectorial non-metricity (B-6); unfortunately, it does not seem possible to find in this case an analytical solution to this equation due to its modified, complex structure and new states present (ghosts, etc). Additional simplifying assumptions would be needed, making the analysis model dependent. We only mention here the interesting possibility that for a symmetric ${\tilde{\Gamma }}$, the solution ${\tilde{\Gamma }}$ may become equal to that in Weyl-geometry (A-5); if so, the Palatini approach would provide an “offshell” version of Weyl quadratic gravity that is recovered for ${\tilde{\Gamma }}$ onshell.

4 Conclusions

We made a comparative study of the action and inflation in two theories of quadratic gravity with Weyl gauge symmetry: the original Weyl gravity action and the Palatini version of the same action, obtained by replacing the Weyl connection by Palatini connection. The actions of these theories are non-minimally coupled to a (Higgs-like) field $\phi _1$, necessary for inflation.

Given the symmetry, there is no scale in these theories. Mass scales are generated by an elegant spontaneous breaking of gauged scale symmetry that happens even in the absence of matter: the necessary scalar field (Stueckelberg field $\phi _0$) is not added ad-hoc as usually done to this purpose, but is of geometric origin and is ”extracted” from the $R({\tilde{\Gamma }},g)^2$ term in the action. If matter ($\phi _1$) is present, the Stueckelberg field is actually the radial direction ($\rho$) in the field space of $\phi _0$ and $\phi _1$; the field $\rho$ is then eaten by the Weyl gauge field $w_\mu$ which acquires mass $m_w\sim \langle \rho \rangle$ near the Planck scale. The breaking conserves the number of degrees of freedom and generates in the broken phase the Einstein-Proca action for $w_\mu$. In both theories, below the mass of $w_\mu$ the connection becomes Levi-Civita and Einstein gravity is recovered, with an “emergent” Planck scale $M\sim \langle \rho \rangle$ and a scalar potential (of the remaining angular-variable field).

The potential $V(\varphi )$ is controlled by the symmetry of the theory together with effects from the non-trivial connection ${\tilde{\Gamma }}$, different in the two theories. For small field values, V is similar in both theories; the scalar field can act as the Higgs field, in which case the potential displays electroweak symmetry breaking. For large field values, the potential has the same form in Weyl and Palatini theories up to couplings and field rescaling (due to different non-metricity) and gives successful inflation.

Our main results, comparing inflation predictions in the two theories and summarised in Fig. 2, showed how different non-metricity impacts on inflation predictions. In Weyl gravity the scalar-to-tensor ratio $0.00257 \le r \le 0.00303$, which is smaller than in Palatini case, $0.00794 \le r \le 0.01002$, for measured $n_s$ at 68$\%$ CL and $N=60$ e-folds. Similar results exist for $n_s$ at $95\%$CL or mildly different N, etc. Such values of r will be measured by new CMB experiments that can then test and distinguish Weyl and Palatini quadratic gravity.

There are similarities of inflation in Weyl and Palatini cases to Starobinsky inflation ($R+\xi _0 R^2$). In Weyl and Palatini theories one also has an $R^2$ term with a large $\xi _0$ that reduces r, but one needs in addition a non-minimally coupled scalar field ($\phi _1$) for inflation; this is because the other (radial) combination enabled the breaking of gauged scale symmetry and the generation of mass scales (Planck, $w_\mu$ mass). In both Weyl and Palatini theory, for a fixed $n_s$, reducing the non-minimal coupling ($\xi _1$) increases r which in Weyl theory is bounded from above by that of Starobinsky inflation. Unlike in the Palatini theory, Weyl gravity for $\xi _1\le 10^{-3}$ gives a dependence $r(n_s)$ essentially similar to that in Starobinsky inflation, while also protecting r against higher dimensional operators corrections.

Appendix

1.1 A Weyl gravity

We include here basic information on Weyl gravity used in the text. First, in the (pseudo)-Riemannian case (Einstein gravity) $\nabla _\mu g_{\alpha \beta } = 0$ with $\nabla _\mu$ defined by the Levi-Civita connection

$$\begin{aligned} \Gamma _{\mu \nu }^\rho (g)= (1/2)\, g^{\rho \beta }\,(\partial _\nu g_{\beta \mu }+\partial _\mu g_{\beta \nu }-\partial _\beta g_{\mu \nu }). \end{aligned}$$

(A-1)

Setting $\nu =\rho$ and summing over gives $\Gamma _\mu \equiv \Gamma _{\mu \nu }^\nu =\partial _\mu \ln \sqrt{g}$ used in the text.

In Weyl gravity and conformal geometry the theory has vectorial non-metricity, i.e.

$$\begin{aligned} {\tilde{\nabla }}_\lambda \, g_{\mu \nu }=-w_\lambda \, g_{\mu \nu }, \end{aligned}$$

(A-2)

so $w_\lambda =(-1/4)\, g^{\mu \nu }\,{\tilde{\nabla }}_\lambda g_{\mu \nu }$; here ${\tilde{\nabla }}_\mu$ is defined by the Weyl connection ${\tilde{\Gamma }}_{\mu \nu }^\rho$:

$$\begin{aligned} {\tilde{\nabla }}_\lambda g_{\mu \nu }= \partial _\lambda g_{\mu \nu } - {\tilde{\Gamma }}_{\mu \lambda }^\rho g_{\rho \nu }-{\tilde{\Gamma }}_{\nu \lambda }^\rho g_{\mu \rho }. \end{aligned}$$

(A-3)

Write this for cyclic permutations of the indices and combine the three equations to find

$$\begin{aligned} {\tilde{\Gamma }}_{\mu \nu }^\rho =\Gamma _{\mu \nu }^\rho (g)+ (1/2)\, g^{\rho \lambda }\,({\tilde{\nabla }}_\lambda g_{\mu \nu }-{\tilde{\nabla }}_\mu g_{\nu \lambda } - {\tilde{\nabla }}_\nu g_{\lambda \mu }),\nonumber \\ \end{aligned}$$

(A-4)

which with (A-2) gives the Weyl connection

$$\begin{aligned} {\tilde{\Gamma }}_{\mu \nu }^\rho = \Gamma _{\mu \nu }^\rho (g)+(1/2)\,\big [\delta _\mu ^\rho \,w_\nu +\delta _\nu ^\rho \,w_\mu -g_{\mu \nu }\,w^\rho \big ]. \end{aligned}$$

(A-5)

${\tilde{\Gamma }}_{\mu \nu }^\rho$ are symmetric (${\tilde{\Gamma }}_{\mu \nu }^\rho ={\tilde{\Gamma }}_{\nu \mu }^\rho$) i.e. there is no torsion. ${\tilde{\Gamma }}$ is invariant under transformations (2), (3) since the variation of the metric is compensated by that of $w_\mu$. Using that $g^{\alpha \beta }{\tilde{\nabla }}_\lambda g_{\alpha \beta }=2{\tilde{\nabla }}_\lambda \ln \sqrt{g}$ one finds for the Weyl field

$$\begin{aligned} w_\lambda =(-1/2)\,\,{\tilde{\nabla }}_\lambda \ln \sqrt{g}. \end{aligned}$$

(A-6)

Setting $\nu =\rho$ in (A-5) and summing over, we recover our definition (3) in the text:

$$\begin{aligned} {\tilde{\Gamma }}_\mu =\Gamma _\mu (g)+2\, w_\mu . \end{aligned}$$

(A-7)

The Riemann and Ricci tensors in Weyl geometry are defined as in Riemannian geometry but with the replacement of the Levi-Civita connection $\Gamma _{\mu \nu }^\rho (g)$ by the new ${\tilde{\Gamma }}_{\mu \nu }^\rho$

$$\begin{aligned} R^\lambda _{\,\mu \nu \sigma }({\tilde{\Gamma }},g)= \partial _\nu {\tilde{\Gamma }}^\lambda _{\mu \sigma } -\partial _\sigma {\tilde{\Gamma }}^\lambda _{\mu \nu } + {\tilde{\Gamma }}^\lambda _{\nu \rho }\,{\tilde{\Gamma }}^\rho _{\mu \sigma } -{\tilde{\Gamma }}^\lambda _{\sigma \rho }\,{\tilde{\Gamma }}^\rho _{\mu \nu }, \end{aligned}$$

(A-8)

and

$$\begin{aligned} R_{\mu \sigma }({\tilde{\Gamma }},g)=R^\lambda _{\,\,\mu \lambda \sigma }({\tilde{\Gamma }},g),\qquad R({\tilde{\Gamma }},g)=g^{\mu \sigma }\,{{\tilde{R}}}_{\mu \sigma }({\tilde{\Gamma }},g). \end{aligned}$$

(A-9)

Since ${\tilde{\Gamma }}$ is invariant under transformations (2), (3), then the Riemann and Ricci tensors of Weyl geometry are also invariant. Since the Weyl scalar curvature $R({\tilde{\Gamma }},g)$ contains $g^{\mu \nu }$, it transforms covariantly

$$\begin{aligned} \hat{R}({\tilde{\Gamma }},g)= (1/\Omega ^2)\,R({\tilde{\Gamma }},g). \end{aligned}$$

(A-10)

This helps build Weyl gauge invariant operators. Using the expression of ${\tilde{\Gamma }}$, one shows

$$\begin{aligned} R({\tilde{\Gamma }},g) = R(g) - 3 \, \nabla _\mu w^\mu -\frac{3}{2} \, g^{\mu \nu }\,w_\mu w_\nu , \end{aligned}$$

(A-11)

where R(g) is the Riemannian scalar curvature and $\nabla _\mu w^\mu$ is defined by Levi–Civita connection. Equation (A-11) was used in the text, in going from (10) to (12) for the Weyl case.

1.2 B Palatini gravity

We present here the connection and the scalar curvature for the Palatini approach to gravity, used in the text. In this case, similarly to Weyl gravity, ${\tilde{\Gamma }}$ is not determined by the metric (apriori is independent of it), hence it is invariant under rescaling $g_{\mu \nu }$. The connection is determined by its equation of motion from the Lagrangian of Eq. (10). Solving this equation of motion one finds [8, (Eqs. 23, 25, 39)]

$$\begin{aligned} {\tilde{\nabla }}_\lambda (\rho ^2 g_{\mu \nu }) =(-2)\rho ^2 (g_{\mu \nu }\,V_\lambda -g_{\mu \lambda } V_\nu - g_{\nu \lambda } V_\mu ), \end{aligned}$$

(B-1)

where $V_\lambda$ is some arbitrary vector, related to $w_\lambda$ (see below). One writes (B-1) for cyclic permutations of the three indices, then combines the equations obtained and uses the symmetry ${\tilde{\Gamma }}_{\mu \nu }^\alpha ={\tilde{\Gamma }}_{\nu \mu }^\alpha$, to find

$$\begin{aligned} {\tilde{\Gamma }}_{\mu \nu }^\alpha= & {} \Gamma _{\mu \nu }^\alpha (\rho ^2 g) -\,\big (3\, g_{\mu \nu }\, V_\lambda -g_{\nu \lambda }\,V_\mu - g_{\lambda \mu } \,V_\nu \,\big )\,g^{\lambda \alpha }, \end{aligned}$$

(B-2)

where

$$\begin{aligned} \Gamma ^\alpha _{\mu \nu }(\rho ^2 g)=\Gamma ^\alpha _{\mu \nu }(g)+1/2\, \big ( \delta _\nu ^\alpha \, \partial _\mu +\delta _\mu ^\alpha \, \partial _\nu -g^{\alpha \lambda } g_{\mu \nu } \,\partial _\lambda ) \ln \rho ^2, \end{aligned}$$

(B-3)

with $\Gamma _{\mu \nu }^\alpha (g)$ the Levi-Civita connection for $g_{\mu \nu }$. Setting $\nu = \alpha$ in (B-2) one then finds ${\tilde{\Gamma }}_\mu =\Gamma _\mu (\phi ^2 g)+ 2\, V_\mu$ and from (B-3): $\Gamma _\mu (\phi ^2 g)=\Gamma _\mu (g)+2 \,(\partial _\mu \ln \rho ^2)$. From these two equations and with the definition $w_\lambda = 1/2\, ({\tilde{\Gamma }}_\mu -\Gamma _\mu (g))$, then $V_\lambda =w_\lambda -\partial _\lambda \ln \rho ^2$. Using this relation and that found by contracting (B-1) by $g^{\mu \nu }$, then

$$\begin{aligned} w_\lambda =(-1/2) {\tilde{\nabla }}_\lambda \ln \sqrt{g}. \end{aligned}$$

(B-4)

similar to (A-6), but with different ${\tilde{\Gamma }}$. Finally, Eqs. (B-2), (B-3) together with $V_\lambda =w_\lambda -\partial _\lambda \ln \rho ^2$, give the expression of ${\tilde{\Gamma }}$ in terms of $g_{\mu \nu }$, $\rho$ and $w_\lambda$ and verifies that ${\tilde{\Gamma }}$ is indeed invariant under a gauged scale transformation (2), (3). This is obvious since $\rho ^2 g_{\mu \nu }$ and $V_\mu$ are invariant in (B-2). With ${\tilde{\Gamma }}$ a function of $w_\lambda$, $\phi$, $g_{\mu \nu }$, one computes the Ricci tensor $R_{\mu \nu }({\tilde{\Gamma }})$ for Palatini gravity, then the scalar curvature $R({\tilde{\Gamma }},g)=g^{\mu \nu } R_{\mu \nu } ({\tilde{\Gamma }},g)$. The result is [8]:

$$\begin{aligned} R({\tilde{\Gamma }},g)= & {} R(g)-6 g^{\mu \nu } \nabla _\mu \nabla _\nu \ln \rho -6 (\nabla _\mu \ln \rho )^2 \nonumber \\&-12\, \big (\nabla _\lambda V^\lambda + V^\lambda \partial _\lambda \ln \rho ^{{2}}\big ) -6 V_\mu \, V^\mu , \end{aligned}$$

(B-5)

with R(g) the Ricci scalar (Riemannian case), and $V_\lambda \equiv w_\lambda -\partial _\lambda \ln \rho ^2$. Replacing (B-5) in Eq. (10) for the Palatini case, one finds after some algebra Eq. (12) in the text with $\gamma =1$. At the same time, the vectorial non-metricity becomes

$$\begin{aligned} {\tilde{\nabla }}_\lambda g_{\mu \nu }=(-2)\,(g_{\mu \nu } w_\lambda -g_{\mu \lambda } w_\nu -g_{\nu \lambda } w_\mu ), \end{aligned}$$

(B-6)

which is different from (A-2) of Weyl geometry, but has the same trace $g^{\mu \nu }{\tilde{\nabla }}_\lambda g_{\mu \nu }=-w_\lambda /4$.

1.3 C Inflation: perturbations to the scalar and vector fields

We discuss in detail the scalar ($\delta \phi$) and vector ($\delta w_\mu$) fields perturbations in a FRW universe $g_{\mu \nu } = (1, -a(t)^2, -a(t)^2, -a(t)^2)$ and show that $\Delta L$ of (19) does not affect inflation by $\varphi$. To simplify notation hereafter we remove the ’hat’ (${}^{\wedge }$) on $w_\mu$, $g_{\mu \nu }$ when we refer to action (16).

$\bullet$ Let us first review the usual case of a single scalar field, see e.g. [84], needed later. Consider

$$\begin{aligned} {{\mathcal {L}}}_\varphi =\int \sqrt{g} \Big [\frac{1}{2} \,g^{\mu \nu } \,\partial _\mu \varphi \partial _\nu \varphi -\mathcal {V}(\varphi )\Big ]. \end{aligned}$$

(C-1)

The equation of motion $\nabla _\mu \nabla ^\mu \varphi + \mathcal {V}^\prime (\varphi )=0$ gives for a FRW metric:

$$\begin{aligned} \ddot{\varphi }(\vec x,t)+ 3 H {\dot{\varphi }}(\vec x,t)-\frac{1}{a(t)^2} \partial _j\partial _j \varphi (\vec x,t)+{{\mathcal {V}}}^\prime (\varphi )=0\nonumber \\ \end{aligned}$$

(C-2)

Expanding about $\varphi (t)$, with $\varphi (\vec x,t)=\varphi (t)+\delta \varphi (\vec x,t)$, one has at linear level

$$\begin{aligned}&\delta \ddot{\varphi }(\vec x,t)+ 3 H \delta {\dot{\varphi }}(\vec x,t) \nonumber \\&\quad -\frac{1}{a(t)^2} \partial _j\partial _j \delta \varphi (\vec x,t)+{{\mathcal {V}}}''(\varphi (t))\delta \varphi (\vec x,t)=0 \end{aligned}$$

(C-3)

Using mode expansion $\delta \varphi (\vec x,t)=\int d^3k/(2\pi )^{3/2} \delta \varphi _k(t) \exp ( i \vec x \vec k)$, then

$$\begin{aligned} \delta \ddot{\varphi }_k+ 3 H \delta {\dot{\varphi }}_k+ \big [ k^2/a^2+{{\mathcal {V}}}''(\varphi (t))\big ] \delta \varphi _k=0 \end{aligned}$$

(C-4)

or, with a notation $\delta \phi _k=\delta \chi _k/a(t)$

$$\begin{aligned} \delta \ddot{\chi }_k+ H \delta {\dot{\chi }}_k+ \big [ k^2/a^2-\dot{H} -2 H^2+{{\mathcal {V}}}''(\varphi (t))\big ] \delta \varphi _k=0. \end{aligned}$$

(C-5)

In conformal time ($\eta$) via $dt=a(t)^2 d\eta$, this equation becomes

$$\begin{aligned} \delta \chi ''_k+ \big [ k^2 -(1/\eta ^2)\, (\nu ^2-1/4)\big ] \delta \varphi _k=0, \quad \nu ^2=9/4-{{\mathcal {V}}}''/H^2. \end{aligned}$$

(C-6)

where we used that with $a\sim e^{H t}$ then $a(\eta )=-1/(H\eta )$ and $2/\eta ^2=a''/a$ with $H\sim$constant. In the subhorizon limit $-\eta \, k\gg 1$ the solution should be $\delta \chi _k=e^{-i k \eta }/\sqrt{2 k}$. With this boundary condition, the solution is

$$\begin{aligned} \delta \chi _k=\frac{\sqrt{\pi }}{2} e^{i (\nu +1/2) \pi /2}\sqrt{-\eta }\,H_\nu ^{(1)}(-\eta k) \end{aligned}$$

(C-7)

where $H^{(1)}$ is the Hankel function of first kind. This leads to the usual power spectrum, with

$$\begin{aligned}&\vert \delta \phi _k\vert ^2\approx \frac{H^2}{2 k^3}\Big (\frac{k}{a H}\Big )^{2\eta _\phi }, \qquad \nonumber \\&\quad P_{\delta \phi _k} =\frac{k^3}{2\pi ^2} \vert \delta \phi _k\vert ^2=\Big (\frac{H}{2\pi }\Big )^2\,\Big (\frac{k}{a H}\Big )^{2\eta _\phi } \end{aligned}$$

(C-8)

with $\eta _\phi =3/2-\nu \approx {{\mathcal {V}}}''/(3 H^2)=M_p^2\,{{\mathcal {V}}}''/{{\mathcal {V}}}\ll 1$. This gives $n_\phi =1+2\eta _\phi$ ($H\sim$ constant).

For later use, we also consider solution (C-7) when ${{\mathcal {V}}}''(\varphi ) > (9/4)\, H^2$ i.e. $\nu$ is imaginary, $\nu =i{\tilde{\nu }}$, ${\tilde{\nu }}$ real. In the (superhorizon) limit $(-\eta \, k)\ll 1$ one finds:

$$\begin{aligned} \delta \chi _k= & {} \frac{(1+i)\, 2^{-3/2-i{\tilde{\nu }}} e^{-{\tilde{\nu }}\pi /2}}{\sqrt{\pi k} \Gamma (1+i {\tilde{\nu }})} \nonumber \\&\times \Big [\pi (-\eta k)^{2 i {\tilde{\nu }}} (1+\coth \pi {\tilde{\nu }})+2^{2i{\tilde{\nu }}} {\tilde{\nu }}\, \Gamma (i{\tilde{\nu }})^2\Big ]. \end{aligned}$$

(C-9)

Returning to $\delta \phi _k$ notation, one finds (see e.g. [84])

$$\begin{aligned} P_{\delta \phi _k} =\frac{\pi e^{-\pi {\tilde{\nu }}}}{2} \frac{H^2}{(2\pi )^2} \Big (\frac{k}{a H}\Big )^3\,\{....\} \end{aligned}$$

(C-10)

where the brackets $\{...\}$ stand for terms that vanish when ${\tilde{\nu }}\rightarrow \infty$ (${{\mathcal {V}}}''(\varphi )\gg H^2$). Therefore, modes $\delta \phi _k$ of $\nu$ imaginary are exponentially suppressed [85]; this is expected since they are too massive to be excited.

$\bullet$ Consider now our action (16); its $\varphi$-dependence is described by ${{\mathcal {L}}}_\varphi$ by replacing in (C-1)

$$\begin{aligned} {{\mathcal {V}}}(\varphi )\rightarrow {{\mathcal {V}}}(\varphi ,w)=V(\varphi )-\frac{1}{2} f(\varphi )w_\mu w^\mu \end{aligned}$$

(C-11)

with $V(\varphi )$ of Eq. (17) and $f(\varphi )$ of Eq. (19). In this case (C-2) and the equation for $\varphi (t)$ receive a correction from the last term in the rhs of (C-11). Then Eq. (C-4) for the perturbations $\delta \varphi _k$, also with $w_\mu (\vec x,t)=w_\mu (t)+\delta w_\mu (\vec x,t)$, is now modified into

$$\begin{aligned}&\delta \ddot{\varphi }_k+ 3 H \delta {\dot{\varphi }}_k+ \big [ k^2/a^2+{{\mathcal {V}}}''(\varphi (t),w(t))\big ] \delta \varphi _k \nonumber \\&\quad =f^\prime (\varphi (t)) w_\mu (t) \delta w^\mu (\vec k,t), \end{aligned}$$

(C-12)

where the second derivative ${{\mathcal {V}}}''$ is with respect to $\varphi$ and $\delta w_\mu (\vec k,t)$ are the Fourier modes of $\delta w_\mu (\vec x,t)=\int d^3k/(2\pi )^{3/2} \delta w_\mu (\vec k, t) \exp (i\vec k \vec x)$. Next, the background $w_\mu (t)$ compatible with the FRW metric is $w_\mu (t) = (w_0(t),0,0,0)$, while from (16), the equation of motion of $w_\mu$ gives

$$\begin{aligned} \frac{1}{\sqrt{g}}\,\partial _\rho \, \big [\sqrt{g}\, F^{\rho \mu }\,\big ] + f(\varphi )\, w^\mu =0. \end{aligned}$$

(C-13)

One has a trivial solution $w_\mu (t) = 0$ ($f(\varphi ) \ne 0$). Therefore, in (C-12) we must replace ${{\mathcal {V}}}''(\varphi (t),w(t)) \rightarrow {{\mathcal {V}}}''(\varphi (t),0)= V''(\varphi )$ while the rhs of (C-12) is vanishing. Therefore equation (C-12) of $\delta \phi _k$ is actually independent of $w_\mu$ and $\delta w_\mu$ and there is no mixing of $\delta \varphi$ to $\delta w_\mu$¹⁵. Then the calculation of $\delta \varphi _k$ proceeds as earlier but for potential $V(\varphi )$, see (C-8) for ${{\mathcal {V}}}(\varphi ) \rightarrow V(\varphi )$. Thus $\Delta L$ does not impact on $\varphi$-inflation and the usual formulae of single-field inflation in Einstein gravity apply, as used in Sect. 3.1.

$\bullet$ We saw above that the perturbations $\delta \varphi$ do not mix with those of $w_\mu$ and $\varphi$-inflation decouples from $w_\mu$ in a FRW universe. While somewhat beyond the purpose of this work, we also examine below the vector field perturbations, following [82, 83], in the approximation $H\sim$ constant. Compatibility with the FRW metric demands computing the perturbations about a background $w_\mu (t)=0$ as seen earlier. In fact we may take a more general background, if initially the vector field contribution to the stress-energy tensor is negligible relative to that of the scalar, in an isotropic universe; we shall then consider a quasi-homogeneous field $\partial _i w^\alpha =0$. Our FRW case is always restored by setting anywhere below $w_\mu (t)=0$. Then from (C-13) for $\mu =0$ and $\mu =i$, respectively

$$\begin{aligned} w_0(t)=0 \quad \text {and}\quad \ddot{w}_i(t)+ H {\dot{w}}_i(t) + f(\varphi ) \,w_i(t)=0. \end{aligned}$$

(C-14)

In an expanding FRW universe the relevant physical quantity is not $w_i$ ($i=1,2,3$) but $q_i=w_i/a$, as also seen from the norm $w_\mu w^\mu =w_0^2-(w_i w_i)/a^2$ (sum over i) and from the stress energy tensor [81, 82]. Then the last equation becomes

$$\begin{aligned} \ddot{q}_i+ 3 H \dot{q}_i+ (2 H^2+ f(\varphi ))\, q_i=0. \end{aligned}$$

(C-15)

Denote $m^2=2 H^2+f(\varphi (t))$ where $f(\varphi )>0$ since $f(\varphi (t))=6\gamma M^2\{1+\sinh ^2[\varphi (t)/(2 M\sqrt{\gamma })]\}$, Eq. (19). Ignoring the time dependent part in $f(\varphi )$, the solution is

$$\begin{aligned}&q_i(t)\propto 1/a(t)^{3/2} (c_1\, e^{- \alpha t/2} +c_2\, e^{\alpha t/2}), \qquad \nonumber \\&\quad \alpha = \sqrt{H^2-4 m^2}. \end{aligned}$$

(C-16)

with constants $c_{1,2}$. Since $\alpha$ is purely imaginary, during inflation the vector field is massive with damped oscillations (up to corrections due to $\varphi (t))$). Its contribution to the stress energy tensor ($T^\mu _\nu$) is anisotropic; the spatial part of this tensor contains off-diagonal entries of comparable size to the diagonal ones and can be made diagonal for a particular direction of the vector field. However, with $q_i(t)\sim 1/a(t)^{3/2}$, the contribution of the vector field to $T^\mu _\nu$ during inflation is suppressed by the scale factor $1/a(t)^3$ relative to that of¹⁶$\varphi$.

Consider now the equations for perturbations, with $w_\mu (\vec x, t)=w_\mu (t)+\delta w_\mu (\vec x,t)$. Then Eq. (C-13) for $\mu =i$ and $\mu =0$ give

$$\begin{aligned}&\ddot{w}_i+ H\,{\dot{w}}_i -\frac{1}{a(t)^2} \big [\partial _j\partial _j w_i- \partial _i \partial _jw_j\big ] +f(\varphi )\, w_i \nonumber \\&\quad = \partial _i{\dot{w}}_0 +H \partial _i w_0 \end{aligned}$$

(C-18)

$$\begin{aligned}&\partial _i{\dot{w}}_i -\partial _i \partial _iw_0 +a(t)^2 \,f(\varphi ) w_0 = 0 \end{aligned}$$

(C-19)

with $w_\mu =w_\mu (\vec x,t)$ and $\varphi =\varphi (\vec x,t)$. By applying $\partial _\mu$ on (C-13) we find

$$\begin{aligned} i \partial _i {\dot{w}}_0 -\frac{1}{a(t)^2} \partial _i\partial _j w_j+ 3 H \partial _i w_0+\partial _i D=0 \end{aligned}$$

(C-20)

where $D = D(\vec x,t)$ and $D = w_0\partial _0\ln f(\varphi )-1/a(t)^2 w_j \partial _j \ln f(\varphi )$. Adding (C-18), (C-20) then

$$\begin{aligned} \ddot{w}_i + H {\dot{w}}_i -\frac{1}{a(t)^2} \partial _j\partial _j w_i + f(\varphi ) w_i = -2 H \partial _i w_0 -\partial _i D. \end{aligned}$$

(C-21)

This gives for perturbations $\delta w_\mu$ a linear differential equation:

$$\begin{aligned}&\delta \ddot{w}_i + H \delta {\dot{w}}_i -\frac{1}{a(t)^2} \partial _j\partial _j \delta w_i + f(\varphi (t)) \delta w_i \nonumber \\&\quad = -(2 H+\partial _0\ln f(\varphi (t))) \partial _i \delta w_0 \nonumber \\&\qquad - f^\prime (\varphi (t)) w_j(t) \sigma _{ij}(t) \end{aligned}$$

(C-22)

Here $\sigma _{ij}(\vec x,t)= [\delta _{ij}+ 1/(a(t)^2 f(\varphi (t)))\,\, \partial _i\partial _j]\, \delta \varphi (\vec x,t)$; notice that in general case of $w_i(t) \ne 0$ (C-22) is “mixing” $\delta \varphi$ and $\delta w_\mu$. However, this mixing is absent in our FRW case of $w_\mu (t) = 0$.

Further, from remaining (C-19)

$$\begin{aligned}&\partial _i\, \delta {\dot{w}}_i(\vec x,t)-\partial _i\partial _i\,\delta w_0(\vec x,t) \nonumber \\&\quad +a(t)^2\, f(\varphi (t))\,\delta w_0(\vec x,t)=0. \end{aligned}$$

(C-23)

or, in Fourier modes

$$\begin{aligned} \delta w_0(\vec k, t)=-i\frac{k_j \delta {\dot{w}}_j (\vec k, t)}{k^2+a^2 f(\varphi (t))}. \end{aligned}$$

(C-24)

We separate the perturbations into parallel and orthogonal directions to $\vec k$ (taken along OZ):

$$\begin{aligned} \delta \vec w^\parallel =\frac{\vec k (k_i \delta w_i)}{k^2}, \qquad \delta \vec w^\perp =\delta \vec w-\delta \vec w^\parallel . \end{aligned}$$

(C-25)

We introduce the physical perturbations $\delta q_\mu (\vec x,t)=(1/a(t))\,\delta w_\mu (\vec x,t)$ and express (C-22) in terms of the Fourier modes $\delta q_\mu (\vec k,t)$ defined by $\delta q_\mu (\vec x,t)=\int d^3k/(2\pi )^{3/2} \delta q_\mu (k,t) \exp (i\vec k\vec x)$. We find for the Fourier modes of parallel $\delta q_z^\parallel (\vec k,t)$ and orthogonal $\delta q^\perp _j(\vec k,t)$ directions¹⁷

$$\begin{aligned}&\delta \ddot{q}^{\parallel }_z+\delta \dot{q}_z^\parallel \, \Big [ 3H+ \theta _1\Big ] \nonumber \\&\quad +\Big [\,\frac{k^2}{a^2}+2 H^2+ H \theta _1+ f(\varphi (t)) \Big ]\delta q_z^\parallel =\theta _2, \end{aligned}$$

(C-26)

$$\begin{aligned}&\delta \ddot{q}_j^\perp + 3 H\,\delta \dot{q}_j^\perp \nonumber \\&\quad +\Big [\,\frac{k^2}{a^2}+2H^2+ f(\varphi (t))\,\Big ]\delta q_j^\perp = 0, \quad j=1,2. \end{aligned}$$

(C-27)

where

$$\begin{aligned}&\theta _1=\frac{k^2 \big ( 2 H+\partial _0 \ln f(\varphi (t)))}{k^2+a^2 f(\varphi (t)\big )}, \qquad \nonumber \\&\theta _2=-\delta \varphi _k\, q_z(t) f^\prime (\varphi (t)) \Big (1- \frac{k^2}{a^2 f(\varphi (t))}\Big ). \end{aligned}$$

(C-28)

Equations (C-26), (C-27) are similar to those in [82, Eqs. 21, 22, 67] except an extra $\varphi$-dependent correction to the mass ($\sim M^2$) of $w_\mu$ that induces $\theta _2$ and a time derivative in $\theta _1$.

Equation (C-27) is similar to that for the scalar field perturbations, Eq. (C-4). We expect perturbations $\delta q_j^\perp$ be generated if their effective mass $m^2=2 H^2+f(\varphi (t))<H^2$. This condition is not respected since $f(\varphi )>0$. The power spectrum is exponentially suppressed, as for the scalar field, Eq. (C-4) with ${{\mathcal {V}}}'' \rightarrow f(\varphi (t))+2H^2$ with $\nu$ imaginary and Eq. (C-10).

Similar considerations apply to the perturbations to the parallel (longitudinal) mode of $w_\mu$. For our FRW-compatible background $q_z^\parallel (t)=0$ ($w_\mu (t)=0$), hence $\theta _2=0$. Therefore, there is no mixing of $\delta q_z^\parallel$ and $\delta \varphi _k$ perturbations in (C-26), in agreement with the earlier similar finding, see discussion around Eq. (C-12). Note also that if $k^2\ll a^2 f(\varphi )$, $\delta q_z^\parallel$ has an equation similar to the transverse modes, with $\theta _1\sim 0$ (with $H\sim$constant, ${\dot{\varphi }}^2\sim -2 \dot{H}^2 M^2$). Similar to the transverse case, the effective mass $m^2=2H^2+ H \theta _1 +f(\varphi (t))$ of $\delta q_z^\parallel$ is again larger than H and its generation is exponentially suppressed. We see again that in the FRW case one can ignore the effect of $\delta w_\mu$ and of coupling of $w_\mu -\varphi$ on $\delta \phi _k$.

In a general background case $q_z^\parallel (t) \ne 0$, then $\theta _2 \ne 0$; then a mixing of perturbations of $\varphi$ and of longitudinal mode of $w_\mu$ exists in (C-26) due to coupling $f(\varphi ) w_\mu w^\mu$, Eq. (19). However, even in this case, $q_z^\parallel$ is suppressed by the scale factor, due to Eq. (C-16), and thus the same is true for the mixing.