Skip to main content
SpringerLink
Log in

New numerical approximation of fractional derivative with non-local and non-singular kernel: Application to chaotic models

  • Regular Article
  • Published:
The European Physical Journal Plus Aims and scope Submit manuscript

An Author Correction to this article was published on 01 February 2022

This article has been updated

Abstract.

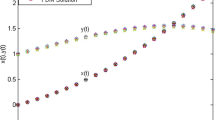
Recently a new concept of fractional differentiation with non-local and non-singular kernel was introduced in order to extend the limitations of the conventional Riemann-Liouville and Caputo fractional derivatives. A new numerical scheme has been developed, in this paper, for the newly established fractional differentiation. We present in general the error analysis. The new numerical scheme was applied to solve linear and non-linear fractional differential equations. We do not need a predictor-corrector to have an efficient algorithm, in this method. The comparison of approximate and exact solutions leaves no doubt believing that, the new numerical scheme is very efficient and converges toward exact solution very rapidly.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Change history

References

  1. Jürg Nievergelt, Commun. ACM. 7, 731 (1964)

    Article  Google Scholar 

  2. Markus Kunze, Tassilo Kupper, Non-smooth dynamical systems: An overview, in Ergodic Theory, Analysis, and Efficient Simulation of Dynamical Systems, edited by Bernold Fiedler (Springer Science & Business Media, 2001) p. 431

  3. Thao Dang, Model-Based Testing of Hybrid Systems, in Model-Based Testing for Embedded Systems, edited by Justyna Zander, Ina Schieferdecker, Pieter J. Mosterman (CRC Press, 2011) p. 411

  4. Ernst Hairer, Syvert Paul Nørsett, Gerhard Wanner, Solving ordinary differential equations I: Nonstiff problems, second edition (Springer Verlag, Berlin, 1993)

  5. John Denholm Lambert, Numerical Methods for Ordinary Differential Systems (John Wiley & Sons, Chichester, 1991)

  6. W. Kahan, A survey of error-analysis, in Proceedings of IFIP Congress 71, edited by C.V. Freiman, John E. Griffith, J.L. Rosenfeld (North-Holland, Amsterdam, 1972) pp. 1214--1239

  7. Michele Caputo, Geophys. J. Int. 13, 529 (1967)

    Article  Google Scholar 

  8. Obaid Jefain Julaighim Algahtani, Chaos, Solitons Fractals 89, 552 (2016)

    Article  MathSciNet  Google Scholar 

  9. Badr Saad T. Alkahtani, Chaos, Solitons Fractals 89, 547 (2016)

    Article  ADS  Google Scholar 

  10. A. Atangana, B. Dumitru, Therm. Sci. 20, 763 (2016)

    Article  Google Scholar 

  11. A. Atangana, I. Koca, Chaos, Solitons Fractals 89, 447 (2016)

    Article  ADS  MathSciNet  Google Scholar 

  12. G.G. Dahlquist, BIT Numer. Math. 3, 27 (1963)

    Article  Google Scholar 

  13. W.E. Milne, Numerical integration of ordinary differential equations, in American Mathematical Monthly, Mathematical Association of America, Vol. 33 (1926) pp. 455--460

  14. Germund Dahlquist, Math. Scandin. 4, 33 (1956)

    Article  Google Scholar 

  15. Florian A. Potra, Stephen J. Wright, J. Comput. Appl. Math. 124, 281 (2000)

    Article  ADS  MathSciNet  Google Scholar 

  16. Wimol San-Um, Banlue Srisuchinwong, J. Comput. 7, 1041 (2012)

    Google Scholar 

  17. Tao Yang, Leon O. Chua, J. Bifurc. Chaos 10, 2015 (2015)

    Article  Google Scholar 

  18. V. Carmona, E. Freire, E. Ponce, F. Torres, IEEE Trans. Circ. Syst. I 49, 609 (2002)

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Applied Mathematics, Faculty of Science, Université Moulay Ismail, B.P. 11201, Zitoune Meknès, Morocco

    Mekkaoui Toufik

  2. Institute for groundwater studied, Faculty of Natural and Agricultural Science, University of Free State, 9300, Bloemfontein, South Africa

    Abdon Atangana

Authors
  1. Mekkaoui Toufik
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Abdon Atangana
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Abdon Atangana.

Additional information

The original online version of this article was revised to correct equation 14.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Toufik, M., Atangana, A. New numerical approximation of fractional derivative with non-local and non-singular kernel: Application to chaotic models. Eur. Phys. J. Plus 132, 444 (2017). https://doi.org/10.1140/epjp/i2017-11717-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1140/epjp/i2017-11717-0

Search

Navigation