Impact of control interventions on COVID-19 population dynamics in Malaysia: a mathematical study

Abstract

Coronavirus disease 2019 (COVID-19) pandemic has posed a serious threat to both the human health and economy of the affected nations. Despite several control efforts invested in breaking the transmission chain of the disease, there is a rise in the number of reported infected and death cases around the world. Hence, there is the need for a mathematical model that can reliably describe the real nature of the transmission behaviour and control of the disease. This study presents an appropriately developed deterministic compartmental model to investigate the effect of different pharmaceutical (treatment therapies) and non-pharmaceutical (particularly, human personal protection and contact tracing and testing on the exposed individuals) control measures on COVID-19 population dynamics in Malaysia. The data from daily reported cases of COVID-19 between 3 March and 31 December 2020 are used to parameterize the model. The basic reproduction number of the model is estimated. Numerical simulations are carried out to demonstrate the effect of various control combination strategies involving the use of personal protection, contact tracing and testing, and treatment control measures on the disease spread. Numerical simulations reveal that the implementation of each strategy analysed can significantly reduce COVID-19 incidence and prevalence in the population. However, the results of effectiveness analysis suggest that a strategy that combines both the pharmaceutical and non-pharmaceutical control measures averts the highest number of infections in the population.

1 Introduction

In December 2019, a novel strand of coronavirus, namely severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2), causing coronavirus disease 2019 (COVID-19) emerged in Wuhan, Hubei Province of China [1,2,3]. The Chinese government reported the virus to the World Health Organization (WHO) on 31 December 2019 [4]. By 22 January 2020, a total of 571 cases of COVID-19 were reported in 25 provinces in China [5]. Despite the drastic, large-scale containment measures promptly implemented by the Chinese government, in a matter of a few weeks the disease had spread well outside China, and several countries have been facing with a global threat of the disease [2, 6, 7]. More than 210 countries of the world have been affected by COVID-19 epidemic [7], leading to its declaration as a global pandemic on 11 March 11 2020 by WHO [1, 8, 9].

Following the first positive confirmed case of COVID-19 in Singapore, the COVID-19 threat became more apparent in Malaysia as eight close contacts to the first case were identified to be in Johor [4]. On 25 January 2020, Malaysia announced its first (index) case of COVID-19 [10]. The first wave of the disease lasted from 24 January to 16 February 2020 with a number of cases totalling 22, which is mainly comprised infected individuals arriving from China [4]. The disease has spread very fast all over the country after 27 February 2020 due to the community transmission, establishing the beginning of its second wave [4]. On 5 April 2020, the number of cases increased to 3662 [10]. This spike in COVID-19 cases was attributed to a special religious gathering which took place between 27 February and 2 March 2020 at Sri Petaling mosque, whereby larger number of cases might be imported by the international participants [10]. Thus, the potential scale of COVID-19 epidemic became apparent in the country. According to [10], the sudden rise in COVID-19-confirmed cases could mean that the asymptomatic infected individuals could significantly spread the disease. Malaysia is currently experiencing the third wave of COVID-19, which broke out on 20 September 2020. By 31 December 2020, the number of reported cases of the pandemic has cumulated to 113,010, including 471 deaths, 88941 recovered cases, and 23598 active cases [11].

SARS-CoV-2 is an RNA virus from the family of Coronaviridae and genus Betacoronavirus [14]. RNA viruses have high rates of mutation. This feature profoundly influences disease emergence, viral evolution, appearance of drug resistances, and vaccine efficacy [12]. Then, it is critical to monitor the dynamics of SARS-CoV-2 mutation in order to understand its infectivity, virulence, and pathogenicity for a vaccine development [13]. In [14], the genetic epidemiology of SARS-CoV-2 in Malaysia was studied by sequencing four genomes from the country during the second wave of infection. The lineage B.6 strain was found to be predominant, implying a local evolution [14]. All the circulating strains in Malaysia were introduced from different countries. In October 2020, a new strain of the disease, D614G, was detected in Sabah state of the nation. It was reported that the strain is 10 times more infectious than the previous strains [15].

COVID-19 is a disease which targets the respiratory system of humans [5]. It is transmitted from human-to-human via direct contact with contaminated surfaces and by inhaling the respiratory droplets from COVID-19-infected humans during coughing and sneezing [4, 5, 16]. The incubation period for COVID-19 has been reported to range between 0 and 14 days, although a longer incubation period of 25 days is found in the literature [8]. The rate of recovery from the disease infection is higher than the mortality rate, but this ratio varies from one country to another as well as region to region [7]. The primary symptoms of COVID-19 are severe chest pain, high fever, body aches, headache, consistent dry coughing, and complication in the respiratory system [7].

Currently, there is no approved vaccine or a specific anti-viral treatment therapy to prevent or manage COVID-19, although several studies on vaccine invention are ongoing [5, 7]. Thus, control measures against the disease transmission are focusing on the use of basic non-pharmaceutical control interventions [8, 17]. These include movement control order, early detection, good hygiene practices [8], social distancing, use of face masks in public, quarantine of the suspected exposed individuals, isolation of positive (or confirmed) cases for prompt treatment, contact tracing [5, 8, 17], mandatory lockdowns, avoiding crowded events, imposing a maximum number on individuals in any gathering (religious and social) [5]. Currently, the most widely used control strategy for mitigating the pandemic spread is self-quarantine, wearing face masks while in public and social distancing [1]. To effectively reduce the spread and the prevalence of the disease in the affected countries, the concerned authorities have implemented many of these control intervention measures. However, individual nation also has its own policy in curbing the transmission dynamics of the disease in its territory [16].

To curb COVID-19 pandemic in Malaysia, a targeted testing approach has been announced by the government through the Ministry of Health in order to optimize the use of the limited medical resources available in the country. In targeted testing, tests are conducted on only high-risk groups at COVID-19 hotspot zones. However, some medical practitioners have questioned this approach, which reckon that COVID-19 testings should be conducted as wide as possible so that most (if not all) of the possible cases in the country would be detected. Then, the possible patients could be placed on a 14-day quarantine and be treated so as to contain the spread of the disease [18].

On 16 March 2020, the Malaysian Government announced a nationwide movement control order (MCO) to last between 18 and 31 March 2020 in order to mitigate the spread of COVID-19 through social distancing. The restricted activities prohibit all mass movements and gatherings across the country, including religious, sports, social, and educational activities. The movement control order was implemented in several stages with strict enforcement increasing with each stage to gain the public compliance to the restrictions [10]. MCO had been extended for a number of times [4].

From mathematical point of view, the transmission and control dynamics of several infectious diseases have been described by compartmental models governed by autonomous systems of ordinary differential equations (ODEs) in various works [1, 3, 5, 6, 8,9,10, 16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38]. These models help to facilitate the understanding of the mechanisms involved in the transmission dynamics of the diseases and gain insightful information about the efficacy of any implemented control intervention strategies in controlling their spread in a population. Several mathematical models have been formulated and analysed specifically for the dynamics of COVID-19 population in various countries ([1, 3, 6, 9, 10, 18, 20,21,22,23,24,25]), while the effects of different control intervention measures on the disease spread in a community have been evaluated using autonomous systems of ODEs in many other previous studies (e.g. see [5, 8, 16, 17, 26,27,28,29,30,31,32,33,34,35,36,37,38] and some of the references therein).

Using fractional differential operator approach, a mathematical model governing the evolution of COVID-19 epidemic in Italy was developed in [22]. Theoretical analysis of the fractional model suggests that the disease is stable if the basic reproduction number ${\mathcal {R}}_0$ is below unity. This result can be helpful in introducing appropriate interventions and design a suitable strategy for control implementation to effectively contain the disease transmission in the country. Similarly, Cooper et al. [1] used a mathematical model as a theoretical framework to examine the transmission dynamics of COVID-19 within a community. The model was applied to the disease outbreaks in six different countries that are China, South Korea, India, Australia, USA, and Italy. The model fitting makes use of the reported data between January and June 2020 (covering the period of movement control order and control measures) from each country. It was deduced from the study that the dynamics of COVID-19 can be under control in each of the communities under consideration, if proper restrictions and timely implementation of strong control policies are put in place to control the rates of infection.

In [20], a compartmental model was analysed to predict the dynamical behaviour of the infected individual subpopulation in the second wave of COVID-19 epidemic in Iran. Numerical simulations depict that the second wave of the disease will be more severe than the first. The authors observed that increasing the recovery rate of the infected humans by adopting necessary pharmaceutical measures is an essential strategy to prevent the disease incidence of a number of people. Also, Alsayed et al. [10] constructed a mathematical model to predict the peak and the number of infected cases of COVID-19 epidemic in Malaysia. The results of simulations show that the epidemic peak could be reached in the period ranging from 12 July to 11 August 2020, and last until the period ranging from 22 November 2020 to 12 January 2021.

The classical SIR model was adapted to analyse the epidemic of COVID-19 in Italy by D’Arienzo and Coniglio [25]. The model was analysed to assess the basic reproduction number, ${\mathcal {R}}_0$, associated with the model based on the reported data from the early phase of the disease outbreak in the country. The ${\mathcal {R}}_0$ value was estimated to range between 2.43and3.10, indicating the potential of the disease to invade the population. In a similar study [21], a compartmental mathematical model based on SEIR modelling structure was proposed for COVID-19 disease by specifically focusing on the super-spreaders individuals transmissibility. The local asymptotic dynamics of the model was discussed in terms of ${\mathcal {R}}_0$ associated with the model. The model was trained in data from reported cases of the epidemic outbreak in Wuhan, China.

Furthermore, a comparative assessment of the evolution of COVID-19 outbreaks in China, Italy, and France using a compartmental model based on SIR model framework was carried out in [6]. The model was used to analyse the effect of lockdown on the disease spread in the population for the time window 22 January to 15 March 2020. Numerical simulations indicate that implementation of lockdown control policy can help in reducing the epidemic peak and mortality rate in the countries under investigation.

In [5], a mathematical model was formulated and analysed to assess the impact of effective social distancing and face mask usage on COVID-19 population dynamics in Lagos, Nigeria. The simulated results of the model revealed that the disease will be eliminated in the population if about 55% of the population comply with the regulation of social distancing and about 55% of the population make effective use of face mask while in public. Liu et al. [26] also used a compartmental model to forecast the evolution of COVID-19 population with reference to the South Korea, Italy, and Spain epidemics. The model incorporates a time-varying disease transmission rate capturing the effect of government and social distancing control interventions. The study reveals that it is possible to contain the disease spread in the three countries. The authors warned that an early reduction in social distancing control policy or too extensive implementation of the control measure can lead to the disease epidemic entering a new phase.

A compartmental model incorporating the effects of vaccination and isolation intervention measures for the dynamics of COVID-19 population in Indonesia was proposed in [16]. The global asymptotic behaviour of the model was discussed in terms of its ${\mathcal {R}}_0$. The simulation results indicate that administration of vaccination control can accelerate the healing of COVID-19 infections and the disease spread can be slow down drastically by implementing the maximum effort of isolation control measure. In another work [9], a mathematical model taking into account the impact of healthcare capacity was formulated for the population dynamics of COVID-19 and control in Italy. Qualitative analysis of the model was carried out to reveal the global stability of the disease. The study suggests that the numbers of beds, ventilators, and intensive care units should be increased to considerably reduce the number of COVID-19 infections in the country.

Also, an intelligent computing paradigm based on Levenberg–Marquardt artificial neural networks was developed for the solution of mathematical model for COVID-19 population dynamics in metropolitans of Pakistan and China by Cheema et al. [54]. Ciufolini and Paolozzi [56, 60] carried out mathematical studies by using Gauss error function type to predict the evolution in time of the number of positive cases for COVID-19 outbreaks in Italy. In [61], two mathematical models were formulated to separately analyse the fast-growth phase and interpret the whole data set for China and South Korea COVID-19 outbreaks between 22 February and 20 May 2020. It was concluded that the models can be used in interpreting data and as prediction guide for the disease.

A deterministic model based on SIR framework was proposed to understand the evolution of COVID-19 outbreaks during lockdown and social distancing policy in Germany and Italy by Ianni and Rossi [57]. Similarly, Köhler-Rieper et al. [58] proposed a new approach to mathematical modelling of COVID-19 transmission dynamics by constructing a single ordinary integro-differential equation. It was shown that the model has similarities with the classical SIR model, and capable of predicting the disease outbreaks for a period of about 4 weeks.

Olaniyi et al. [59] formulated a deterministic model governing an autonomous system of ODEs for the dynamics of COVID-19 population in Nigeria. The study reveals that ${\mathcal {R}}_0$ value for the disease outbreak in the country can be reduced below one if the current disease effective transmission rate is lowered by 50%. Owing to this fact, the authors further used Pontryagin maximum principle to analyse the impacts of time-dependent preventive and management control measures in mitigating the spread of the disease. It was found that the number of infectious individuals can be reduced drastically by implementing the combined effort of the two control interventions.

It is evident that increasing the recovery rate of the infected humans by adopting necessary pharmaceutical measures is also an essential strategy to prevent COVID-19 incidence of a number of people in a population [20]. However, none of the previous studies has investigated the impacts of combining pharmaceutical and non-pharmaceutical measures in a bid to curtail the spread of COVID-19 in the community. Hence, a mathematical model involving an autonomous system of ODEs for COVID-19 population dynamics, which does not only used to assess the effect of non-pharmaceutical control measures but also pharmaceutical control interventions on the disease spread in Malaysia, is proposed in the present study. First, a basic COVID-19 model is developed and the nonlinear least square curve fitting approach is employed to estimate the model parameters by providing a good fit to the daily COVID-19-confirmed cases in Malaysia. Further, the basic model is modified to include five different control parameters accounting for personal protection (such as the use of hand sanitizer, face mask wearing, and social distancing policy), contact tracing and testing on the exposed individuals, and treatment controls of the timely diagnosed, delayed diagnosed, and hospitalized individuals to assess an effective strategy in mitigating the spread of COVID-19 in a population.

The remainder of this paper is organized in the following order: Sect. 2 presents the model description and formulation. Qualitative analysis of the basic properties of the model is discussed in Sect. 3. Model fitting is also considered. In Sect. 4, numerical simulations of the model are performed, and the results are also presented. This is followed up by detail discussions of results in Sect. 5. Section 6 provides a concluding remark of this study.

2 Model description and formulation

2.1 Basic COVID-19 mathematical model

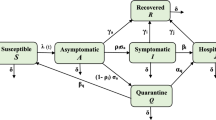
In formulating the compartmental model describing COVID-19 transmission dynamics, it is assumed that the total population is subgrouped into eight disjoint compartments at any time t. These are susceptible individuals, denoted as S(t), self-quarantined susceptible individuals, represented by $S_q(t)$, exposed (infected but not yet infectious) individuals, denoted as E(t), symptomatic (infectious) individuals, denoted as I(t), asymptomatic individuals, represented by A(t), quarantined individuals, denoted by Q(t), hospitalized individuals, denoted by H(t), and recovered individuals, represented as R(t). Thus, the total population at any time t, denoted as N(t), is given by

$$\begin{aligned} N(t)=S(t)+S_q(t)+E(t)+I(t)+A(t)+Q(t)+H(t)+R \end{aligned}$$

where N(t) has a variable size due to the consideration of the disease-induced death rate ($d\ne 0$).

Subpopulation of susceptible human is increased either by the recruitment of individuals at a rate of $\varLambda$ or by the fraction $\varepsilon S_q$ of the self-quarantined susceptible individuals, where $\varepsilon$ is the rate at which the self-quarantined susceptible individuals become susceptible to COVID-19 infection again. The subpopulation is decreased by the effective contact $\beta (I+\eta A+\rho H)S$, where $\beta$ is the effective transmission rate of COVID-19 virus from I, A and H classes to S, and $\eta$ and $\rho$ are the modification parameters accounting for the relative infectiousness of individuals in classes A and H in relation to the individuals in class I. Further, it is decreased by fraction $\omega S$, where $\omega$ is the migration rate of the susceptible individuals from class S to class $S_q$, and by natural death at rate $\mu$. Hence, the rate of change of susceptible human subpopulation is described by the differential equation given as

$$\begin{aligned} \frac{dS}{dt}=\varLambda +\varepsilon S_q-\beta (I+\eta A+\rho H)S-\omega S-\mu S. \end{aligned}$$

Self-quarantined susceptible individual subpopulation is generated at the rate of $\omega$ and decreased either at the rate of $\varepsilon$ or natural death rate $\mu$. Thus, the rate of change of subpopulation of self-quarantined susceptible human is represented as

$$\begin{aligned} \frac{dS_q}{dt}=\omega S-\varepsilon S_q-\mu S_q. \end{aligned}$$

Also, subpopulation of exposed (latently infected) individual is generated through the effective contact rate $\beta (I+\eta A+\rho H)S$. It is decreased by the rate $\sigma$ of exposed individuals either becoming symptomatic, asymptomatic, or hospitalized infected individuals and by natural death at rate of $\mu$. So, the rate of change of exposed individual subpopulation is given as

$$\begin{aligned} \frac{dE}{dt}=\beta (I+\eta A+\rho H)S-\sigma E-\mu E. \end{aligned}$$

Subpopulation of symptomatic infectious (delayed diagnosed) individual is generated by rate $\theta _1\sigma E$, where $\theta _1$ is the fraction of exposed individuals that move to the symptomatic infectious class I. It is decreased by the hospitalized rate $\alpha _i$, recovery rate $\gamma _i$, COVID-19-induced death rate d, and natural death rate $\mu$. Consequently, the rate of change of symptomatic infectious individual subpopulation is expressed as

$$\begin{aligned} \frac{dI}{dt}=\theta _1\sigma E-\alpha _iI-\gamma _iI-dI-\mu I. \end{aligned}$$

Similarly, asymptomatic infectious (early diagnosed) individual subpopulation is generated by the rate $\theta _2\sigma E$, where $\theta _2$ is the fraction of exposed individuals that progress to asymptomatic class A. The subpopulation is either decreased by the recovery rate of $\gamma _a$ or by natural death rate $\mu$. Thus, the rate of change of subpopulation of asymptomatic infectious individual is described by

$$\begin{aligned} \frac{dA}{dt}=\theta _2\sigma E-\gamma _aA-\mu A. \end{aligned}$$

In this case, the inflow rate is $\theta _2\sigma$ while the outflow rate is $\gamma _a+\mu$.

Moreover, quarantined infectious individual subpopulation is generated by the rate $\theta _3\sigma E$, where $\theta _3=1-\theta _1-\theta _2$ is the fraction of exposed individuals that progress to quarantined class Q. It is either decreased by the hospitalized rate $\alpha _q$, by recovery rate of $\gamma _q$, or by natural death rate $\mu$. Therefore, the rate of change of subpopulation of quarantined infected individual is represented as

$$\begin{aligned} \frac{dQ}{dt}=\theta _3\sigma E-\alpha _qQ-\gamma _qQ-\mu Q. \end{aligned}$$

Here, the inflow rate is $\theta _3\sigma$ and $\alpha _q+\gamma _q+\mu$ is the outflow rate.

Subpopulation of hospitalized infected individuals is generated by the inflow rate of $\alpha _iI+\alpha _qQ$. The subpopulation is decreased by an outflow rate including the recovery rate $\gamma _h$, disease-induced death rate d, and natural death rate $\mu$. It follows that the rate of change of hospitalized infected individual subpopulation is described by the differential equation given as

$$\begin{aligned} \frac{dH}{dt}=\alpha _iI+\alpha _qQ-\gamma _hH-dH-\mu H. \end{aligned}$$

Finally, the size of recovered individual subpopulation increases as a result of the recovery of hospitalized, quarantined, symptomatic, and hospitalized infected individuals at rates $\gamma _i$, $\gamma _a$, $\gamma _q$, and $\gamma _h$, respectively. It is decreased by natural death rate $\mu$. Hence, ODE governing the dynamic of recovered individual subpopulation is given by

$$\begin{aligned} \frac{dR}{dt}=\gamma _iI+\gamma _aA+\gamma _qQ+\gamma _hH-\mu R. \end{aligned}$$

Following the description above and the flow diagram of the COVID-19 model presented in Fig. 1, the model governing the system of eight mutually exclusive ODEs for COVID-19 population dynamic denotes as model (1) is expressed as

$$\begin{aligned} \frac{dS}{dt}&=\varLambda +\varepsilon S_q-\beta (I+\eta A+\rho H)S-\omega S-\mu S, \end{aligned}$$

(1a)

$$\begin{aligned} \frac{dS_q}{dt}&=\omega S-\varepsilon S_q-\mu S_q, \end{aligned}$$

(1b)

$$\begin{aligned} \frac{dE}{dt}&=\beta (I+\eta A+\rho H)S-\sigma E-\mu E, \end{aligned}$$

(1c)

$$\begin{aligned} \frac{dI}{dt}&=\theta _1\sigma E-\alpha _iI-\gamma _iI-dI-\mu I, \end{aligned}$$

(1d)

$$\begin{aligned} \frac{dA}{dt}&=\theta _2\sigma E-\gamma _aA-\mu A, \end{aligned}$$

(1e)

$$\begin{aligned} \frac{dQ}{dt}&=\theta _3\sigma E-\alpha _qQ-\gamma _qQ-\mu Q, \end{aligned}$$

(1f)

$$\begin{aligned} \frac{dH}{dt}&=\alpha _iI+\alpha _qQ-\gamma _hH-dH-\mu H, \end{aligned}$$

(1g)

$$\begin{aligned} \frac{dR}{dt}&=\gamma _iI+\gamma _aA+\gamma _qQ+\gamma _hH-\mu R, \end{aligned}$$

(1h)

where $\theta _3=1-\theta _1-\theta _2$. The parameters used in model (1) are defined in Table 1.

Fig. 1

Flow diagram of COVID-19 model (1), where $\lambda =\beta (I+\eta A+\rho H)$

Table 1 Description of the parameters for COVID-19 models (1) and (2)

2.2 COVID-19 mathematical model with effect of control

To examine the impact of both pharmaceutical and non-pharmaceutical control measures on the dynamics of COVID-19 population, we introduce five different bounded control parameters $\phi _i$ ($i=1,2,\ldots ,5$) defined as follows:

• $0\le \phi _1\le 1$: Effective effort of personal protection control measure (involving the use of hand-sanitizer, wearing face mask, and observing social distancing at any time they are in public) adopted by the population,

• $0\le \phi _2\le 1$: Control effort that accounts for contact tracing and testing on the exposed individuals to identify new cases,

• $0\le \phi _3\le 1$: Treatment control of timely diagnosed infected individuals,

• $0\le \phi _4\le 1$: Treatment control of delayed diagnosed infected individuals,

• $0\le \phi _5\le 1$: Treatment control measure of hospitalized infected individuals.

Incorporating the five control parameters above into basic COVID-19 model (1) leads to an autonomous system of ODEs governing the dynamics of transmission and control of COVID-19 denoted by model (2) given as

$$\begin{aligned} \frac{dS}{dt}&=\varLambda -\lambda S-(\omega +\mu )S+\varepsilon S_q, \end{aligned}$$

(2a)

$$\begin{aligned} \frac{dS_q}{dt}&=\omega S-(\varepsilon +\mu )S_q, \end{aligned}$$

(2b)

$$\begin{aligned} \frac{dE}{dt}&=\lambda S-(\sigma +\mu +\phi _2)E, \end{aligned}$$

(2c)

$$\begin{aligned} \frac{dI}{dt}&=\theta _1\sigma E-(\alpha _i+\gamma _i+d+\mu +\phi _4)I, \end{aligned}$$

(2d)

$$\begin{aligned} \frac{dA}{dt}&=\theta _2\sigma E-(\gamma _a+\mu +\phi _3)A, \end{aligned}$$

(2e)

$$\begin{aligned} \frac{dQ}{dt}&=\theta _3\sigma E-(\alpha _q+\gamma _q+\mu )Q+\phi _2E, \end{aligned}$$

(2f)

$$\begin{aligned} \frac{dH}{dt}&=(\alpha _i+\phi _4)I+\phi _3A+\alpha _qQ-(\gamma _h+d+\mu +\phi _5)H, \end{aligned}$$

(2g)

$$\begin{aligned} \frac{dR}{dt}&=(\gamma _h+\phi _5)H+\gamma _qQ+\gamma _iI+\gamma _aA-\mu R, \end{aligned}$$

(2h)

where $\lambda =(1-\phi _1)\beta (\eta A+I+\rho H)$ and $\theta _3=1-\theta _1-\theta _2$. Table 1 also gives the definitions of the parameters used in model (2).

3 Model analysis

3.1 Positivity and boundedness of solutions

For COVID-19 model (2) to be epidemiologically meaningful, it is necessary to show that all its state variables are positive for all time. In other words, the solutions of the model with positive initial data will remain positive for all time $t>0$.

Lemma 1

Let the initial data $X(0)\ge 0$, where $X(t)=(S(t),S_q(t),E(t),I(t),A(t),Q(t),H(t),R(t))$. Then, the solutions X(t) of COVID-19 model (2) are positive for all time $t>0$. In addition,

$$\begin{aligned} \underset{t\rightarrow \infty }{\lim \sup N(t)}\le \frac{\varLambda }{\mu }, \end{aligned}$$

where $N(t)=S(t)+S_q(t)+E(t)+I(t)+A(t)+Q(t)+H(t)+R(t)$.

Proof

Let $t_1=\sup \left\{ t>0:X(t)>0\in [0,t]\right\}$. Thus, $t_1>0$. It follows from Eq. (2a) that

$$\begin{aligned} \frac{dS(t)}{dt}=\varLambda +\varepsilon S_q(t)-\lambda (t)S(t)-(\omega +\mu ){S(t)}. \end{aligned}$$

(3)

Then, Eq. (3) can be written as

$$\begin{aligned} \frac{d}{dt}\left\{ S(t)\exp \left( \int _0^{t_1}\lambda (\zeta )\mathrm{d}\zeta +(\omega +\mu )t\right) \right\} =(\varLambda +\varepsilon S_q(t))\exp \left( \int _0^{t_1}\lambda (\zeta )\mathrm{d}\zeta +(\varepsilon +\mu )t\right) . \end{aligned}$$

Hence,

$$\begin{aligned}&S(t_1)\exp \left( \int _0^{t_1}\lambda (\zeta )\mathrm{d}\zeta +(\omega +\mu )t_1\right) -S(0)\\&\quad =\int _0^{t_1}(\varLambda +\varepsilon S_q(\tau ))\exp \left( \int _0^{\tau }\lambda (\zeta )\mathrm{d}\zeta +(\omega +\mu )\tau \right) \mathrm{d}\tau , \end{aligned}$$

so that

$$\begin{aligned} \begin{aligned} S(t_1)&=S(0)\exp \left[ -\left( \int _0^{t_1}\lambda (\zeta )\mathrm{d}\zeta +(\omega +\mu )t_1\right) \right] \\&\quad +\exp \left[ -\left( \int _0^{t_1}\lambda (\zeta )\mathrm{d}\zeta +(\omega +\mu )t_1\right) \right] \int _0^{t_1}(\varLambda +\varepsilon S_q(\tau ))\\&\quad \times \exp \left( \int _0^{t_1}\lambda (\zeta )\mathrm{d}\zeta +(\omega +\mu )t_1\right) \mathrm{d}\tau ,\\&\ge 0. \end{aligned} \end{aligned}$$

Thus, $S(t_1)$ is positive since it is a sum of positive terms. Similarly, it can be shown that $S_q(t)\ge 0$, $E(t)\ge 0$, $I(t)\ge 0$, $A(t)\ge 0$, $Q(t)\ge 0$, $H(t)\ge 0$, and $R(t)\ge 0$.

For the later part of the proof, note that $0<S(0)\le N(t)$, $0\le S_q(0)\le N(t)$, $0\le E(0)\le N(t)$, $0\le I(0)\le N(t)$, $0\le A(0)\le N(t)$, $0\le Q(0)\le N(t)$, $0\le H(0)\le N(t)$, $0\le R(0)\le N(t)$. Adding the components of COVID-19 model (2) gives

$$\begin{aligned} \frac{dN(t)}{dt}&=\varLambda -\mu N-d(I+H),\\&\le \varLambda -\mu N. \end{aligned}$$

Hence,

$$\begin{aligned} \underset{t\rightarrow \infty }{\lim \sup N(t)}\le \frac{\varLambda }{\mu } \end{aligned}$$

as required to be shown. $\square$

3.2 Invariant regions

The analysis of COVID-19 model (2) will be conducted with respect to a biologically feasible region as follows. Let $\varOmega \subset \mathbb {R}^8_+$, where $\varOmega$ is defined by Eq. (4) as

$$\begin{aligned} \varOmega =\left\{ (S(t),S_q(t),E(t),I(t),A(t),Q(t),H(t),R(t)):N(t)\le \frac{\varLambda }{\mu }\right\} . \end{aligned}$$

(4)

Lemma 2

The region $\varOmega$ in Eq. (4) is positively invariant for COVID-19 model (2) with non-negative initial conditions in $\mathbb {R}^8_+$.

Proof

By summing the equations of COVID-19 model (2), it follows that

$$\begin{aligned} \frac{dN(t)}{dt}&=\varLambda -\mu N-d(I+H),\\&\le \varLambda -\mu N. \end{aligned}$$

Hence, $\frac{dN(t)}{dt}\le 0$, if $N(0)\ge \frac{\varLambda }{\mu }$. Thus, $N(t)\le N(0)\exp \left\{ -\mu t\right\} +\frac{\varLambda }{\mu }\left( 1-\exp \left\{ -\mu t\right\} \right)$, implying that $N(t)\rightarrow \frac{\varLambda }{\mu }$ as $t\rightarrow \infty$. In particular, $N(t)\le \frac{\varLambda }{\mu }$ if $N(0)\le \frac{\varLambda }{\mu }$. Thus, the region $\varOmega$ is positively invariant set. Furthermore, if $N(0)>\frac{\varLambda }{\mu }$, then either the solutions enter the region $\varOmega$ in finite time, or N(t) approaches $\frac{\varLambda }{\mu }$ asymptotically. Hence, the region $\varOmega$ attracts all the solutions in $\mathbb {R}^8_+$. $\square$

Therefore, it is sufficient to consider COVID-19 transmission dynamics governed by model (2) in the biologically feasible region, $\varOmega$, where the model is both mathematically and epidemiologically well posed.

3.3 Existence of equilibrium points, basic reproduction number, and stability analysis

The equilibrium points associated with model (2) are defined such that there is no variations in the state variables S, $S_q$, E, I, A, Q, H, and R with respect to time, t.

Definition 1

An octuple $\mathcal E=\left( S,S_q,E,I,A,Q,H,R\right) \in \mathbb {R}^8$ is said to be an equilibrium point for COVID-19 model (2) if it satisfies

$$\begin{aligned}&\varLambda -\lambda S-(\omega +\mu )S+\varepsilon S_q=0, \end{aligned}$$

(5a)

$$\begin{aligned}&\omega S-(\varepsilon +\mu )S_q=0, \end{aligned}$$

(5b)

$$\begin{aligned}&\lambda S-(\sigma +\mu +\phi _2)E=0, \end{aligned}$$

(5c)

$$\begin{aligned}&\theta _1\sigma E-(\alpha _i+\gamma _i+d+\mu +\phi _4)I=0, \end{aligned}$$

(5d)

$$\begin{aligned}&\theta _2\sigma E-(\gamma _a+\mu +\phi _3)A=0, \end{aligned}$$

(5e)

$$\begin{aligned}&\theta _3\sigma E-(\alpha _q+\gamma _q+\mu )Q+\phi _2E=0, \end{aligned}$$

(5f)

$$\begin{aligned}&(\alpha _i+\phi _4)I+\phi _3A+\alpha _qQ-(\gamma _h+d+\mu +\phi _5)H=0, \end{aligned}$$

(5g)

$$\begin{aligned}&(\gamma _h+\phi _5)H+\gamma _qQ+\gamma _iI+\gamma _aA-\mu R=0, \end{aligned}$$

(5h)

where $\lambda =\beta (1-\phi _1)(I+\eta A+\rho H)$ and $\theta _3=1-\theta _1-\theta _2$.

It is important to note that equilibrium point ${\mathcal {E}}$ is biologically meaningful if and only if ${\mathcal {E}}\in \varOmega$. ${\mathcal {E}}$ can be a covid-free equilibrium (CFE) or covid-present equilibrium (CPE) depending on E, I, A, Q, and H. If COVID-19 is not present in the system (i.e. $E=I=A=Q=H=0$), then ${\mathcal {E}}$ is said to be CFE. Otherwise, if $E>0$, $I>0$, $A>0$, $Q>0$ or $H>0$, then ${\mathcal {E}}$ is called CPE.

To obtain CFE, it requires setting $E=I=A=Q=H=R=0$ in system (5). Consequently, CFE, denoted as ${\mathcal {E}}_f$, is obtained as

$$\begin{aligned} {{\mathcal {E}}}_f=\left( S^*,S_q^*,0,0,0,0,0,0\right) =\left( \frac{\varLambda (\varepsilon +\mu )}{\mu (\varepsilon +\omega +\mu )}, \frac{\varLambda \omega }{\mu (\varepsilon +\omega +\mu )},0,0,0,0,0,0\right) . \end{aligned}$$

(6)

Stability of CFE, ${\mathcal {E}}_f$, can be established by calculating the effective reproduction number, denoted as ${\mathcal {R}}_c$, using the next generation operator method studied in depth in [39] on COVID-19 model (2). Thus, ${\mathcal {R}}_c$ associated with model (2) is presented by Theorem 1.

Theorem 1

The effective reproduction number, ${\mathcal {R}}_c$, of COVID-19 model (2) is given as

$$\begin{aligned} {\mathcal {R}}_c&=\frac{(1-\phi _1)\beta (g_2g_4g_6\eta \theta _2\sigma +g_3g_4g_5\rho \theta _1\sigma +g_2g_3\rho \theta _3\sigma \alpha _q+g_2g_4\rho \theta _2\sigma \phi _3+g_3g_4g_6\theta _1\sigma +g_2g_3\rho \alpha _q\phi _2)S^*}{g_1g_2g_3g_4g_6}, \end{aligned}$$

(7)

$$\begin{aligned} {\mathcal {R}}_c&=\frac{(1-\phi _1)\beta (g_2g_4g_6\eta \theta _2\sigma +g_3g_4g_5\rho \theta _1\sigma +g_2g_3\rho \theta _3\sigma \alpha _q+g_2g_4\rho \theta _2\sigma \phi _3+g_3g_4g_6\theta _1\sigma +g_2g_3\rho \alpha _q\phi _2)\varLambda (\varepsilon +\mu )}{g_1g_2g_3g_4g_6\mu (\varepsilon +\omega +\mu )}, \end{aligned}$$

(8)

where $g_1=\sigma +\mu +\phi _2$, $g_2=\alpha _i+\gamma _i+d+\mu +\phi _4$, $g_3=\gamma _a+\mu +\phi _3$, $g_4=\alpha _q+\gamma _q+\mu$, $g_5=\alpha _i+\phi _4$, $g_6=\gamma _h+d\mu +\phi _5$, and $\theta _3=1-\theta _1-\theta _2$.

Proof

Taking E, I, A, Q and H as the infected compartments and then using the notation in [39], COVID-19 model (2) can be expressed as

$$\begin{aligned} \frac{d}{dt}\left( \begin{array}{c} E\\ I\\ A\\ Q\\ H\\ S\\ S_q\\ R \end{array} \right) =\left( \begin{array}{c} \lambda S\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0 \end{array} \right) -\left( \begin{array}{c} (\sigma +\mu +\phi _2)E\\ (\alpha _i+\gamma _i+d+\mu +\phi _4)I-\theta _1\sigma E\\ (\gamma _a+\mu +\phi _3)A-\theta _2\sigma E\\ (\alpha _q+\gamma _q+\mu )Q-\theta _3\sigma E-\phi _2E\\ (\gamma _h+d+\mu +\phi _5)H-(\alpha _i+\phi _4)I+\phi _3A+\alpha _qQ\\ \lambda S+(\omega +\mu )S-\varLambda -\varepsilon S_q\\ (\varepsilon +\mu )S_q-\omega S\\ \mu R-\gamma _iI-\gamma _aA-\gamma _qQ-(\gamma _h+\phi _5)H \end{array} \right) . \end{aligned}$$

(9)

The next generation matrices are obtained from Eq. (9) as

$$\begin{aligned} {\mathcal {F}}(x)=\left( \begin{array}{c} \lambda S\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0 \end{array} \right) , \quad {\mathcal {V}}(x)=\left( \begin{array}{c} (\sigma +\mu +\phi _2)E\\ (\alpha _i+\gamma _i+d+\mu +\phi _4)I-\theta _1\sigma E\\ (\gamma _a+\mu +\phi _3)A-\theta _2\sigma E\\ (\alpha _q+\gamma _q+\mu )Q-\theta _3\sigma E-\phi _2E\\ (\gamma _h+d+\mu +\phi _5)H-(\alpha _i+\phi _4)I+\phi _3A+\alpha _qQ\\ \lambda S+(\omega +\mu )S-\varLambda -\varepsilon S_q\\ (\varepsilon +\mu )S_q-\omega S\\ \mu R-\gamma _iI-\gamma _aA-\gamma _qQ-(\gamma _h+\phi _5)H \end{array} \right) , \end{aligned}$$

where $x^T=(E,I,A,Q,H)$. Then, infection matrix F and transition matrix V are the corresponding Jacobian matrices evaluated at ${\mathcal {E}}_f$ and are given as

$$\begin{aligned} F= & {} \left( \begin{array}{ccccc} 0 &{} \frac{(1-\phi _1)\beta \varLambda \eta (\varepsilon +\mu )}{\mu (\varepsilon +\omega +\mu )} &{} \frac{(1-\phi _1)\beta \varLambda \eta (\varepsilon +\mu )}{\mu (\varepsilon +\omega +\mu )} &{} 0 &{} \frac{(1-\phi _1)\beta \varLambda \rho (\varepsilon +\mu )}{\mu (\varepsilon +\omega +\mu )}\\ 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 \end{array} \right) , \\ V= & {} \left( \begin{array}{ccccc} g_1 &{} 0 &{} 0 &{} 0 &{} 0\\ -\theta _1\sigma &{} g_2 &{} 0 &{} 0 &{} 0\\ -\theta _2\sigma &{} 0 &{} g_3 &{} 0 &{} 0\\ -\theta _3\sigma -\phi _2 &{} 0 &{} 0 &{} g_4\\ 0 &{} -g_5 &{} -\phi _3 &{} -\alpha _q &{} g_6 \end{array} \right) , \end{aligned}$$

where $g_1=\sigma +\mu +\phi _2$, $g_2=\alpha _i+\gamma _i+d+\mu +\phi _4$, $g_3=\gamma _a+\mu +\phi _3$, $g_4=\alpha _q+\gamma _q+\mu$, $g_5=\alpha _i+\phi _4$, $g_6=\gamma _h+d+\mu +\phi _5$, and $\theta _3=1-\theta _1-\theta _2$.

Therefore, the effective reproduction number ${\mathcal {R}}_c$ is

$$\begin{aligned} {\mathcal {R}}_c&=\varrho \left( FV^{-1}\right) =\frac{(1-\phi _1)\beta (g_2g_4g_6\eta \theta _2\sigma +g_3g_4g_5\rho \theta _1\sigma +g_2g_3\rho \theta _3\sigma \alpha _q+g_2g_4\rho \theta _2\sigma \phi _3 +g_3g_4g_6\theta _1\sigma +g_2g_3\rho \alpha _q\phi _2)S^*}{g_1g_2g_3g_4g_6},\\ \mathcal R_c&=\frac{(1-\phi _1)\beta (g_2g_4g_6\eta \theta _2\sigma +g_3g_4g_5\rho \theta _1\sigma +g_2g_3\rho \theta _3\sigma \alpha _q+g_2g_4\rho \theta _2\sigma \phi _3+g_3g_4g_6\theta _1\sigma +g_2g_3\rho \alpha _q\phi _2)\varLambda (\varepsilon +\mu )}{g_1g_2g_3g_4g_6\mu (\varepsilon +\omega +\mu )}, \end{aligned}$$

where $g_1=\sigma +\mu +\phi _2$, $g_2=\alpha _i+\gamma _i+d+\mu +\phi _4$, $g_3=\gamma _a+\mu +\phi _3$, $g_4=\alpha _q+\gamma _q+\mu$, $g_5=\alpha _i+\phi _4$, $g_6=\gamma _h+d+\mu +\phi _5$, $\theta _3=1-\theta _1-\theta _2$, and $\varrho$ is the spectral radius. $\square$

Furthermore, using Theorem 2 in [39], the result in Lemma 3 immediately follows based on the expression ${\mathcal {R}}_c$.

Lemma 3

If ${\mathcal {R}}_c<1$, then CFE, ${\mathcal {E}}_f$, of COVID-19 model (2) is locally asymptotically stable (LAS), and unstable if ${\mathcal {R}}_c>1$.

Remark 1

From the expression ${\mathcal {R}}_c$ in Eq. (8), the basic reproduction number, denoted as ${\mathcal {R}}_0$, for the worst scenario of no control implementation (that is, $\phi _i=0$, $i=1,2,$..., 5) is obtained as

$$\begin{aligned} {\mathcal {R}}_0&={\mathcal {R}}_c|_{\phi _i=0,\ i=1,2,\ldots ,5}=\frac{\beta \sigma (\varepsilon +\mu )(\kappa _2\kappa _4\kappa _5\eta \theta _2 +\kappa _3\kappa _4\alpha _i\rho \theta _1+\kappa _2\kappa _3\rho \theta _3\alpha _q +\kappa _3\kappa _4\kappa _5\theta _1)\varLambda }{\kappa _1\kappa _2\kappa _3\kappa _4\kappa _5\mu (\varepsilon +\omega +\mu )}, \end{aligned}$$

(10)

$$\begin{aligned} {\mathcal {R}}_0&={\mathcal {R}}_{0I}+{\mathcal {R}}_{0A}+{\mathcal {R}}_{0H},\nonumber \\ {\mathcal {R}}_0&=\frac{\beta \sigma (\varepsilon +\mu )\theta _1\varLambda }{\kappa _1\kappa _2\mu (\varepsilon +\omega +\mu )} +\frac{\beta \sigma (\varepsilon +\mu )\eta \theta _2\varLambda }{\kappa _1\kappa _3\mu (\varepsilon +\omega +\mu )} +\frac{\beta \sigma (\varepsilon +\mu )\rho (\kappa _4\alpha _i\theta _1+\kappa _2\alpha _q\theta _3)\varLambda }{\kappa _1\kappa _2\kappa _4\kappa _5\mu (\varepsilon +\omega +\mu )}, \end{aligned}$$

(11)

where $\kappa _1=\sigma +\mu$, $\kappa _2=\alpha _i+\gamma _i+d+\mu$, $\kappa _3=\gamma _a+\mu$, $\kappa _4=\alpha _q+\gamma _q+\mu$, $\kappa _5=\gamma _h+d+\mu$ and $\theta _3=1-\theta _1-\theta _2$. Consequently, the expression ${\mathcal {R}}_0$ in (10) corresponds to the basic reproduction number of the uncontrolled COVID-19 model (1). The terms ${\mathcal {R}}_{0I}$, $\mathcal R_{0A}$ and ${\mathcal {R}}_{0H}$ in Eq. (11) represent the respective average numbers of new COVID-19 infections produced when the symptomatically, asymptomatically, and hospitalized infected individuals are introduced into a completely susceptible population.

Next, we determine the impact of each control measure in reducing COVID-19 disease burden in the population by following a similar idea in [40, 53]. Taking partial derivatives of reproduction number ${\mathcal {R}}_c$ with respect to control parameters $\phi _i$ (for $i=1,2,\ldots ,5$) gives

$$\begin{aligned} \frac{\partial {\mathcal {R}}_c}{\partial \phi _1}&=-\frac{\beta (\eta g_2g_4g_6\sigma \theta _2+g_2g_3\rho \sigma \alpha _q\theta _3+g_2g_4\rho \sigma \phi _3\theta _2 +g_3g_4g_5\rho \sigma \theta _1+g_2g_3\rho \alpha _q\phi _2+g_3g_4g_6\sigma \theta _1) \varLambda (\varepsilon +\mu )}{g_1g_2g_3g_4g_6\mu (\varepsilon +\omega +\mu )}<0,\\ \frac{\partial {\mathcal {R}}_c}{\partial \phi _2}&=\frac{(1-\phi _1)\beta \rho \alpha _q\varLambda (\varepsilon +\mu )}{g_1g_4g_6\mu (\varepsilon +\omega +\mu )}\\&\quad -\frac{(1-\phi _1)\beta (\eta g_2g_4g_6\sigma \theta _2+g_2g_3\rho \sigma \alpha _q\theta _3+g_2g_4\rho \sigma \phi _3\theta _3 +g_3g_5\rho \sigma \theta _1+g_2g_3\rho \alpha _q\phi _2+g_3g_4g_6\sigma \theta _1) \varLambda (\varepsilon +\mu )}{g_1^2g_2g_3g_4g_6\mu (\varepsilon +\omega +\mu )}<0,\\ \frac{\partial {\mathcal {R}}_c}{\partial \phi _3}&=-\frac{(1-\phi _1)\beta (\eta g_6-\rho (\gamma _a+\mu ))\sigma \theta _2\varLambda (\varepsilon +\mu )}{g_1g_3^2g_6\mu (\varepsilon +\omega +\mu )}<0,\\ \frac{\partial {\mathcal {R}}_c}{\partial \phi _4}&=-\frac{(1-\phi _1)\beta (g_6-\rho (\gamma _i+d+\mu ))\sigma \theta _1 \varLambda (\varepsilon +\mu )}{g_1g_2^2g_6\mu (\varepsilon +\omega +\mu )}<0,\\ \frac{\partial \mathcal R_c}{\partial \phi _5}&=\frac{(1-\phi _1)\beta (g_2g_4\eta \sigma \theta _2+g_3g_4\sigma \theta _1 )\varLambda (\varepsilon +\mu )}{g_1g_2g_3g_4g_6\mu (\varepsilon +\omega +\mu )}\\&\quad -\frac{(1-\phi _1)\beta (g_2g_4g_6\eta \sigma \theta _2+g_2g_3\rho \sigma \alpha _q\theta _3 +g_2g_4\rho \sigma \theta _2\phi _3+g_3g_4g_5\rho \sigma \theta _1+g_2g_3\rho \alpha _q\phi _2 +g_3g_4g_6\sigma \theta _1)\varLambda (\varepsilon +\mu )}{g_1g_2g_3g_4g_6^2\mu (\varepsilon +\omega +\mu )}<0. \end{aligned}$$

It follows that ${\mathcal {R}}_c$ is a decreasing function of $\phi _i$ (where $i=1,2,\ldots ,5$). This shows the effect of the five control measures in reducing the effective reproduction number $\mathcal R_c$. It is clear from Eqs. (8) and (10) that the introduction of controls $\phi _i$ implies that $\mathcal R_c\le {\mathcal {R}}_0$ for $0\le \phi _i\le 1$. Thus, if ${\mathcal {R}}_0<1$, then ${\mathcal {R}}_c<1$.

It is desirable to examine the solutions of COVID-19 model (2) when the virus is present in the population. Thus, the existence of CPE of COVID-19 model (2) is claimed in Theorem 2.

Theorem 2

If ${\mathcal {R}}_c>1$, then COVID-19 model (2) admits a unique (and positive) covid-present equilibrium (CPE) $\mathcal E_p=(S^{**},S_q^{**},E^{**},I^{**},A^{**},Q^{**},H^{**},R^{**})$, where

$$\begin{aligned} \begin{aligned} S^{**}&=\frac{\varLambda (\varepsilon +\mu )}{\mu (\varepsilon +\mu +\omega ){\mathcal {R}}_c},\\ S_q^{**}&=\frac{\varLambda \omega }{\mu (\varepsilon +\mu +\omega ){\mathcal {R}}_c},\\ E^{**}&=\frac{\varLambda ({\mathcal {R}}_c-1)}{g_1{\mathcal {R}}_c},\\ I^{**}&=\frac{\varLambda \theta _1\sigma ({\mathcal {R}}_c-1)}{g_1g_2{\mathcal {R}}_c},\\ A^{**}&=\frac{\varLambda \theta _2\sigma ({\mathcal {R}}_c-1)}{g_1g_3{\mathcal {R}}_c},\\ Q^{**}&=\frac{\varLambda (\theta _3\sigma +\phi _2)({\mathcal {R}}_c-1)}{g_1g_4{\mathcal {R}}_c},\\ H^{**}&=\frac{\varLambda {\mathcal {A}}({\mathcal {R}}_c-1)}{g_1g_2g_3g_4g_6{\mathcal {R}}_c},\\ R^{**}&=\frac{\varLambda {\mathcal {B}}(\mathcal R_c-1)}{g_1g_2g_3g_4g_6\mu {\mathcal {R}}_c}, \end{aligned} \end{aligned}$$

(12)

with $\mathcal A=g_3g_4g_5\theta _1\sigma +g_2g_4\phi _3\theta _2\sigma +g_2g_3\alpha _q(\theta _3\sigma +\phi _2)$, $g_7=\gamma _h+\phi _5$, and $\mathcal B=g_3g_4\theta _1\sigma (g_5g_7+g_6\gamma _i)+g_2g_4\theta _2\sigma (g_7\phi _3+g_6\gamma _a) +g_2g_3(\theta _3\sigma +\phi _2)(g_7\alpha _q+g_6\gamma _q)$. Otherwise, there is no CPE.

Proof

Here, system (5) is solved for the case $E>0$, $I>0$, $A>0$, $Q>0$, and $H>0$. Then, the steady solutions $S^{**}$ and $S_q^{**}$ are calculated by solving Eqs. (5a) and (5b) simultaneously to obtain

$$\begin{aligned} S^{**}=\frac{\varLambda (\varepsilon +\mu )}{(\lambda ^{**}+\mu )(\varepsilon +\mu )+\omega \mu } \end{aligned}$$

(13)

and

$$\begin{aligned} S_q^{**}=\frac{\varLambda \omega }{(\lambda ^{**}+\mu )(\varepsilon +\mu )+\omega \mu } \end{aligned}$$

(14)

It follows from Eq. (5c) that

$$\begin{aligned} E^{**}&=\frac{\lambda }{g_1}S^{**} \end{aligned}$$

and consequently,

$$\begin{aligned} E^{**}=\frac{\lambda ^{**}\varLambda (\varepsilon +\mu )}{g_1[(\lambda ^{**}+\mu )(\varepsilon +\mu )+\omega \mu ]}. \end{aligned}$$

(15)

From Eq. (5d),

$$\begin{aligned} I^{**}=\frac{\theta _1\sigma }{g_2}E^{**}. \end{aligned}$$

(16)

Also, from Eq. (5e),

$$\begin{aligned} A^{**}=\frac{\theta _2\sigma }{g_3}E^{**}. \end{aligned}$$

(17)

From Eq. (5f),

$$\begin{aligned} Q^{**}=\frac{(\theta _3\sigma +\phi _2)}{g_4}E^{**}. \end{aligned}$$

(18)

Moreover, from Eq. (5g),

$$\begin{aligned} H^{**}=\frac{{\mathcal {A}}}{g_2g_3g_4g_6}E^{**}, \end{aligned}$$

(19)

where $\mathcal A=g_3g_4g_5\theta _1\sigma +g_2g_4\phi _3\theta _2\sigma +g_2g_3\alpha _q(\theta _3\sigma +\phi _2)$. From Eq. (5h),

$$\begin{aligned} R^{**}=\frac{1}{\mu }\left[ \frac{g_7\mathcal A+g_2g_3g_6\gamma _q(\theta _3\sigma +\phi _2)+g_3g_4g_6\gamma _i\theta _1\sigma +g_2g_4g_6\gamma _a\theta _2\sigma }{}\right] E^{**}. \end{aligned}$$

(20)

Hence, the use of appropriate results in

$$\begin{aligned} \lambda ^{**}=(1-\phi _1)\beta (I^{**}+\eta A^{**}+\rho H^{**}) \end{aligned}$$

(21)

leads to

$$\begin{aligned}&\lambda ^{**}=(1-\phi _1)\beta \left( \frac{\theta _1\sigma }{g_2}+\frac{\eta \theta _2\sigma }{g_3}+\frac{\rho {\mathcal {A}}}{g_2g_3g_4g_6}\right) E^{**},\\&\lambda ^{**}=(1-\phi _1)\beta \left( \frac{g_3g_4g_6\theta _1\sigma +g_2g_4g_6\eta \theta _2\sigma +\rho {\mathcal {A}}}{g_2g_3g_4g_6}\right) \frac{\lambda ^{**}\varLambda (\varepsilon +\mu )}{g_1[(\lambda ^{**}+\mu )(\varepsilon +\mu )+\omega \mu ]},\\&g_1g_2g_3g_4g_6(\varepsilon +\mu )\lambda ^{**}+\mu (\varepsilon +\mu +\omega )g_1g_2g_3g_4g_6\\&\quad -\varLambda (1-\phi _1)\beta (\varepsilon +\mu )(g_3g_4g_6\theta _1\sigma +g_2g_4g_6\eta \theta _2\sigma +\rho \mathcal A)=0. \end{aligned}$$

This implies that

$$\begin{aligned}&g_1g_2g_3g_4g_6(\varepsilon +\mu )\lambda ^{**}+\mu (\varepsilon +\mu +\omega )g_1g_2g_3g_4g_6\\&\quad -\varLambda (1-\phi _1)\beta (\varepsilon +\mu )(g_3g_4g_6\theta _1\sigma +g_2g_4g_6\eta \theta _2\sigma +\rho {\mathcal {A}})=0,\\&g_1g_2g_3g_4g_6(\varepsilon +\mu )\lambda ^{**}+\mu (\varepsilon +\mu +\omega )g_1g_2g_3g_4g_6\\&\quad \left[ 1-\frac{\varLambda (1-\phi _1)\beta (\varepsilon +\mu )(g_3g_4g_6\theta _1\sigma +g_2g_4g_6\eta \theta _2\sigma +\rho \mathcal A)}{\mu (\varepsilon +\mu +\omega )g_1g_2g_3g_4g_6}\right] =0. \end{aligned}$$

Hence,

$$\begin{aligned}&g_1g_2g_3g_4g_6(\varepsilon +\mu )\lambda ^{**}+\mu (\varepsilon +\mu +\omega )g_1g_2g_3g_4g_6(1-{\mathcal {R}}_c)=0,\nonumber \\&\quad {\mathcal {C}}\lambda ^{**}+{\mathcal {D}}=0, \end{aligned}$$

(22)

where ${\mathcal {C}}=g_1g_2g_3g_4g_6(\varepsilon +\mu )$ and $\mathcal D=\mu (\varepsilon +\mu +\omega )g_1g_2g_3g_4g_6(1-{\mathcal {R}}_c)$.

Now, we deduce the condition for which $\lambda ^{**}$ is positive in Eq. (22). It should be noted from Eq. (22) that $\lambda ^{**}=\frac{-{\mathcal {D}}}{\mathcal C}\le 0$ if ${\mathcal {D}}\ge 0$ at ${\mathcal {R}}_c\le 1$, and no CPE exists. Contrarily, $\lambda ^{**}=-\frac{{\mathcal {D}}}{{\mathcal {C}}}>0$ if ${\mathcal {D}}<0$ at ${\mathcal {R}}_c>1$. Thus, a CPE exists only at ${\mathcal {R}}_c>1$. Hence, solving for $\lambda ^{**}$ in the linear Eq. (22) yields

$$\begin{aligned} \lambda ^{**}=\frac{\mu (\varepsilon +\mu +\omega )}{(\varepsilon +\mu )}(\mathcal R_c-1). \end{aligned}$$

(23)

Now, using the expression $\lambda ^{**}$ presented by Eq. (23) in Eq. (15) yields

$$\begin{aligned} E^{**}=\frac{\varLambda ({\mathcal {R}}_c-1)}{g_1{\mathcal {R}}_c}. \end{aligned}$$

(24)

Finally, substituting the expressions $\lambda ^{**}$ and $E^{**}$ in Eqs. (23) and (24), respectively, into Eqs. (13), (14), (16)–(20) accordingly leads to the results defined by Eq. (12). $\square$

3.4 Global asymptotic stability of the covid-free equilibrium ${\mathcal {E}}_f$

Since it has been demonstrated that CFE (${\mathcal {E}}_f$) and CPE (${\mathcal {E}}_p$) of COVID-19 model (2) are the unique equilibria, whose existence strongly depends on the ${\mathcal {R}}_c$ value, from the above discussion, the global asymptotic properties of CFE are explored in this section. To this aim, the idea of direct Lyapunov function used in [5, 41,42,43] is employed to show that CFE, ${\mathcal {E}}_f$, is globally asymptotically stable as follows. First, the following positive constant coefficients are defined:

$$\begin{aligned} \begin{aligned} a_1&=g_6,\\ a_2&=\frac{(1-\phi _1)\beta \varLambda (\varepsilon +\mu )(g_5\rho +g_6)}{g_2\mu (\varepsilon +\mu +\omega )},\\ a_3&=\frac{(1-\phi _1)\beta \varLambda (\varepsilon +\mu )(g_6\eta +\phi _3\rho )}{g_3\mu (\varepsilon +\mu +\omega )},\\ a_4&=\frac{(1-\phi _1)\beta \varLambda (\varepsilon +\mu )\rho \alpha _q}{g_4\mu (\varepsilon +\mu +\omega )},\\ a_5&=\frac{(1-\phi _1)\beta \varLambda (\varepsilon +\mu )\rho }{\mu (\varepsilon +\mu +\omega )}. \end{aligned} \end{aligned}$$

(25)

Now, consider the Lyapunov function ${\mathcal {L}}$ given as

$$\begin{aligned} {\mathcal {L}}=a_1E+a_2I+a_3A+a_4Q+a_5H. \end{aligned}$$

(26)

The time derivative of ${\mathcal {L}}$ in Eq. (26) is given by

$$\begin{aligned} \frac{d\mathcal L}{dt}&=a_1\frac{dE}{dt}+a_2\frac{dI}{dt}+a_3\frac{dA}{dt}+a_4\frac{dQ}{dt}+a_5\frac{dH}{dt},\nonumber \\&=\left[ a_2\theta _1\sigma +a_3\theta _2\sigma +a_4(\theta _3\sigma +\phi _2)-a_1g_1\right] E+\left[ a_1(1-\phi _1)\beta S+a_5g_5-a_2g_2\right] I\nonumber \\&\quad +\left[ a_1(1-\phi _1)\beta \eta S+a_5\phi _3-a_3g_3\right] A+(a_5\alpha _q-a_4g_4)Q+\left[ a_1(1-\phi _1)\beta \rho S-a_5g_6\right] H. \end{aligned}$$

(27)

Replacing $a_i$ ($i=1,\ldots ,5$) by their respective terms in Eq. (25) and using the fact that $S\le S^{*}=\frac{\varLambda (\varepsilon +\mu )}{\mu (\varepsilon +\omega +\mu )}$ in the feasible region $\varOmega$, we obtain

$$\begin{aligned} \frac{d{\mathcal {L}}}{dt}\le g_1g_6({\mathcal {R}}_c-1). \end{aligned}$$

(28)

From Eq. (28), we have $\frac{d{\mathcal {L}}}{dt}\le 0$ if ${\mathcal {R}}_c\le 1$, with $\frac{d{\mathcal {L}}}{dt}=0$ if $\mathcal R_c=1$ or $E=0$. Also, whenever $E=0$, we have $I=0$, $A=0$, $Q=0$ and $H=0$. Substituting $E=I=A=Q=H=0$ in the first, second, and the last equations of COVID-19 model (2) gives

$$\begin{aligned} S(t)\rightarrow S^*, \ S_q(t)\rightarrow S_q^* \ \text{ and } \ R(t)\rightarrow 0 \ \text{ as } \ t\rightarrow \infty . \end{aligned}$$

Thus,

$$\begin{aligned} \left( S(t),S_q(t),E(t),I(t),A(t),Q(t),H(t),R(t)\right) \rightarrow \mathcal E_f \ \text{ as } \ t\rightarrow \infty . \end{aligned}$$

Consequently, from LaSalle’s invariance principle [41, 43,44,45], every solution of COVID-19 model (2) with initial data in $\varOmega$ converges to CFE, ${\mathcal {E}}_f$, as $t\rightarrow \infty$. Therefore, CFE ${\mathcal {E}}_f$ is GAS in $\varOmega$ if $\mathcal R_c\le 1$. Thus, we claim the result summarized in Theorem 3.

Theorem 3

If ${\mathcal {R}}_c\le 1$, then CFE (${\mathcal {E}}_f$) of COVID-19 model (2) is GAS in $\varOmega$. Otherwise, it is unstable.

3.5 Parameter estimation and model fitting

The present section investigates data fitting using the basic model (1) to the confirmed reported COVID-19-infected cases in Malaysia. The available data for daily COVID-19-confirmed cases from 03 March 2020 (when the cases of the disease have continuously been reported per day) till 31 December 2020 reported in Malaysia are considered in this work. The data are obtained from [11] as given in Table 5. The data include the reported confirmed cases during the second and third waves of COVID-19 outbreaks in the country. The basic model (1) is parameterized using two approaches: Some of the initial conditions and demographic parameters are estimated from the literature. It is assumed that the time unit is days, and the estimation procedure for the initial conditions and parameters is described as follows:

• (i) On March 3, there were 7 reported cases (see Table 5); a total of 36 had so far been infected with 22 recovered and 14 active cases. So, we set $I(0)=7$, $H(0)=14$, and $R(0)=22$.

• (ii) Natural death rate ($\mu$): $\mu$ is estimated as $\mu =\frac{1}{75.93}$ per year, where 75.93 is the average lifespan in Malaysia [46]. Thus, $\mu =\frac{1}{75.93\times 365}$ per day.

• (iii) The birth or recruitment rate ($\varLambda$): Since the total population of Malaysia as at 2019 was 32581.4 (per thousands) [47], it is then assumed that $\frac{\varLambda }{\mu }=32581.4$ is the limiting total human population in the absence of the disease, so that $\varLambda =1.17561$ per day.

The remaining biological parameters and the likely values of the other initial conditions are trained with the reported infected cases presented in Table 5. To do this, we use the nonlinear least square curve fitting technique followed in [7, 40, 48, 49].

3.5.1 Results of the model fitting

Using the nonlinear least square curve fitting technique, fitting of model (1) to the daily reported COVID-19-infected cases in Malaysia is investigated. We consider the cumulative cases from the data presented in Table 5. The model is solved numerically in MATLAB with ode45 solver which is based on the fourth-order Runge–Kutta method. In [50], it is well established that this method is stable. So, the model is fit to real data, and the parameters are estimated by implementing the lsqcurvefit package. Figure 2 depicts the best fit to the reported data using model (1). It is observed that there is a good agreement between the model simulation and the real data. Also, Table 2 provides the estimated and fitted parameters values.

Fig. 2

Graphical illustration of the fitted cumulative number of reported COVID-19 cases

Table 2 Estimated parameter values and initial conditions for COVID-19 model (1)

3.6 Estimated ${\mathcal {R}}_0$ value and herd immunity

Using the model parameter values as given in Table 2, the estimated value of ${\mathcal {R}}_0$ is approximately $\mathcal R_0=2.287$. From biological view point, this threshold value indicates that COVID-19 will invade the population if no control effort is implemented to curtail the transmission and spread of the disease.

Based on the calculated ${\mathcal {R}}_0$ value, it is important to determine the fraction of the population that needs to be immunized in order to halt large outbreaks of COVID-19 in Malaysia. When high proportion of a population is immunized against a contagious infectious disease (either via vaccination or recovery from the disease infection), an indirect protection is provided to the proportion that is not immune to the disease. This kind of protection is called herd immunity [55, 62, 63]. Herd immunity plays a key role in epidemic control. For instance, it can be helpful in gaining insightful information about how effective a vaccination administration would be without reaching 100% population coverage.

Following [44, 63], the critical level of population immunity, denoted as ${\widehat{p}}$, is calculated with respect to the estimated ${\mathcal {R}}_0$ value for Malaysia COVID-19 outbreaks as

$$\begin{aligned} {\widehat{p}}=1-\frac{1}{{\mathcal {R}}_0}=0.56, \end{aligned}$$

implying that if 56% of the population is immune to COVID-19, then the disease will not spread in the population. Hence, successful vaccination of about 56% of the entire population may lead to eradication of the disease in Malaysia.

4 Numerical simulations and results

4.1 Uncertainty and global sensitivity analysis

Contrary to the local sensitivity analysis of model parameters approach [19, 43, 48], which is most often performed to assess the effect of each parameter included in the response function ${\mathcal {R}}_0$ at a particular point in a parameter space without considering the combined variability owing to the simultaneous consideration of all the input parameters, a global sensitivity analysis is discussed here. This helps to investigate the response of COVID-19 model (1) to parameter variation within a wider range in the parameter space.

Following the approach adopted in [5, 7], a Latin Hypercube Sampling (LHS) is conducted because of the uncertainties that may come up in the parameter estimates used in the numerical simulations. For the sensitivity analysis, a Partial Rank Correlation Coefficient (PRCC) between the values of the parameters in the response function and those of the response function obtained from the sensitivity analysis is carried out. Using the basic reproduction number ${\mathcal {R}}_0$ as the response function, parameters with the highest PRCC values have the largest impact on ${\mathcal {R}}_0$. Therefore, the key parameters influencing $\mathcal R_0$ are separated into those that decrease ${\mathcal {R}}_0$ when increased (bars extending to the left for negative PRCC values) and those that cause ${\mathcal {R}}_0$ to increase when increased (bars extending to the right for positive PRCC values). Performing 1000 runs of the LHS, the graphical PRCC results of COVID-19 model (1) relative to the parameters forming ${\mathcal {R}}_0$ are shown in Fig. 3. Figure 3 observes that the top-ranked sensitive parameter with high positive PRCC value that drives the dynamics of the model transmission is $\beta$, followed by $\varLambda$, $\rho$, $\varepsilon$, $\alpha _q$, $\sigma$, $\theta _2$, $\eta$, and $\theta _1$. Similarly, the model parameters with competitive most high negative PRCC value are $\mu$, then $\omega$, $\gamma _h$, $\gamma _q$, d, $\gamma _i$, $\alpha _i$, and $\gamma _a$.

Fig. 3

PRCC values for COVID-19 model (1) using ${\mathcal {R}}_0$ as the response function with respect to the parameter range and baseline values given in Table 2

In addition, the sensitivity indices of the model parameters are presented in Table 3. On the one hand, the positive sign suggests that increasing (or decreasing) any of the model parameter values in this category will lead to a corresponding increase (or decrease) in ${\mathcal {R}}_0$ value. The negative sign, on the other hand, indicates that increasing (or decreasing) each model parameter value in this category will yield a corresponding decrease (or increase) in ${\mathcal {R}}_0$ of the model.

It is important to identify these key parameters because they can be helpful to the decision makers and the public health practitioners in formulating effective control intervention strategies required to contain the disease spread in the community. Particularly, the results obtained from the sensitivity analysis indicate that a control intervention strategy aims at reducing the model parameters with positive PRCC values (that is, $\eta$, $\varepsilon$, $\beta$, $\theta _2$, $\rho$, $\theta _1$, $\varLambda$, $\alpha _q$, and $\sigma$) will considerably mitigate the spread of COVID-19 in the community. In addition, the transmission dynamics of COVID-19 can be effectively curtailed in a community by implementing a control strategy that increases the model parameters having negative PRCC values (that is, $\omega$, $\gamma _a$, d, $\mu$, $\gamma _h$, $\gamma _i$, $\alpha _i$, and $\alpha _q$).

Table 3 Sensitivity indices of the basic reproduction number ${\mathcal {R}}_0$ to the parameters of model (1)

4.2 Assessing the effects of control intervention strategies

This section discusses the numerical simulations of controlled COVID-19 model (2) to assess the impacts of using control interventions $\phi _1$ (human personal protection including the use of hand-sanitizer, wearing face mask and observing social distancing whenever in public), $\phi _2$ (efforts of contact tracing and testing on exposed individuals), $\phi _3$ (treatment of timely diagnosed individuals), $\phi _4$ (treatment of delayed diagnosed individuals), and $\phi _5$ (treatment of hospitalized individuals) on the spread of COVID-19 in the population.

4.2.1 Effects of control interventions on the effective reproduction number ${\mathcal {R}}_c$

According to the epidemiological interpretation of Lemma 3 and Theorem 3, COVID-19 will eventually die out in the population when ${\mathcal {R}}_c<\mathcal R_0<1$, and invades the population whenever ${\mathcal {R}}_0>\mathcal R_c>1$. Since ${\mathcal {R}}_0=2.287>1$ in the case of no control interventions for COVID-19 outbreaks under investigation, we specifically explore the effects of using two different control intervention strategies simultaneously in putting the effective reproduction number ${\mathcal {R}}_c$ expressed in Eq. (8) below unity. Figure 4a–c demonstrates the effects of using control strategies which combine controls $\phi _1$ and $\phi _2$, $\phi _3$ and $\phi _5$, and $\phi _4$ and $\phi _5$, respectively.

Fig. 4

Contour plots of ${\mathcal {R}}_c$

Figure 4a shows that the reduction in effective reproduction number ${\mathcal {R}}_c$ below unity is possible by combining about 0.56 (56%) effort each of controls $\phi _1$ and $\phi _2$. This suggests that it is possible to eliminate COVID-19 in the population if about 56% of the population comply with personal protection control and about 56% of the exposed individuals that are early diagnosed (through the implementation of control $\phi _2$) effectively comply with the compulsory quarantine policy per day. Also, it is observed that the simultaneous implementation of about 0.07 (7%) proportion of controls $\phi _3$ and $\phi _5$ (Fig. 4b) effectively impacts ${\mathcal {R}}_c$ to decrease below unity. The result indicates that it is possible to eliminate COVID-19 in the population, if about 7% of the hospitalized individuals get timely treatment support and about 7% of early diagnosed exposed individuals receive treatment support throughout the control implementation period. Figure 4c shows the effective impact of combining about 0.09 (9%) proportion of controls $\phi _4$ and $\phi _5$ by reducing ${\mathcal {R}}_c$ below the acceptable level (${\mathcal {R}}_c<1$). This implies that eradication of COVID-19 in the population is possible if about 9% of delayed diagnosed (symptomatic infected) individuals and about 9% of the hospitalized individuals are treated daily over the simulation period.

4.2.2 Effects of different control strategies A–E on COVID-19 population dynamics

Here, we evaluate the effects of using combination of at least two of controls $\phi _i$ ($i=1,2,\ldots ,5$) on the transmission dynamics of COVID-19 in the community. For this aim, five different control strategies are defined with consideration of only non-pharmaceutical, only pharmaceutical, and combination of pharmaceutical and non-pharmaceutical control measures implementation scenarios. The strategies are: Strategy A (non-pharmaceutical measure only; which combines the use of human personal protection, $\phi _1$, and contact tracing and testing, $\phi _2$, controls), Strategy B (pharmaceutical measure only; combined efforts of treatment control of timely diagnosed individuals, $\phi _3$, with treatment control of hospitalized individuals, $\phi _5$), Strategy C (pharmaceutical measure only; simultaneous implementation of treatment control of delayed diagnosed individuals, $\phi _4$, and treatment control of hospitalized individuals, $\phi _5$), Strategy D (pharmaceutical measure only; which combines the treatment control efforts of early diagnosed individuals, $\phi _3$, treatment control of delayed diagnosed individuals, $\phi _4$, and treatment control of hospitalized individuals, $\phi _5$) and Strategy E (pharmaceutical and non-pharmaceutical measures; combination of personal protection control, $\phi _1$, contact tracing and testing control, $\phi _2$, treatment control of early diagnosed individuals, $\phi _3$, treatment control of delayed diagnosed individuals, $\phi _4$, and treatment control of hospitalized individuals, $\phi _5$).

To illustrate the effect of implementing Strategies A–E, the time series solutions of self-quarantined individual subpopulation ($S_q$), subpopulation of symptomatic infectious individual (I), the disease prevalence (including the numbers of exposed, E, asymptomatic infected, A, symptomatic infected, I, quarantined, Q, and hospitalized, H, individuals), and recovered individual subpopulation (R) are presented.

4.2.3 Strategy A: combination of use of personal protection ($\phi _1$) and contact-tracing policy ($\phi _2$)

Figure 5 shows the dynamics of COVID-19 population with the use of Strategy A and when no control is implemented. It is observed that the number of self-quarantined individuals peak between 1 and 10 days from the beginning of pandemic outbreak and the subpopulation with control is more consistently maintained at the peak value over the remaining simulation period than the subpopulation without control (see Fig. 5a). Figure 5b and c reveals that there are three pandemic peaks, where the first one occurs between 250 and 400 days (from March 3, 2020) in the absence of personal protection and contact-tracing and testing policy controls implementation, the second occurs after 350 days (by February 2021) when 20% of the entire population observe personal protection control measure and 20% of the detected exposed individuals comply with compulsory self-quarantine policy while the third occurring after 600 days (by October 2021) when 40% of the population comply with personal protection regulation and 40% of the exposed individuals that are detected comply with compulsory self-quarantine policy. The peak vanishes when 60% of the population make use of personal prevention measure and 60% of the detected exposed individuals comply with self-quarantine policy. The number of symptomatic infectious individuals and the size of the disease prevalence in the population diminish more rapidly and quickly with control strategy than when there is no control (as shown in Fig. 5b and c), leading to fewer number of individuals recovering from COVID-19 infection (as shown in Fig. 5d).

This control strategy reveals that, if about 60% of the population comply with the personal protection control policy (such as the use of hand sanitizer, observing social distancing and effective wearing of face mask in public), at least 60% of the exposed individuals that are detected comply with the compulsory quarantine policy, and with strict enforcement of self-quarantine (lockdown) on the entire population, then it is possible to eliminate the pandemic in the community.

Fig. 5

Simulations of model (2) with Strategy A and without control

Fig. 6

Simulations of model (2) with strategy B and without control

4.2.4 Strategy B: combination of use of treatment of timely diagnosed individuals ($\phi _3$) and treatment of hospitalized individuals ($\phi _5$)

In Fig. 6, the effect of implementing Strategy B on the dynamics of COVID-19 population is illustrated. Figure 6a indicates that the self-quarantined subpopulation peaks between 1 and 10 days (counting from March 3, 2020), and the subpopulation with control is consistently sustained at the peak value throughout the remaining intervention period. It can be seen that COVID-19 incidence and prevalence diminish when timely treatment is administered on about 20% of early diagnosed individuals and about 20% of hospitalized individuals per day (see Fig. 6b and c). Further, the use of this strategy causes fewer number of individuals to recover from COVID-19 infection as shown in Fig. 6d. Hence, the results obtained from implementing this control strategy suggest that it is possible to flatten COVID-19 pandemic curve if about 20% of early diagnosed individuals and about 20% of hospitalized individuals receive treatment support per day, with strictly enforced self-quarantined (lockdown) on the entire population.

4.2.5 Strategy C: combination of use of treatment of delayed diagnosed individuals ($\phi _4$) and treatment of hospitalized individuals ($\phi _5$)

Figure 7 depicts the effect of combining treatment controls of delayed diagnosed and hospitalized individuals (Strategy C) on the dynamics of COVID-19 population. It is observed that the number of self-quarantined individual is peaked between 1 and 10 days from the beginning of the pandemic outbreak, and the number with control is more continuously maintained at the peak value over the remaining intervention period as shown in Fig. 7a. Figure 7b and c depicts that the use of about 20% each of controls $\phi _4$ and $\phi _5$ diminishes the incidence and prevalence of COVID-19 in the population. In addition, the number of recovered individuals is significantly reduced with an increased combined efforts of control implementation as observed in Fig. 7d. Hence, this strategy indicates that it is possible to eradicate COVID-19 in the population, if about 20% of both the delayed diagnosed and hospitalized individuals in the population get treated per day and self-quarantine policy is strictly enforced on the entire population.

Fig. 7

Simulations of model (2) with strategy C and without control

4.2.6 Strategy D: combination of use of treatment of timely diagnosed, delayed diagnosed and hospitalized individuals ($\phi _3$, $\phi _4$ and $\phi _5$)

Figure 8 demonstrates the effect of the use of Strategy D (combined efforts of controls $\phi _3$, $\phi _4$ and $\phi _5$) on the transmission dynamics of COVID-19 in the population. It is seen that using about 20% of each control, the number of self-quarantined is consistently sustained at the peak value for almost the entire intervention period when compared with the case of no control implementation (see Fig. 8a). Also, Fig. 8b and c shows one pandemic peak occurring between 250 and 400 days (counting from March 3, 2020) when no pharmaceutical measures are implemented. However, this pandemic peak disappears over the simulation period by implementing about 20% each of the treatment controls of timely diagnosed, delayed diagnosed and hospitalized individuals on a daily basis. Consequently, a high number of infections are averted with control implementation as the size of recovered individual sub-population significantly decreases when compared with the worst scenario of no control implementation in the population as observed in Fig. 8d. Therefore, the use of Strategy D suggests that if self-quarantine policy is strictly enforced on the entire population with about 20% each of early diagnosed, delayed diagnosed, and hospitalized individuals given timely treatment per day, then it is possible to eliminate COVID-19 in the population in the long run.

Fig. 8

Simulations of model (2) with strategy D and without control

4.2.7 Strategy E: combination of use of personal protection ($\phi _1$), contact-tracing policy ($\phi _2$), and treatment of timely diagnosed, delayed diagnosed and hospitalized individuals ($\phi _3$, $\phi _4$ and $\phi _5$)

The dynamics of COVID-19 population with and without the implementation of control Strategy E is illustrated in Fig. 9. Figure 9a shows that with the use of about 20% each of controls $\phi _i$ ($i=1,2,\ldots ,5$), the size of self-quarantined subpopulation is consistently maintained at the peak value after about 10th day till the end of intervention period. Also, the peaks of symptomatic infectious individual sub-population and the disease prevalence occurring between 250 and 400 days (counting from March 3, 2020) in the case of no control implementation disappeared from the onset of control implementation till the end of control implementation period by using 20% of each control (as shown in Fig. 9b and c) leading to no individuals recovering from COVID-19 infections in the population (see Fig. 9d). It therefore follows from the implementation of this control strategy that elimination of COVID-19 in the population is possible if the self-quarantined policy (lockdown) is strictly enforced on the whole population with about 20% of the population complying with personal protection control policy, about 20% of the detected exposed individuals obeying the compulsory quarantine policy, about 20% of the early diagnosed, delayed diagnosed, and hospitalized individuals receiving medical treatment per day.

Fig. 9

Simulations of model (2) with strategy E and without control

4.3 Effectiveness analysis

Graphical solutions illustrated in Figs. 6, 7, 8, 9 show that implementations of Strategies B–E have similar impacts on the dynamics of COVID-19-infected subpopulations and the disease prevalence. Thus, it is necessary to compare the efficacy of control intervention strategies A–E in reducing COVID-19 prevalence in the population by performing effectiveness analysis in the current section. This helps us in our decision making on the best control intervention strategy. Following [51,52,53], we compare the efficacy of the five strategies under investigation in reducing COVID-19 prevalence (including exposed, asymptomatic, symptomatic, quarantined, and hospitalized individuals) in the population. To this aim, effectiveness index is defined as [51,52,53]:

$$\begin{aligned} {\mathcal {C}}_i=\left( 1-\frac{{\mathcal {C}}_s}{\mathcal C_o}\right) \times 100\% \end{aligned}$$

(29)

where ${\mathcal {C}}_s=\int _0^T(E+A+I+Q+H)\mathrm{d}t$ and $\mathcal C_o=\int _0^T(E+A+I+Q+H)\mathrm{d}t$ measure the cumulative number of infected individuals (COVID-19 prevalence) in the time interval $t\in [0, T]$, $T=1400$ days, with and without any control intervention, respectively. Thus, the best control strategy will be the one with the biggest ${\mathcal {C}}_i$ value [51, 53].

Using the simulation results for control strategies A–E (as shown in Figs. 5, 6, 7, 8, 9) and fixing controls $\phi _i$ $(i=1,2,\ldots ,5)$ at $0.60(60\%)$ since the disease spread is significantly curtailed at this level of control implementation for each control strategy, the results of effectiveness index are summarized in Table 4.

Table 4 Effectiveness index

Table 4 shows that Strategy E (which combines personal protection, contact tracing and testing of exposed individuals, treatment of early diagnosed individuals, treatment of delayed diagnosed individuals, and treatment of hospitalized individuals control efforts) is the most effective, followed by Strategy D (which combines treatment controls of early diagnosed, delayed diagnosed, and hospitalized individuals), Strategy B (combination of treatment controls of early diagnosed and hospitalized individuals), Strategy C (which combines the efforts of treatment control of delayed diagnosed and hospitalized individuals), then Strategy A (combination of personal protection and contact tracing and testing of exposed individuals controls). In other words, the control strategy that averts the highest number of infections in the population is Strategy E. Strategy D is the next strategy that averts the highest number of COVID-19 infections, followed by Strategies B and C, while Strategy A averts the least number of infections in the population.

5 Discussion

In this work, we consider the daily confirmed COVID-19 cases from 3 March 2020 (the first day from when the disease started to be reported continuously on daily basis) to 31 December 2020 in Malaysia. Since it has been demonstrated that deterministic models fit well to cumulative COVID-19-infected cases in several previous studies [5, 7, 48], the parameters of the autonomous system (1) are fitted using the cumulative version of the data set given in Table 5. Using the fitted parameter values along with the initial values in Table 2, the projection of the number of infected individuals (I), recovered individuals (R), and the disease prevalence (including the exposed individuals E, symptomatic infectious individuals, I, asymptomatic infectious individuals, A, quarantined individuals, Q, and hospitalized individuals, H) in Figs. 5, 6, 7, 8,9 reveals that it may take about 600 days (counting from 3 March 2020) before the number of COVID-19-confirmed cases diminishes, while it takes about 650 days (from 3 March 2020) before the disease infection could be cleared in the population after all the patients having recovered from infection in the case of no control implementation. Also, the estimated basic reproduction number ${\mathcal {R}}_0$ value is approximately ${\mathcal {R}}_0=2.287$. This threshold value is an epidemiological indicator that COVID-19 will persist in the population when no control effort is implemented. Hence, it is desirable to investigate a control strategy that puts ${\mathcal {R}}_0$ below one.

To this aim, five control parameters accounting for personal protection (such as the use of hand sanitizer, effective wearing of face mask whenever in public, observing social distancing), contact tracing and testing to quarantine the latently infected (exposed) individuals, and treatment controls of the timely diagnosed, delayed diagnosed and hospitalized individuals are introduced into the model. First, we use the corresponding effective reproduction number ${\mathcal {R}}_c$ as a response function to examine the impact of different control strategies involving the use of exactly two control measures with no consideration for combining a pharmaceutical control measure (either treatment of early diagnosed, delayed diagnosed, or hospitalized individuals) with any non-pharmaceutical control measures (human personal protection or case detection through contact tracing and testing). Figure 4 shows that Strategies A (use of non-pharmaceutical control measures only), B (use of pharmaceutical controls; treatment controls of early diagnosed and hospitalized individuals only) and C (use of pharmaceutical controls; treatment controls of delayed diagnosed and hospitalized individuals) are all sufficient to put ${\mathcal {R}}_c$ below unity within the bound imposed on the control parameters (i.e. $\phi _i\in [0,1], \ i=1,2,\ldots ,5$). However, least combined effort of controls (about 0.07 of each control) is needed in lowering ${\mathcal {R}}_c$ below unity using Strategy B, while the use of Strategies C and A requires more and most combined effort of controls involved (about 0.09 and 0.58, respectively) in reducing ${\mathcal {R}}_c$ below the acceptable level for disease elimination in the community. The observed significant impact of applying non-pharmaceutical control measures on ${\mathcal {R}}_c$ agrees with the results in [5], which revealed that the implementation of combined efforts of face mask and social distancing control measures is enough to bring $\mathcal R_c$ below one in the long run.

Moreover, we investigate the effects of Strategies A–E on the dynamics of COVID-19 population. We observed that the number of symptomatic infectious individuals as well as the disease prevalence can be reduced considerably in the population using any of the five control strategies (see Figs. 5, 6, 7, 8, 9). It is possible to flatten the epidemic curve using about 0.20 (20%) combined control effort involved in Strategies B–E per day, while a covid-free population can be achieved using Strategy A by stepping up the combined effort of controls to 0.60 (60%) per day over the simulation period. It is shown that a positive attitude of the entire population toward self-isolation may enhance the efficacy of the implemented personal protection, contact tracing and testing on exposed individuals, and treatment control measures using any of Strategies A–E analysed in this work (see Figs. 5a, 6a, 7a, 8a and 9a). The effect of the six control strategies is analysed at 0% to 60% levels of implementations because it is more realistic to admit the possibility of the public compliance with human personal protection and the use of other practical control measures (treatment and contact tracing and testing) at these levels than their higher levels of implementations (i.e. 61%–100%).

6 Conclusion

This work has formulated and analysed an appropriate mathematical model which involves an autonomous system of ODEs governing the dynamics of COVID-19 population in Malaysia. The model is used to evaluate the impact of different control strategies for the use of pharmaceutical control measures (particularly, treatment of early diagnosed, delayed diagnosed and hospitalized individuals) and non-pharmaceutical interventions (human personal protection, such as the use of hand-sanitizer, social distancing policy and wearing of face mask, and case detection through contact tracing ad testing on the exposed individuals) on the disease spread dynamics.

Qualitative analysis of the model reveals that the model has a CFE, which is LAS whenever ${\mathcal {R}}_c<1$ and GAS if $\mathcal R_c\le 1$. It is also shown that the model admits a unique CPE if ${\mathcal {R}}_c>1$, and no CPE otherwise.

Sensitivity analysis of the model parameters reveals that the transmission probability of the virus ($\beta$), progression rate of susceptible individuals to self-quarantined compartment ($\omega$), the rate of self-quarantined individuals to become susceptible to COVID-19 virus again ($\varepsilon$), human recruitment rate ($\varLambda$), modification parameter representing the relative infectiousness of hospitalized individuals ($\rho$), progression rate of quarantined individuals to hospitalized compartment ($\alpha _q$), human natural death rate ($\mu$), COVID-19 induced death rate (d), recovery rate of hospitalized individuals ($\gamma _h$), and recovery rate of quarantined individuals ($\gamma _q$) among other parameters are the dominant parameters influencing the basic reproduction number ${\mathcal {R}}_0$.

By performing numerical simulations of the model, the effects of using control Strategies A–E (where Strategy A is the combination of personal protection and contact tracing and testing control measures, Strategy B is the simultaneous administration of treatment control on early diagnosed and hospitalized infected individuals, Strategy C is the combined efforts of treatment controls administered on the delayed diagnosed and hospitalized infected individuals, Strategy D combines the treatment controls of early diagnosed, delayed diagnosed, and hospitalized infected individuals, while Strategy E is the combination of personal protection, contact tracing and testing on exposed individuals, and treatment controls of early diagnosed, delayed diagnosed and hospitalized individuals) on the dynamics of COVID-19 spread in the community are analysed. It is found that using Strategy A (non-pharmaceutical control measures only), COVID-19 will eventually die out in the population if at least 60% of the population comply with personal protection policy such as effective use of face mask while in public, observing social distancing, regular use of hand sanitizer among others with about 60% of detected exposed individuals comply with the compulsory quarantine policy. Also, it is possible to eliminate the disease in the population when only pharmaceutical measures are implemented, if about 20% of early diagnosed individuals is given timely treatment with at least 20% of the hospitalized individuals being provided with timely treatment (Strategy B), if at least 20% of the delayed diagnosed individuals receives timely treatment and timely treatment is administered on about 20% of the hospitalized individuals (Strategy C), or if about 20% of early diagnosed individuals is given timely treatment with at least 20% of each of the delayed diagnosed and hospitalized individuals given timely treatment. However, it is most effective to eliminate the disease in the population using combination of pharmaceutical and non-pharmaceutical control measures (Strategy E), if about 20% of the population comply with personal protection regulation with about 20% of the detected exposed individuals comply with quarantine policy, and early treatment is administered on at least 20% of each early diagnosed, delayed diagnosed and hospitalized individuals.

Therefore, this work suggests combination of pharmaceutical and non-pharmaceutical measures including strict enforcement of personal protection (such as the use of hand sanitizer, social distancing compliance and use of face mask among others), population screening and testing to detect new cases, provision of a timely treatment support for the early diagnosed, delayed diagnosed and hospitalized infected individuals along with lockdown imposed on the population as a strict measure to be taken by Malaysian authority and policy makers to effectively curtail COVID-19 spread in the country.

The present model is formulated to incorporate five control parameters to analyse the effect of different strategies for their implementation on the dynamics of COVID-19 population. However, further studies may take into consideration the development of non-autonomous version of the model to derive the optimal control profiles that are required for each strategy to effectively minimize the spread of COVID-19 population in Malaysia using Pontryagin’s Maximum Principle. Also, cost-effectiveness analysis may be performed to derive the cost-benefits associated with control strategy implementations.

Appendix A: Malaysia COVID-19 data

Table 5 Daily confirmed cases of COVID-19 from March 3 to December 31, 2020