Surface states and breaking down of spin-to-surface locking on a conical topological insulator quantum dot

Abstract

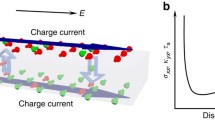
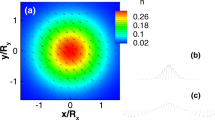
We study a conical topological insulator quantum dot and we show how the cone tip affects the surface states energy spectrum. This is obtained by analytically solving the Dirac equation for these charge carries whose dynamics is restricted to the conical surface. Besides of changing the wave-functions and energy spectrum, the conical tip also yields breakdown of spin-to-surface locking in this geometry.

Graphic abstract

Appendix A: Dirac equation on a conical TI

The derivation of the surface Dirac equation for a conical TI was made following the general method developed in reference [17]. The effective surface Hamiltonian for the spinor ${a} = \displaystyle \begin{bmatrix} a_+\\ a_- \end{bmatrix},$ is specified as

$$\begin{aligned} H_{suf}= \begin{bmatrix} \langle + | H_{\parallel }|+ \rangle &{} \langle + | H_{\parallel }|- \rangle \\ \langle - | H_{\parallel }|+ \rangle &{} \langle - | H_{\parallel }|- \rangle \end{bmatrix} . \end{aligned}$$

(A1)

The approach here is analogue to the procedure in degenerate perturbation theory, as pointed out in [13]. Here, $H_0 = H_{\bot }$ is an unperturbed Hamiltonian and $|\pm \rangle$ are its degenerate eigenstates. To find the spectrum of the perturbed Hamiltonian $H_{tot} = H_0 + H'$, in which $H'= H_{\parallel }$ and $H_{tot}=H_{bulk}$, we have to calculate the matrix elements $\langle \alpha | H' | \beta \rangle , \ (\alpha , \beta = \pm )$ first, and then diagonalize it. Evaluation of the matrix elements leads to

$$\begin{aligned} H_{sur}= \begin{bmatrix} 0 &{} {\mathcal {D}}_+\\ {\mathcal {D}}_- &{} 0 \end{bmatrix} , \end{aligned}$$

(A2)

where

$$\begin{aligned} {\mathcal {D}}_+= & {} \sum _{i=1}^{2} (\eta _i A - \xi _i m_2) \left( \partial _i + \frac{1}{2} [\partial _i \text {ln}(\sqrt{G}] \right) \nonumber \\{} & {} + \frac{1}{2}\partial _i (\eta _i A - \xi _i m_2) , \end{aligned}$$

(A3)

$$\begin{aligned} {\mathcal {D}}_+= & {} \sum _{i=1}^{2} -(\eta _i A - \xi _i m_2)^* \left( \partial _i + \frac{1}{2} [\partial _i \text {ln}(\sqrt{G}] \right) \nonumber \\{} & {} - \frac{1}{2}\partial _i (\eta _i A - \xi _i m_2)^* . \end{aligned}$$

(A4)

In the expressions above,

$$\begin{aligned} \eta _i= & {} \frac{\langle \sqrt{G} \varvec{\theta }^\dagger _+ \sigma ^i \varvec{\theta }_- \rangle }{\langle \sqrt{G} \rangle } , \\ \xi _i= & {} \sum _{j=1}^{2} \frac{\langle \sqrt{G} b^i_j \varvec{\theta }^\dagger _+ \sigma ^i \varvec{\theta }_- \rangle }{\langle \sqrt{G} \rangle } . \end{aligned}$$

All the averages here are taken with respect to the normal coordinate, $\theta$. We have $b^i_j = \partial _j (\varvec{e}_3) \cdot \varvec{e}^i$. Also, $\varvec{\theta }_+$ and $\varvec{\theta }_-$ are defined in equations 15 and 16. So, we can evaluate all necessary terms:

$$\begin{aligned}{} & {} b^1_1 = b^1_2 = b^2_1 = 0, \ \text {while} \ b^2_2 = \frac{\beta }{\alpha r} , \\{} & {} \varvec{\theta }^\dagger _+ \sigma ^1 \varvec{\theta }_- =-1 , \\{} & {} \varvec{\theta }^\dagger _+ \sigma ^2 \varvec{\theta }_- = \frac{i}{\alpha r} . \end{aligned}$$

Since all the averages are over the normal component, and it is reasonable to assume that the $\theta$ coordinate will be practically constant at the surface, we can drop the averages and we get

$$\begin{aligned} \eta _1 = -1 ; \quad \eta _2 = \frac{i}{a r} ; \quad \xi _1 = 0 ; \quad \xi _2 = \frac{i \beta }{\alpha ^2r^2} . \end{aligned}$$

Substituting this quantities on the effective Dirac operator, we arrive in the conical Dirac operator for a topological insulator:

$$\begin{aligned} {\mathcal {D}}_{\pm } = \mp A \left( \frac{\partial }{\partial r} + \frac{1}{2r} \right) + \left( \frac{iA}{\alpha r} + \frac{i\beta }{\alpha ^2 r^2} m_2\right) \frac{\partial }{\partial \phi }\,. \end{aligned}$$

(A5)