Heavy baryon decay widths in the large $N_c$ limit in chiral theory

Abstract

We propose large $N_c$ generalizations for the “diquark” representations of $\hbox {SU}(3)_\mathrm{flav}$ relevant for positive parity heavy baryons, including putative exotic states. Next, within the framework of the Chiral Quark Soliton Model, we calculate heavy baryon masses and decay widths. We show that in the limit of $N_c \rightarrow \infty$ all decay widths vanish, including the widths of exotica. This result is in fact more general than the model itself, as it relies only on the underlying symmetries: i.e. $\hbox {SU}(3)_\mathrm{flav}$ and hedgehog symmetry. Furthermore, using explicit model formulae for the decay constants in the non-realtivistic limit, we show that there is a hierarchy of the decay couplings, which may explain observed pattern of experimental widths.

1 Introduction

Recently the LHCb Collaboration at CERN announced a discovery of five narrow $\varOmega ^0_c$ resonances with masses ranging from 3 to 3.2 GeV [1], that have been later confirmed by BELLE [2]. The widths of these resonances is of the order of a few MeV, with two of them being exceedingly small: $\varGamma (\varOmega _c^0(3050))=0.8\pm 0.2 \pm 0.1$ and $\varGamma (\varOmega _c^0(3119))=1.1 \pm 0.8 \pm 0.4$ MeV. In Refs. [3, 4] we have proposed to interpret these two narrow states as exotic pentaquarks using as a guidance the Chiral Quark Soliton Model [5] ($\chi$QSM – for review see Refs. [6, 7]). Other possible interpretations of these states are summarised in Ref. [8]. The situation here is similar to the light pentaquark state $\varTheta ^+$ [9, 10], which – if it exists – has to be very narrow. Indeed, the evidence for $\varTheta ^+$ that survived until now after the first announcement in 2003 [11,12,13] is the analysis by DIANA Collaboration [14] that requires $\varGamma _{\varTheta ^+} \sim 0.3$ MeV (see also [15]). On theoretical side it has been shown in Ref. [10] that in the non-relativistic limit of the $\chi$QSM the relevant decay coupling of the exotic antidecuplet vanishes identically. This might explain the required smallness of $\varTheta ^+$ decay width.

The nullification of the pertinent decay coupling in the non-relativistic limit occurs only if the rotational sub-leading $1/N_c$ contributions are taken into account [10]. It has been subsequently shown in Ref. [16] that the cancellation of terms that are of different order in $N_c$ is consistent with the large $N_c$ limit if the baryon $SU(3)_\mathrm{flav}$ representations are appropriately enlarged to account for colour neutrality. So despite the fact that formally $\varGamma _{\varTheta ^+}(N_c \rightarrow \infty )=\mathcal{{O}}(1)$ (while the decuplet decay width $\varGamma _{\varDelta }(N_c \rightarrow \infty )=\mathcal{{O}}(1/N_c^2)$) the smallness of the decay width is assured by another small parameter (that, however, has not been analytically defined) related to degree of “relativisticity”.

In Refs. [3, 4, 17] a phenomenological analysis of heavy baryon properties has been performed in the framework of the $\chi$QSM (see also [18,19,20]). It turned out that all decay widths have been very well reproduced [4], also the two narrowest ones of the putative pentaquarks. In the present paper we want to find out whether a suppression mechanism similar to the one discussed above could explain extraordinary small widths of two narrowest $\varOmega _c^0$ states reported by the LHCb (given their interpretation as exotica), or whether the smallness of these widths is a pure numerical coincidence.

In the present paper, extending Ref.  [4], we present an analysis, which shows that there is a hierarchy of the decay constants that indeed suppresses decay widths of heavy pentaquark states, and that degree of this suppression depends on the decay channel. While this result has been to some extent expected from our experience with light quark exotica, the other result that all decay widths of heavy baryons studied here vanish in the large $N_c$ limit (in contrast to the case of $\varTheta ^+$), even if we do not take the non-relativistic limit, comes as a surprise.

The paper is organised as follows. In the next section we briefly recapitulate main features of the $\chi$QSM. Then, in Sect. 3, we show how $\hbox {SU}(3)_\mathrm{flav}$ representations for the light subsystem in heavy baryons have to be generalised to the case of $N_c >3$. This prescription is used in the Appendix to provide the relevant Clebsch–Gordan coefficients needed to compute the decay widths in Sect. 5. To calculate the widths we need mass formulae to calculate the momentum of the outgoing meson, what is done in Sect. 4. We summarise in Sect. 6.

2 Chiral Quark Soliton Model for heavy baryons

The $\chi$QSM is based on an argument of Witten [21,22,23] that in the limit of large number of colors, $N_{c}$ relativistic valence quarks generate chiral mean fields represented by a distortion of a Dirac sea that in turn influence the valence quarks themselves forming a self-organised configuration called a soliton. The soliton configuration corresponds to the solution of the Dirac equation for the constituent quarks (with gluons integrated out) in the mean-field approximation where the mean fields respect so called hedgehog symmetry. Since it is impossible to construct a pseudoscalar field that changes sign under inversion of coordinates, which would be compatible with the $\hbox {SU}(3)_\mathrm{flav}\times \hbox {SO}(3)$ space symmetry, one has to resort to a smaller hedgehog symmetry that, however, leads to the correct baryon spectrum.

Next, rotations of the soliton, both in flavor and configuration spaces, are quantised semiclassically and the collective Hamiltonian is computed. The model predicts rotational baryon spectra that satisfy the following selection rules:

• allowed SU(3) representations must contain states with hypercharge $Y^{\prime }=N_\mathrm{val}/3$,

• the isospin ${ T}^{\prime }$ of the states with $Y^{\prime } =N_\mathrm{val}/3$ is equal the soliton spin J

where $N_\mathrm{val}$ denotes the number of valence quarks.

Rotational energy reads as follows [24,25,26]:

$$\begin{aligned} \mathcal {E}_{\left( p,\, q\right) }^{\mathrm {rot}}= & {} M_{\mathrm {sol}} + \frac{J(J+1)}{2I_{1}} \\&+\;\frac{C_2(p,q)-J(J+1) -3/4\, Y^{\prime \, 2}}{2I_{2}} \end{aligned}$$

(1)

where $C_2$ denotes SU(3) Casimir operator and J stands for the soliton spin. Soliton mass $M_{\mathrm {sol}}$ and moments of inertia $I_{1,2}$ are calculable in terms of relativistic single quark wave functions.

For light baryons $N_\mathrm{val}=N_c$ and the lowest $\hbox {SU}(3)_\mathrm{flav}$ representations allowed by the above selection rules are octet of spin 1/2, decuplet of spin 3/2 and exotic anti-decuplet of spin 1/2. $M_{\mathrm {sol}}$ and $I_{1,2}$ scale like $N_\mathrm{val}$.

Recently we have proposed [17], following Ref. [27], how to generalise the above approach to heavy baryons, by stripping off one valence quark and replacing it by a heavy quark to neutralise the color. In the large $N_c$ limit both systems: light and heavy baryons are described essentially by the same mean field, and the only difference is now that $N_\mathrm{val}=N_c-1$. The lowest allowed SU(3) representations are in this case (as in the quark model) $\overline{\mathbf {3}}$ of spin 0 and to ${\mathbf {6}}$ of spin 1. Therefore, the baryons constructed from such a soliton and a heavy quark form an SU(3) anti-triplet of spin 1/2 and two sextets of spin 1/2 and 3/2 that are subject to a hyper-fine splitting. The first exotic representation is $\overline{\mathbf{15}}$ with spin 0 or 1. However, as can be seen from Eq. (1), the spin 1 soliton is lighter,¹ hence in the following we ignore the one with spin 0. This means that exotic heavy pentaquarks belonging to the $\hbox {SU}(3)_\mathrm{flav}$ $\overline{\mathbf{15}}$ have total spin 1/2 and 3/2. These multiplets are hyperfine split with splitting parameter proportional to $1/m_Q$.

3 Large $N_c$ representations for heavy baryons

For $N_c>3$ we have to generalise $\bar{\mathbf{3}}=(0,1)$,² $\mathbf{6}=(2,0)$ and $\overline{\mathbf{15}}=(1,2)$ to the case of arbitrary (odd) $N_c$ [28,29,30,31]. In this case the $\chi$QSM constraint generalises to $Y'=(N_c-1)/3$. This criterion has to be supplemented by yet another condition, which is usually a requirement that large $N_c$ solitons (and therefore baryons) have the same spin as in the $N_c=3$ case. This means that the pertinent representations have the same number of quark indices $p=p_0$ as for $N_c=3$, but different q. In the quark model language this corresponds to the addition of an antisymmetrised quark pair to a given baryon wave function when we increase $N_c$ by 2. This means that the number of antiquark indices $q_0$ at $N_c=3$ has to be replaced by $q_0+(N_c-3)/2$. Therefore we arrive at the following generalisations:

(2)

with

$$\begin{aligned} q=\frac{N_{c}-3}{2} \end{aligned}$$

(3)

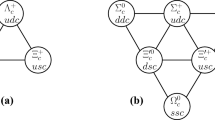
that are illustrated in Fig. 1.

Fig. 1

Large $N_c$ generalizations of weigth diagrams of $\hbox {SU}(3)_\mathrm{flav}$ representations $\bar{\mathbf{3}}$, $\mathbf{6}$ and $\overline{\mathbf{15}}$. Black circles denote physical states that exist for $N_c=3$. Squares denote spurious states that disappear for $N_c=3$. It is understood that these diagrams continue towards negative values of Y. Horizontal dashed (green) lines correspond to $Y'=(N_c-1)/3$

It is now clear that various matrix elements of the irreducible $\hbox {SU}(3)_\mathrm{flav}$ tensor operators will acquire $N_c$ dependence if sandwiched between states belonging to representations (2). In this respect there is no difference between the quark model and the $\chi$QSM. Indeed, it possible to show on general grounds that representation content of the quark model and soliton model coincide for large $N_c$ [32, 33]. The difference appears because due to the hedgehog symmetry the $\chi$QSM provides certain relations between reduced matrix elements in different multiplets, which in the naive quark model are arbitrary.

4 Heavy baryon masses in the Chiral Quark Soliton Model

In the $\chi$QSM the soliton is quantised as a symmetric top and the pertinent mass formula for heavy baryons takes the following form:

$$\begin{aligned} M_B=m_Q+\mathcal {E}_{(p,\, q)}^{\mathrm {rot}} + \delta _B +\varDelta _B^\mathrm{hf} \end{aligned}$$

(4)

where $m_Q$ stands for the heavy quark mass. Rotational soliton energy is given by (1) and mass splittings due to the non-zero strange quark mass $m_s$ are denoted by $\delta _B$, and $\varDelta _B^\mathrm{hf}$ denotes hyperfine splitting which vanishes in a heavy quark limit. These two contributions are not important for the discussion of the large $N_c$ limit.

Mass differences of heavy baryon multiplets are therefore equal to differences of rotational energies:

$$\begin{aligned} \mathcal {E}_\mathbf{6}^{\mathrm {rot}} - \mathcal {E}_{\bar{\mathbf{3}}}^{\mathrm {rot}}= & {} \frac{1}{I_1} \sim \frac{1}{N_c}, \nonumber \\ \mathcal {E}_{\overline{\mathbf{15}}}^{\mathrm {rot}} - \mathcal {E}_{\bar{\mathbf{3}}}^{\mathrm {rot}}= & {} \frac{N_c+1}{4 I_2}+\frac{1}{I_1} \sim N_c^0, \nonumber \\ \mathcal {E}_{\overline{\mathbf{15}}}^{\mathrm {rot}} - \mathcal {E}_{\mathbf{6}}^{\mathrm {rot}}= & {} \frac{N_c+1}{4 I_2} \sim N_c^0. \end{aligned}$$

(5)

We see from Eq. (5) that regular multiplets are degenerate in the large $N_c$ limit, whereas the exotic multiplet, namely $\overline{\mathbf{15}}$, remains heavier by ${\mathcal O}(1)$. Here the situation is identical as in the case of light baryons, where the mass difference between decuplet and octet vanishes for $N_c \rightarrow \infty$, while splitting to the exotic anti-decuplet does not. This behaviour results in the non-vanishing decay width of the exotic $\overline{\mathbf{10}}$, which was the main argument against the consistency of the $\chi$QSM to light baryon exotica [34, 35]. We will see in the following that, despite (5), decay widths of exotic heavy baryons do vanish for large $N_c$.

5 Decay widths

The $\chi$QSM allows to compute strong decay widths that proceed by the soliton transition to another configuration with emission of a pseudoscalar meson $\varphi$. In the present paper following [4] we use strong decay widths of nonexotic and exotic heavy quark baryons (both charm and bottom) computed in an approach proposed many years ago by Adkins, Nappi and Witten [36] and expanded in Ref. [10], which is based on the Goldberger-Treiman relation where strong decay constants are expressed in terms of the axial current couplings (see Ref. [37] for the derivation in the case of heavy baryons). In this case the decay operator can be expressed in terms of the weak axial decay constants³ $a_i$ and meson decay constant $F_{\varphi }$:

$$\begin{aligned} \mathcal {O}^{(8)}_{\varphi }= & {} -\left[ a_{1}D_{\varphi \,i}^{(8)}+a_{2}\,d_{ibc} D_{\varphi \,b}^{(8)}\hat{J}_{c}+a_{3}\frac{1}{\sqrt{3}}D_{\varphi \,8} ^{(8)}\hat{J}_{i}\right] \frac{p_{i}}{2F_{\varphi }}\nonumber \\ \end{aligned}$$

(6)

where $p_{i}$ is the c.m. momentum of the outgoing meson of mass m:

$$\begin{aligned} \left| p_i \right|= & {} p \nonumber \\= & {} \frac{\sqrt{(M_{1}^{2} -(M_{2}+m)^{2})(M_{1}^{2}-(M_{2}-m)^{2})} }{2M_{1}}. \end{aligned}$$

(7)

It is important to note that in the chiral limit where $m \rightarrow 0$ momentum p behaves differently with $N_c$, due to (5), depending on the initial and final flavor representations:

$$\begin{aligned} p_{ \mathbf{6} \rightarrow \overline{\mathbf{3}}} \sim \frac{1}{N_c}, \quad p_{\overline{\mathbf{15}} \rightarrow \mathbf{6}, \overline{\mathbf{3}}} \sim N_c^0. \end{aligned}$$

(8)

This $N_c$ counting is of primary importance for correct determination of the $N_c$ dependence of the decay widths.

The decay width for $B_1 \rightarrow B_2 + \varphi$ is related to the matrix element of $\mathcal {O}^{(8)}_{\varphi }$ squared, summed over the final and averaged over the initial spin and isospin denoted as $\overline{\langle \ldots \rangle ^{2}}$, see the Appendix of Ref. [10] for details of the corresponding calculations:

$$\begin{aligned} \varGamma _{B_{1}\rightarrow B_{2}+\varphi }=\frac{1}{2\pi }\overline{\left\langle B_{2}\left| \mathcal {O}_{\varphi }\right| B_{1}\right\rangle ^{2} }\,\frac{M_{2}}{M_{1}}p. \end{aligned}$$

(9)

Factor $M_{2}/M_{1}$ follows from the heavy baryon chiral perturbation theory, see e.g. Refs. [38, 39]. While it is important for phenomenological applications, it is irrelevant for our discussion as it scales like $N_c^0$.

The final formula for the decay width in terms of axial constants $a_{1,2,3}$ reads as follows:

$$\begin{aligned} \varGamma _{B_{1}\rightarrow B_{2}+\varphi }= & {} \frac{1}{24 \pi }\frac{p^{3} }{F_{\varphi }^{2}}\frac{M_{2}}{M_{1}}G_{\mathcal {R}_{1}\rightarrow \mathcal {R}_{2}}^{2} \frac{\dim \mathcal {R}_{2}}{\dim \mathcal {R}_{1}}\nonumber \\&\times \left[ \begin{array}[c]{cc} {\mathbf{8}} &{} \mathcal {R}_{2}\\ 01 &{} Y^{\prime }S_{2} \end{array} \right| \left. \begin{array}[c]{c} \mathcal {R}_{1}\\ Y^{\prime }S_{1} \end{array} \right] ^{2}\left[ \begin{array}[c]{cc} {\mathbf{8}} &{} \mathcal {R}_{2}\\ Y_{\varphi }T_{\varphi } &{} Y_{2}T_{2} \end{array} \right| \left. \begin{array}[c]{c} \mathcal {R}_{1}\\ Y_{1}T_{1} \end{array} \right] ^{2}\nonumber \\ \end{aligned}$$

(10)

Here $\mathcal {R}_{1,2}$ are the SU(3) representations of the initial and final baryons and [.. .|..] are SU(3) iso-scalar factors. The decay constants $G_{\mathcal {R}_{1}\rightarrow \mathcal {R}_{2}}$ are calculated from the matrix elements of (6) for representations (2) and read as follows:

$$\begin{aligned} G_{\mathbf{6} \rightarrow \overline{\mathbf{3}}}=H_{{\overline{\mathbf{3}}}}= & {} -\tilde{a}_{1}+\frac{1}{2}a_{2} ,\nonumber \\ G_{\overline{\mathbf{15}} \rightarrow \overline{\mathbf{3}}} = G_{\mathbf{\overline{3}}}= & {} -\tilde{a}_{1}-\frac{N_{c}-1}{4} a_{2},\nonumber \\ G_{\overline{\mathbf{15}} \rightarrow \mathbf{6}} = G_\mathbf{6}= & {} -\tilde{a}_{1}-\frac{N_{c}-1}{4}a_{2}-a_{3}. \end{aligned}$$

(11)

In the $\chi$QSM one can define so called non-relativistic (or quark model QM) limit [10, 40, 41] by squeezing the soliton to zero. The easiest way to perform this limit is to use the variational approach, in which one solves the Dirac equation for single quark energy levels in the hedgehog mean field characterised by a variational parameter $r_0$, which is called the soliton size. For the physical solution the value of $r_0$ is determined by the balance of the valence quark contribution that decreases with $r_0$ and the contribution of the appropriately regularised Dirac sea that increases with $r_0$. The QM limit is defined by taking artificially $r_0 \rightarrow 0$. In this limit the valence level reaches its free energy value equal to the constituent mass M. At the same time the contribution of the Dirac sea is approaching zero,⁴ since the soliton energy is evaluated with respect to the unperturbed Dirac sea. In the QM limit parameters $a_i$ can be computed analytically [40, 41]. One has to observe that in the present case the number of valence quarks is $N_c-1$ rather than $N_c$, and therefore the only $N_c$ dependent parameter $a_1$ has to be appropriately rescaled; that is why we have used a “$\tilde{~}$” over $a_1$ [4]. We have [40, 41]:

$$\begin{aligned} -\tilde{a}_{1}{\mathop {\rightarrow }\limits ^\mathrm{QM}} N_{c}+1,\quad a_{2}{\mathop {\rightarrow }\limits ^\mathrm{QM}}4,\quad a_{3}{\mathop {\rightarrow }\limits ^\mathrm{QM}} 2 \end{aligned}$$

(12)

and we get a hierarchy between the decay constants in the QM limit:

$$\begin{aligned} H_{{\overline{\mathbf{3}}}}{\mathop {\rightarrow }\limits ^\mathrm{QM}}N_c+3, \quad G_{\mathbf{\overline{3}}}{\mathop {\rightarrow }\limits ^\mathrm{QM}}2, \quad G_\mathbf{6}{\mathop {\rightarrow }\limits ^\mathrm{QM}} 0. \end{aligned}$$

(13)

By this observation we have argued in Ref. [4] that the decays of exotic $\varOmega _c^0$ resonances should be suppressed with respect to the decays of regular baryons that are driven by the unsuppressed constant $H_{{\overline{\mathbf{3}}}}$.

However, even off the QM limit, where all couplings $H_{{\overline{\mathbf{3}}}}, \;G_{\mathbf{\overline{3}}},\; G_\mathbf{6} \sim N_c$, decays of the exotic $\varOmega _c$’s are suppressed due to the $N_c$ dependence of the pertinent isoscalar factors in Eq.  (10). Indeed, for the energetically allowed decays we have:

$$\begin{aligned} \varGamma _{\varSigma ({\mathbf{6}}_{1})\rightarrow \varLambda (\overline{\mathbf{3} }_{0})+\pi }= & {} \frac{1}{72\pi }\frac{M_{\varLambda (\overline{\mathbf{3}} _{0})}}{M_{\varSigma ({\mathbf{6}}_{1})}}\frac{p^{3}}{F_{\pi }^{2}}\nonumber \\&\times \frac{(N_{c}-1)(N_{c}+3)}{(N_{c}+1)(N_{c}+5)}H_{{\overline{\mathbf{3}}}} ^{2},\nonumber \\ \varGamma _{\varXi ({\mathbf{6}}_{1})\rightarrow \varXi (\overline{\mathbf{3}} _{0})+\pi }= & {} \frac{1}{72\pi }\frac{M_{\varXi (\overline{\mathbf{3}}_{0})} }{M_{\varXi ({\mathbf{6}}_{1})}}\frac{p^{3}}{F_{\pi }^{2}} \nonumber \\&\times \frac{N_{c}^{2}}{(N_{c}+1)(N_{c}+5)}H_{{\overline{\mathbf{3}}}}^{2},\nonumber \\ \varGamma _{\varOmega (\overline{\mathbf{15}}_{1})\rightarrow \varXi (\overline{\mathbf{3}}_{0})+K}= & {} \frac{4}{3\pi }\frac{M_{\varXi (\overline{\mathbf{3}}_{0})}}{M_{\varOmega (\overline{\mathbf{15}}_{1})}}\frac{p^{3}}{F_{K}^{2}}\nonumber \\&\times \frac{G_{{\overline{\mathbf{3}}}}^{2}}{(N_{c} +1)(N_{c}+5)(N_{c}+7)},\nonumber \\ \varGamma _{\varOmega (\overline{\mathbf{15}}_{1})\rightarrow \varOmega ({\mathbf{6}} _{1})+\pi }= & {} \frac{4}{27\pi }\frac{M_{\varOmega ({\mathbf{6}}_{1})}}{M_{\varOmega (\overline{\mathbf{15}}_{1})}}\frac{p^{3}}{F_{\pi }^{2}} \nonumber \\&\times \frac{G_{\mathbf{6}}^{2}}{(N_{c}+1)(N_{c}+7)}\gamma ,\nonumber \\ \varGamma _{\varOmega (\overline{\mathbf{15}}_{1})\rightarrow \varXi ({\mathbf{6}} _{1})+K}= & {} \frac{8}{27\pi }\frac{M_{\varXi ({\mathbf{6}}_{1})}}{M_{\varOmega (\overline{\mathbf{15}}_{1})}}\frac{p^{3}}{F_{K}^{2}}\nonumber \\&\times \frac{G_{\mathbf{6}}^{2}}{(N_{c}+1)^{2}(N_{c}+7)}\gamma . \end{aligned}$$

(14)

For multiplets where the soliton spin J [denoted by a subscript at the representation label in Eq. (14)] is equal to one, hyperfine splittings to a heavy quark result in two spin multiplets 1/2 and 3/2. Factors $\gamma$ take this additional couplings into account:⁵

$$\begin{aligned}&\gamma (1/2\rightarrow 1/2)={2}/{3},\quad \gamma (1/2\rightarrow 3/2)={1} /{3},\nonumber \\&\gamma (3/2\rightarrow 1/2)={1}/{6},\quad \gamma (3/2\rightarrow 3/2)={5}/{6}. \end{aligned}$$

(15)

Armed with explicit formulae for the decay widths (14), for the pertinent couplings (11), for $N_c$ meson momentum dependence (8), and remembering that $F_{\varphi }^2 \sim N_c$, we can compute $N_c$ dependence of the decay widths and, using (13), $N_c$ dependence of the decay widths in the Quark Model limit:

$$\begin{aligned}&\varGamma _{\varSigma ({\mathbf{6}}_{1})\rightarrow \varLambda (\overline{\mathbf{3}}_{0})+\pi } {\mathop {\rightarrow }\limits ^{N_c \rightarrow \infty }} \frac{1}{N_{c}^{2}}{\mathop {\rightarrow }\limits ^\mathrm{QM}}\frac{1}{N_{c}^{2} },\nonumber \\&\varGamma _{\varXi ({\mathbf{6}}_{1})\rightarrow \varXi (\overline{\mathbf{3}} _{0})+\pi } {\mathop {\rightarrow }\limits ^{N_c \rightarrow \infty }} \frac{1}{N_{c}^{2} }{\mathop {\rightarrow }\limits ^\mathrm{QM}}\frac{1}{N_{c}^{2}},\nonumber \\&\varGamma _{\varOmega (\overline{\mathbf{15}}_{1})\rightarrow \varXi (\overline{\mathbf{3}}_{0})+K} {\mathop {\rightarrow }\limits ^{N_c \rightarrow \infty }} \frac{1}{N_{c}^{2}}{\mathop {\rightarrow }\limits ^\mathrm{QM}} \frac{1}{N_{c}^{4}},\nonumber \\&\varGamma _{\varOmega (\overline{\mathbf{15}}_{1})\rightarrow \varOmega ({\mathbf{6}}_{1})+\pi } {\mathop {\rightarrow }\limits ^{N_c \rightarrow \infty }} \frac{1}{N_{c}}{\mathop {\rightarrow }\limits ^\mathrm{QM}} 0,\nonumber \\&\varGamma _{\varOmega (\overline{\mathbf{15}}_{1})\rightarrow \varXi ({\mathbf{6}} _{1})+K}{\mathop {\rightarrow }\limits ^{N_c \rightarrow \infty }} \frac{1}{N_{c}^{2} }{\mathop {\rightarrow }\limits ^\mathrm{QM}} 0. \end{aligned}$$

(16)

Equations (16) show that all widths relevant for heavy baryon decays, including exotica, vanish for $N_c \rightarrow \infty$. This result is quite obvious for regular baryons that are degenerate in this limit (see Eqs. (5), (8)), and the quadratic dependence on $1/N_c$ is the same as in the case of e.g. $\varDelta$ decay. It is however surprising that for $N_c \rightarrow \infty$ exotic states that are not degenerate with the ground state heavy baryons (see again Eqs. (5) and (8)), have nevertheless decay widths that tend to zero in contrast with the decay width of the putative light pentaquark $\varTheta ^+$. For a decay linking baryons of the same isospin the suppression power is weaker by one. In the Quark Model limit the decay widths of exotica are, however, further suppressed. This is an interesting situation not known from the light baryons and it deserves more detailed studies.

6 Summary

Prompted by the pentaquark assignment of two narrowest $\varOmega _c^0$ states reported recently by the LHCb Collaboration we have studied the large $N_c$ limit of the decay widths of heavy quark baryons within the Chiral Quark Soliton Model. We have calculated all energetically allowed strong decays of the ground state $\hbox {SU}(3)_\mathrm{flav}$ sextet and of the putative pentaquark $\varOmega _c^0$’s. To this end we have used heavy baryon chiral perturbation theory and the Glodberger-Treiman relation for heavy baryons.

We have proposed a natural enlargement of the pertinent $\hbox {SU}(3)_\mathrm{flav}$ representations for $N_c \rightarrow \infty$ and calculated the relevant matrix elements obtaining analytical results for arbitrary (odd) $N_c$. This required to calculate SU(3) Clebsch–Gordan coefficients for large representations (2). The relevant technique has been briefly discussed in the Appendix.

The main result is that all decay widths studied in this paper vanish in the limit of large $N_c$, either as $(1/N_c)^2$ or as $1/N_c$. This is true also for decays of exotica, for which the phase space momentum of the outgoing meson does not vanish in this limit.

Furthermore we have investigated the large $N_c$ and the Quark Model limits of the decay constants. In this limit there is a hierarchy of the decay couplings (16): decays of regular baryons are not suppressed, pentaquark decay coupling to anti-triplet is suppressed by $1/N_c$, whereas for the sextet the pertinent coupling vanishes.

Appendix

In this appendix we briefly sketch techniques used to calculate SU(3) Clebsch–Gordan coefficients for large representations (2). The following Clebsch–Gordan series are relevant for the decay widths discussed in this paper:

$$\begin{aligned} (1,1)\otimes \overset{``{\overline{\mathbf{3}}}\hbox {''}}{\overbrace{(0,q+1)}}= & {} \overset{``\overline{\mathbf{15}}\hbox {''}}{\underset{Y_{0}+1,1/2}{\underbrace{\overbrace{(1,q+2)}}}}\oplus \underset{Y_{0},1}{\overset{``{} \mathbf{6} \hbox {''}}{\underbrace{\overbrace{(2,q)}}}}\oplus \,\underset{Y_{0},0}{\overset{``{\overline{\mathbf{3}}}\hbox {''}}{\underbrace{\overbrace{(0,q+1)}}}} \nonumber \\&\oplus \overset{\text {spurious}}{\underset{Y_{0}-1,1/2}{\underbrace{\overbrace{(1,q-1)}}}}\; , \nonumber \\ (1,1)\otimes \overset{``{} \mathbf{6}\hbox {''}}{\overbrace{(2,q)}}= & {} \underset{Y_{0}+1,3/2}{\overset{``{} \mathbf{24}\hbox {''}}{\underbrace{\overbrace{(3,q+1)}}} }\oplus \overset{``\overline{\mathbf{15}}\hbox {''}}{\underset{Y_{0}+1,1/2}{\underbrace{\overbrace{(1,q+2)}}}}\nonumber \\&\oplus \overset{\text {spurious}_{1}}{\underset{Y_{0},2}{\overbrace{\underbrace{(4,q-1)}}}}\oplus 2\,\underset{Y_{0},1}{\overset{``{} \mathbf{6} \hbox {''}}{\underbrace{\overbrace{(2,q)}}}}\oplus \underset{Y_{0},0}{\overset{``{\overline{\mathbf{3}}}\hbox {''}}{\underbrace{\overbrace{(0,q+1)}}}}\nonumber \\&\oplus \overset{\text {spurious}_{2}}{\underset{Y_{0}-1,3/2}{\underbrace{\overbrace{(3,q-2)}}}}\oplus \overset{\text {spurious}_{3}}{\underset{Y_{0}-1,1/2}{\underbrace{\overbrace{(1,q-1)}}}}\,. \end{aligned}$$

(17)

Labels in quotation marks above representation labels (p, q) correspond to the $N_c=3$ limit for these representations, representations that are not present for $N_c=3$ are denoted as spurious. Labels below correspond to the hypercharge and isospin of the highest weight in a given representation, with $Y_0=(N_c-1)/3$.

The construction proceeds by starting from the highest weight of the largest representation in (17), for which the SU(3) Clebsch–Gordan coefficient is 1. Then we apply lowering I-spin, U-spin and V-spin operators to construct the remaining states in this representation. For explicit form of these operators see e.g. [42]. Whenever we encounter a state for which an orthogonal state exists, we assign it either to another isospin multiplet in the same representation, or to some lower dimensional representation choosing the phases according to de Swart convention [43]. To calculate the decay widths we need to construct only $``\overline{\mathbf{15}}\hbox {''}$ and $``{} \mathbf{6}\hbox {''}$ in the first series and $``\overline{\mathbf{15}}\hbox {''}$ in the second. All Clebsch–Gordan coefficients have been checked numerically for a few fixed values of $N_c$ with the numerical code of Ref. [44].