Spherically symmetric black holes with electric and magnetic charge in extended gravity: physical properties, causal structure, and stability analysis in Einstein’s and Jordan’s frames

Abstract

Novel static black hole solutions with electric and magnetic charges are derived for the class of modified gravities: $f({{{\mathcal {R}}}})={{{\mathcal {R}}}}+2\beta \sqrt{{{\mathcal {R}}}}$, with or without a cosmological constant. The new black holes behave asymptotically as flat or (A)dS space-times with a dynamical value of the Ricci scalar given by $R=\frac{1}{r^2}$ and $R=\frac{8r^2\Lambda +1}{r^2}$, respectively. They are characterized by three parameters, namely their mass and electric and magnetic charges, and constitute black hole solutions different from those in Einstein’s general relativity. Their singularities are studied by obtaining the Kretschmann scalar and Ricci tensor, which shows a dependence on the parameter $\beta$ that is not permitted to be zero. A conformal transformation is used to display the black holes in Einstein’s frame and check if its physical behavior is changed w.r.t. the Jordan one. To this end, thermodynamical quantities, as the entropy, Hawking temperature, quasi-local energy, and the Gibbs free energy are calculated to investigate the thermal stability of the solutions. Also, the casual structure of the new black holes is studied, and a stability analysis is performed in both frames using the odd perturbations technique and the study of the geodesic deviation. It is concluded that, generically, there is coincidence of the physical properties of the novel black holes in both frames, although this turns not to be the case for the Hawking temperature.

1 Introduction

The discovery of gravitational waves (GW) has shed light on a new possibility to probe the laws of physics in strong gravitational fields [1]. General relativity (GR) has been confirmed to a very good precision on weak gravitational field backgrounds [2]; however, the precise form of the anticipated, necessary modification of GR to deal with strong gravitational fields is not confirmed yet, although different possibilities have been proposed. The discovery of GW definitely provides an excellent chance to test those modified gravity theories in the strong gravitational fields of black hole solutions [3] and neutron stars [4].

The simplest generalizations of GR are the $f({{\mathcal {R}}})$ gravitational theories, whose Lagrangian involves nonlinear terms in ${{\mathcal {R}}}$. A simple possibility is power-law gravity, described by a Lagrangian of the form

$$\begin{aligned} f({{\mathcal {R}}}) = {{\mathcal {R}}}+\frac{{{\mathcal {R}}}^n}{6m^2}, \end{aligned}$$

where n is an arbitrary number and with $m^2$ being a positive mass squared. The term ${{\mathcal {R}}}^2$ has a natural interpretation as corresponding to the lowest order quantum perturbative additions to classical gravity, and it is, at the same time, responsible for cosmic inflation in the early Universe. In addition, this term should be seriously considered when dealing with local objects on the background of a strong gravitational field. In relation with this, many research papers have been devoted to the study of static spherically symmetric black hole solutions, as e.g. [5,6,7,8,9,10,11,12,13,14], and neutron stars solutions [15,16,17,18,19,20,21,22,23,24,25,26,27,28]. It is also known that $f({{\mathcal {R}}})$ theories can be matched to Brans–Dicke theories [29], which involve a scalar and a potential of gravitational origin [30, 31]. Alike as for black holes, in Brans-Dicke theories having a potential with positive mass squared there is a “no-hair (B theorem)”, which prevents the appearance of non-trivial scalar hair [32, 33], and this theorem also forbids the presence of hairy black hole solutions in the ${{\mathcal {R}}}^2$ model [6, 7, 12, 13]. A number of black holes have been already obtained in the framework of $f({{\mathcal {R}}})$ theories [6, 34,35,36,37,38,39,40,41,42,43,44], their physical properties having been discussed in, e.g., [45,46,47,48].

The observation of the mathematical similarity between gravitational and electromagnetic fields goes back at least to the eighteenth century, when Coulomb constructed his inverse square law to formulate the force between two charges at a distance r [49]. Coulomb’s law is, in this sense, a complete analogue of the gravitational law [50] for the force acting on two masses separated by the same distance. The similarity between this expression for the two forces led scientists to conjecture that the gravitational force exerted by the sun on the planets could be accompanied by a magnetic force leading to the precession of their orbits and, thence, they would investigate from this standpoint the discrepancy found by Newton in the precession of Mercury’s orbit. In fact, Mercury’s perihelion precession was definitely explained by Einstein’s GR, sometime after this similarity between gravitational and electromagnetic fields had been exploited, in some regimes. Moreover, it is known that gravitation involves a gravitomagnetic field because of the mass current [51,52,53,54]. Additionally, Einstein GR forecasts a gravitomagnetic field because of the proper rotation of the Sun that effects the planetary orbits [55,56,57]. Those are well-known facts. The aim of the present paper is to construct brand new black hole solutions,¹ possessing electric and magnetic charge, within the family of $f({{\mathcal {R}}})$ modified gravities, to describe them in both the Jordan and the Einstein frames, and to study a number of their physical properties, by calculating associated thermodynamical quantities. Moreover, we will study their causal structure and perform a detailed stability analysis by using odd perturbation techniques and the study of the geodesic deviation.

The paper is organized as follows. In Sect. 2 a brief introduction to the theory of Maxwell-$f({{\mathcal {R}}})$ gravity is given. In Sect. 3, restricting to spherical symmetry, an exact solution of the field equations of the Maxwell-$f({{\mathcal {R}}})$ theory is obtained. In Sect. 4, the same derivation is performed for the case of the Maxwell-$f({{\mathcal {R}}})$ theory involving a cosmological constant, and a new black hole solution is constructed, which behaves asymptotically as AdS or dS space. In Sect. 5, the characteristic properties of the found black holes are analyzed in detail. In Sect. 6, by using conformal transformation, we derive the black hole solutions in the Einstein frame. In Sect. 7, basic thermodynamical quantities, such as the entropy, quasi-local energy, the Hawking temperature, and the Gibbs energy are calculated in both the Einstein and the Jordan frames. These calculations show that (with the sole exception of the Hawking temperature) the physical behavior of the black holes obtained do not change generically in going from one to the other frame. In Sect. 8 we study the linear stability of the black hole solutions derived in Sects. 3, 4 and 6, by using the odd perturbations technique. In addition, in Sect. 9, the stability conditions when considering geodesic motion are derived. In Sec. we discuss the causal structure of our solution obtained in Sect. 3. Finally, in Sect. 11 we present a summary of the main results of this work, draw some compelling conclusions, and discuss some ideas for future work.

2 Brief note on the Maxwell–$f({{\mathcal {R}}})$ theory

The theory of $f({{\mathcal {R}}})$ gravity is an extension of Einstein’s GR, first discussed in [59,60,61,62,63,64,65,66]. The Lagrangian of this theory is

$$\begin{aligned} {\mathop {\mathcal { L}}}:= {\mathop {\mathcal { L}}}_g+{\mathop {\mathcal { L}}}_{E.M.}, \end{aligned}$$

(1)

its gravitational term being ${\mathop {\mathcal { L}}}_g$, which is given by

$$\begin{aligned} {\mathop {\mathcal { L}}}_g:=\frac{1}{2\kappa } \int d^4x \sqrt{-g} (f({{\mathcal {R}}})-\Lambda ), \end{aligned}$$

(2)

with $\Lambda$ the cosmological constant, ${{\mathcal {R}}}$ the Ricci scalar, $\kappa$ the gravitational constant, g the determinant of the metric, and $f({{\mathcal {R}}})$ an analytic function. Here, we have defined the energy-momentum as ${\mathop {\mathcal {L}}}_{_{_{ E.M.}}}$, the Lagrangian of the electromagnetic field, which is given by

$$\begin{aligned} {\mathop {\mathcal {L}}}_{_{_{ E.M.}}}:=-\frac{1}{2}F^{2}, \end{aligned}$$

(3)

where $F^2=F_{\mu \nu }F^{\mu \nu }$ and $F_{\mu \nu } =2\xi _{[\mu , \nu ]}$, with $\xi _\mu$ being the gauge potential 1-form, while the comma denotes ordinary differentiation² [67].

Performing the variations of the Lagrangian of Eq. (1) w.r.t. the metric tensor $g_{\mu \nu }$ and w.r.t. the strength tensor F, respectively, one gets the field equations of the Maxwell-$f({{\mathcal {R}}})$ theory, in the form [68]

$$\begin{aligned}&\zeta _{\mu \nu }={{\mathcal {R}}}_{\mu \nu } f_{{\mathcal {R}}}-\frac{1}{2}g_{\mu \nu }f({{\mathcal {R}}})-2g_{\mu \nu }\Lambda \nonumber \\&\quad \qquad +g_{\mu \nu } \Box f_{{\mathcal {R}}}-\nabla _\mu \nabla _\nu f_{{\mathcal {R}}}-8\pi T_{\mu \nu }\equiv 0,\end{aligned}$$

(4)

$$\begin{aligned}&\partial _\nu \left( \sqrt{-g} {\text {F}}^{\mu \nu } \right) =0, \end{aligned}$$

(5)

where ${{\mathcal {R}}}_{\mu \nu }$ is the Ricci tensor³ and $\Box$ is the d’Alembertian operator, defined as $\Box = \nabla _\alpha \nabla ^\alpha$, where $\nabla _\alpha A^\beta$ is the covariant derivative of the vector $A^\beta$, and ${\displaystyle f_{{\mathcal {R}}}=\frac{df({{\mathcal {R}}})}{d{{\mathcal {R}}}}}$. Here, we define the energy-momentum tensor, $T_{\mu \nu }$, as

$$\begin{aligned} T_{\mu \nu }:=\frac{1}{4\pi }\left( { \text {g}}_{\rho \sigma }{{\text {F}}_\nu {}^\rho }{{{\text {F}}}_\mu }^{\sigma }-\displaystyle {1 \over 4} {\text {g}}_{\mu \nu } F^{2}\right) . \end{aligned}$$

(6)

Taking the trace in Eq. (4), one gets

$$\begin{aligned} \zeta ={{\mathcal {R}}}f_{{\mathcal {R}}}-2f({{\mathcal {R}}})-8\Lambda +3\Box f_{{\mathcal {R}}}=0. \end{aligned}$$

(7)

In the following, we are going to assume a particular form for the field Eq. (4), with and without a cosmological constant, in order to be able to derive exact charged solutions asymptotically behaving as flat, respectively AdS/dS space-times.

3 Black hole solutions with magnetic and electric charge

In this section we obtain a charged black hole solution for the model

$$\begin{aligned} f({{\mathcal {R}}})={{\mathcal {R}}}+2\beta \sqrt{{{\mathcal {R}}}}. \end{aligned}$$

(8)

To achieve this, we introduce the following spherically symmetric ansatz⁴

$$\begin{aligned} ds^2=-w(r)dt^2+\frac{dr^2}{w(r)}+r^2(d\theta ^2+\sin ^2d\phi ^2). \end{aligned}$$

(9)

The Ricci scalar of the line-element (9) is given by

$$\begin{aligned} {{\mathcal {R}}}=\frac{2-r^2w''-4rw'-2w}{r^2}, \end{aligned}$$

(10)

where $w\equiv w(r)$, $w'\equiv \frac{dw(r)}{dr}$, and $w''\equiv \frac{d^2w(r)}{dr^2}$. Using Eqs. (9) in (4), (5) and (7), after using Eq. (10) we get a system of fourth order differential equations which are listed in Appendix A. The off-diagonal components of these system, $( A\cdot 2)$, $(A\cdot 4)$ and $( A\cdot 5)$, can be solved to determine the unknown functions n, p, s, and k. Substituting the values of these function into the diagonal components, as well as into the trace field equation, we get the following exact solution

$$\begin{aligned}&w(r)=\frac{1}{2}+\frac{c_1}{ r}+\frac{{q_{_E}}{}^2+{q_{_M}}{}^2}{ r^2}, \qquad q=\frac{{q_{_E}}}{r}, \qquad n=c_2 \theta , \nonumber \\&s=c_2r, \qquad p=c_3 r, \qquad k=c_4 \theta -{q_{_M}}\cos \theta , \end{aligned}$$

(11)

where the $c_i$, $i=1\cdots 4$, are constant, and $q_{_E}$ and $q_{_M}$ are other constants related to the electric and magnetic charge, respectively. The analytic solution (11) satisfies the system of differential equations presented in Appendix A, including the trace of the field equations, provided that $c_1=\frac{1}{3\beta }$. Using Eq. (10) we get the Ricci scalar, in the form

$$\begin{aligned} {{\mathcal {R}}}=\frac{1}{r^2}, \end{aligned}$$

(12)

which provides also a consistency check for the whole procedure. The metric of the solution (11) takes the form

$$\begin{aligned} ds^2= & {} -\left( \frac{1}{2}+\frac{1}{3\beta r}+\frac{{{\mathcal {K}}}^2}{r^2}\right) dt^{2}\nonumber \\&+\left( \frac{1}{2}+\frac{1}{3\beta r}+\frac{{{\mathcal {K}}}^2}{ r^2}\right) ^{-1}dr^2+r^2d\Omega ^2, \end{aligned}$$

(13)

where we have set ${q_{_E}}{}^2+{q_{_M}}{}^2={{\mathcal {K}}}^2$. Equation (13) behaves asymptotically as a flat space-time. Solution (11) coincides with that obtained in [69] when ${{\mathcal {K}}}^2=0$, i.e. $q_E=q_M=0$. Also, the solution obtained (13) corresponds to the spherically symmetric space-time in $f({{\mathcal {R}}})$ gravitational theories, and differs from the corresponding one in [58] by the more general expression of the 1-form gauge potential (A. 9) and by the parameter ${{\mathcal {K}}}$ that couples to electric and magnetic fields.

4 Analytic AdS/dS charged solutions

To derive a charged black hole solution that behaves asymptotically as AdS/dS we assume f(R) to have the form

$$\begin{aligned} f({{\mathcal {R}}})={{\mathcal {R}}}+2\beta \sqrt{{{\mathcal {R}}}-8\Lambda }. \end{aligned}$$

(14)

Applying the ansatz (9) to the field Eqs. (4), (5), and (7), after using (10), we get a system of fourth order differential equations listed in Appendix B.

Using the previous procedure, namely solving the off-diagonal components and substituting their values in the diagonal ones, we get the following exact solution

$$\begin{aligned}&w(r)=\frac{1}{2}-\frac{2r^2\Lambda }{3}+\frac{1}{3\beta r}+\frac{{q_{_E}}{}^2+{q_{_M}}{}^2}{ r^2}, \qquad q=\frac{{q_{_E}}}{r}, \nonumber \\&n=c_2 \theta , \qquad s=c_2r, \qquad p=c_3 r, \nonumber \\&k=c_4 \theta -{q_{_M}}\cos \theta . \end{aligned}$$

(15)

Introducing Eq. (15) into (10), we get the Ricci scalar, in the form

$$\begin{aligned} {{\mathcal {R}}}=\frac{8r^2\Lambda +1}{r^2}. \end{aligned}$$

(16)

The metric of the above solution reads

$$\begin{aligned} ds^2= & {} -\left( \frac{1}{2}-\frac{2r^2\Lambda }{3}+\frac{1}{3\beta r}+\frac{{q_{_E}}{}^2+{q_{_M}}{}^2}{r^2}\right) dt^{2}\nonumber \\&+\left( \frac{1}{2}-\frac{2r^2\Lambda }{3}+\frac{1}{3\beta r}+\frac{{q_{_E}}{}^2+{q_{_M}}{}^2}{ r^2}\right) ^{-1}dr^2+r^2d\Omega ^2\, ,\nonumber \\ \end{aligned}$$

(17)

and behaves asymptotically as AdS/dS space-time. The solution (15) is different from the one derived in [69], owing to the same reason already discussed for the solution (11).

5 Physical significance of the new black holes

The metric of the solution (11) can be rewritten as

$$\begin{aligned} ds^2= & {} -\left( \frac{1}{2}-\frac{m}{ r}+\frac{{{\mathcal {K}}}^2}{ r^2}\right) dt^{2}\nonumber \\&+\left( \frac{1}{2}-\frac{m}{r}+\frac{{{\mathcal {K}}}^2}{ r^2}\right) ^{-1}dr^2+r^2d\Omega ^2\;, \qquad \text {where}\nonumber \\ m= & {} -c_1=-\frac{1}{3\beta }. \end{aligned}$$

(18)

Equation (18) indicates that the dimensional parameter $\beta$ cannot vanish. Moreover, Eq. (18) shows that the line-element coincides with the Reissner-Nordström space-time when ${{\mathcal {K}}}=q_{_E}$ and $q_{_M}=0$.

The line-element of the solution (15) can be written as

$$\begin{aligned} ds^2= & {} \left( \frac{1}{2}-\frac{2r^2\Lambda }{3}-\frac{m}{r}+\frac{{{\mathcal {K}}}^2}{ r^2}\right) dt^{2}\nonumber \\&-\left( \frac{1}{2}-\frac{2r^2\Lambda }{3}-\frac{m}{r}+\frac{{{\mathcal {K}}}^2}{ r^2}\right) ^{-1}dr^2-r^2d\Omega ^2\;, \quad \text {where, again}\nonumber \\ m= & {} -c_1=-\frac{1}{3\beta }, \end{aligned}$$

(19)

which tells us that the line-element (19) does behave asymptotically as AdS/dS and that it coincides with the Reissner-Nordström space-time when ${{\mathcal {K}}}=q_{_E}$ and $q_{_M}=0$. Equations (18) and (19) show, in a clear way, that the dimensional parameter $\beta$ cannot vanish.

Let us study now the regularity of the solutions (11) and (15), when $w(r)=0$ [70]. For the solution (11), we evaluate the scalar invariants and get

$$\begin{aligned}&{{\mathcal {R}}}^{\mu \nu \lambda \rho }{{\mathcal {R}}}_{\mu \nu \lambda \rho }= \frac{4r^2-4\beta r^3+3r^4\beta ^2+{{\mathcal {K}}}^2[48r \beta -12r^2\beta ^2+168\beta ^2] +336\beta q_{_M}^2q_{_M}^2}{3\beta ^2r^8}, \nonumber \\&{{\mathcal {R}}}^{\mu \nu }{{\mathcal {R}}}_{\mu \nu } =\frac{r^4+{{\mathcal {K}}}^2[4r^2+8{{\mathcal {K}}}^2]}{2r^8}, \qquad \qquad {{\mathcal {R}}}= \frac{1}{r^2}, \end{aligned}$$

(20)

where ${{\mathcal {R}}}^{\mu \nu \lambda \rho }{{\mathcal {R}}}_{\mu \nu \lambda \rho }$, ${{\mathcal {R}}}^{\mu \nu }{{\mathcal {R}}}_{\mu \nu }$, and ${{\mathcal {R}}}$ are the Kretschmann scalars, the Ricci tensor square, and the Ricci scalar, respectively. Equation (20) show that, at $r=0$, the solutions develop a true singularity and that the dimensional parameter $\beta \ne 0$. Also, Eq. (11), as well as Eq. (13), point out to the fact that the dimensional parameter $\beta$ cannot be zero, which assures that the solution (11) cannot possibly reduce to one in GR. In other words, this solution is a genuinely new one, an exact, charged solution in the class of $f({{\mathcal {R}}})$ modified gravity theories.

Using Eq. (15), we get the scalar invariants in the form

$$\begin{aligned}&{{\mathcal {R}}}^{\mu \nu \lambda \rho }{{\mathcal {R}}}_{\mu \nu \lambda \rho } =\frac{4r^2-4\beta r^3+3r^4\beta ^2+{{\mathcal {K}}}^2[48r \beta -12r^2\beta ^2+168\beta ^2]+336\beta q_{_M}^2q_{_M}^2+8r^6\beta ^2\Lambda [4r^2\Lambda +1]}{3\beta ^2r^8},\nonumber \\&{{\mathcal {R}}}^{\mu \nu }{{\mathcal {R}}}_{\mu \nu } =\frac{r^4+{{\mathcal {K}}}^2[4r^2+8{{\mathcal {K}}}^2]+8r^6\beta ^2\Lambda [4r^2\Lambda +1]}{2r^8}, {{\mathcal {R}}} =\frac{8r^2\Lambda +1}{r^2}. \end{aligned}$$

(21)

The same considerations already done for the solution (11) can also be applied now to the solution (15), what will insure also that (15) is a brand new, charged solution constructed in the class of $f({{\mathcal {R}}})$ gravities, and that it cannot possibly be reduced to a GR solution.

6 Charged black hole solutions in the Einstein frame

In this section we will construct charged black holes in the Einstein frame. We thus start with a brief description of f(R) theories in the Einstein frame. It is rather well-know that f(R) gravitational theories can be rewritten under the form of a Brans-Dicke theory, by involving a subsidiary field, $\psi$, through a non-minimal coupling term, as

$$\begin{aligned} {{\mathcal {L}}}:= & {} \int d^4x \sqrt{-g}\, \left[ \frac{1}{2\kappa } f_\psi (\psi )(R-\Lambda )\right. \nonumber \\&\left. -\left( \frac{\psi f_\psi (\psi )-f(\psi )}{2\kappa }\right) \right] +{\mathop {\mathcal { L}}}_{_{E.M.}}, \end{aligned}$$

(22)

where $f_\psi (\psi )=\frac{f(\psi )}{d \psi }$ and ${\mathop {\mathcal { L}}}_{_{E.M.}}$ is the Lagrangian of the electromagnetic field, given by Eq. (3). Variation of Eq. (22) w.r.t. $\psi$ gives $f_{\psi \psi }(R-\Lambda -\psi )=0$. For $f_{\psi \psi }\ne 0$, one can obtain $\psi =R-\Lambda$ and the above action returns back to the one of Eq. (1). This means that the field equations produced by the action (22) exactly coincide with those previously derived from the Lagrangian (1), namely (4) and (5).

When choosing $\sigma =f_{\psi }(\psi )$, the Lagrangian (22) is termed as a Brans–Dicke’s like theory with a non-minimal coupling term $\sigma R$ and a scalaron potential $V(\sigma )$. It is well-know that the non-minimal coupling term can be eliminated from the Jordan frame, by moving to the Einstein frame, using the following conformal transformation

$$\begin{aligned} g_{\mu \nu } \rightarrow {{\bar{g}}}_{\mu \nu }(x)=\Omega ^2(x) g_{\mu \nu }(x), \end{aligned}$$

(23)

where the space-time conformal factor has been chosen as $\Omega ^2(x) =f_{{\mathcal {R}}}$, what demands that $f_{{\mathcal {R}}} > 0$ [71, 72]. From the transformation (23), one can show that the Ricci scalar transforms as $R\rightarrow \bar{R}$. Using now the canonical scalar field

$$\begin{aligned} \psi =\sqrt{\frac{6}{\kappa }}\, \ln \Omega =\sqrt{\frac{3}{2\kappa }}\, \ln f_{{\mathcal {R}}}, \end{aligned}$$

(24)

and from the conformal transformation (23), the Lagrangian (22) converts into a scalar-tensor theory in the Einstein frame, as

$$\begin{aligned} {\mathop {\mathcal { L}_E}}:= & {} \int d^4x \sqrt{-{{\bar{g}}}} \left[ \frac{1}{2\kappa }({\bar{{\mathcal {R}}}} -\Lambda )\right. \nonumber \\&\left. -\frac{1}{2}{{{\bar{g}}}}^{\mu \nu }\partial _\mu \psi \partial _\nu \psi -V(\psi )\right] +\mathcal {L}_{_{E.M.}}, \end{aligned}$$

(25)

where

$$\begin{aligned} V_E(\psi )=\displaystyle \frac{{{\mathcal {R}}}f_{{\mathcal {R}}}-f}{2\kappa {f_{{\mathcal {R}}}}^2}=\frac{V(\psi )}{f_R^2}, \end{aligned}$$

(26)

is the potential of the canonical scalar field $\psi$. The potential $V_E(\psi )$ can be rewritten in terms of $\psi$ by using the inverse relation $f_{{\mathcal {R}}}=e^{ \sqrt{2\kappa /3}\,\psi }$. Performing the conformal transformation (23), the energy–momentum tensor converts into [72,73,74,75,76,77]

$$\begin{aligned} T_{\mu \nu } \rightarrow \bar{T}_{\mu \nu }=\Omega (x)^{-2} T_{\mu \nu }. \end{aligned}$$

(27)

In the following, we are going to apply the conformal transformation (23) to the space-time metric (18), i.e. $d\bar{s}_E^2=\Omega ^2 ds_J^2$, where the conformal factor of the f(R) gravity (8) is given by

$$\begin{aligned} \Omega ^2=f_R=1+r\beta . \end{aligned}$$

(28)

The relation between the scalar field $\Omega$ and the radial coordinate r is plotted in Fig. 1. Finally, using Eq. (26), the potential of this model reads

$$\begin{aligned}&V(r)=-\frac{\beta }{2\kappa ^2r(1+\beta r)^2},\nonumber \\&\Rightarrow V(\Omega )= \frac{\beta ^{2}}{2\kappa ^2\Omega ^4(1-\Omega ^2)}. \end{aligned}$$

(29)

Equation (29) is plotted in Fig. 2.

Fig. 1

Schematic plot of the radial coordinate r versus the scalar field $\Omega$

Fig. 2

Schematic plot of the scalar field $\Omega$ versus the potential V

Thus, we can write the Einstein frame metric as

$$\begin{aligned} d\bar{s}_E^2= & {} \Omega ^2\left[ -w(r) dt^2+\frac{dr^2}{w(r)}+r^2 \left( d\theta ^2+\sin ^2 \theta d\phi ^2\right) \right] ,\nonumber \\= & {} -\bar{w}(\bar{r}) dt^2+\frac{d\bar{r}^2}{\bar{w_1}(\bar{r})}+\bar{r}^2 \left( d\theta ^2+\sin ^2 \theta d\phi ^2\right) , \end{aligned}$$

(30)

where

$$\begin{aligned} \bar{r}= & {} \Omega (r)r, \qquad \bar{w}(\bar{r})=w(r(\bar{r}))=\Omega ^2(\bar{r})w(\bar{r}), \nonumber \\ \bar{w}_1(\bar{r})= & {} w_1(r(\bar{r}))=\frac{\Omega ^2(\bar{r}) [x^2(\bar{r})+12x(\bar{r})+144]^2}{16x(\bar{r})[x^2(\bar{r})+6x(\bar{r})+144]}\,, \quad \text {where} \nonumber \\ x(\bar{r})= & {} \Bigg \{12\Big [9\beta \bar{r}+\sqrt{81\beta ^2\bar{r}^2-12}\Big ]\Bigg \}^{2/3}. \end{aligned}$$

(31)

Equation (31) shows that the solutions (11) and (15) have been deformed due to the conformal transformation (23) and that the dimensional parameter $\beta$ must satisfy $\beta >\frac{2}{3\sqrt{3}\bar{r}}$. Is this deformation effect conveying the physics in both the Jordan and the Einstein frames? We will answer this question in the next section.

7 Black hole thermodynamics in the Jordan frame

The Hawking temperature is usually defined as [78,79,80,81]

$$\begin{aligned} T_+ = \frac{w'(r_+)}{4\pi }, \end{aligned}$$

(32)

where the event horizon $r = r_+$ is the largest positive root of $w(r_+) = 0$ that satisfies $w'(r_+)\ne 0$. In the framework of $f({{\mathcal {R}}})$ gravity, the entropy is given by [82, 83]

$$\begin{aligned} S(r_+)=\frac{1}{4}Af_{{{\mathcal {R}}}}(r_+), \end{aligned}$$

(33)

with A being the area of the event horizon. The quasi-local energy, in the framework of $f({{\mathcal {R}}})$ gravity is defined as [82, 83]

$$\begin{aligned} E(r_+)= & {} \frac{1}{4}\displaystyle {\int }\Bigg [2f_{{{\mathcal {R}}}}(r_+)+r_+{}^2\Big \{f({{\mathcal {R}}} (r_+))\nonumber \\&-{{\mathcal {R}}}(r_+)f_{{{\mathcal {R}}}}(r_+)\Big \}\Bigg ]dr_+. \end{aligned}$$

(34)

The constraint $w(r_+) = 0$ yields

$$\begin{aligned} {r_+}_{{}_{{}_{{}_{{}_{\tiny Eq. (11)}}}}}= & {} -\frac{1}{3\beta }\left[ 1+\sqrt{1-18\beta ^2{{\mathcal {K}}}^2}\right] ,\nonumber \\ {r_-}_{{}_{{}_{{}_{{}_{\tiny Eq. (11)}}}}}= & {} \frac{1}{3\beta }\left[ \sqrt{1-18\beta ^2{{\mathcal {K}}}^2}-1\right] ,\nonumber \\ {r_+}_{{}_{{}_{{}_{{}_{\tiny Eq. (15)}}}}}= & {} Root(4y^4\beta \Lambda +2y-3\beta y^2-6\beta {{\mathcal {K}}}^2 ), \end{aligned}$$

(35)

where $Root(4y^4\beta \Lambda -3\beta y^2+2y+2)$ are the roots of the equation $(4y^4\beta \Lambda +2y-3\beta y^2-6\beta {{\mathcal {K}}}^2=0)$, which is proven to have one real root. The first equation of (35) shows that the dimensional parameter $\beta$ cannot be zero, which immediately means that the solution (11) has no correspondence in the GR limit. Moreover, Eq. (35) tells us that the parameter $\beta$ should be negative, so that the horizons have a positive real value when there is no charge. Moreover, Eq. (35) puts constraints on the parameter $\beta$, namely $\beta <\frac{1}{3{{\mathcal {K}}}\sqrt{2}}$. The behavior of the radial coordinate r via the parameter $\beta$ is represented in Fig. 1a. Also, we plot there the behavior of the radial coordinate r and the parameter $\beta$ for the third equation of (35).⁵ Thus, we continue our study of the thermodynamics assuming $\beta <0$, according to the previous analysis, and taking into account the outer event horizon $r_+$ only, which is consistent with $\beta <0$.

Fig. 3

Schematic plot of the radial coordinate r versus the dimensional parameter $\beta$ that characterizes the spherically symmetric black holes (11) and (15)

Using Eq. (33), the entropy of the black holes (11) and (15) are computed as

$$\begin{aligned} {S_+}_{{}_{{}_{{}_{{}_{\tiny Eq. (11)}}}}}= & {} \frac{\pi }{27\beta ^2}\left[ 1- \sqrt{1-18\beta ^2 {{\mathcal {K}}}^2}\right] ^2\left[ 2+\sqrt{1-18\beta ^2{{\mathcal {K}}}^2}\right] ,\nonumber \\ {S_+}_{{}_{{}_{{}_{{}_{\tiny Eq. (15)}}}}}= & {} \frac{\pi r_+{}^2}{4}\left[ 1+\beta r_+\right] . \end{aligned}$$

(36)

The first of Eq. (36) shows that we always have a positive entropy. The second of Eq. (36) tells us that $\beta <-\frac{1}{r_+}$, in order to get a positive entropy. Equation (36) are plotted in Fig. 2. Note that the entropy S is not proportional to the area of the horizon, due to Eq. (33). We also note that the entropy S is indeed proportional to the area (as it should) provided there is no Ricci scalar squared term, i.e., $f_{{\mathcal {R}}}=1$ (Figs. 3, 4).

Fig. 4

Schematic plot of the entropy of the two black holes (11) and (15) versus the dimensional parameter $\beta$

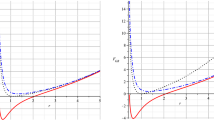
The Hawking temperatures associated with the black hole solutions (11) and (15) are, respectively,

$$\begin{aligned} {T_+}_{{}_{{}_{{}_{{}_{\tiny Eq. (11)}}}}}= & {} -\frac{3\beta \left[ 1-18\beta ^2 {{\mathcal {K}}}^2-\sqrt{1-18\beta ^2 {{\mathcal {K}}}^2}\right] ^2}{4\pi (1-\sqrt{1-18\beta ^2 {{\mathcal {K}}}^2})^3},\nonumber \\ {T_+}_{{}_{{}_{{}_{{}_{\tiny Eq. (15)}}}}}= & {} -\frac{2\beta [ 2\Lambda r_+{}^4+3{{\mathcal {K}}}^2]+r_+}{12\pi \beta r_+{}^3}, \end{aligned}$$

(37)

where ${T_+}$ is the Hawking temperature at the event horizon. We represent the Hawking temperature in Fig. 5. Figure 5a, which is related to the black hole (11), shows that we do have a positive temperature. As for Fig, 5b, which is related to the black hole (15), the temperature is always positive.

Fig. 5

Schematic plot of the temperature of the black holes (11) and (15) versus the dimensional parameter $\beta$

Using Eq. (34), the quasi-local energy of the two black holes (11) and (15) is calculated as

$$\begin{aligned} {E_+}_{{}_{{}_{{}_{{}_{\tiny Eq. (11)}}}}}= & {} -\frac{1+9\beta ^2 {{\mathcal {K}}}^2-\sqrt{1-18\beta ^2 {{\mathcal {K}}}^2}}{12 \beta },\nonumber \\ {E_+}_{{}_{{}_{{}_{{}_{\tiny Eq. (15)}}}}}= & {} \frac{r_+}{8}\left( 4+3\beta r_+\right) . \end{aligned}$$

(38)

Fig. 6

Schematic plot of the quasilocal energy of the two black holes (11) and (15) versus the dimensional parameter $\alpha$

Fig. 7

Schematic plot of the free energy of the black holes (11) and (15) versus the dimensional parameter $\beta$

The first equation of (38) shows that the dimensional parameter $\beta \ne 0$ and the quasi-local energy is always positive as Fig. 6 shows.

The free energy in the grand canonical ensemble, namely the Gibbs free energy, is defined as [83, 84]

$$\begin{aligned} G(r_+)=E(r_+)-T(r_+)S(r_+) \end{aligned}$$

(39)

where where $E(r_+)$, $T(r_+)$ and $S(r_+)$ are the quasilocal energy, the temperature and the entropy at the event horizon, respectively. Using Eqs. (36), (37) and (38) in (39), we get

$$\begin{aligned} {G_+}_{{}_{{}_{{}_{{}_{\tiny Eq. (11)}}}}}= & {} \frac{(5+9\beta ^2{{\mathcal {K}}}^2)\sqrt{1-18\beta ^2{{\mathcal {K}}}^2}-5+9\beta ^2{{\mathcal {K}}}^2}{36\beta (1-\sqrt{1-18\beta ^2{{\mathcal {K}}}^2})}, \nonumber \\ {G_+}_{{}_{{}_{{}_{{}_{\tiny Eq. (15)}}}}}= & {} \frac{r_+(4+3\beta r_+)}{8}\nonumber \\&+\frac{(r_++2\beta [2\Lambda \beta r_+{}^4+3\beta {{\mathcal {K}}}^2])(1+\beta r_+)}{12\beta r_+}.\nonumber \\ \end{aligned}$$

(40)

The behavior of the Gibbs energy of our black holes is depicted in Fig. 7a, b, for particular values of the parameters of the model.

7.1 Black hole thermodynamics in Einstein’s frame

In this section we will to repeat the previous calculations but this time in Einstein’s frame, i.e. using Eq. (31) to derive the thermodynamics of the black holes and compare them with the corresponding ones in (11) and (15).

The constraint $w(r(\bar{r_+})) = 0$ for the flat and AdS/Ad cases gives

$$\begin{aligned}&{{\bar{r}}}_+{}_{{}_{{}_{{}_{{}_{\tiny Eq. (11)}}}}}\nonumber \\&\quad =-\frac{\sqrt{6}}{18\beta (2\sqrt{36\beta ^2{{\mathcal {K}}}^2+324\beta ^4{{\mathcal {K}}}^4-3}-2-36\beta ^2{{\mathcal {K}}}^2)^{3/4}}\nonumber \\&\qquad \times \Big [\sqrt{2\sqrt{36\beta ^2{{\mathcal {K}}}^2{+}324\beta ^4{{\mathcal {K}}}^4-3}{-}2{-}36\beta ^2{{\mathcal {K}}}^2}\Big (1{+}18\beta ^2{{\mathcal {K}}}^2\nonumber \\&\qquad +\sqrt{36\beta ^2{{\mathcal {K}}}^2+324\beta ^4{{\mathcal {K}}}^4-3}\Big )-4\Big ],\nonumber \\ \end{aligned}$$

(41)

and for the AdS/dS case one gets an algebraic equation of 8th. order. Equation (41) shows that the dimensional parameter $\beta$ cannot be zero, as was already the case in the Jordan frame. Moreover, Eq. (41) tells us that the parameter $\beta$ must be negative, so that the horizons can have a positive real value when there is no charge. Also Eq. (41) shows that $\beta <\frac{1}{3{{\mathcal {K}}}\sqrt{2}}$ which is consistent with the restriction put on the dimensional parameter $\beta$ given in the Jordan frame after Eq. (35). The behavior of the radial coordinate r vs the parameter $\beta$ is depicted in Fig. 8a. Also, we plot the behavior of the radial coordinate r vs the parameter $\beta$ for the AdS/dS case.

Fig. 8

Schematic plot of the radial coordinate r versus the dimensional parameter $\beta$ that characterizes the spherically symmetric black holes (31)

Fig. 9

Schematic plot of the black hole temperature in Einstein’s frame versus the dimensional parameter $\beta$

The Hawking temperature for each of these black holes (31) is given by a lengthy expression, but their behaviors can be easily plotted, see Fig. 9. As is clear from Fig. 9, one gets a negative temperature for both black holes in Einstein’s frame. If we compare the results of the temperatures in the Jordan and Einstein frames we conclude that the physics of the two frames are not equivalent. This investigation shows in a clear way that in spite of the equivalence of the two frames from a mathematical viewpoint, and their sharing of many physical properties, the black hole thermodynamics are not equivalent. The entropy of the black hole (31) in the Einstein frame is defined as

$$\begin{aligned} {S_+}= \pi \bar{r}_+{}^2. \end{aligned}$$

(42)

Using Eq. (42) we compute the entropy of the solutions (31) as

$$\begin{aligned} {S_+}= & {} \frac{\pi }{54\beta ^2(2\sqrt{36\beta ^2{{\mathcal {K}}}^2 +324\beta ^4{{\mathcal {K}}}^4-3}-2-36\beta ^2{{\mathcal {K}}}^2)^{3/2}}\nonumber \\&\times \Big [-4+\sqrt{2\sqrt{36\beta ^2{{\mathcal {K}}}^2+324\beta ^4{{\mathcal {K}}}^4-3} -2-36\beta ^2{{\mathcal {K}}}^2}\nonumber \\&\Big (1+18\beta ^2{{\mathcal {K}}}^2+\sqrt{36\beta ^2{{\mathcal {K}}}^2+324\beta ^4{{\mathcal {K}}}^4-3}\Big )\Big ]^2, \nonumber \\&\times {S_+}_{{}_{{}_{{}_{{}_{AdS/dS}}}}}=\pi \bar{r}_+{}^2. \end{aligned}$$

(43)

Equation (43) are plotted in Fig. 10, showing that we have a positive entropy. We note that the entropy S is proportional to the area of the horizon, due to the fact that we are in Einstein’s frame.

Fig. 10

Schematic plot of the entropy of the two black holes in the Einstein frame versus the dimensional parameter $\alpha$

Using Eq. (34), the quasi-local energies of the two black holes (31) are calculated as

$$\begin{aligned} {E_+}_{{}_{{}_{{}_{{}_{\tiny Eq. (11)}}}}}= & {} -\frac{1+9\beta ^2 {{\mathcal {K}}}^2-\sqrt{1-18\beta ^2 {{\mathcal {K}}}^2}}{12 \beta },\nonumber \\ {E_+}_{{}_{{}_{{}_{{}_{\tiny Eq. (15)}}}}}= & {} \frac{\bar{r}_+}{8}\left( 4+3\beta \bar{r}_+\right) . \end{aligned}$$

(44)

The behavior of the quasi local energy is plotted in Fig. 11, which shows that we obtain a positive quasi local energy. The first equation of (44) shows that the dimensional parameter $\beta \ne 0$.

Fig. 11

Schematic plot of the quasilocal energies of the two black holes (11) and (15) versus the dimensional parameter $\alpha$ and $r_+$, respectively

Fig. 12

Schematic plot of the free energy and the free energy of the black hole (11)) versus the dimensional parameter $\alpha$ and $r_+$, respectively

The free energy is given by

$$\begin{aligned} G(r_+)=E({{\bar{r}}}_+)-T({{\bar{r}}}_+)S(r{{\bar{r}}}_+) \end{aligned}$$

(45)

where $E({{\bar{r}}}_+)$, $T({{\bar{r}}}_+)$ and $S({{\bar{r}}}_+)$ are the quasilocal energy, the temperature and the entropy at the event horizon, respectively. Using Eqs. (43) and (44) in (45), we get

$$\begin{aligned} {G_+}_{{}_{{}_{{}_{{}_{\tiny Eq. (11)}}}}}= & {} \frac{(5+9\beta ^2{{\mathcal {K}}}^2)\sqrt{1-18\beta ^2{{\mathcal {K}}}^2}-5+9\beta ^2{{\mathcal {K}}}^2}{36\beta (1-\sqrt{1-18\beta ^2{{\mathcal {K}}}^2})}, \nonumber \\ {G_+}_{{}_{{}_{{}_{{}_{\tiny Eq. (15)}}}}}= & {} \frac{{{\bar{r}}}_+(4+3\beta {{\bar{r}}}_+)}{8}\nonumber \\&+\frac{({{\bar{r}}}_++2\beta [2\Lambda \alpha {{\bar{r}}}_+{}^4+3\beta {{\mathcal {K}}}^2])(1+\beta {{\bar{r}}}_+)}{12\beta {{\bar{r}}}_+}.\nonumber \\ \end{aligned}$$

(46)

The behavior of the functions in (46) is depicted in Fig. 12a, b for particular values of the parameters of the model.

8 Stability of the black hole solutions in the Jordan and Einstein frames

To study the stability of the black hole solutions derived in the Jordan and Einstein frames, we will rewrite $f({{\mathcal {R}}})$ gravity in terms of the corresponding scalar-tensor theory. Neglecting the cosmological constant, the Lagrangian (2) can be recast as

$$\begin{aligned} {{\mathcal {S}}}=\frac{1}{2\kappa }\int d^{4}x\sqrt{-g}\,[\psi \, {{\mathcal {R}}}-V(\psi )], \end{aligned}$$

(47)

with $\psi$ being a scalar field coupled to the Ricci scalar ${{\mathcal {R}}}$ and $V(\psi )$ the potential of the system (see [60] for details). For our discussion of the stability of the solutions, we shall look at the behavior of the perturbations about a static spherically symmetric vacuum background, endowed with a metric of the form

$$\begin{aligned} {\mathrm {ds}^2}= & {} g_{\mu \nu }^{BG}dx^{\mu }dx^{\nu }=-w(r)\, dt^{2}\nonumber \\&+\frac{dr^{2}}{w_1(r)}+r^{2} ( d\theta ^{2} +\sin ^2\theta \, d\phi ^{2}). \end{aligned}$$

(48)

where $g_{\mu \nu }^{BG}$ is the background metric. The stability of the black holes obtained in the Jordan and Einstein frames proceeds by using linear perturbations and discussing what is the value of the speed of propagation of the scalar gravitational modes. The background equations of motion read

$$\begin{aligned} V= & {} - {\frac{4w_1\, \psi '}{r}}-{\frac{2\psi \, w'w_1}{w r}} -\frac{\psi ' w'w_1}{w}+{\frac{2\psi }{{r}^{2}}} -{\frac{2w_1\, \psi }{{r}^{2}}}\, , \nonumber \\ \psi ''= & {} -\frac{w'_1\psi '}{2w_1}{-}\frac{\psi w'_1}{rw_1} {+}\frac{w'\psi '}{2w}{+}\frac{\psi w'}{rw}\,, \qquad {{\mathcal {R}}} {=}\frac{dV}{d\psi }\,. \end{aligned}$$

(49)

The $'$ stands for differentiation w.r.t r.

8.1 Brief review of the Regge–Wheeler–Zerilli prescription

We shal now give an outline of the prescription developed by Regge, Wheeler [85], and Zerilli [86] to decompose the metric perturbations according to their transformation properties under two-dimensional rotations. Although these authors studied the perturbations of the Schwarzschild black hole in GR, the prescription mainly depends on the properties of spherical symmetry and, therefore, it can be used in modified $f({{\mathcal {R}}})$ gravity, as well.

We start from the slightly perturbed metric corresponding to a static spherically symmetric space-time, $g_{\mu \nu }=g_{\mu \nu }^{BG}+h_{\mu \nu }$, where $h_{\mu \nu }$ stands for an infinitesimal quantity. In the linear approximation, the perturbations are assumed to be small w.r.t the background, i.e., $g_{\mu \nu }^{0}>> h_{\mu \nu }$. Therefore, under two-dimensional rotations on a sphere, the components $h_{tt},h_{tr}$ and $h_{rr}$ transform as scalars, while the components $h_{ta}$ and $h_{ra}$ transform as vectors, and $h_{ab}$ transforms as a tensor (here a, b are either $\theta$ or $\phi$). Any scalar quantity $\Psi$ can be written in terms of spherical harmonics $Y_{\ell m}(\theta ,\phi )$, thus

$$\begin{aligned} \Psi (t,r,\theta ,\phi )=\sum _{\ell ,m}\Phi _{\ell m}(t,r)Y_{\ell m}(\theta ,\varphi ). \end{aligned}$$

(50)

In a spherically symmetric space-time the solution will be independent of the index m, so that this index can be neglected and we can just consider the index $\ell$, which describes the multipole number and appears due to the separation of the angular variables through the expansion into spherical harmonics

$$\begin{aligned} \Delta _{\theta , \phi }Y_{\ell }(\theta , \phi )=-\ell (\ell +1)Y_{\ell }(\theta , \phi ). \end{aligned}$$

(51)

By the way, this is similar to what happens for the hydrogen atom problem in quantum mechanics when dealing with the Schrödinger equation. Any vector $V_{a}$ can be decomposed into a divergent part and a divergence-free part, as

$$\begin{aligned} V_{a}(t,r,\theta ,\phi )=\nabla _{a}\Psi _{1}+E_{a}^b\nabla _b\Psi _{2}, \end{aligned}$$

(52)

with $\Psi _{1}$ and $\Psi _{2}$ being two scalars and $E_{ab}\equiv \sqrt{\det \gamma }~\epsilon _{ab}$, where $\gamma _{ab}$ is the two-dimensional metric on the sphere and $\epsilon _{ab}$ is the usual totally anti-symmetric symbol, with $\epsilon _{\theta \varphi }=1$. Here, $\nabla _{a}$ stands for the covariant derivative w.r.t. the metric $\gamma _{ab}$. Given that $V_{a}$ is a two-component vector, it is completely specified by the quantities $\Psi _{1}$ and $\Psi _{2}$. Therefore, one can apply the scalar decomposition (50) to $\Psi _{1}$ and $\Psi _{2}$ in order to express the vector quantity $V_a$ in spherical harmonics.

Finally, any symmetric tensor $T_{ab}$ can be decomposed as

$$\begin{aligned} T_{ab}(t,r,\theta ,\phi )= & {} \nabla _{a}\nabla _{b}\Psi _{1} +\gamma _{ab}\Psi _{2}\nonumber \\&+\frac{1}{2}\left( E_{a}{}^{c}\nabla _{c}\nabla _{b}\Psi _{3}+ E_{b}{}^{c}\nabla _{c}\nabla _{a}\Psi _{3}\right) , \end{aligned}$$

(53)

where $\Psi _{1},~\Psi _{2}$ and $\Psi _{3}$ are three scalar quantities. Since $A_{ab}$ has three independent components, $\Psi _{1},~\Psi _{2}$ and $\Psi _{3}$ completely specify $A_{ab}$. Therefore, one can use the scalar decomposition (50) with $\Psi _{1},~\Psi _{2}$ and $\Psi _{3}$, in order to decompose the tensor quantity $A_{ab}$ into spherical harmonics. We refer to the variables corresponding to $E_{ab}$ as odd-type variables and to the rest as even-type ones. What does make this decomposition useful is the fact that, in the linearized equations of motion for $h_{\mu \nu }$, odd-type and even-type perturbations are fully decoupled. This fact sheds light on the invariance of the background space-time under parity transformations. In the following subsection we are going to study the odd-type perturbations.

8.2 Perturbations in $f({{\mathcal {R}}})$ gravity

$$\begin{aligned} \hbox {The odd modes} \end{aligned}$$

There are two kinds of vector spherical harmonics (polar and axial), which are build out of combinations of the Levi-Civita volume form and of the gradient operator acting on the scalar spherical harmonics. The essential difference between the two types is their parity. Under the parity operator $\pi$, a spherical harmonic with index $\ell$ transforms as $(-1)^\ell$, the polar class of perturbations transforming in the same way, as $(-1)^\ell$, and the axial perturbations as $(-1)^{\ell +1}$.

Using the Regge-Wheeler formalism, the odd-type metric perturbations can be written as

$$\begin{aligned} h_{tt}= & {} 0,~~~h_{tr}=0,~~~h_{rr}=0, \end{aligned}$$

(54)

$$\begin{aligned} h_{ta}= & {} \sum _{\ell , m}h_{0,\ell m}(t,r)E_{ab}\partial ^{b}Y_{\ell m}(\theta ,\varphi ), \end{aligned}$$

(55)

$$\begin{aligned} h_{ra}= & {} \sum _{\ell , m}h_{1,\ell m}(t,r)E_{ab}\partial ^{b}Y_{\ell m}(\theta ,\varphi ), \end{aligned}$$

(56)

$$\begin{aligned} h_{ab}= & {} \frac{1}{2}\sum _{\ell , m}h_{2,\ell m}(t,r)\left[ E_{a}^{~c}\nabla _{c}\nabla _{b}Y_{\ell m}(\theta ,\varphi )\right. \nonumber \\&\left. +E_{b}^{~c}\nabla _{c}\nabla _{a}Y_{\ell m}(\theta ,\varphi )\right] . \end{aligned}$$

(57)

Using the gauge transformation $x^{\mu }\rightarrow x^{\mu }+\xi ^{\mu }$, where the components $\xi ^{\mu }$ are infinitesimal, we can show that not all the metric perturbations are physical, and that some of them can be actually set to vanish. For the odd-type perturbations, we can consider the following gauge transformation

$$\begin{aligned} \xi _{t}=\xi _{r}=0,\,\, \xi _{a}=\sum _{\ell m}\Lambda _{\ell m}(t,r)E_{a}^{~b}\nabla _{b}Y_{\ell m}, \end{aligned}$$

(58)

where $\Lambda _{\ell m}$ can always be set to vanish, as $h_{2,\ell m}$ (Regge-Wheeler gauge). By this procedure, $\Lambda _{\ell m}$ is completely fixed and there are no remaining gauge degrees of freedom. Then, after substituting the metric into the action (47) and performing integration by parts, we find that the action for the odd modes becomes

$$\begin{aligned} S_{{ odd}}= & {} \frac{1}{2\kappa } \sum _{\ell ,m}\int dt\, dr\,{{\mathcal {L}}}_{{ odd}}\nonumber \\= & {} \frac{1}{4\kappa } \sum _{\ell ,m}\int dt\, dr\,j^{2}\Bigg [\frac{\phi \sqrt{w_1}}{\sqrt{w}}\Big \{{\left( {\dot{h}_{1}}-h_{0}'\right) }^{2} +\frac{8h_{0}{\dot{h}_{1}}}{r}\Big \}\nonumber \\&+ \frac{h_{0}^{2}}{r^{2}}\left\{ 4r\Bigg [\frac{\phi \sqrt{w_1}}{\sqrt{w}}\Bigg ]'+4\frac{\phi \sqrt{w_1}}{\sqrt{w}} +\frac{(j^2-2)\phi }{\sqrt{ww_1}} \right\} \nonumber \\&-\frac{\,(j^{2}-2)\,\sqrt{ww_1}\, \phi \, h_{1}^{2}}{r^{2}}\Bigg ], \end{aligned}$$

(59)

where we have dropped the suffix $\ell$ for the fields, and $j^{2}=\ell \,(\ell +1)$. Variation of (59) w.r.t. $h_{0}$ yields

$$\begin{aligned} \Bigg [\phi \sqrt{\frac{w_1}{w}}(h_{0}'-\dot{h}_{1})\Bigg ]'= \frac{ h_{0}}{r^{2}}\left\{ 4r\Bigg [\frac{\phi \sqrt{w_1}}{\sqrt{w}}\Bigg ]'+4\frac{\phi \sqrt{w_1}}{\sqrt{w}}\right. \nonumber \\ \quad \left. +\frac{(j^2-2)\phi }{\sqrt{ww_1}} \right\} +\frac{4\phi \sqrt{\frac{w_1}{w}}\,\dot{h}_{1}}{r}\,, \end{aligned}$$

(60)

that cannot be solved for $h_{0}$. Therefore, we are going to rewrite the action (59) as

$$\begin{aligned} {L}_{{ odd}}= & {} \frac{j^{2}\, \phi \sqrt{w_1}}{2\sqrt{w}}{\left( {\dot{h}_{1}}-h_{0}'+\frac{2\,{h_0}}{r}\right) }^{2}\nonumber \\&-\frac{j^{2}\Bigg (\frac{\phi \sqrt{w_1}}{\sqrt{w}}+r\Bigg \{\frac{\phi \sqrt{w_1}}{\sqrt{w}}\Bigg \}'\Bigg )\,h_{0}{}^2}{r^2}\nonumber \\&+\frac{j^{2}\,h_{0}^{2}}{r^{2}}\left\{ 4r\Bigg [\frac{\phi \sqrt{w_1}}{\sqrt{w}}\Bigg ]'+4\frac{\phi \sqrt{w_1}}{\sqrt{w}} +\frac{(j^2-2)\phi }{\sqrt{ww_1}} \right\} \nonumber \\&-\frac{j^2\,(j^{2}-2)\,\sqrt{ww_1}\, \phi \, h_{1}^{2}}{r^{2}}, \end{aligned}$$

(61)

so that all the terms containing $\dot{h}_{1}$ are inside the first squared term. Using a Lagrange multiplier, Q, Eq. (61) can be rewritten as follows

$$\begin{aligned} {L}_{{ odd}}= & {} \frac{j^{2}\, \psi \sqrt{w_1}}{2\sqrt{w}}\left[ 2\, Q\left( \dot{h}_{{1}}-h'_{{0}}+{\frac{2\,h_{{0}}}{r}}\right) -Q^{2}\right] \nonumber \\&-\frac{j^{2}\Bigg (\frac{\psi \sqrt{w_1}}{\sqrt{w}}+r\Bigg \{\frac{\psi \sqrt{w_1}}{\sqrt{w}}\Bigg \}'\Bigg )\,h_{0}{}^2}{r^2}\nonumber \\&+\frac{j^{2}\,h_{0}^{2}}{r^{2}}\left\{ 4r\Bigg [\frac{\psi \sqrt{w_1}}{\sqrt{w}}\Bigg ]'{+}4\frac{\psi \sqrt{w_1}}{\sqrt{w}} {+}\frac{j^2(j^2-2)\phi }{\sqrt{ww_1}} \right\} \nonumber \\&-\frac{j^2\,(j^{2}-2)\,\sqrt{ww_1}\, \phi \, h_{1}^{2}}{r^{2}}. \end{aligned}$$

(62)

Eq. (62) shows that both fields, $h_{0}$ and $h_{1}$, can be integrated out by using their own equations of motion, which can be written as

$$\begin{aligned} h_{1}= & {} -\frac{r^2\,\dot{Q}}{(j^{2}-2)w}\,, \end{aligned}$$

(63)

$$\begin{aligned} h_{0}= & {} \frac{r\Bigg [\Bigg (\frac{2\phi \sqrt{w_1}}{\sqrt{w}}+r\Bigg \{\frac{\psi \sqrt{w_1}}{\sqrt{w}}\Bigg \}'\Bigg )\, Q+\frac{r\, \psi \sqrt{w_1}}{2\sqrt{w}} Q'\Bigg ]}{2\Bigg (\frac{\psi \sqrt{w_1}}{\sqrt{w}}+r\Bigg \{\frac{\psi \sqrt{w_1}}{\sqrt{w}}\Bigg \}'\Bigg )-\Bigg (\frac{\psi \sqrt{w_1}}{\sqrt{w}}+r\Bigg \{\frac{\psi \sqrt{w_1}}{\sqrt{w}}\Bigg \}'\Bigg )}\,.\nonumber \\ \end{aligned}$$

(64)

These relations link the physical modes $h_{0}$ and $h_{1}$ to the auxiliary field Q. Once Q is known, also $h_{0}$ and $h_{1}$ are. After substituting these expressions into the Lagrangian and performing an integration by parts for the term proportional to $Q'\, Q$, one gets the Lagrangian in the canonical form

$$\begin{aligned} {L}_{{odd}}=\frac{s_1{}^2}{s_2}\,\dot{Q}^{2}- \frac{s_1{}^2\,r^{2}}{s_3r^2-2rs'_1-2s_1}\,Q'^{2}-\nu _1{}^{2}\, Q^{2}\,, \end{aligned}$$

(65)

where

$$\begin{aligned}&s_1=\frac{j^2\psi \sqrt{w_1}}{2\sqrt{w}},\quad s_2=\frac{j^2\psi (j^2-2)\sqrt{ww_1}}{2r^2}, \nonumber \\&s_3=\frac{j^2}{r^2}\Bigg (\frac{\psi \sqrt{w_1}}{\sqrt{w}}+r\Bigg \{\frac{\psi \sqrt{w_1}}{\sqrt{w}}\Bigg \}'+\frac{(j^2-2)\psi }{2\sqrt{ww_1}}\Bigg ),\nonumber \\&\nu _1{}^{2}=\frac{s_1r^2\Big [r^2s'_1s'_3-r^2s''_1s_3+2s_1s_3+4s'_1{}^2+r^2s_3{}^2-2s_1s''_1+2rs_1s'_3-4rs'_1s_3\Big ]}{(2s_1+2rs'_1-r^2s_3)^2}\,. \end{aligned}$$

(66)

From Eq. (65), we can derive the no ghost conditions

$$\begin{aligned} s_2\ge 2\,,\qquad { \hbox {that leads to }\,\qquad }j^2\ge 2\,. \end{aligned}$$

For solutions proportional to $e^{i(\omega t-kr)}$ with large k and $\omega$, we have the radial dispersion relation

$$\begin{aligned} \omega ^{2}=ww_1\, k^{2}, \end{aligned}$$

where we have made use of the background equations of motion. Finally the expression for the radial speed reads

$$\begin{aligned} c_{{ odd}}^{2}=\left( \frac{dr_{*}}{d\tau }\right) ^2=1\,, \end{aligned}$$

where the radial tortoise coordinate ($dr_{*}^{2}=dr^{2}/w_1$) and the proper time ($d\tau ^{2}=w_1\, dt^{2}$) have been employed.

9 Black hole stability analysis using geodesic deviations in Jordan’s frame

Test particle trajectories in a gravitational field are obtained from the geodesic equations

$$\begin{aligned} {d^2 x^\sigma \over d\tau ^2}+ \left\{ ^\sigma _{ \mu \nu } \right\} {d x^\mu \over d\tau }{d x^\nu \over d\tau }=0, \end{aligned}$$

(67)

with $\tau$ being the affine connection parameter along the geodesic. The geodesic deviation takes the form [87, 88]

$$\begin{aligned} {d^2 \xi ^\sigma \over d\tau ^2}+ 2\left\{ ^\sigma _{ \mu \nu } \right\} {d x^\mu \over d\tau }{d \xi ^\nu \over d\tau }+ \left\{ ^\sigma _{ \mu \nu } \right\} _{,\ \rho } {d x^\mu \over d\tau }{d x^\nu \over d\tau }\xi ^\rho =0, \end{aligned}$$

(68)

where $\xi ^\rho$ is the deviation 4-vector. Introducing (67) and (68) into (9), we get for the geodesic equations

$$\begin{aligned} {d^2 t \over d\tau ^2}= & {} 0, \qquad {1 \over 2} w'(r)\left( {d t \over d\tau }\right) ^2-r\left( {d \phi \over d\tau }\right) ^2=0, \nonumber \\ {d^{2} \theta \over d\tau ^2}= & {} 0,\qquad {d^2 \phi \over d\tau ^2}=0, \end{aligned}$$

(69)

and for the geodesic deviation

$$\begin{aligned}&{d^2 \xi ^1 \over d\tau ^2}+w(r)w'(r) {dt \over d\tau }{d \xi ^0 \over d\tau }-2r w(r) {d \phi \over d\tau }{d \xi ^3 \over d\tau }\nonumber \\&\quad +\left[ {1\over 2}\left( w'^2(r)+w(r) w''(r) \right) \left( {dt \over d\tau }\right) ^2\right. \nonumber \\&\quad \left. -\left( w(r)+rw'(r) \right) \left( {d\phi \over d\tau }\right) ^2 \right] \xi ^1=0, \nonumber \\&{d^2 \xi ^0 \over d\tau ^2}+{w'(r) \over w(r)}{dt \over d\tau }{d \zeta ^1 \over d\tau }=0,\quad {d^2 \xi ^2 \over d\tau ^2}+\left( {d\phi \over d\tau }\right) ^2 \xi ^2=0, \nonumber \\&{d^2 \xi ^3 \over d\tau ^2}+{2 \over r}{d\phi \over d\tau } {d \xi ^1 \over d\tau }=0, \end{aligned}$$

(70)

where w(r) is defined by the metric (18) or (19), $w'(r)=\displaystyle {dw(r) \over dr}$. Using the circular orbit

$$\begin{aligned} \theta ={\pi \over 2}, \qquad {d\theta \over d\tau }=0, \qquad {d r \over d\tau }=0, \end{aligned}$$

(71)

we get

$$\begin{aligned} \left( {d\phi \over d\tau }\right) ^2= & {} {w'(r) \over r[2w(r)-rw'(r)]},\nonumber \\ \left( {dt \over d\tau }\right) ^2= & {} {2 \over 2w(r)-rw'(r)}. \end{aligned}$$

(72)

Fig. 13

Schematic plot of Eq. (76), namely $\sigma ^2$ versus the coordinate r

Equation (70) can be rewritten as

$$\begin{aligned}&{d^2 \xi ^1 \over d\phi ^2}+w(r)w'(r) {dt \over d\phi }{d \xi ^0 \over d\phi }-2r w(r) {d \xi ^3 \over d\phi }\nonumber \\&\quad +\left[ {1 \over 2}\left[ w'^2(r)+w(r) w''(r) \right] \left( {dt \over d\phi }\right) ^2\right. \nonumber \\&\quad \left. -\left[ w(r)+rw'(r) \right] \right] \zeta ^1=0, \nonumber \\&\quad {d^2 \xi ^2 \over d\phi ^2}+\xi ^2=0, \qquad {d^2 \xi ^0 \over d\phi ^2} +{w'(r) \over w(r)}{dt \over d\phi }{d \xi ^1 \over d\phi }=0,\nonumber \\&\quad {d^2 \xi ^3 \over d\phi ^2}+{2 \over r} {d \xi ^1 \over d\phi }=0. \end{aligned}$$

(73)

The second equation of (73) corresponds to a simple harmonic motion, what means that the motion on the plane $\theta =\pi /2$ is stable. Assuming the solutions of the remaining equations of (73) have the form

$$\begin{aligned} \xi ^0= & {} \zeta _1 e^{i \sigma \phi }, \qquad \xi ^1= \zeta _2e^{i \sigma \phi }, \qquad and \nonumber \\ \xi ^3= & {} \zeta _3 e^{i \sigma \phi }, \end{aligned}$$

(74)

where $\zeta _1, \zeta _2$ and $\zeta _3$ are constant and the variable $\phi$ has to be determined. Substituting (74) into (73), we get

$$\begin{aligned} \displaystyle \frac{3ww'-\sigma ^2w'-2rw'^2+rww''}{w'}>0, \end{aligned}$$

(75)

which is the stability condition for any charged static spherically symmetric space-time. The condition (75) for the black holes (18) and (19) can be rewritten as

$$\begin{aligned} \sigma ^2= & {} \frac{2r^2+\beta r^3+18{{\mathcal {K}}}^2\beta r+48\beta ^2{{\mathcal {K}}}^4+4r^4\beta \Lambda [5r+4r^2 \beta +24\beta {{\mathcal {K}}}^2]}{2\beta r^2(r+6\beta {{\mathcal {K}}}^2+4r^4\beta \Lambda )}>0. \end{aligned}$$

(76)

Figure 13 is a plot of Eq. (76) for particular values of the models. It exhibits the regions where the black holes are stable and the regions where there is no possible stability.

Fig. 14

Schematic plot of Eq. (81), namely $\sigma ^2$ versus the coordinate r

9.1 Black hole stability analysis using geodesic deviation in Einstein’s frame

Introducing (67) and (68) into (31), we get for the geodesic equations

$$\begin{aligned} {d^2 t \over d\tau ^2}= & {} 0, \qquad {1 \over 2} w'_1(\bar{r})\left( {d t \over d\tau }\right) ^2-\bar{r}\left( {d \phi \over d\tau }\right) ^2=0,\nonumber \\ {d^2 \theta \over d\tau ^2}= & {} 0,\qquad {d^2 \phi \over d\tau ^2}=0, \end{aligned}$$

(77)

and for the geodesic deviation

$$\begin{aligned}&{d^2 \xi ^1 \over d\tau ^2}+w(\bar{r})w'_1(\bar{r}) {dt \over d\tau }{d \xi ^0 \over d\tau }-2\bar{r} w(\bar{r}) {d \phi \over d\tau }{d \xi ^3 \over d\tau }\nonumber \\&\quad +\left[ {1 \over 2}\left[ w'(\bar{r})w'_1(\bar{r})+w(\bar{r}) w''_1(\bar{r}) \right] \left( {dt \over d\tau }\right) ^2\right. \nonumber \\&\quad \left. -\left[ w(\bar{r})+\bar{r}w'(\bar{r}) \right] \left( {d\phi \over d\tau }\right) ^2 \right] \xi ^1=0, \nonumber \\&\quad {d^2 \xi ^0 \over d\tau ^2}+{w'_1(\bar{r}) \over w_1(\bar{r})}{dt \over d\tau }{d \zeta ^1 \over d\tau }=0,\nonumber \\&\quad {d^2 \xi ^2 \over d\tau ^2}+\left( {d\phi \over d\tau }\right) ^2 \xi ^2=0,\qquad {d^2 \xi ^3 \over d\tau ^2}+{2 \over \bar{r}}{d\phi \over d\tau } {d \xi ^1 \over d\tau }=0,\nonumber \\ \end{aligned}$$

(78)

where $w(\bar{r})$ is defined by the metric (31) $w'(\bar{r})=\displaystyle {dw(\bar{r}) \over d\bar{r}}$ and $w'_1(\bar{r})=\displaystyle {dw_1(\bar{r}) \over d\bar{r}}$. Using the circular orbit

$$\begin{aligned} \theta ={\pi \over 2}, \qquad {d\theta \over d\tau }=0, \qquad {d \bar{r} \over d\tau }=0, \end{aligned}$$

(79)

we get

$$\begin{aligned} \left( {d\phi \over d\tau }\right) ^2={w'_1(\bar{r}) \over \bar{r}[2w(\bar{r})-\bar{r}w'(\bar{r})]}, \qquad \left( {dt \over d\tau }\right) ^2={2 \over 2w(\bar{r})-w'(\bar{r})}.\nonumber \\ \end{aligned}$$

(80)

Equation (78) can be rewritten as

$$\begin{aligned}&{d^2 \xi ^1 \over d\phi ^2}+w(\bar{r})w'_1(\bar{r}) {dt \over d\phi }{d \xi ^0 \over d\phi }-2\bar{r} w'(\bar{r}) {d \xi ^3 \over d\phi } \nonumber \\&\quad +\left[ {1 \over 2}\left[ w'(\bar{r})w'_1(\bar{r})+w(\bar{r}) w''_1(\bar{r}) \right] \left( {dt \over d\phi }\right) ^2\right. \nonumber \\&\quad \left. -\left[ w(\bar{r})+\bar{r}w'(\bar{r}) \right] \right] \zeta ^1=0, \nonumber \\&\quad {d^2 \xi ^2 \over d\phi ^2}+\xi ^2=0, \qquad {d^2 \xi ^0 \over d\phi ^2}\nonumber \\&\quad +{w'(\bar{r}) \over w(\bar{r})}{dt \over d\phi }{d \xi ^1 \over d\phi }=0,\qquad {d^2 \xi ^3 \over d\phi ^2}+{2 \over \bar{r}} {d \xi ^1 \over d\phi }=0. \end{aligned}$$

(81)

The second equation of (81) corresponds to simple harmonic motion, which means that the motion on the plane $\theta =\pi /2$ is stable. Now, the solutions of the remaining equations of (81) are

$$\begin{aligned} \xi ^0 = \zeta _1 e^{i \omega \phi }, \qquad \xi ^1= \zeta _2e^{i \omega \phi }, \qquad and \qquad \xi ^3 = \zeta _3 e^{i \omega \phi },\nonumber \\ \end{aligned}$$

(82)

where $\zeta _1, \zeta _2$ and $\zeta _3$ are constant and the variable $\phi$ has to be determined. Substituting (82) into (81) one gets a quite lengthy expression, which is depicted in Fig. 14. This plot shows that black holes in the Einstein frame have always some non-void stability region.

9.2 Causal structure of the solutions

We shall now discuss the causal structure of the space-time (13). For that purpose, we start from the metric

$$\begin{aligned} ds^2 = - \mathrm {e}^{2\nu (r)} dt^2 + \mathrm {e}^{-2\nu (r)} dr^2 + r^2 \sum _{i,j=1}^{2} {\tilde{g}}_{ij} dx^i dx^j\, , \end{aligned}$$

(83)

with

$$\begin{aligned} \mathrm {e}^{2\nu } = C^2 - \frac{M}{r} \, , \quad C>0 \, , \end{aligned}$$

(84)

the metric of the unit sphere being ${\tilde{g}}_{ij}$, and we consider the region where $r \gg M$. Then, the metric in (83) reduces to

$$\begin{aligned} ds_\mathrm {as}^2 = - C^2 dt^2 + \frac{dr^2}{C^2} + r^2 \sum _{i,j=1}^{2} {\tilde{g}}_{ij} dx^i dx^j\, . \end{aligned}$$

(85)

Redefining,

$$\begin{aligned} t=\frac{{\tilde{t}}}{C}\, , \quad r=C{\tilde{r}}\, , \end{aligned}$$

(86)

we find

$$\begin{aligned} ds_\mathrm {as}^2 = - d{{\tilde{t}}}^2 + d{{\tilde{r}}}^2 + C^2 {{\tilde{r}}}^2 \sum _{i,j=1}^{2} {\tilde{g}}_{ij} dx^i dx^j\, , \end{aligned}$$

(87)

which is not Lorentz invariant unless $C=1$. In order to clarify the situation, we choose ${\tilde{g}}_{ij}$ as

$$\begin{aligned} \sum _{i,j=1}^{2} {\tilde{g}}_{ij} dx^i dx^j = d\theta ^2 + \sin ^2 \theta d\phi ^2 \, , \end{aligned}$$

(88)

with $0\le \theta \le \pi$ and $0\le \phi < 2\pi$, and we consider the hypersurface with $\theta =\frac{\pi }{2}$. Then, the metric reads

$$\begin{aligned} ds_\mathrm {hyp}^2 = - d{{\tilde{t}}}^2 + d{{\tilde{r}}}^2 + C^2 d\phi ^2 \, . \end{aligned}$$

(89)

If we redefine,

$$\begin{aligned} \phi = C^{-1} {{\tilde{\phi }}}\, , \end{aligned}$$

(90)

the metric acquires the following form

$$\begin{aligned} ds_\mathrm {hyp}^2 = - d{{\tilde{t}}}^2 + d{{\tilde{r}}}^2 + d{{\tilde{\phi }}}^2 \, , \end{aligned}$$

(91)

which is nothing but the metric of flat three-dimensional space-time. We should note, however, that $0\le {\tilde{\phi }} \le 2C\pi$, and therefore if $C<1$, a deficit angle appears, while if $C>1$ a surplus angle shows up (see Fig. 15 for the case $C=\frac{3}{4}<1$ and Fig. 16 for the case $C=\frac{5}{4}>1$). For $C<1$ the light emitted from a point reaches another point in two orbits of the light trajectory (see Fig. 17) and, therefore, multiple light-cone surfaces are formed. On the contrary, in the other case the light ray emitted from a point ${\tilde{\phi }}=\pi$ and ${\tilde{r}}=r_0$ ($r_0$ is a constant) does not reach the region $2\pi< {\tilde{\phi }} < 2C\pi$ (see Fig. 18) and, therefore, the light-cone surface has a boundary. In such space-time, one cannot separate time-like regions from space-like ones and all kind of problems with causality may show up.

Fig. 15

Structure of the spatial part for $C=\frac{3}{4}<1$. We identify two arrows and glue the space there

Fig. 16

Structure of the spatial part for $C=\frac{5}{4}>1$. We identify two arrow and glue the space there

Fig. 17

The point $B'$ is identified with the point B. When $C=\frac{3}{4}<1$, the light emitted at point A may reach point $B=B'$ along two different paths

Fig. 18

When $C=\frac{5}{4}>1$, the light emitted at point A (${\tilde{\phi }}=\pi$ and ${\tilde{r}}=r_0$, $r_0$ is a constant) cannot reach the shaded region ($2\pi< {\tilde{\phi }} < \frac{5}{2}\pi = 2C\pi$

10 Alternative black hole description from a generalized fluid model

10.1 Relation between the space-time geometry and an equation of state

We will here consider the relation existing between the space-time geometry and an equation of state for General Relativity with a cosmological fluid. We start from the space-time metric (83), from where we have

$$\begin{aligned}&R_{tt}= \frac{1}{2} \left( C + \frac{r^2}{l^2} - \frac{M}{r} + \frac{q^2}{r^2} \right) \left( \frac{6}{l^2} + \frac{2q^2}{r^4} \right) \, , \nonumber \\&R_{rr}= - \frac{1}{2} \left( C + \frac{r^2}{l^2} - \frac{M}{r} + \frac{q^2}{r^2} \right) ^{-1} \left( \frac{6}{l^2} + \frac{2q^2}{r^4} \right) \, , \nonumber \\&R_{ij}= \left( 1 - C - \frac{3r^2}{l^2} + \frac{q^2}{r^2} \right) {\tilde{g}}_{ij}\, , \nonumber \\&R= - \frac{12}{l^2} - \frac{2\left( C - 1 \right) }{r^2} \, . \end{aligned}$$

(92)

Using now the Einstein equation

$$\begin{aligned} R_{\mu \nu } - \frac{1}{2}g_{\mu \nu } R = \kappa ^2 T_{\mu \nu } \, , \end{aligned}$$

(93)

we find

$$\begin{aligned} \kappa ^2 T_{tt} =&- \kappa ^2 T_{rr}\nonumber \\ =&\left( C + \frac{r^2}{l^2} - \frac{M}{r} + \frac{q^2}{r^2} \right) \left( - \frac{3}{l^2} - \frac{C - 1}{r^2} + \frac{q^2}{r^4} \right) \, , \nonumber \\ \kappa ^2 T_{ij} =&\left( \frac{3r^2}{l^2} + \frac{q^2}{r^2} \right) {\tilde{g}}_{ij} \end{aligned}$$

(94)

We now define the energy density $\rho$, the pressure in the radial direction $p_r$, and the pressure in the angular direction $p_a$, as

$$\begin{aligned} T_{tt}= - g_{tt} \rho \, , \quad T_{rr}= g_{rr} p_r \, , \quad T_{ij} = g_{ij} p_a \, , \end{aligned}$$

(95)

with the result

$$\begin{aligned} \kappa ^2 \rho= & {} - \left( - \frac{3}{l^2} - \frac{C - 1}{r^2} + \frac{q^2}{r^4} \right) \, , \nonumber \\ \kappa ^2 p_r= & {} - \left( -\frac{3}{l^2} - \frac{C - 1}{r^2} + \frac{q^2}{r^4} \right) \, ,\nonumber \\ \kappa ^2 p_a= & {} \frac{3}{l^2} + \frac{q^2}{r^4} \, , \end{aligned}$$

(96)

which yields the following equation of state (EoS) for the cosmic fluid

$$\begin{aligned} \rho = p_r = - p_a + \frac{6}{\kappa ^2 l^2} + \frac{C - 1}{\kappa ^2 q} \sqrt{ \kappa ^2 p_a - \frac{3}{l^2} }\, . \end{aligned}$$

(97)

In particular, when $\frac{1}{l}=0$, we find

$$\begin{aligned} \rho = p_r = - p_a + \frac{C - 1}{\kappa q} \sqrt{ p_a }\, . \end{aligned}$$

(98)

Equation (97) tells us that $p_a\ge \frac{3}{\kappa ^2 l^2}$, and so the quantity inside the square root is positive. In particular, in the case $\frac{1}{l}=0$, as in (98), we find $p_a\ge 0$. And, in order that $\rho \ge 0$, we get $p_a\le \frac{\left( C - 1\right) ^2 }{\kappa ^2 q^2}$. Then, it follows that

$$\begin{aligned} 0\le p_a \le \frac{\left( C - 1\right) ^2 }{\kappa ^2 q^2} \, . \end{aligned}$$

(99)

In the case $\frac{1}{l}\ne 0$, corresponding to Eq. (97), the restriction associated to (98) becomes somehow involved, as follows

$$\begin{aligned} \frac{3}{\kappa ^2 l^2}\le & {} p_a \le \frac{1}{2} \left( \frac{12}{\kappa ^2 l^2} + \frac{\left( C-1 \right) ^2}{\kappa ^2 q^2}\right. \nonumber \\&\left. + \sqrt{ \frac{12\left( C-1 \right) ^2}{\kappa ^4 l^2 q^2} + \frac{\left( C-1 \right) ^4}{\kappa ^4 q^4}} \right) \, . \end{aligned}$$

(100)

For $\frac{1}{l}=0$ in (98), the pressures $p_r$ and $p_a$ should be positive if we assume that the energy density $\rho$ is positive. We should note, however, that when $\frac{1}{l^2}<0$ in (97), $p_a$ can be negative, as indeed found from (101). Therefore, this fluid can act as dark energy, what is indeed clear from the assumption (83), where the metric behaves as the de Sitter space-time for large r, when $\frac{1}{l^2}<0$.

$$\begin{aligned}&p_a^2 - \frac{12}{\kappa ^2 l^2} + \frac{36}{\kappa ^2 l^2} p_a = \frac{\left( C-1 \right) ^2}{\kappa ^4 q^2} \left( \kappa ^2 p_a - \frac{3}{l^2} \right) \nonumber \\&\qquad \times \frac{3}{\kappa ^2 l^2} \le p_a \le \frac{1}{2} \left( \frac{12}{\kappa ^2 l^2} + \frac{\left( C-1 \right) ^2}{\kappa ^2 q^2} \right. \nonumber \\&\qquad \left. + \sqrt{ \left( \frac{12}{\kappa ^2 l^2} + \frac{\left( C-1 \right) ^2}{\kappa ^2 q^2} \right) ^2 - \frac{144}{\kappa ^4 l^4} - \frac{12\left( C-1 \right) ^2}{\kappa ^4 l^2 q^2}} \right) .\nonumber \\ \end{aligned}$$

(101)

In summary, we have here derived the same BH solution as in usual general relativity with a cosmological fluid, which may be intrepreted as kin ad of dark energy. This is a clear indication of the universality of the BH solution under discussion in this paper.

11 Discussion and conclusions

We have obtained, in this paper, a genuinely new type of charged black holes, with electric and magnetic charges, in the context of a particular class of f(R) modified gravity. We have provided a detailed description of their physical properties, including their stability and causal structure, both in the Jordan and in the Einstein frames. Being more specific, we have worked with the following forms for f(R), namely $f(R)=R+2\beta sqrt{R}$ and $f(R)=R+2\beta \sqrt{R-8\Lambda }$, to produce flat and AdS/dS space-times, respectively, and solved the field equations of f(R) for a spherically symmetric space-time in which $g_{tt}=\frac{1}{g_{rr}}$.⁶ We have solved the resulting field equations in an exact way and derived black holes, which are characterized by three parameters: the mass, which depends on the dimensional parameter $\beta$, bound to have a negative value, and the electric and magnetic charges.

The Ricci scalar of the black holes here found is non-trivial. It has the form $R=\frac{1}{r^2}$, for the case of flat space-time, and $R=\frac{1}{r^2}+8\Lambda$ for the AdS/dS space-times. A most remarkable result is that these black holes cannot be reduced to the ordinary ones appearing in Einstein’s GR; in other words, they are genuinely new black holes of the modified f(R) gravities. We have calculate the scalar invariants of these solutions and shown that the parameter $\beta$ cannot be set equal to zero. The calculations involving the scalar fields have shown that one gets a true singularity at $r=0$. Using conformal transformation, we got charged black hole solutions in the realm of the Einstein frame. An interesting feature of the black holes obtained in this frame is the fact that $g_{tt}\ne \frac{1}{g_{rr}}$, what does not happen for the corresponding black holes in the Jordan frame. However, in spite of the fact that the black holes have different $g_{tt}$ and $g^{rr}$ components for the metric in the Einstein frame, they have coinciding Killing and event horizons.

It is well know that the Jordan and the Einstein frames are mathematically equivalent. To check if their corresponding associated physics are equivalent, too, we have calculated some thermodynamical quantities for the above black holes, respectively obtained in one and in the other frame. A detailed discussion has shown that the physics associated with the entropy, quasi-local energy, and Gibbs free energy, in both frames, turn out to be fully equivalent. However, the physics associated to the Hawking temperature is not the same in both frames: the temperature in the Jordan frame is always positive, contrary to what happens in the Einstein frame, which can lead to negative values of yhe same. This may serve as an indication that the physics of the two frames are not equivalent, at least concerning this important quantity, the black hole temperature. An intriguing conjecture that has come to our minds is the following: could this possibly be related to the loss-of-information paradox?

Going more deeply into the black hole properties, we have studied their stability using linear perturbations. Our calculations show that the radial propagation speed always equals one, in both frames, which means that the constructed black holes are stable. In addition, we have used the procedure of geodesic deviation to study the stability of the black holes, both in the Jordan and in the Einstein frames, and derived in each case the stability condition. Finally, we have also studied the causal structure of our novel black holes. We have shown that, in general, they are not invariant under Lorentz transformations. Moreover, we have identified that there is a (positive or negative) deficit angle associated with them. It goes without saying that the black holes obtained in this work need still to be analyzed in more depth, in order to unveil all of their physical properties, a job we hope to undertake elsewhere. Furthermore, an extension of this study to less symmetric backgrounds and to a more general form of f(R) is pending.

We now consider the possibility that the black hole corresponding to the solution (13) can be found by any observation. The analysis in Section IXB tell that the solution (13) corresponds to $C=\frac{1}{\sqrt{2}}$ in (83) with (84). Because $C=\frac{1}{\sqrt{2}}<1$, the solution makes the deficit angle. Then Figure 17 tells that the black hole generates strong gravitational lensing effects. In the usual black hole, the lensing effects occur only in the region near the black hole but for the geometry expressed by the metric (13) the effects occur in a rather large region, say interstellar region, around the black hole. Therefore the big ring much greater than the standard Einstein ring or double images separated in a large angle could be observed as in the observation of the standard weak lensing as in [89,90,91] in future.

Appendices

Appendix A

The field equations of Ansatz (9) without cosmological constant

Imposing the Ansatz (9) to Eqs. (4), (5) and (7), after using Eq. (10), we get⁷

$$\begin{aligned} \zeta _t{}^t= & {} \frac{1}{4r^{6}\sin ^2\theta \sqrt{{{\mathcal {R}}}^5}}\Big \{4r^2\sqrt{{{\mathcal {R}}}^5} \Big [r^2\sin ^2\theta (rw'+wn_\theta {}^2\nonumber \\&-2ws'n_\theta +q'^2r^2-1 +w\{1+s'^2\})\nonumber \\&+k_\theta {}^2+r^2wp'^2\Big ]+\beta \sin ^2\theta \Big [r^6w{{\mathcal {R}}}w''''\nonumber \\&+3r^6ww'''^2\nonumber \\&-r^3w'''(r^2w''[rw'-12w]+4r^2w'^2\nonumber \\&+2rw'[31w-1]-48w[1-w]) +2r^6w''^3\nonumber \\&-4r^4w''^2(4-6rw'-15w)+2r^2w''(57r^2w'^2\nonumber \\&+14r[3w-5]w'-36w^2+20+16w)+200r^3w'^3\nonumber \\&+4r^2w'^2(96w-85) +8rw'[w-1][27w-23]\nonumber \\&+32[w-1]^2[2w-1]\Big ]\Big \}=0,\end{aligned}$$

(A. 1)

$$\begin{aligned} \zeta _t{}^\theta= & {} \frac{2q'w(n_\theta -s')}{r^2}=0,\qquad \zeta _t{}^\phi = \frac{2q'fp'}{r^2\sin ^2\theta }=0,\nonumber \\ \zeta _r{}^\theta= & {} \frac{2p'k_\theta }{r^4\sin ^2\theta }=0,\qquad \zeta _r{}^\phi =\frac{2(n_\theta -s')k_\theta }{r^4\sin ^2\theta }=0,\end{aligned}$$

(A. 2)

$$\begin{aligned} \zeta _r{}^r= & {} \frac{1}{4r^4\sin ^2\theta \sqrt{{{\mathcal {R}}}^3}}\Big \{4\sqrt{{{\mathcal {R}}}^3}\Big [r^2\sin ^2\theta (rw'-wn_\theta {}^2\nonumber \\&+2ws'n_\theta -ws'^2+[w-1+r^2q'^2])+k'^2 -wr^2p'^2\Big ]\nonumber \\&+\beta \sin ^2\theta \Big (r^2w'''[4w+rw']\nonumber \\&-2r^4w''^2+w''[4r^2(3+w)-16r^3w']-50r^2w'^2\nonumber \\&+4rw'(15-17w)-16(1-3w+2w^2)\Big )\Big \}=0, \end{aligned}$$

(A. 3)

$$\begin{aligned} \zeta _\theta {}^t= & {} 2q'(n_\theta -s')=0,\qquad \zeta _\theta {}^r=\frac{2wk_\theta p'}{r^2\sin ^2\theta },\nonumber \\ \zeta _\theta {}^\phi= & {} \frac{2w(n_\theta -s')p'}{r^2\sin ^2\theta },\qquad \zeta _\phi {}^t=2q'p'=0, \end{aligned}$$

(A. 4)

$$\begin{aligned} \zeta _\phi {}^r= & {} \frac{2w(n_\theta -s')k_\theta }{r^2}=0,\nonumber \\ \zeta _\phi {}^\theta= & {} \frac{2wp'(n_\theta -s')}{r^2}=0, \end{aligned}$$

(A. 5)

$$\begin{aligned} \zeta _\theta {}^\theta= & {} \frac{1}{2r^{6}\sin ^2\theta \sqrt{{{\mathcal {R}}}^5}}\Big \{2r^2\sqrt{{{\mathcal {R}}}^5}\Big [r^2\sin ^2\theta \Big (\frac{r^2w''}{2}\nonumber \\&+rw'-wn_\theta {}^2+2wn_\theta s'-q'^2r^2-ws'^2\Big )\nonumber \\&-k_\theta {}^2+2l_\phi k_\theta +r^2wp'^2\Big ]-\beta \sin ^2\theta \Big [r^6w{{\mathcal {R}}}w''''\nonumber \\&+\frac{3r^6ww'''^2}{2}-r^3w'''(r^2w''[rw'-7w]+4r^2w'^2\nonumber \\&+2rw'[14w-1]-22w[1-w])+2r^6w''^3\nonumber \\&-2r^4w''^2\Big (5-9rw'-18w\Big )+2r^2w''(33r^2w'^2\nonumber \\&+r[27w-34]w'-18w^2+8+10w)]+104r^3w'^3\nonumber \\&+2r^2w'^2(81w-74)+4rw'[15w-16][w-1]\nonumber \\&-4(2-8w+10w^2-4w^3)\Big \}=0, \end{aligned}$$

(A. 6)

$$\begin{aligned} \zeta _\phi {}^\phi= & {} \frac{1}{2r^{6}\sin ^2\theta \sqrt{{{\mathcal {R}}}^5}}\Big \{2r^2\sqrt{{{\mathcal {R}}}^5} \Big [r^2\sin ^2\theta \Big (\frac{r^2w''}{2}\nonumber \\&+rw'+wn_\theta {}^2-2wn_\theta s'-q'^2r^2+ws'^2\Big )\nonumber \\&-k_\theta {}^2-r^2wp'^2\Big ]-\beta \sin ^2\theta \Big [r^6w{{\mathcal {R}}}w''''\nonumber \\&+\frac{3r^6ww'''^2}{2}-r^3w'''(r^2w''[rw'-7w]\nonumber \\&+4r^2w'^2+2rw'[14w-1]-22w[1-w])+2r^6w''^3\nonumber \\&-2r^4w''^2\Big (5-9rw'-18w\Big )+2r^2w''(33r^2w'^2\nonumber \\&+r[27w-34]w'-18w^2+8+10w)]+104r^3w'^3\nonumber \\&+2r^2w'^2(81w-74)+4rw'[15w-16][w-1]\nonumber \\&-4(2-8w+10w^2-4w^3)\Big \}=0, \end{aligned}$$

(A. 7)

$$\begin{aligned} \zeta= & {} \frac{1}{2r^{6}\sqrt{{{\mathcal {R}}}^5}}\Big \{2r^6\sqrt{{{\mathcal {R}}}^5}\nonumber \\&-3\beta \Big [r^6w{{\mathcal {R}}}w''''+\frac{3r^6ww'''^2}{2}\nonumber \\&-r^3w'''(r^2w''[rw'-6w]+4r^2w'^2\nonumber \\&+2rw'[31w-1]-24w[1-w])+2r^6w''^3\nonumber \\&-2r^4w''^2\Big (6-10rw'-17w\Big )+2r^2w''(41r^2w'^2\nonumber \\&+2r[16w-23]w'-16w^2+12+4w)\nonumber \\&+136r^3w'^3+2r^2w'^2(117w-106)\nonumber \\&+8rw'[15w-13][w-1]\nonumber \\&+16(2w-1)(w-1)^2\Big ]\Big \}=0, \end{aligned}$$

(A. 8)

where⁸ q(r), $n(\theta )$, s(r), $l(\phi )$, p(r), and $k(\theta )$ are the gauge potentials, defined as

$$\begin{aligned} \xi :=q(r)dt+ n(\theta )dr+s(r)d\theta +[p(r)+k(\theta )]d\phi . \end{aligned}$$

(A. 9)

For brevity, we put $w'=\frac{dw}{dr}$, $w''=\frac{d^2w}{dr^2}$, $w'''=\frac{d^3w}{dr^3}$, $w''''=\frac{d^4w}{dr^4}$, $q'=\frac{dq}{dr}$, $s'=\frac{ds}{dr}$, $p'=\frac{dm}{dr}$ $n_\theta =\frac{dn}{d\theta }$ and $k_\theta =\frac{dk}{d\theta }$. We must note that, when the magnetic fields vanish, i.e. $n=s=p=k=0$, we get $\zeta _\theta {}^\theta =\zeta _\phi {}^\phi$, and in this case the field Eqs. (A. 1) $\sim$ (A. 8) coincides with the one derived in [58].

Appendix B

The field equations of Ansatz (9) with cosmological constant

Now

$$\begin{aligned} \zeta _t{}^t= & {} \frac{1}{4r^{9}\sin ^2\theta \sqrt{{\text {R}}^5}}\Big \{4r^5\sqrt{{\text {R}}^5}\Big [r^2\sin ^2\theta (rw'+wn_\theta {}^2\nonumber \\&-2ws'n_\theta +q'^2r^2-1+2r^2\Lambda +w\{1+s'^2\})\nonumber \\&+k_\theta {}^2+r^2+wp'^2\Big ]+\beta \sin ^2\theta \Big [r^6w{\text {R}}w''''\nonumber \\&+3r^6ww'''^2-r^3w'''(r^2w''[rw'-12w]+4r^2w'^2\nonumber \\&+2rw'[31w-1+4r^2\Lambda ]+48w[1-w-2r^2\Lambda ])\nonumber \\&+2r^6w''^3-4r^4w''^2\Big (4-6rw'-15w\nonumber \\&-16r^2\Lambda \Big )+2r^2w''(57r^2w'^2+14r[3w-5+8r^2\Lambda ]w'\nonumber \\&-36w^2+80[4r^2\Lambda -1]^2+16w[1+9r^2\Lambda ])\nonumber \\&+200r^3w'^3+4r^2w'^2\Big (96w-85\nonumber \\&+324r^2\Lambda \Big )+8rw'\Big \{27w^2-23\nonumber \\&+ 2w(47r^2\Lambda -50)+11w^3+5w^2(1-2r^2\Lambda )\nonumber \\&+w(2+24r^4\Lambda ^2-11r^2\Lambda )+(4r^2\Lambda -1)^3\Big \}\Big ]\Big \}=0, \end{aligned}$$

(B. 1)

$$\begin{aligned}&\zeta _t{}^\theta =\frac{2q'w(n_\theta -s')}{r^2}=0,\qquad \zeta _t{}^\phi =2q'wp'=0,\nonumber \\&\zeta _r{}^\theta =2p'k_\theta =0,\qquad \zeta _r{}^\phi =\frac{2(n_\theta -s')k_\theta }{r^4\sin ^2\theta }=0, \end{aligned}$$

(B. 2)

$$\begin{aligned}&\zeta _r{}^r=\frac{1}{2r^7\sin ^2\theta \sqrt{{\text {R}}^3}}\Big \{r \sqrt{{\text {R}}^3}\Big [r^2\sin ^2\theta (rw'-wn_\theta {}^2\nonumber \\&+2ws'n_\theta -ws'^2+r^2q'+w-1+2r^2\Lambda )\nonumber \\&+k_\theta {}^2-r^2+wp'^2\Big ]\nonumber \\&+\beta \sin ^2\theta r^3\Big [r^3w'''\Big (4w+rw'\Big )\nonumber \\&-2r^4w''^2+4r^2w''(12r^2\Lambda -3-w+4rw')\nonumber \\&-50r^2w'^2-4rw'(56r^2\Lambda -15+17w)\nonumber \\&-32w^2+16w(3-16r^2\Lambda ) \nonumber \\&+16(1-4r^2\Lambda )^2\Big ]\Big \}=0, \end{aligned}$$

(B. 3)

$$\begin{aligned} \zeta _\theta {}^t= & {} 2q'(n_\theta -s')=0,\qquad \zeta _\theta {}^r=\frac{2w(l_\phi -k_\theta )p'}{r^2\sin ^2\theta }=0,\nonumber \\ \zeta _\theta {}^\phi= & {} \frac{2w(n_\theta -s')p'}{r^2\sin ^2\theta }=0,\qquad \zeta _\phi {}^t=2q'p'=0, \end{aligned}$$

(B. 4)

$$\begin{aligned} \zeta _\phi {}^r= & {} \frac{2w(n_\theta -s')k_\theta }{r^2}=0,\nonumber \\ \zeta _\phi {}^\theta= & {} \frac{2wp'(n_\theta -s')}{r^2}=0, \end{aligned}$$

(B. 5)

$$\begin{aligned} \zeta _\theta {}^\theta= & {} \frac{1}{2r^9\sin ^2\theta \sqrt{{\text {R}}^5}}\Big \{4r^5 \sqrt{{\text {R}}^5}\Big [r^2\sin ^2\theta (r^2w''+2rw'\nonumber \\&-2wn_\theta {}^2+4ws'n_\theta -2ws'^2\nonumber \\&-2r^2q'^2+4r^2\Lambda )-2k_\theta {}^2+2r^2+2wp'^2\Big ]\nonumber \\&-\beta \sin ^2\theta \Big [3r^6ww'''^2-4r^6ww''''{\text {R}}\nonumber \\&-4r^3w'''([rw'-7w]r^2w''+4r^2w'^2\nonumber \\&+2rw'[4r^2\Lambda -1+14w]\nonumber \\&+2w[11w+20r^2\Lambda -11])\nonumber \\&+8r^6w''^3+8r^4w''^2[9rw'+18w-5+24r^2\Lambda ]\nonumber \\&+8r^2w''\Big (33r^2w'^2+rw'[32r^2\Lambda -34+27w]\nonumber \\&-18w^2+2w[5+33r^2\Lambda ]\nonumber \\&+4[1-10r^2\Lambda +24r^4\Lambda ^2]\Big )\nonumber \\&+208r^3w'^3+8r^2w'^2[81w-74+328r^2\Lambda ]\nonumber \\&+32rw'(15w^2+w[156r^2\Lambda -31]\nonumber \\&+8[2+82r^4\Lambda ^2-19r^2\Lambda ])\nonumber \\&+32w^3+32w^2[8r^2\Lambda -5]-64w(6r^2\Lambda -1\nonumber \\&-20r^4\Lambda ^2)+32(1-4r^2\Lambda )^2(8r^2\Lambda -1)\Big ]\Big \}=0, \end{aligned}$$

(B. 6)

$$\begin{aligned} \zeta _\phi {}^\phi= & {} \frac{1}{2r^9\sin ^2\theta \sqrt{{\text {R}}^5}}\Big \{4r^5 \sqrt{{\text {R}}^5}\Big [r^2\sin ^2\theta (r^2w''+2rw'\nonumber \\&+2wn_\theta {}^2-4ws'n_\theta +2ws'^2-2r^2q'^2\nonumber \\&+4r^2\Lambda )-2k_\theta {}^2-2r^2+2wp'^2\Big ]\nonumber \\&-\beta \sin ^2\theta \Big [3r^6ww'''^2-4r^6ww''''{\text {R}}\nonumber \\&-4r^3w'''([rw'-7w]r^2w''+4r^2w'^2\nonumber \\&+2rw'[4r^2\Lambda -1+14w]\nonumber \\&+2w[11w+20r^2\Lambda -11])\nonumber \\&+8r^6w''^3+8r^4w''^2[9rw'+18w-5\nonumber \\&+24r^2\Lambda ]+8r^2w''(33r^2w'^2\nonumber \\&+rw'[32r^2\Lambda -34+27w]\nonumber \\&-18w^2+2w[5+33r^2\Lambda ]\nonumber \\&+4[1-10r^2\Lambda +24r^4\Lambda ^2])+208r^3w'^3\nonumber \\&+8r^2w'^2[81w-74+328r^2\Lambda ]\nonumber \\&+32rw'(15w^2+w[156r^2\Lambda -31]\nonumber \\&+2[8+321r^4\Lambda ^2-76r^2\Lambda ])\nonumber \\&+32w^3+32w^2[8r^2\Lambda -5]-64w(6r^2\Lambda -1\nonumber \\&-20r^4\Lambda ^2)+32(1-4r^2\Lambda )^2(8r^2\Lambda -1)\Big ]\Big \}=0, \end{aligned}$$

(B. 7)

$$\begin{aligned} \zeta= & {} \frac{1}{4r^6\sqrt{{\text {R}}^5}}\Big \{4r^6 \sqrt{{\text {R}}^7}\nonumber \\&+\beta \Big [6r^6{\text {R}}ww''''+9r^6ww'''^2\nonumber \\&-6r^3w'''([rw'-6w]r^2w''\nonumber \\&+4r^2w'^2+2rw'[4r^2\Lambda -1+16w]\nonumber \\&+24w[w-1+2r^2\Lambda ])+12r^6w''^3\nonumber \\&+4r^4w''^2[30rw'+51w-18+80r^2\Lambda ]\nonumber \\&+4r^2w''(123r^2w'^2+22rw'[296r^2\Lambda -69+48w]-48w^2\nonumber \\&+4w[3+74r^2\Lambda ]+4[9-80r^2\Lambda \nonumber \\&+176r^4\Lambda ^2])+816r^3w'^3\nonumber \\&+4r^2w'^2[351w-318+1304r^2\Lambda ]\nonumber \\&+16rw'(45w^2+w[344r^2\Lambda -84]+39\nonumber \\&+704r^4\Lambda ^2-332r^2\Lambda )+192w^3\nonumber \\&+32w^2[34r^2\Lambda -15]-64w(37r^2\Lambda -6\nonumber \\&-88r^4\Lambda ^2)+32(1-4r^2\Lambda )^2(16r^2\Lambda -3)\Big ]\Big \}=0. \end{aligned}$$

(B. 8)