1 Introduction

The Standard Model (SM) has been experimentally verified with high accuracy and very successful. In the SM, the Higgs field plays a role in the mass generation of particles. The potential for the Higgs field is given to break the electroweak (EW) symmetry, and particle masses are originated from the non-vanishing vacuum expectation value (VEV). This mechanism has been tested by the EW precision observables, the 125-GeV Higgs measurements, and so on, and the predictions correspond reasonably well with the experimental results. This success, however, poses a question about the origin of the Higgs potential. In particular, the mass squared of the Higgs field is negative and requires a severe fine-tuning to cancel the very large radiative corrections. In order to avoid the fine-tuning, many models beyond the SM have been proposed so far; e.g., supersymmetry, composite Higgs, little Higgs, top partner, extra dimensions, and gauge-Higgs unification. These extended models generally predict additional particles around TeV scale, that can be tested in the experiments at the large hadron collider (LHC). Among the new particles, additional scalar fields are often suggested as good candidates to validate the models. The additional scalars, therefore, have been studied widely in both model-dependent and model-independent ways.

Interestingly, such a new particle, that interacts with the SM particles through the weak interaction and/or Yukawa interactions, can still take mass of \({\mathcal {O}}(100)\,\text {GeV}\) [1, 2], if the couplings with light quarks and leptons are suppressed. The possibility of an additional scalar boson lighter than the 125 GeV Higgs still remains. Recently, the CMS collaboration has reported a new excess in the di-tau final states within all the \(\tau \) decay modes (leptonic and hadronic) by using the Run 2 full data [3], which is an extension of the previous searches [4,5,6,7,8,9]. The excess can be interpreted as a resonance of a new particle. The local and global significance of the excess are \(2.6\sigma \) and \(2.3\sigma \) at the invariant mass of \(m_{\tau \tau }=95\,\text {GeV}\), respectively.Footnote 1 At \(m_{\tau \tau }=100\,\text {GeV}\), these values are \(3.1\sigma \) and \(2.7\sigma \). By introducing an additional single neutral narrow resonance \(\phi \), the best fit values for the excess are [3]

$$\begin{aligned}&\sigma (gg \rightarrow \phi )\times \textrm{BR}(\phi \rightarrow \tau {\bar{\tau }}) = 7.7^{+3.9}_{-3.1}~\textrm{pb}\nonumber \\&\qquad \text {for }m_{\phi } = 95\,\text {GeV}, \end{aligned}$$
(1)

or

$$\begin{aligned}&\sigma (gg \rightarrow \phi )\times \textrm{BR}(\phi \rightarrow \tau {\bar{\tau }}) = 5.8^{+2.4}_{-2.0}~\textrm{pb}\nonumber \\&\qquad \text {for }m_{\phi } = 100\,\text {GeV}. \end{aligned}$$
(2)

These cross sections are comparable to the \(125\,\text {GeV}\) SM Higgs boson, h [11],

$$\begin{aligned} \sigma (gg \rightarrow h)\times \textrm{BR}(h \rightarrow \tau {\bar{\tau }}) = 3.1\pm 0.2~\textrm{pb}. \end{aligned}$$
(3)

Note that there is no excess in the b-tagging category, which implies that the b-associated \(\phi \) production is disfavored.

Interestingly, in the same mass region, a different excess has also been reported in the di-photon final states by the CMS collaboration based on the full Run 1 [12] and the first Run 2 (35.9 \(\hbox {fb}^{-1}\)) data [13]. The local and global significance are \(2.8\sigma \) and \(1.3\sigma \) at \(m_{\gamma \gamma } = 95.3\,\text {GeV}\). This excess can be interpreted as a new resonance, \(\phi \), that decays to two photons, i.e., \(gg \rightarrow \phi \rightarrow \gamma \gamma \) (see Eq. (31)). Although the similar analysis has been performed by the ATLAS collaboration [14], the sensitivity is not good enough to check the consistency [15]. Moreover, another mild excess has been reported in the LEP experiment, that can be interpreted as \(e^+e^+\rightarrow Z \phi \rightarrow Z b\bar{b}\) [16]. The signal corresponds to \(2.3\sigma \) local significance at \(m_\phi =98\,\text {GeV}\). Therefore, it is very interesting to consider the possibility that these excesses are caused by the same new particle \(\phi \). A variety of new physics interpretations have been discussed in Refs. [17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32] focusing on the CMS di-photon and the LEP \(b\bar{b}\) excesses, while in Refs. [33, 34] including the CMS di-tau excess as well.

Fig. 1
figure 1

Representative Feynman diagrams for a narrow resonance \(\phi \) exchange in the gluon fusion (\(gg \rightarrow \tau \bar{\tau }\)) and the top-quark associated processes (\(gg \rightarrow t \bar{t} + \tau {\bar{\tau }}\))

Full size image

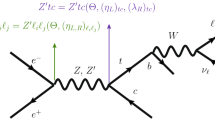
In this paper, we point out that associated production of \(\phi \) with two top quarks can provide a simple and powerful way to verify the di-tau excess in Eqs. (1) and (2). In Fig. 1, the relevant diagrams for \(gg \rightarrow \tau {\bar{\tau }}\) and \(gg\rightarrow t\bar{t}+\tau \bar{\tau }\) are shown. As shown Eq. (3), the di-tau excess requires the new resonance cross section almost comparable to the SM Higgs boson via the gluon fusion. The \(\tau \bar{\tau }\) resonance at 95–\(100\,\text {GeV}\), however, suffers from the huge Z boson background which stems from the tree-level Drell–Yan (DY) process. Such a Z peak pollution will be mild when the top-quark associated production is selected. This is because that the production cross section of \(t\bar{t}+Z\) and \(t\bar{t}+h\) are the same size in the SM (see Sect. 2.1 for the explicit numbers), and furthermore, the new resonance is produced by the tree level, which could amplify the sensitivity to probe the new resonance. We will investigate the LHC sensitivity to the possible 95–\(100\,\text {GeV}\) resonance in the top-associated process.

In Sect. 2, we introduce the minimal setup to account for the \(\tau \bar{\tau }\) excess and summarize the predictions of the top-associated productions. In Sect. 3, the numerical analysis to derive the upper limits on the model-independent \(t\bar{t}+\tau \bar{\tau }\) cross section is performed for the new resonance. Section 4 is devoted to summary and discussion.

2 Setup

In this section, we introduce a simplified model that can account for the excesses in the 95–\(100\,\text {GeV}\) region. We introduce an additional scalar boson which has large couplings with top and \(\tau \), since the gluon fusion is dominated by the chiral heavy fermion loop [35] and the resonance preferentially decays into \(\tau \) leptons. It is noted that no excess is found with \(\tau {\bar{\tau }}\) resonant events in association with b quark jets [3], so that a coupling with b is unlikely to be large. There are several ways to derive such a scalar effectively at low energy. In this study, we do not specify models and simply assume that extra neutral scalars, H and A, couple to top and \(\tau \) as follows:

$$\begin{aligned} -{\mathcal {L}}_\textrm{eff} =\! \frac{\rho _{tt}^H}{\sqrt{2}}\,\bar{t} H t \!+\!\frac{\rho _{\tau \tau }^H}{\sqrt{2}}\,\bar{\tau } H \tau \pm i \frac{\rho _{tt}^A}{\sqrt{2}}\,\bar{t} A \gamma _5 t+i \frac{\rho _{\tau \tau }^A}{\sqrt{2}}\,\bar{\tau } A \gamma _5 \tau . \end{aligned}$$
(4)

The all couplings, \(\rho ^\phi _{tt}\) and \(\rho ^\phi _{\tau \tau }\) (\(\phi =H, \, A\)), are real in our study. Then, H (A) corresponds to a CP-even (CP-odd) scalar.Footnote 2 As we will see, the \(\gamma _5\) structure plays an important role in our analysis. Note that the relative sign for the A interaction depends on the UV theory. In our study, this relative sign does not affect the conclusion.

The possible UV completion of the light scalar boson could be the Two-Higgs-Doublet Model (2HDM) with a real singlet scalar [23, 27, 29, 30, 33, 34], flavor-aligned 2HDM [38], Generic 2HDM (G2HDM, type-III 2HDM) [39, 40], axion-like particle (ALP) [41], NMSSM [42] and so on.Footnote 3 If one takes a G2HDM as an illustrative model, the oblique corrections and the LHC constraint on a charged scalar [43, 44] do not allow to set both H and A masses around \(100\,\text {GeV}\) for the \(\tau \bar{\tau }\) excess. In this paper we do not discuss the detailed setup and consider the two cases that either H or A resides around 100 GeV. We comment on the other couplings except for the effective Lagrangian in Eq. (4), which exist in the UV completed models in general. We suppose only that the gluon-fusion of \(\phi \) is dominated in the top-quark loop contribution, which would be correct when the coupling to the bottom quark is not comparable to the top one. Then, a correlation between two cross sections, \(\sigma (pp \rightarrow gg \rightarrow \phi \rightarrow \tau \bar{\tau })\) and \(\sigma (pp \rightarrow t\bar{t} +\phi \rightarrow t\bar{t}+\tau {\bar{\tau }})\), becomes robust and is independent of the \(\phi \)’s decay modes with the other interactions not presented in Eq. (4) (including dark sectors).

2.1 CP-even scalar scenario

First, we consider the case that the resonance reported by the CMS collaboration is a CP-even scalar H. The gluon fusion production cross section of H at \(\sqrt{s}=13\,\text {TeV}\) is predicted as follows

$$\begin{aligned}&\sigma (pp\rightarrow gg\rightarrow H)= 87.2 \,(\rho _{tt}^H)^2~\textrm{pb}\quad \mathrm{{for}}~ m_H=95\,\text {GeV}, \end{aligned}$$
(5)
$$\begin{aligned}&\sigma (pp\rightarrow gg\rightarrow H)= 79.5 \, (\rho _{tt}^H)^2~\textrm{pb}\quad \mathrm{{for}}~ m_H=100\,\text {GeV}, \end{aligned}$$
(6)

which are evaluated by SusHi v1.7.0  [45, 46] at next-to-next-to leading order (NNLO).Footnote 4 The di-tau excess in Eqs. (1) and (2) can be accommodated by

$$\begin{aligned}&\rho _{tt}^H \sqrt{\textrm{BR}(H \rightarrow \tau {\bar{\tau }})} = 0.30\pm 0.07 \quad \mathrm{{for}}~ m_H=95\,\text {GeV}, \end{aligned}$$
(7)
$$\begin{aligned}&\rho _{tt}^H \sqrt{\textrm{BR}(H \rightarrow \tau {\bar{\tau }})} = 0.27\pm 0.05 \quad \mathrm{{for}}~ m_H=100\,\text {GeV}. \end{aligned}$$
(8)

We find that \(\rho ^H_{tt}\) is sizable to explain the excess: \(\rho ^H_{tt} \gtrsim 0.22\).

The \(\rho _{tt}^H\) interaction also contributes to the production of \(\phi \) in association with two top quarks, as shown in the middle and right diagrams in Fig. 1. The production cross section at \(\sqrt{s}=13\,\text {TeV}\) is obtained as

$$\begin{aligned}&\sigma (pp\rightarrow t\bar{t}+ H)= 1.07\,(\rho _{tt}^H)^2~\textrm{pb}\quad \mathrm{{for}}~ m_H=95\,\text {GeV}, \end{aligned}$$
(9)
$$\begin{aligned}&\sigma (pp\rightarrow t\bar{t}+ H)= 0.94\,(\rho _{tt}^H)^2~\textrm{pb}\quad \mathrm{{for}}~ m_H=100\,\text {GeV}, \end{aligned}$$
(10)

at next-to leading order (NLO). Here, we evaluate the production cross section at the leading order by MadGraph5_aMC@NLO [47] and multiply the NLO K factor of 1.29 for simplicity [48].

Combining the above results, the explanation of the excess predicts a sizable cross section of \(pp \rightarrow t\bar{t} H \rightarrow t\bar{t} + \tau \bar{\tau }\):

$$\begin{aligned}&\sigma (pp\rightarrow t\bar{t}+ H)\times \textrm{BR}(H \rightarrow \tau {\bar{\tau }})\nonumber \\&\qquad =[0.056,0.094,0.14]~\textrm{pb}\quad \mathrm{{for}}~ m_H=95\,\text {GeV}, \end{aligned}$$
(11)
$$\begin{aligned}&\sigma (pp\rightarrow t\bar{t}+ H)\times \textrm{BR}(H \rightarrow \tau {\bar{\tau }}) \nonumber \\&\qquad =[0.045,0.069,0.097]~\textrm{pb}\quad \mathrm{{for}}~ m_H=100\,\text {GeV}, \end{aligned}$$
(12)

where numbers in parentheses indicate the \(1\sigma \) range with its central value.

The top-associated production cross section of the SM Higgs boson has been measured with 79.8 \(\hbox {fb}^{-1}\) of the Run 2 data [49]: \(\sigma (pp\rightarrow t\bar{t} + h)=0.67\pm 0.14\,\textrm{pb}\). This is consistent with the SM prediction, \(\sigma (pp\rightarrow t\bar{t}+h)_\textrm{SM}=0.51\,\textrm{pb}\). Combining the subsequent decay branching ratio of \(\textrm{BR}(h\rightarrow \tau {\bar{\tau }})_\textrm{SM}\sim 6\%\), \(\sigma (pp\rightarrow t\bar{t} + h)_\textrm{SM} \times \textrm{BR}({h\rightarrow \tau {\bar{\tau }}})_\textrm{SM} \simeq 0.03\,\textrm{pb}\) is derived in the SM, and thus the predicted cross section of H is larger than the SM Higgs by a factor of approximately three.

We comment on the top-associated Z production cross section. It has been measured based on the full Run 2 data [50]; \(\sigma (pp\rightarrow t\bar{t}+Z)=0.99\pm 0.09\,\textrm{pb}\).Footnote 5 This result is also consistent with the SM prediction, \(\sigma (pp\rightarrow t\bar{t}+Z)_\textrm{SM} = 0.84^{+0.09}_{-0.10}\,\textrm{pb}\) at NLO QCD and EW accuracy [51]. Since \(\textrm{BR}(Z\rightarrow \ell \bar{\ell })\) is about \(3\%\), we obtain \(\sigma (pp\rightarrow t\bar{t}+Z)\times \textrm{BR}(Z\rightarrow \tau {\bar{\tau }}) \simeq 0.03\,\textrm{pb}\), that is comparable to the top-associated production of h.

2.2 CP-odd scalar scenario

Next, we consider the CP-odd scalar A interpretation. The analysis in Sect. 2.1 is applied to this case, replacing H with A. The sizes of the cross sections are, however, different because of the couplings in Eq. (4), so that the predictions are totally different.

The gluon fusion cross section of A at \(\sqrt{s}=13\,\text {TeV}\) is

$$\begin{aligned}&\sigma (pp\rightarrow gg\rightarrow A)= 201.7\,(\rho _{tt}^A)^2\,\textrm{pb}\quad \mathrm{{for}}~ m_A=95\,\text {GeV}, \end{aligned}$$
(13)
$$\begin{aligned}&\sigma (pp\rightarrow gg\rightarrow A)= 184.4\,(\rho _{tt}^A)^2\,\textrm{pb}\quad \mathrm{{for}}~ m_A=100\,\text {GeV}, \end{aligned}$$
(14)

at NNLO [45, 46]. Assuming \(\rho ^H_{tt}=\rho ^A_{tt}\), these predictions are twice as large as them in the H case due to the different \(\gamma _5\) structure in the top-quark loop. The di-tau excess in Eqs. (1) and (2) can be accommodated by

$$\begin{aligned}&\rho _{tt}^A \sqrt{\textrm{BR}(A \rightarrow \tau {\bar{\tau }})} = 0.20\pm 0.04 \quad \mathrm{{for}}~ m_A=95\,\text {GeV}, \end{aligned}$$
(15)
$$\begin{aligned}&\rho _{tt}^A \sqrt{\textrm{BR}(A \rightarrow \tau {\bar{\tau }})} = 0.18\pm 0.03 \quad \mathrm{{for}}~ m_A=100\,\text {GeV}. \end{aligned}$$
(16)

The production cross section of the top-associated production is

$$\begin{aligned}&\sigma (pp\rightarrow t \bar{t}+ A)=0.30\,(\rho _{tt}^A)^2\,\textrm{pb}\quad \mathrm{{for}}~ m_A=95\,\text {GeV}, \end{aligned}$$
(17)
$$\begin{aligned}&\sigma (pp\rightarrow t\bar{t}+ A)=0.29\,(\rho _{tt}^A)^2\,\textrm{pb}\quad \mathrm{{for}}~ m_A=100\,\text {GeV}, \end{aligned}$$
(18)

where the same NLO K factor as in the CP-even scalar production is assumed [52]. In Ref. [52], it has been shown that the NLO K-factors are almost independent of the CP-even/odd and the mass. In contrast to the gluon fusion cross section, the results are three times as small as them in the H case when \(\rho ^H_{tt}=\rho ^A_{tt}\), as shown in Eqs. (9) and (10). This is again originated from the \(\gamma _5\) structure. There is a destructive interference between the contribution of the middle diagram and that of the right diagram in Fig. 1 [52,53,54].

As a result, the cross section of \(pp\rightarrow t\bar{t}+A \rightarrow t\bar{t} + \tau \bar{\tau }\), that is consistent with the di-tau excess, is predicted to be smaller than that of the H case:

$$\begin{aligned}&\sigma (pp\rightarrow t\bar{t}+ A) \times \textrm{BR}(A \rightarrow \tau {\bar{\tau }})\nonumber \\&\qquad =[0.007,0.011,0.017]\,\textrm{pb}\quad \mathrm{{for}}~ m_A=95\,\text {GeV}, \end{aligned}$$
(19)
$$\begin{aligned}&\sigma (pp\rightarrow t\bar{t}+ A)\times \textrm{BR}(A \rightarrow \tau {\bar{\tau }})\nonumber \\&\qquad =[0.005,0.009,0.013]\,\textrm{pb}\quad \mathrm{{for}}~ m_A=100\,\text {GeV}. \end{aligned}$$
(20)

It is also known that the angular correlation and transverse momentum distributions of \(pp\rightarrow t\bar{t}+A\) are different from \(pp\rightarrow t\bar{t}+H\) due to the presence of \(\gamma _5\) in Eq. (4) [54].

Fig. 2
figure 2

The histograms of the additional resonance \(\phi \) (blue) and SM Higgs (red) event shapes are shown with the experimental data (cross) and their uncertainties (dashed band). The left panel is for the boosted \(\tau _{h}\tau _{h}\) and the right panel is the \(tt(0\ell ) + \tau _\textrm{h}\tau _\textrm{h}\) categories, respectively. The signal normalization is assumed to be \(\mu _\phi =2\), and \(m_\phi =95\,\)GeV are set for the mass. See the text for details

Full size image

3 Comparisons to the ATLAS data

In this section, we compare the CMS di-tau excesses in Eqs. (1) and (2) to the ATLAS results that involve \(\tau \bar{\tau }\) in the final states. Since the range of the ATLAS data set for the exotic particle search decaying to \(\tau \bar{\tau }\) is \(m_{\tau \tau }\ge 200\,\text {GeV}\) [10], the 95–\(100\,\text {GeV}\) region has not been covered. Instead, we utilize the ATLAS Run 2 full data for the \(h \rightarrow \tau {\bar{\tau }}\) decay channel where h is the SM Higgs boson [55]. The \(h\rightarrow \tau \bar{\tau }\) and \(Z\rightarrow \tau \bar{\tau }\) events have been carefully studied by using the several production processes. Therefore the additional narrow resonance \(\phi \) that decays to \(\tau \bar{\tau }\) can also be probed. In the following, we analyze the data in the boosted \(\tau _\textrm{h} \tau _\textrm{h}\) and \(tt(0\ell ) + \tau _\textrm{h} \tau _\textrm{h}\) categories [55], where \(\tau _\textrm{h}\) denotes \(\tau \) that decays hadronically.

3.1 Boosted \(\tau \bar{\tau }\) search

The boost categories defined in Ref. [55] consist of the events that fail to meet the criteria of the vector-boson fusion (VBF), vector-boson associated production (VH), and a pair of top-quark associated production. The events have high-\(p_\textrm{T}\) (boosted) Higgs candidates. The more than \(70 \%\) events, actually, come from the gluon fusion with large Higgs boson transverse momentum in the analysis of Ref. [55]. Hence, the ATLAS data in this category should be a good comparison to the CMS di-tau excess. We use the result in the boost_2 category corresponding to \(200< p_\textrm{T}^{\tau \tau } < 300\,\text {GeV}\) in Ref. [55].Footnote 6

Using the the narrow width approximation, we define a signal strength for the gluon fusion of \(\phi \),

$$\begin{aligned} \mu _\phi (\tau {\bar{\tau }}) \equiv \frac{\sigma (pp\rightarrow gg \rightarrow \phi )\times \textrm{BR}(\phi \rightarrow \tau {\bar{\tau }})}{\sigma (pp\rightarrow gg \rightarrow h)_\mathrm{{SM}}\times \textrm{BR}(h\rightarrow \tau {\bar{\tau }})_\mathrm{{SM}}}, \end{aligned}$$
(21)

where the denominator is values of the \(125\,\text {GeV}\) SM Higgs. In the left panel of Fig. 2, an expected histogram of the \(\phi \) with \(m_{\phi }=95\,\text {GeV}\) and \(\mu _{\phi }(\tau \bar{\tau })=2\) is shown by the blue shaded region. Here the SM Background (Bkg), except for the SM Higgs boson, is subtracted from the data which corresponds to the bottom-left panel of Fig. 20 (boost_2 category) of Ref. [55]. Note that the SM Higgs histogram (red shaded region) stands for \(pp \rightarrow h \rightarrow \tau \bar{\tau }\) and is scaled by 1/0.93 from the original figure.Footnote 7 The \(0.93\,(^{+0.13}_{-0.12})\) is a global fit result of the signal strength of \(p p \rightarrow h \rightarrow \tau \bar{\tau }\) [55]. The dashed band represents the total uncertainty of the SM Bkg. It is shown that there is a huge uncertainty around \(m_{\tau \tau }=80\)–\(100\,\text {GeV}\), which comes from the DY (boosted) Z-boson production.

By using a \(\chi ^2\) test which will be explicitly defined in the next section, we set \(95\%\) confidence level (CL) upper limits on the signal strength,

$$\begin{aligned}&\mu _\phi (\tau {\bar{\tau }}) < 3.78 \quad \text {for }m_{\phi } = 95\,\text {GeV}, \end{aligned}$$
(22)
$$\begin{aligned}&\mu _\phi (\tau {\bar{\tau }}) < 3.61 \quad \text {for }m_{\phi } = 100\,\text {GeV}, \end{aligned}$$
(23)

or equivalently, the upper limits on the production cross sections,

$$\begin{aligned}&\sigma (gg \rightarrow \phi )\times \textrm{BR}(\phi \rightarrow \tau {\bar{\tau }}) < 11.5 \,\textrm{pb}\quad \! \text {for }m_{\phi } = 95\,\text {GeV}, \end{aligned}$$
(24)
$$\begin{aligned}&\sigma (gg \rightarrow \phi )\times \textrm{BR}(\phi \rightarrow \tau {\bar{\tau }}) < 11.0 \,\textrm{pb}\quad \! \text {for }m_{\phi } =\! 100\,\text {GeV}\!. \end{aligned}$$
(25)

We find that the ATLAS data in the boosted \(\tau _\textrm{h}{\tau }_\textrm{h}\) category are consistent with the CMS di-tau excess in Eqs. (1) and (2) even if the upper edge of the 1\(\sigma \) is considered.

3.2 \(t\bar{t}+\tau \bar{\tau }\) search

In this section, we compare the CMS di-tau excess with the ATLAS data in the \(tt(0\ell ) + \tau _\textrm{h} \tau _\textrm{h}\) category [55]. Due to the limited statistics, the ATLAS collaboration has not performed a serious top reconstruction, but just imposed either six jets including at least one b-tagged jet or five jets including at least two b-tagged jets for the event selection.

As mentioned in Sect. 1, the additional \(t\bar{t}\) requirement is expected to improve the sensitivity to probe the new resonance, because the huge DY Z-boson Bkg can be vetoed and the production cross sections of \(t\bar{t} + \{h,Z,\phi \} \rightarrow t\bar{t} + \tau \bar{\tau }\) are of the same size. However, since the top-quark tagging has not been seriously imposed in this ATLAS data, the SM Bkg is still dominated by the DY process (\(pp \rightarrow Z+5-6\,\)QCD jets), and still large Bkg remains even in the signal region (\(m_{\tau \tau }\simeq 125\,\text {GeV}\)), as one can see in Fig. 11 of Ref. [55]. The region of interest in this paper is \(m_{\tau \tau }=95\)–\(100\,\text {GeV}\), and hence we have the large Bkg from \(Z\rightarrow \tau \bar{\tau }\). Nonetheless, we use this result to derive the current experimental limit on the new resonance production. It is naively expected that a severe top-quark tagging algorithm (by the mass reconstruction) improves the sensitivity.

Table 1 The \(95\%\) CL upper limits on the signal strengths (\(\mu _\phi \)) and the production cross sections for \(m_{\phi }=95,\,100,\,105\,\text {GeV}\) are summarized. These limits are obtained from the ATLAS Run 2 full data [55] in the boosted \(\tau \bar{\tau }\) (boost_2 category) and \(t\bar{t} +\tau \bar{\tau }\) (\(tt(0\ell ) + \tau _\textrm{h} \tau _\textrm{h}\) category) searches, via the \(\chi ^2\) test defined in Eq. (27)
Full size table

Since experimental analyses have used the boosted decision tree (BDT) techniques, it is difficult to access the detailed information about the final kinematic cuts. Instead, we utilize the data in ttH_1 category, corresponding to the right panel of Fig. 11 of Ref. [55], where the \(t\bar{t}h\) events are optimised to be enhanced over Z and \(t\bar{t}\) Bkg events by the BDT. In the plot, \((\text {data yields)}-(\text {SM Bkg except for the SM Higgs})\) is shown (\(N_\textrm{ob} \pm \Delta N_\textrm{ob}\)), as well as uncertainty of the total SM Bkg (\(\pm \Delta N_\textrm{Bkg}\)) and the SM Higgs histogram (\(N_{h}\)). From this figure, we estimate the sensitivity to probe the new resonance, supposing that the \(m_{\tau \tau }\) distribution of \(t\bar{t} +\phi \rightarrow t\bar{t} + \tau \bar{\tau }\) under the BDT is similar to the SM Higgs.

Similar to the previous section, we define a signal strength for the top-associated production of \(\phi \),

$$\begin{aligned} \mu _\phi (t\bar{t}+\tau {\bar{\tau }}) \equiv \frac{\sigma (pp\rightarrow t\bar{t}+\phi )\times \textrm{BR}(\phi \rightarrow \tau {\bar{\tau }})}{\sigma (pp\rightarrow t\bar{t}+h)_\mathrm{{SM}}\times \textrm{BR}(h\rightarrow \tau {\bar{\tau }})_\mathrm{{SM}}}. \end{aligned}$$
(26)

In the right panel of Fig. 2, an expected histogram of \(\phi \) with \(m_{\phi }=95\,\text {GeV}\) and \(\mu _{\phi }(t\bar{t}+\tau {\bar{\tau }}) =2\) is shown by the blue shaded region. Since the each bin width in the data is \(10\,\text {GeV}\), we simply shift the distribution of the SM Higgs histogram by three bins to obtain the distribution of \(m_\phi =95\,\text {GeV}\).Footnote 8 Since the width of the SM Higgs histogram stems from the experimental resolution, it is expected that the width of the histogram of \(\phi \) is roughly of the same size as the SM Higgs. Moreover, if the resolution is proportional to the value of \(m_{\tau \tau }\), the histogram of \(\phi \) becomes sharpened. Therefore, we just rescale the SM Higgs histogram to conservatively predict the \(\phi \) contribution. We represent the histogram of \(\phi \) by \(N_\phi (\mu _\phi )\). Again, the SM Higgs histogram (red shaded region) is scaled by 1/0.93 from the original one.

We perform the following \(\chi ^2\) test,

$$\begin{aligned} \chi ^2 (\mu _\phi )&= \text {max} \left[ \chi ^2_i(\mu _\phi ) \right] \quad \text {and} \quad \chi ^2_i(\mu _\phi )\nonumber \\&=\sum _{j=i}^{i+2} \frac{\left[ N_\textrm{ob}^j -N_{h}^{j} - N_{\phi }(\mu _\phi )^j \right] ^2}{(\Delta N_\textrm{ob}^{j})^2+(\Delta N_\textrm{Bkg}^j)^2} , \end{aligned}$$
(27)

where i and j are indices of each bin. Note that since correlations between the data in each bin are not available in Ref. [55], we discard them for simplicity. Due to the finite experimental resolution for the \(m_{\tau \tau }\) distribution, judging based on the single bin data is too aggressive. Here, we use at least 3 contiguous bins for each \(\chi ^2_i(\mu _\phi )\) evaluation.Footnote 9 The criterion for setting the upper limit on \(\mu _\phi \) is \(\chi ^2(\mu _\phi ) < \chi ^2_{3\text {dof}, 95\%} \simeq 7.82\).

As a validation of this \(\chi ^2\) test, we compare the upper limit on the SM Higgs production cross section in the ttH_1 category. We obtain the 95% CL upper limit for the Higgs boson cross section,

$$\begin{aligned} \mu _h = \frac{\sigma (pp\rightarrow t\bar{t}+h) \times \textrm{BR}(h \rightarrow \tau \bar{\tau })}{\sigma (pp\rightarrow t\bar{t}+h)_\textrm{SM} \times \textrm{BR}( h \rightarrow \tau \bar{\tau })_\textrm{SM}}\le 2.65, \end{aligned}$$
(28)

while \(\mu _h \lesssim 2.96\) (\(\mu _h=1.02^{+0.97}_{-0.81}\)) has been set in Ref. [55]. It is found that the \(\chi ^2\) test in Eq. (27) gives a slightly severe limit. This could be attributed to the following reasons; This \(\chi ^2\) test does not include the theoretical uncertainty of the signal events properly. The total uncertainty (dashed band \(\Delta N_\textrm{Bkg}\)) includes the theoretical uncertainty of \(\mu _h \simeq 1\) and it should be inflated according as \(\mu _h\). Second, when we evaluate the \(\chi ^2_i\) value for at least not 3 but 4 contiguous bins, the resultant limit is weakened by 5–\(10\%\). Therefore, we decide to weaken the obtained upper limit on \(\mu _{\phi }\) by \(10\%\) to be conservative test. In this prescription, we obtain \(\mu _h < 2.92\).

Using the \(\chi ^2\) test, we set the \(95\%\) CL upper limit on the signal strength,

$$\begin{aligned} \mu _\phi (t\bar{t}+\tau \bar{\tau }) < 1.56 \quad \text {for }m_{\phi } = 95\,\text {GeV}, \end{aligned}$$
(29)

or equivalently,

$$\begin{aligned} \sigma (pp \rightarrow t\bar{t} + \phi )\times \textrm{BR}(\phi \rightarrow \tau {\bar{\tau }})&< 0.050 \,\textrm{pb}\quad \nonumber \\ \text {for }m_{\phi }&= 95\,\text {GeV}. \end{aligned}$$
(30)

It is found that the CP-even scalar H interpretation on the CMS di-tau is excluded by the ATLAS \(t\bar{t}+\tau \bar{\tau }\) search, while the CP-odd A one is consistent with the ATLAS (see Eqs. (11) and (19)). Note that due to the fixed bin width, we can not perform the same analysis for the \(m_\phi =100\,\text {GeV}\) case.Footnote 10 Our results are summarized in Table 1.

Fig. 3
figure 3

The obtained ATLAS \(95\%\) CL limits are shown on a \(\rho _{\tau \tau }\)–\(\rho _{tt}\) plane (see Table 1). The gray shaded regions surrounded by the solid and dashed lines are excluded by the ATLAS boosted \(\tau \bar{\tau }\) and \(t\bar{t}+\tau \bar{\tau }\) searches, respectively. The left panel is for the CP-even (H) case and the right one is for the CP-odd (A). The CMS di-tau and di-photon excesses can be explained at the \(1\sigma \) level in the yellow and blue regions, respectively. The global fits at the \(1\sigma \) (\(2\sigma \)) level are shown by the purple solid (dashed) circles. The scalar boson mass is set to be \(95\,\text {GeV}\)

Full size image

Finally, we project the obtained ATLAS limits onto the the minimal setup in Eq. (4). In Fig. 3, we show the ATLAS limits from the data in the boosted \(\tau {\bar{\tau }}\) and \(t\bar{t}+\tau {\bar{\tau }}\) searches by the gray shaded regions surrounded by the solid and dashed lines, respectively. The CP-even (odd) scalar with \(m_{H(A)}=95\,\text {GeV}\) is considered in the left (right) panel. The CMS di-tau excess in Eq. (1) can be explained in the yellow region. For the branching ratio, we calculate \(H(A) \rightarrow \tau \bar{\tau }\) at the tree level and \(gg,\,\gamma \gamma \) and \(Z\gamma \) at the one-loop level [56] for the decay channels. Furthermore, the aforementioned CMS di-photon excess can be explained in the blue region corresponding to [13, 23]

$$\begin{aligned} \sigma (gg \rightarrow \phi )\times \textrm{BR}(\phi \rightarrow \gamma \gamma ) = 0.058\pm 0.019\,\textrm{pb}, \end{aligned}$$
(31)

where the SusHi and Ref. [57] are used for the \(95\,\text {GeV}\) SM-like Higgs value. It is clearly shown that an interesting parameter region that can explain both di-tau and di-photon excesses is almost excluded in the CP-even scalar case. Note that although the results on Fig. 3 assume the minimal setup in Eq. (4), the statement that the anomaly-driven parameter region is excluded in the CP-even scalar case is independent of the effective Lagrangian as long as the gluon-fusion is dominated in the top-quark contribution. Additional interactions including dark sectors reduce only \(\text {BR}(\phi \rightarrow \tau {\bar{\tau }})\). This effect shifts the results to the upper-right direction on Fig. 3, but the relative positions do not change.

3.3 Comment on \(t\bar{t}+\gamma \gamma \) search

Motivated by the CMS di-photon excess in Eq. (31), we point out that the above procedure can be repeated to estimate the upper limit on \(\sigma (pp \rightarrow t\bar{t}+\phi )\times \textrm{BR}(\phi \rightarrow \gamma \gamma )\) by analysing \(pp \rightarrow t\bar{t} + h \rightarrow t\bar{t} + \gamma \gamma \) process. This process must be cleaner than the \(pp\rightarrow t\bar{t} + \{h,Z\} \rightarrow t\bar{t}+\tau \bar{\tau }\). This is because the \(Z \rightarrow \gamma \gamma \) decay is forbidden (the Landau–Yang theorem [58, 59]) so much smaller SM Bkg is expected around \(m_{\gamma \gamma } \sim 90\,\text {GeV}\).Footnote 11 Furthermore, \(\sigma (pp \rightarrow t\bar{t}+\phi )\times \textrm{BR}(\phi \rightarrow \gamma \gamma )\) is expected to be the same size as the \(\sigma (pp \rightarrow t\bar{t}+h)_\textrm{SM}\times \textrm{BR}(h \rightarrow \gamma \gamma )_\textrm{SM}\). Therefore, the search for the additional resonance in \(pp \rightarrow t\bar{t} + \gamma \gamma \) is promising.

Indeed, such a check has been implicitly done in the CMS collaboration [13]. However, we could not find any results of direct searches for \(pp \rightarrow t \bar{t} + \gamma \gamma \) in a region of \(m_{\gamma \gamma }\le 105\,\text {GeV}\) [49, 60, 61] (see, e.g., Fig. 2 of Ref. [60]). Therefore, we would like to suggest an experimental analysis of the \(pp \rightarrow t \bar{t} + \gamma \gamma \) process with the low-mass region to probe the additional resonance.

4 Summary and discussion

Due to the nature of the high-energy proton collider and its harsh hadron activity, it is difficult to probe weakly interacting colorless new particles below \({\mathcal {O}}(100)\,\text {GeV}\) mass region. Very recently, the CMS collaboration has reported a di-tau excess with a local significance of 2.6–3.1\(\sigma \) around \(m_{\tau \tau }=95\)–\(100\,\text {GeV}\). This excess can be interpreted as an additional scalar boson \(\phi \) produced via the gluon-fusion process. Interestingly, in the same mass region, two other excesses have been reported; a di-photon excess by the CMS collaboration and an excess in \(e^+e^- \rightarrow Z b\bar{b}\) from the LEP experiment.

In this paper, we focus on the CMS di-tau excess. This excess can be explained by the light scalar \(\phi \) which couples with the top and \(\tau \) in the minimal setup. First, we found that the minimal scalar model is still consistent with the ATLAS result for the similar boosted \(\tau \bar{\tau }\) search, where a huge SM Bkg comes from the Z-boson DY production. Second, we point out that the minimal scalar model predicts the inevitable correlation with the top-quark associated process (\(gg \rightarrow t\bar{t} +\tau {\bar{\tau }}\)), see the Feynman diagrams in Fig. 1. Moreover, a requirement of an additional top-quark pair in the final state suppresses the huge Z-boson DY Bkg, so that the experimental sensitivity to probe \(\phi \) is certainly better compared to the boosted \(\tau \bar{\tau }\) search around \(m_{\tau \tau }=95\)–\(100\,\text {GeV}\), although the statistics are limited.

Based on the ATLAS data available in Ref. [55], we obtain the \(95\%\) CL upper limits on the gluon-fusion and top-associated production cross sections in the minimal setup, which are summarized in Table 1. One of important points is that the limits depend on the CP eigenstate of \(\phi \), i.e., whether \(\phi \) is CP-even (H) or CP-odd (A). We point out that the gluon-fusion production cross section is twice larger in the A case, while the top-associated production cross section is three times larger in the H case including the QCD higher-order corrections. This difference is caused by the \(\gamma _5\) structure in the Yukawa interaction. As the result, it is found that the H interpretation on the di-tau excess is excluded by the ATLAS \(t\bar{t}+\tau \bar{\tau }\) search, while the A case is allowed, see Fig. 3. The available ATLAS data (the \(tt(0\ell ) + \tau _\textrm{h} \tau _\textrm{h}\) category) is pure hadronic final states. We also hope the ATLAS collaboration to stop categorizing and to combine both leptonic [62, 63] and hadronic decay modes [55] to increase the sensitivity to probe a possible new particle. The similar analysis could also be applied in \(t\bar{t}+\gamma \gamma \) search to probe a possible light resonance that can accommodate the CMS di-photon excess.

Note that the LEP \(b\bar{b}\) excess implies that \(\phi \) is the CP-even state (H) because the Z-boson-associated A production vanishes. Therefore, once the \(b\bar{b}\) excess is involved seriously, the CP symmetry must be violated in the scalar model. Such CP-violating parameters (Yukawa or scalar self interactions) would induce the electron electric dipole moment at two-loop level (e.g., Ref. [64]). Furthermore, a search for \(t\bar{t}+b\bar{b}\) signature would be interesting in light of the \(b\bar{b}\) excess. Although Fig. 12 of Ref. [65] would be helpful to check the \(b\bar{b}\) excess, the measurement suffers from the QCD jets. The more statistics and dedicated study are necessary to make a clear conclusion.

An additional vector particle (\(A'\)) would be also a possibility for the CMS di-tau excess. The simplest possibility is the hidden-photon model [66, 67]. The production of \(A'\) is the DY process and the decay branching ratio is fixed [\(\textrm{BR}(A'\rightarrow \tau \bar{\tau })\simeq 15\%\)] [68]. Currently there is no direct experimental bound on the \(A'\) production with mass region of around 90 GeV at the LHC [69]. Instead, an indirect bound comes from measurements of the EW precision observables at the LEP and Tevatron experiments [70]. It is, however, beyond the scope of this paper to examine whether the \(A'\) interpretation is allowed.

We also comment on our prescription for the \(\chi ^2\) test in Eq. (27). Our prescription is intuitive and does not rely on realistic Monte-Carlo simulations. Necessary cut information for the detailed analysis is not available from the experimental papers because the BDT algorithm is adopted. Our prescription may receive additional effects from the BDT, since the BDT variables include the sub-leading \(p_\textrm{T}^\tau \) and missing transverse momentum.

Since the current ATLAS data is consistent with the CMS di-tau excess if a light CP-odd scalar is introduced, it is nice to consider specific new physics models. A light CP-odd scalar emerges as a pseudo-Nambu–Goldstone (NG) boson which comes from the spontaneous symmetry breaking of some global symmetries. Such a mass of the pseudo-NG boson does not lead to an additional fine-tuning problem.

Within the G2HDM, additional scalars appear in the same mass scale with moderate mass differences of \({\mathcal {O}}\)(VEV) (see, Ref. [71] for instance). It is possible to predict the lighter CP-odd scalar in general. Nevertheless the mass degenerated setup, where only \(\rho _{tt}\) and \(\rho _{\tau \tau }\) are assumed to be nonzero, is not compatible with the direct search for the charged scalar in \(pp\rightarrow tb + H^\pm \rightarrow tb+\tau \nu ~\mathrm{{or}}~tb\) [43, 44]. Therefore the heavier charged scalar is necessary while keeping the CP-odd scalar mass to be around 95\(\,\text {GeV}\).Footnote 12 Another possible solution to this dilemma is to put the additional coupling and open up a new decay mode of a charged scalar. However, additional Yukawa couplings could also contribute to the scalar production and suffers from the direct searches. The weakest constrained Yukawa coupling is a top-charm flavor violating coupling, \(\rho _{tc}\), where top quark is a left handed and charm quark is right handed. Since the top mass is heavier than 100 GeV, the coupling does not reduce the BR(\(\phi \rightarrow \tau \bar{\tau }\)). On the other hand the \(SU(2)_L\) rotation generates \(H^-\rightarrow b\bar{c}\) decay when \(\rho _{tc}\) is not vanishing. It is recently pointed out that low-mass di-bottom jets would be sensitive to this coupling depending on the mass [72]. It is worthwhile to comment that the non-zero product of \(\rho _{tc}\) and \(\rho _{\tau \tau }\) can enhance \(R_{D^{(*)}}=\mathrm{{BR}}(\bar{B}\rightarrow D^{(*)} \tau \bar{\nu })/\mathrm{{BR}}(\bar{B}\rightarrow D^{(*)} \ell \bar{\nu }\)), where \(\ell =e,\,\mu \) and the 3–4\(\sigma \) discrepancy is reported [73, 74], consistently with the \(B_c\)-meson lifetime [75].Footnote 13 The non-zero \(\rho _{tc}\) with the large mass difference between neutral scalars induces the same sign top signal [77]. This is also interesting as well as the search for a light scalar in the double-scalar production at the LHC [78]. The more quantitative and dedicated study is beyond this paper and will be given elsewhere.