Fluctuations of non-ergodic stochastic processes

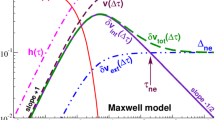
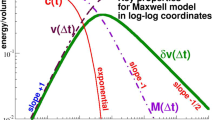
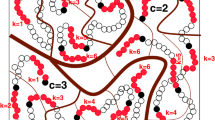
Abstract

We investigate the standard deviation $\delta v(\Delta t)$ of the variance $v[\mathbf {x}]$ of time series $\mathbf {x}$ measured over a finite sampling time $\Delta t$ focusing on non-ergodic systems where independent “configurations” c get trapped in meta-basins of a generalized phase space. It is thus relevant in which order averages over the configurations c and over time series k of a configuration c are performed. Three variances of $v[\mathbf {x}_{ck}]$ must be distinguished: the total variance $\delta v^2_{\mathrm {tot}}= \delta v^2_{\mathrm {int}}+ \delta v^2_{\mathrm {ext}}$ and its contributions $\delta v^2_{\mathrm {int}}$, the typical internal variance within the meta-basins, and $\delta v^2_{\mathrm {ext}}$, characterizing the dispersion between the different basins. We discuss simplifications for physical systems where the stochastic variable x(t) is due to a density field averaged over a large system volume V. The relations are illustrated for the shear-stress fluctuations in quenched elastic networks and low-temperature glasses formed by polydisperse particles and free-standing polymer films. The different statistics of $\delta v_{\mathrm {int}}$ and $\delta v_{\mathrm {ext}}$ are manifested by their different system-size dependences.

Graphic abstract

Appendices

A System-size exponents $\gamma _{\mathrm {int}}$ and $\gamma _{\mathrm {ext}}$

We focus here on properties obtained for $\Delta t\gg \tau _{\mathrm {b}}$. The time dependence becomes thus irrelevant. Due to the non-ergodicity the c-dependence remains relevant, however, and we compute k-averages $\mathbf {E}^{k}\ldots = \left\langle \ldots \right\rangle _c$ over all stochastic variables $x = \mathbf {E}^m x_m$ being themselves averages over $n_\mathrm {m}$ microscopic variables $x_m$ and compatible with the non-ergodicity constraint of the configuration c considered. Our task is to compute

$$\begin{aligned} v = \mathbf {E}^c v_c \text{ and } \Delta _{\mathrm {ne}}^2 = \mathbf {V}^cv_c \text{ for } v_c \equiv \left\langle x^2 \right\rangle _c - \left\langle x \right\rangle _c^2. \end{aligned}$$

(59)

We assume that the microscopic variables $x_m$ are decorrelated as they come from uncorrelated microcells and set $v_{cm} \equiv \left\langle x_m^2 \right\rangle _c - \left\langle x_m \right\rangle _c^2$ for the variance of the microscopic variable $x_m$. Using the independence of the microcells m yields

$$\begin{aligned} v_c= & {} \frac{1}{n_\mathrm {m}} \times \left( \frac{1}{n_\mathrm {m}} \sum _m v_{cm} \right) \end{aligned}$$

(60)

$$\begin{aligned} \mathbf {V}^cv_c= & {} \frac{1}{n_\mathrm {m}^3} \times \left( \frac{1}{n_\mathrm {m}} \sum _m \mathbf {V}^cv_{cm} \right) \end{aligned}$$

(61)

where we have used that also the variances $v_{cm}$ are independent stochastic variables. Note that the $m-$averages (brackets) do not depend on $n_\mathrm {m}$ for large $n_\mathrm {m}$. Hence,

$$\begin{aligned} v = \mathbf {E}^c v_c \propto 1/n_\mathrm {m} \text{ and } \Delta _{\mathrm {ne}}\propto 1/n_\mathrm {m}^{3/2}. \end{aligned}$$

(62)

We have thus confirmed the exponents $\hat{\gamma }_{\mathrm {int}}\equiv \gamma _{\mathrm {int}}+1=1$ and $\hat{\gamma }_{\mathrm {ext}}\equiv \gamma _{\mathrm {ext}}+ 1=3/2$ stated in Sect. 2.4 for uncorrelated microscopic variables.

B Distribution of $v_c$

Since $\delta v^2_{\mathrm {ext}}= \mathbf {V}^c v_c$ is finite, the $v_c = \mathbf {E}^k v[\mathbf {x}_{ck}]$ of different configurations c must differ. It is useful to rewrite Eq. (20) by setting $v_c = v (1+\delta _c)$ in terms of the “dimensionless dispersion” $\delta _c$. Using $\mathbf {E}^c \delta _c = 0$ we have

$$\begin{aligned} (\delta v_{\mathrm {ext}}/v)^{2} \equiv s^2 = \ \mathbf {E}^c \delta _c^2 = \int \mathrm {d}\delta _c \ p(\delta _c) \ \delta _c^2 \end{aligned}$$

(63)

with s being the standard deviation of the normalized distribution $p(\delta _c)$. For a Gaussian distribution all moments are set by s. In general, however, $p(\delta _c)$ may be non-Gaussian and may depend on the preparation history. It may even happen in principle that some higher moments do not exist. We present in Fig. 10 the normalized distribution p(x) for the rescaled dispersion $x = \delta _c/s$. A broad range of cases is considered. The histograms are obtained using the $n_\mathrm {c}= 100$ independent configurations. A reasonable data collapse on the Gaussian distribution (bold solid line) is observed. This indicates that $\delta v_{\mathrm {ext}}$ or s are sufficient for the characterization of the distribution of the dispersion $\delta _c$. The Gaussianity was also checked by means of the standard non-Gaussianity parameter [7], comparing the forth and the second moment of the distribution. Clearly, an even larger number $n_\mathrm {c}$ is warranted in future work for a more critical test of the tails of the distribution using a half-logarithmic representation.

Fig. 10

Normalized histogram p(x) for different $\Delta t$ and $n_\mathrm {k}$ as indicated. The histograms are well described by a Gaussian (bold solid line)