Simple models for strictly non-ergodic stochastic processes of macroscopic systems

Abstract

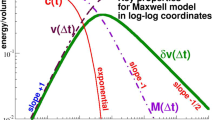
We investigate simple models for strictly non-ergodic stochastic processes $x_t$ (t being the discrete time step) focusing on the expectation value v and the standard deviation $\delta v$ of the empirical variance $v[\mathbf {x}]$ of finite time series $\mathbf {x}$. $x_t$ is averaged over a fluctuating field $\sigma _{\mathbf{r}}$ ($\mathbf{r}$ being the microcell position) characterized by a quenched spatially correlated Gaussian field $g_{\mathbf{r}}$. Due to the quenched $g_{\mathbf{r}}$-field $\delta v(\varDelta \tau )$ becomes a finite constant, $\varDelta _{\mathrm {ne}}> 0$, for large sampling times $\varDelta \tau$. The volume dependence of the non-ergodicity parameter $\varDelta _{\mathrm {ne}}$ is investigated for different spatial correlations. Models with marginally long-ranged $g_{\mathbf{r}}$-correlations are successfully mapped on shear stress data from simulated amorphous glasses of polydisperse beads.

Appendices

Correlation functions of Gaussian fields

Let $y_i$ be a normal distributed random field of zero mean, i.e., $\langle y_i \rangle = \mu _1 = 0$, with i standing for the discrete time or spatial position. ($\langle \ldots \rangle$ stands here for a c-average over $n_\mathrm {c}\rightarrow \infty$ independent configurations.) Wick’s theorem [1] thus holds, i.e.,

$$\begin{aligned} \left<y_i y_j y_k y_l \right>= \left<y_i y_j \right>\left<y_k y_l \right>+ \left<y_i y_k \right>\left<y_j y_l \right>+ \left<y_i y_l \right>\left<y_j y_k \right>.\nonumber \\ \end{aligned}$$

(44)

This implies in turn $\langle y_i^2 y_j^2 \rangle - \langle y_i^2 \rangle \langle y_j^2 \rangle = 2 \langle y_i y_j \rangle ^2$. With the indices corresponding to spatial positions and assuming translational invariance, this shows that $C_2(\mathbf{r}) = 2 C_1(\mathbf{r})^2$ for $\mu _1 = 0$. If we consider instead the field $g_i = y_i + \mu _1$ with finite first moment $\mu _1 = \langle g_i \rangle$, $C_1(\mathbf{r})$ remains unchanged, while $C_2(\mathbf{r})$ does not. By substituting $y_i=g_i-\mu _1$, expanding $C_2(\mathbf{r})$ and using the invariance of $C_1(\mathbf{r})$, it is seen that more generally Eq. (37) holds.⁹

Random Gaussian fields $g_{\mathbf{r}}$ corresponding to the models of Sect. 4.2 have been explicitly generated numerically and we have measured the correlation functions $C_l(\mathbf{r}=\mathbf{r}''-\mathbf{r}')$ by averaging (consistently with the periodic boundary conditions) over all pairs of cells $\mathbf{r}'$ and $\mathbf{r}''$ and the $n_\mathrm {c}$ independent configurations. Model A is trivially obtained by generating for each configuration $n_{\mathbf{r}}$ uncorrelated normal-distributed random numbers $\zeta _{\mathbf{r}}$ of zero mean and unit variance and setting $g_{\mathbf{r}}= \mu _1 + a_0 \zeta _{\mathbf{r}}$ with $c_1 = a_0^2$. Spatially correlated random numbers $y_{\mathbf{r}}=g_{\mathbf{r}}-\mu _1$ are obtained by setting $y_{\mathbf{r}'} = \sum _{\mathbf{r}''} a_{\mathbf{r}'\mathbf{r}''} \zeta _{\mathbf{r}'}$ where the “response” matrix $a_{\mathbf{r}'\mathbf{r}''}$ is uniquely determined by the imposed correlation function $C_1(\mathbf{r})$ as shown below. Importantly, $g_{\mathbf{r}}=y_{\mathbf{r}}+\mu _1$ is thus a linear superposition of Gaussian variables and therefore also Gaussian.¹⁰ As a consequence, Eq. (37) applies. Following a standard procedure [19], one way to obtain the $y_{\mathbf{r}}$-fields is to compute in turn the Fourier transforms $\zeta _{\mathbf{q}} = \mathcal{F}[\zeta _{\mathbf{r}}]$ and $C_1(\mathbf{q}) = \mathcal{F}[C_1(\mathbf{r})]$, the product $y_{\mathbf{q}} = \sqrt{C_1(\mathbf{q})} \zeta _{\mathbf{q}}$, and finally the inverse Fourier transform $y_{\mathbf{r}} = \mathcal{F}^{-1}[y_{\mathbf{q}}]$ with $\mathcal{F}$ standing for the d-dimensional discrete Fourier transform and $\mathcal{F}^{-1}$ for its inverse. It is used here that $\zeta _{\mathbf{q}} \zeta _{-\mathbf{q}} = 1$ and that $C_1(\mathbf{q})$ is real, even, positive and commensurate with the simulation box.

Fig. 8

$C_1(\mathbf{r})$ and $C_2(\mathbf{r})$ for model C with $\alpha _1=1/2$, $\mu _1=0$, $\mu _2=c_1=1$ and $\xi =1$. The open symbols have been obtained for $d=1$ and $L=1000$, the filled symbols for $d=2$ and $L=200$. Main: Double-logarithmic representation for logarithmically binned data. As emphasized by the solid line $\alpha _2=2\alpha _1=1$. Inset: Linear representation for small r

That the procedure works can be seen in Fig. 8 for model C in $d=1$ and $d=2$ (filled symbols). We have set $\alpha _1 = 1/2$, $\mu _1=0$ and $\mu _2=c_1=1$. The data for $C_1(\mathbf{r})$ and $C_2(\mathbf{r})$ are obtained by averaging over $n_\mathrm {c}=10^4$ independent configurations. Due to Eq. (37), we have $C_2(\mathbf{r}) \simeq c_2/r^{\alpha _2}$ with $\alpha _2 = 2 \alpha _1 =1$ as shown by the solid line in the main panel. The spatial dimension only plays a role for small and finite $r \approx 1$ as may be seen from the inset of Fig. 8. This leads to a weak d-dependence of integrals dominated by the lower integration bound.

Alternative quenched field

An interesting alternative quenched field is given by the “local covariance” $v_{c\mathbf{r}} \equiv V \mathbf {E}^k \delta \sigma _{ck\mathbf{r}} \delta \sigma _{ck}$ between the local and total fluctuations $\delta \sigma _{ck\mathbf{r}}$ and $\delta \sigma _{ck} = \mathbf {E}^{\mathbf{r}} \delta \sigma _{ck\mathbf{r}}$. Note that $v_c = \mathbf {E}^{\mathbf{r}} v_{c\mathbf{r}}$ holds since $\mathbf {E}^k$ and $\mathbf {E}^{\mathbf{r}}$ commute. Importantly, for many physical systems $v_{c\mathbf{r}}$ corresponds to a local modulus, e.g., the local stress-fluctuation contribution to an elastic modulus [15]. Using $\delta v_{c\mathbf{r}} = v_{c\mathbf{r}} -v$, we may write quite generally without any additional assumption

$$\begin{aligned} \varDelta _{\mathrm {ne}}^2= \mathbf {E}^{\mathbf{r}'} \mathbf {E}^{\mathbf{r}''} \underline{\mathbf {E}^{c} \delta v_{c\mathbf{r}'} \delta v_{c\mathbf{r}''}} = \mathbf {E}^{\mathbf{r}} C[v_{\mathbf{r}}](\mathbf{r}) \end{aligned}$$

(45)

where $C[v_{\mathbf{r}}](\mathbf{r})$ stands for the average of the underlined term over all pairs of microcells $\mathbf{r}'$ and $\mathbf{r}''=\mathbf{r}'+\mathbf{r}$.¹¹ As a consequence, a slow V-decrease of $\varDelta _{\mathrm {ne}}$ with $\gamma _{\mathrm {ext}}< 1/2$ must arise if $C[v_{\mathbf{r}}](\mathbf{r})$ is long-ranged. One may model the field $v_{\mathbf{r}}$ by means of a spatially correlated variable $g_{\mathbf{r}}$, i.e., using the notations of Sect. 4.1, we have $v = \mu _1$, $\varDelta _{\mathrm {ne}}= \varDelta _1$ and the correlation function $C_1(\mathbf{r})$ corresponds to $C[v_{\mathbf{r}}](\mathbf{r})$. This yields a good alternative fit of the shear stress data discussed in Sect. 5 using model D with $\alpha _1=2$, $\mu _1=v=17.1$, $\mu _2=293$ and $\xi =3.3$. To discriminate between both modeling approaches, a numerical comparison of correlation functions of different k-averaged quenched fields is warranted [17].