An inventory model for deteriorating items with time-dependent demand and time-varying holding cost under partial backlogging

Abstract

In this paper, we considered a deterministic inventory model with time-dependent demand and time-varying holding cost where deterioration is time proportional. The model considered here allows for shortages, and the demand is partially backlogged. The model is solved analytically by minimizing the total inventory cost. The result is illustrated with numerical example for the model. The model can be applied to optimize the total inventory cost for the business enterprises where both the holding cost and deterioration rate are time dependent.

Background

In the traditional inventory models, one of the assumptions was that the items preserved their physical characteristics while they were kept stored in the inventory. This assumption is evidently true for most items, but not for all. However, the deteriorating items are subject to a continuous loss in their masses or utility throughout their lifetime due to decay, damage, spoilage, and penalty of other reasons. Owing to this fact, controlling and maintaining the inventory of deteriorating items becomes a challenging problem for decision makers.

Harris ([1915]) developed the first inventory model, Economic Order Quantity, which was generalized by Wilson ([1934]) who gave a formula to obtain economic order quantity. Whitin ([1957]) considered the deterioration of the fashion goods at the end of the prescribed shortage period. Ghare and Schrader ([1963]) developed a model for an exponentially decaying inventory. Dave and Patel ([1981]) were the first to study a deteriorating inventory with linear increasing demand when shortages are not allowed. Some of the recent work in this field has been done by Chung and Ting ([1993]); Wee ([1995]) studied an inventory model with deteriorating items. Chang and Dye ([1999]) developed an inventory model with time-varying demand and partial backlogging. Goyal and Giri ([2001]) gave recent trends of modeling in deteriorating item inventory. They classified inventory models on the basis of demand variations and various other conditions or constraints. Ouyang and Cheng ([2005]) developed an inventory model for deteriorating items with exponential declining demand and partial backlogging. Alamri and Balkhi ([2007]) studied the effects of learning and forgetting on the optimal production lot size for deteriorating items with time-varying demand and deterioration rates. Dye et al. ([2007]) find an optimal selling price and lot size with a varying rate of deterioration and exponential partial backlogging. They assume that a fraction of customers who backlog their orders increases exponentially as the waiting time for the next replenishment decreases.

In 2008, Roy developed a deterministic inventory model when the deterioration rate is time proportional. Demand rate is a function of selling price, and holding cost is time dependent. Liao ([2008]) gave an economic order quantity (EOQ) model with non instantaneous receipt and exponential deteriorating item under two level trade credits

Pareek et al. ([2009]) developed a deterministic inventory model for deteriorating items with salvage value and shortages. Skouri et al. ([2009]) developed an inventory model with ramp-type demand rate, partial backlogging, and Weibull's deterioration rate. Mishra and Singh ([2010]) developed a deteriorating inventory model for waiting time partial backlogging when demand and deterioration rate is constant. They made the work of Abad ([1996][, 2001]) more realistic and applicable in practice.

Mandal ([2010]) gave an EOQ inventory model for Weibull-distributed deteriorating items under ramp-type demand and shortages. Mishra and Singh ([2011a], [b]) gave an inventory model for ramp-type demand, time-dependent deteriorating items with salvage value and shortages and deteriorating inventory model for time-dependent demand and holding cost with partial backlogging. Hung ([2011]) gave an inventory model with generalized-type demand, deterioration, and backorder rates.

In classical inventory models, the demand rate and holding cost is assumed to be constant. In reality, the demand and holding cost for physical goods may be time dependent. Time also plays an important role in the inventory system; therefore, in this inventory system, we consider that demand and holding cost are time dependent.

In this paper, we made the work of Roy ([2008]) more realistic by considering demand rate and holding cost as linear functions of time and developed an inventory model for deteriorating items where deterioration rate is expressed as a linearly increasing function of time. Shortages are allowed and partially backlogged. The assumptions and notations of the model are introduced in the next section. The mathematical model and solution procedure are derived in the ‘Mathematical formulation and solution’ section, and the numerical and graphical analysis is presented in the ‘Results and discussion’ section. The article ends with some concluding remarks and scope of future research.

Methods

Assumption and notations

This inventory model is developed on the basis of the following assumption and notations:

• i. Deterioration rate is time proportional.

• ii. θ(t) = θt, where θ is the rate of deterioration; 0 < θ < 1.

• iii. Demand rate is time dependent and linear, i.e., D(t) = a + bt; a, b > 0 and are constant.

• iv. Shortage is allowed and partially backlogged.

• v. C ₂ is the shortage cost per unit per unit time.

• vi. β is the backlogging rate; 0 ≤ β ≤ 1.

• vii. During time t ₁, the inventory is depleted due to the deterioration and demand of item. At time t ₁, the inventory becomes zero and shortage starts occurring.

• viii. There is no repair or replenishment of deteriorating item during the period under consideration.

• ix. Replenishment is instantaneous; lead time is zero.

• x. T is the length of the cycle.

• xi. The order quantity of 1 cycle is q.

• xii. Holding cost h(t) per unit time is time dependent and is assumed h(t) = h + αt, where α > 0; h > 0.

• xiii. C is the unit cost of an item.

• xiv. IB is the maximum inventory level during the shortage period.

• xv. I ₀ is the maximum inventory level during (0, T).

• xvi. S is the lost sale cost per unit.

Mathematical formulation and solution

The rate of change of the inventory during the positive stock period (0, t₁) and shortage period (t₁, T) is governed by the following differential equations:

$$\frac{d{I}_1\left(t\right)}{\mathit{dt}}=-D\left(t\right)-\theta \left(t\right)I_1\left(t\right),0\le t\le t_1,$$

(1)

$$\frac{d{I}_2\left(t\right)}{\mathit{dt}}=-\mathit{\beta D}\left(t\right),t_1\le t\le T.$$

(2)

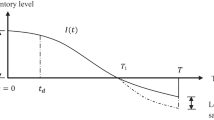
The initial inventory level is I₀ unit at time t = 0; from t = 0 to t = t₁, the inventory level reduces, owing to both demand and deterioration, until it reaches zero level at time t = t₁. At this time, shortage is accumulated which is partially backlogged at the rate β. At the end of the cycle, the inventory reaches a maximum shortage level so as to clear the backlogged and again raises the inventory level to I₀ (Figure 1).

Figure 1

Graphical representation of the state of inventory system.

Thus, boundary conditions are as follows:

$$I_1\left(0\right)=I_0,I_1\left(t_1\right)=0,I_2\left(t_1\right)=0.$$

The solutions of Equations 1 and 2 with boundary conditions are as follows:

$$\begin{array}{l}{\mathit{I}}_1\left(\mathit{t}\right)\mathit{=}\mathit{-}{\mathit{e}}^{-\frac{\theta t^2}{2}}{\displaystyle {\int }_{\mathit{t}}^{{\mathit{t}}_1}{\mathit{e}}^{\frac{\theta t^2}{2}}}\left(\mathit{a}+\mathit{bt}\right)\mathit{dt}\\ 0\le \mathit{t}\le {\mathit{t}}_1,\end{array}$$

(3)

$$\begin{array}{l}{I}_2\left(t\right)=-\beta \left[a\left(T-t\right)+\frac{b}{2}\left(T^2-t_1^2\right)\right]\\ t_1\le t\le \mathit{T}.\end{array}$$

(4)

Using Equation 3, we get the following:

$${\mathit{I}}_0={\displaystyle {\int }_0^{{\mathit{t}}_1}\left(\mathit{a}+\mathit{bt}\right){\mathit{e}}^{\frac{\theta t^2}{2}}}\mathit{dt}.$$

(5)

Inventory is available in the system during the time interval (0, t₁). Hence, the cost for holding inventory in stock is computed for time period (0, t₁) only.

Holding cost is as follows:

$$\begin{array}{l}\mathrm{HC}={\displaystyle {\int }_0^{{\mathit{t}}_1}h\left(t\right)I_1\left(t\right)}\\ \mathrm{HC}={\displaystyle {\int }_0^{{\mathit{t}}_1}\left(h+\mathit{\alpha t}\right)I_1\left(t\right)}\\ ={\displaystyle {\int }_0^{{\mathit{t}}_1}\left(h+\mathit{\alpha t}\right)e^{-\frac{\theta t^2}{2}}}{\displaystyle {\int }_t^{t_1}\left(a+\mathit{bu}\right)e^{\frac{\theta u^2}{2}}}\mathit{dudt}\\ =\left[\begin{array}{l}\mathit{ah}\left(\frac{1}{2}{t}_1^2+\frac{1}{12}\theta t_1^4+\frac{1}{90}\theta t_1^6\right)\\ +\mathit{bh}\left(\frac{1}{3}{t}_1^3+\frac{1}{15}\theta t_1^5+\frac{1}{105}\theta t_1^7\right)\\ +\mathit{a\alpha }\left(\frac{1}{6}{t}_1^3+\frac{1}{40}\theta t_1^5+\frac{1}{136}\theta t_1^7\right)\\ +\mathit{b\alpha }\left(\frac{1}{8}{t}_1^4+\frac{1}{48}\theta t_1^6+\frac{1}{384}\theta t_1^8\right)\end{array}\right].\end{array}$$

(6)

Shortage due to stock out is accumulated in the system during the interval (t₁, T).

The optimum level of shortage is present at t = T; therefore, the total shortage cost during this time period is as follows:

$$\begin{array}{l}\mathrm{SC}=C_2{\displaystyle {\int }_{{\mathit{t}}_1}^{\mathit{T}}-I_2\left(t\right)\mathit{dt}}\\ =\mathit{\beta a}{C}_2{\left(T-t_1\right)}^2+\frac{1}{2}\mathit{\beta b}{C}_2{\left(T-t_1\right)}^2\left(T+t_1\right).\end{array}$$

(7)

Due to stock out during (t₁, T), shortage is accumulated, but not all customers are willing to wait for the next lot size to arrive. Hence, this results in some loss of sale which accounts to loss in profit.

Lost sale cost is calculated as follows:

$$\begin{array}{l}\mathrm{LSC}=S{\displaystyle {\int }_{{\mathit{t}}_1}^{\mathit{T}}\left(1-\beta \right)D\left(t\right)\mathit{dt}}\\ \mathrm{LSC}=S\left(1-\beta \right)\left[a\left(T-t_1\right)+\frac{1}{2}b\left(T^2-t_1^2\right)\right].\end{array}$$

(8)

Purchase cost is as follows:

$$\begin{array}{l}\mathrm{PC}=\mathit{C}\left({\mathit{I}}_0+{\displaystyle {\int }_{{\mathit{t}}_1}^{\mathit{T}}\mathit{\beta D}\left(\mathit{t}\right)\mathit{dt}}\right)\\ \mathrm{PC}=\mathit{C}{\mathit{I}}_0+\mathit{C\beta a}\left(\mathit{T}-{\mathit{t}}_1\right)+\frac{1}{2}\mathit{C\beta a}\left({\mathit{T}}^2-{\mathit{t}}_1^2\right).\end{array}$$

(9)

Total cost is as follows:

$$\begin{array}{l}\mathrm{TC}=\mathrm{OC}+\mathrm{PC}+\mathrm{HC}+\mathrm{SC}+\mathrm{LSC}\\ \mathrm{TC}=\left[\begin{array}{l}A+C{I}_0+\mathrm{\beta C}+\left[a\left(T-t_1\right)+\frac{b}{2}\left(T^2-t_1^2\right)\right]\\ +\mathit{ah}\left[\frac{1}{2}{t}_1^2+\frac{1}{12}\theta t_1^4+\frac{1}{90}\theta t_1^6\right]\\ +\mathit{bh}\left[\frac{1}{3}{t}_1^3+\frac{1}{15}\theta t_1^5+\frac{1}{105}\theta t_1^7\right]\\ +\alpha a\left[\frac{1}{6}{t}_1^3+\frac{1}{40}\theta t_1^5+\frac{1}{136}\theta t_1^7\right]\\ +\alpha \mathrm{b}\left[\frac{1}{8}{t}_1^4+\frac{1}{48}\theta t_1^6+\frac{1}{136}\theta t_1^8\right]\\ +\beta {\mathrm{aC}}_2{\left(T-t_1\right)}^2+\frac{1}{2}\mathit{\beta b}{C}_2{\left(T-t_1\right)}^2\left(T+t_1\right)\\ +S\left(1-\beta \right)\left[a\left(T-t_1\right)+\frac{1}{2}b\left(T^2-t_1^2\right)\right]\end{array}\right].\end{array}$$

(10)

Differentiating Equation 10 with respect to t₁ and T, we then get the following:

$$\frac{\partial \mathrm{TC}}{\partial t_1}\mathrm{and}\frac{\partial \mathrm{TC}}{\partial T}.$$

To minimize the total cost TC(t₁, T) per unit time, the optimal value of T and t₁ can be obtained by solving the following equations:

$$\frac{\partial \mathrm{TC}}{\partial t_1}=0\mathrm{and}\frac{\partial \mathrm{TC}}{\partial T}=0,$$

(11)

providing that Equation 10 satisfies the following conditions:

$$\left(\frac{{\partial }^2\mathrm{TC}}{\partial t_1^2}\right)\left(\frac{{\partial }^2\mathrm{TC}}{\partial T^2}\right)-{\left(\frac{{\partial }^2\mathrm{TC}}{\partial t_1\partial T}\right)}^2>0\mathrm{and}\left(\frac{{\partial }^2\mathrm{TC}}{\partial t_1^2}\right)>0.$$

(12)

By solving (11), the value of T and t₁ can be obtained, and with the use of this optimal value, Equation 10 provides the minimum total inventory cost per unit time of the inventory system. Since the nature of the cost function is highly nonlinear, thus the convexity of the function is shown graphically in the next section.

Results and discussion

The following numerical values of the parameter in proper unit were considered as input for numerical and graphical analysis of the model, A = 2,500, a = 10, b = 50, C = 10, C₂ = 4, h = 0.5, θ = 0.8, α = 20, β = 0.8, and S = 8. The output of the model by using maple mathematical software (the optimal value of the total cost, the time when the inventory level reaches zero, and the time when the maximum shortages occur) is TC = 2,463.65, t₁ = 1.127, and T = 1.562.

If we plot the total cost function (10) with some values of t₁ and T such that fixed T at 1.562 and t₁ varies from 0.8 to 1.2, fixed t₁ at 1.127 and T varies from 1.2 to 1.8, and t₁ = 0.08 to 1.2 with equal interval T = 1.2 to 1.8, then we get the strictly convex graph of total cost function (TC) given by Figures 2, 3, 4, respectively.

Figure 2

Total cost vs. T at t ₁ = 0.1265.

Figure 3

Total cost vs. t ₁ at T = 0.1282.

Figure 4

Total cost vs. t ₁ and T .

The observation from Figures 2, 3, 4 is that the total cost function is a strictly convex function. Thus, the optimum value of T and t₁ can be obtained with the help of the total cost function of the model provided that the total inventory cost per unit time of the inventory system is minimum.

Conclusion

This paper presents an inventory model of direct application to the business enterprises that consider the fact that the storage item is deteriorated during storage periods and in which the demand, deterioration, and holding cost depend upon the time. In this paper, we developed a deterministic inventory model with time-dependent demand and time-varying holding cost where deterioration is time proportional. The model allows for shortages, and the demand is partially backlogged. The model is solved analytically by minimizing the total inventory cost. Finally, the proposed model has been verified by the numerical and graphical analysis. The obtained results indicate the validity and stability of the model. The proposed model can further be enriched by taking more realistic assumptions such as finite replenishment rate, probabilistic demand rate, etc.