Hostname: page-component-8448b6f56d-jr42d Total loading time: 0 Render date: 2024-04-19T23:32:38.690Z Has data issue: false hasContentIssue false
  • English
  • Français

Large deviations for supercritical multitype branching processes

Part of: Markov processes Limit theorems

Published online by Cambridge University Press:  14 July 2016

Owen Dafydd Jones
Owen Dafydd Jones*
Affiliation:
University of Southampton
Get access Rights & Permissions [Opens in a new window]

Abstract

Large deviation results are obtained for the normed limit of a supercritical multitype branching process. Starting from a single individual of type i, let L[i] be the normed limit of the branching process, and let 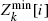be the minimum possible population size at generation k. If 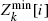is bounded in k (bounded minimum growth), then we show that P(L[i] ≤ x) = P(L[i] = 0) + x α F *[i](x) + o(x α ) as x → 0. If 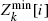grows exponentially in k (exponential minimum growth), then we show that −log P(L[i] ≤ x) = x −β/(1−β) G*[i](x) + o (x −β/(1−β)) as x → 0. If the maximum family size is bounded, then −log P(L[i] > x) = x δ/(δ−1) H *[i](x) + o(x δ/(δ−1)) as x → ∞. Here α, β and δ are constants obtained from combinations of the minimum, maximum and mean growth rates, and F *, G * and H * are multiplicatively periodic functions.

Keywords

Branching processmultitypelarge deviation

MSC classification

Primary: 60J80: Branching processes (Galton-Watson, birth-and-death, etc.)
Secondary: 60F10: Large deviations
Type
Research Papers
Information
Journal of Applied Probability , Volume 41 , Issue 3 , September 2004 , pp. 703 - 720
Copyright
Copyright © Applied Probability Trust 2004 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Athreya, K. B. (1994). Large deviation rates for branching processes. I. Single type case. Ann. Appl. Prob. 4, 779–790.10.1214/aoap/1177004971Google Scholar
Athreya, K. B., and Vidyashankar, A. N. (1995). Large deviation rates for branching processes. II. The multitype case. Ann. Appl. Prob. 5, 566–576.10.1214/aoap/1177004778Google Scholar
Athreya, K. B., and Vidyashankar, A. N. (1997). Large deviation rates for supercritical and critical branching processes. In Classical and Modern Branching Processes (IMA Vol. Math. Appl. 84), eds Athreya, K. B. and Jagers, P., Springer, New York, pp. 1–18.10.1007/978-1-4612-1862-3Google Scholar
Biggins, J. D. (2001). The growth of iterates of multivariate generating functions. Preprint, University of Sheffield.Google Scholar
Biggins, J. D., and Bingham, N. H. (1991). Near-constancy phenomena in branching processes. Math. Proc. Camb. Phil. Soc. 110, 545–558.10.1017/S0305004100070614Google Scholar
Biggins, J. D., and Bingham, N. H. (1993). Large deviations in the supercritical branching process. Adv. Appl. Prob. 25, 757–772.10.2307/1427790Google Scholar
Bingham, N. H. (1988). On the limit of a supercritical branching process. In A Celebration of Applied Probability (J. Appl. Prob. Spec. Vol. 25A), ed. Gani, J., Applied Probability Trust, Sheffield, pp. 215–228.Google Scholar
Dubuc, M. S. (1971). La densité de la loi-limite d'un processus en cascade expansif. Z. Wahrscheinlichkeitsth. 19, 281–290.10.1007/BF00535833Google Scholar
Dubuc, S. (1971). Problèmes relatifs à l'itération des fonctions suggérés par les processus en cascade. Ann. Inst. Fourier 21, 171–251.10.5802/aif.365Google Scholar
Ellis, R. S. (1984). Large deviations for a general class of random vectors. Ann. Prob. 12, 1–12.10.1214/aop/1176993370Google Scholar
Gärtner, J. (1977). On large deviations from the invariant measure. Theory Prob. Appl. 22, 24–39.10.1137/1122003Google Scholar
Hambly, B. M., and Jones, O. D. (2002). Asymptotically one-dimensional diffusion on the Sierpinski gasket and multitype branching processes with varying environment. J. Theoret. Prob. 15, 285–322.10.1023/A:1014858709284Google Scholar
Hambly, B. M., and Jones, O. D. (2003). Thick and thin points for random recursive fractals. Adv. Appl. Prob. 35, 251–277.10.1239/aap/1046366108Google Scholar
Harris, T. E. (1948). Branching processes. Ann. Math. Statist. 19, 474–494.10.1214/aoms/1177730146Google Scholar
Hoppe, F. M. (1976). Supercritical multitype branching processes. Ann. Prob. 4, 393–401.10.1214/aop/1176996088Google Scholar
Jones, O. D. (2002). Multivariate Böttcher equation for polynomials with nonnegative coefficients. Aequationes Math. 63, 251–265.10.1007/s00010-002-8023-7Google Scholar
Liu, Q. (1996). The growth of an entire characteristic function and tail probabilities of the limit of a tree martingale. In Trees (Prog. Prob. 40), eds Chauvin, B. Cohen, S. and Rouault, A., Birkhäuser, Basel, pp. 51–80.10.1007/978-3-0348-9037-3_5Google Scholar
Liu, Q. (1999). Asymptotic properties of supercritical age-dependent branching processes and homogeneous branching random walks. Stoch. Process. Appl. 82, 61–87.10.1016/S0304-4149(99)00008-3Google Scholar
Ryan, T. A. (1976). A multidimensional renewal theorem. Ann. Appl. Prob. 4, 656–661.10.1214/aop/1176996034Google Scholar