Abstract
The role of Tsalli's non-extensive Information Measure within an à la Jaynes Information-Theory-based formulation of Statistical Mechanics is discussed in rather detailed fashion.
Tsallis entropy and Jaynes' Information Theory formalism* * This work is dedicated to the memory of Prof. E. T. Jaynes, who passed away on 30 April 1998.
A. Plastino1, 2 and A. R. Plastino1,2
1 National University La Plata
C.C. 727, 1900 La Plata, Argentina
2 Argentine National Research Council (CONICET)
Received 07 December, 1998
The role of Tsalli's non-extensive Information Measure within an à la Jaynes Information-Theory-based formulation of Statistical Mechanics is discussed in rather detailed fashion.
I Introduction
In spite of its great success, the Statistical Mechanics paradigm based on the Boltzmann-Gibbs entropy measure seems to be inadequate to deal with many interesting physical scenarios [1, 2, 3]. Astronomical self-gravitating systems constitute an important illustrative example of these difficulties [4]. A considerable effort has been devoted by astrophysicists to develop a thermostatistical description of self-gravitating systems along the lines of standard Statistical Mechanics. The failure of those attemps was due to the nonextensivity effects associated with the long range of the gravitational interaction [4].
Ten years ago Tsallis proposed a generalization of the celebrated Boltzmann-Gibbs (BG) entropic measure [5]. The new entropy functional introduced by Tsallis [5] along with its associated generalized thermostatistics [6, 7] is nowadays being hailed as the possible basis of a theorethical framework aproppriate to deal with nonextensive settings [8, 9, 10]. This entropy has the form
where x is a dimensionless state-variable, f corresponds to the probability distribution and the entropic index q is any real number. This entropy recovers the standard Boltzmann-Gibbs entropy S = - ò f ln f dx in the limit q® 1. Sq is nonextensive such that Sq(A+B) = Sq(A) + Sq(B) + (1-q)Sq(A)Sq(B), where A and B are two systems independent in the sense that f(A+B) = f(A)f(B). It is clear that q can be seen as measuring the degree of nonextensivity.
Many relevant mathematical properties of the standard thermostatistics are preserved by Tsallis' formalism or admit natural generalizations [8-14]. Tsallis' proposal was shown to be consistent both with Jaynes' Information Theory formulation of statistical mechanics [15], and with the dynamical thermostatting approach to statistical ensembles [16].
The recent application of Tsallis' theory to an increasing number of physical problems is begining to provide a picture of the kind of scenarios where the new formalism is useful. Self-gravitating systems constituted the first physical problem discussed within the nonextensive thermostatistics [17]. That early application, in turn, inspired Boghosian's treatment of the two dimensional pure electron plasma, yielding the first experimental confirmation of Tsallis theory [18]. A possible solution of the solar neutrino puzzle based on Tsallis thermostatistics has been advanced [19]. Some cosmological implications of Tsallis proposal have also been worked out [20]. The behaviour of dissipative low dimensional chaotic systems [21], as well as self organized critical systems [22] have been discussed in connection with the new approach. Tsallis entropy has also been advanced as the basis of a thermostatistical foundation of Lévy flights and distributions [23]. Tsallis nonextensive statistical formalism proved to be a useful framework for the analysis of many interesting properties of nonlinear Fokker-Planck equations [24-29]. It has been shown that Tsallis maximum entropy (MaxEnt) distributions can also arise naturally as stationary solutions of linear Fokker-Planck equations [30].
Tsallis bold attempt to develope a complete thermostatistical formalism on the basis of a nonlogarithmic entropy functional has raised many interesting issues related both to the mathematical structure and physical implications of general thermostatistical formalisms [31, 32]. Tsallis pioneering work has stimulated the exploration of the properties of other generalized or alternative information measures [33, 34]. On the other hand, it has been recently realized that some important features are shared by extended families of thermostatistical formalism [31, 32].
Tsallis' theory can be elegantly formulated in terms of Jaynes' Information Theory (IT) approach to Statistical Mechanics. It is our purpose here that of reviewing this type of formulation, that helps placing Tsallis' thermostatistics in an adequate context.
II Basic ideas of Jaynes' IT approach
III The maximum entropy probability distribution
Information Theory (IT) [35] provides one with a powerful inference methodology in order to describe general properties of arbitrary systems on the basis of scarce information. Indeed, it purports to yield the least-biased description that can be devised on the basis of some specific data, in any possible situation. Within a Statistical Mechanics'context Jaynes [36-39] was able to employ IT ideas so as to reformulate and generalize the basic foundations of the field, in what constituted a rather spectacular advance. The essential ideas underlying Jaynes' IT-based methodology [36-39] can best be introduced with reference to the following, quite general environment. Let Ar, (r = 1, ¼, M) be a set of (real) random variables that characterize some system S of interest. These variables adopt the (possible) values Ar(i) with (properly normalized) probabilities p(i), where i = 1, ¼, N enumerates the possible "states" of S. Assume now that our "experimental" information concerning S is limited to the set of mean values("expectation" values)
The question to be answered is the following one: what can we assert concerning the (unknown) probability distribution {p(i)}? As, in general, M < N (indeed, in most realistic situations we have M << N), many different distributions {p(i)} are compatible with the information supply (2). However, IT claims that the BEST (or least-biased) one is precisely that which maximizes the Thermodynamical entropy [36-39]). We see that in order to find this purportedly "one and only" {p(i)} we face an extremalization problem of the Lagrange sort, in which one extremalizes a given functional S, subject to a set of constraints, i.e., Eqs. (2) (our "input" or "prior" knowledge) supplemented by the normalization condition
As we deal with M + 1 constraints we must introduce an equal number of Lagrange multipliers, that we shall denote by l0-1, lr, (r = 1, ¼, M) and freely extremalize
that is, we set
for any arbitrary dp(i), which entails that
so that, on the basis of the prior information (Eqs. (2) and (3) we infer the distribution {p(i)} of the typical exponential (which guarantees the essential positivity requirement on the distribution) appearance
We introduce now the useful abbreviation
for any (analytical) function f of the Ar(i). For example, we have
We define now the "partition" function
which, on account of (3) leads immediately to
i.e.,
a pair of relationships that will be frequently encountered herefrom. The first derivative of (12) yields
which, when properly interpreted, solves our variational problem, as we now proceed to show. Notice that, in (8), lr, r = 1, ¼, M are the only variables. Consequently, Z is a function of these M Lagrange multipliers. So is then l0, in view of (12)
We should then regard (14) as a set of (coupled) highly non-linear equations in the M variables lr, with the input-information (the < Ar > ) on the r.h.s. When solved, this system provides us with Z and the Maximum Entropy {p(i)}.
IIII The main properties of the Maximum Entropy Probability (MEP) distribution
Our maximum entropy (or maximum ignorance) acquires the aspect
On the basis of (12) and (15) we readily ascertain that l0 and S are related by means of a quite general Legendre transform [36, 37, 38, 39]
which clearly tells us that, as Z is a function of the Legendre multipliers, S must be a function of the mean values. This mathematical result is consistent with Shannon's interpretation of S as a missing information function, that is, S measures our ignorance once the < Ar > are given. In addition to (14) we write then
We can define also a generalized "free energy" by selecting a special Lagrange multiplier, say ls, and writing
with
positive, maximizing S is tantamount to minimizing Fs. From (15) we also obtain
the relation "conjugate" to (14). See also that
and that
which leads to
We can also write
which, in the particular case of having M = 1 specializes to
so that the derivative of the entropy with respect to l1 gives immediately the dispersion.
III The modified Kinchin axiomatics
One of the salient contributions of Information Theory (IT) is that of yielding a recipe for ascertaining in precise and unambiguous terms the amount of information (the information measure) that an observer possesses concerning a given phenomenon when only a probability distribution (PD) is known. The informational content of a normalized probability distribution P(i),(i = 1, ¼, N), where the subindex i runs over the states of the system one is trying to study, is given by Shannon's information measure (IM) [35]
where the choice of the logarithm basis is used to fix the informational units. If the basis is 2 then S is measured in bits.
In a more formal vein one is led to consider Kinchin Axioms [40] as providing the conceptual foundations of Information Theory. Consider a system S composed of two subsytems (S1, S2). Let  be a PD associated to subsystem Sm (m = 1, 2). The PD corresponding to the total system is labelled by two subindexes i, j, one for each of the subsytems. In general, the two subsystems will be correlated, so that one needs the conditional probability Q(j|i) of finding S2 in state j when one is sure that the state of S1 is that labelled by i, and a concomitant conditional IM, expressed in terms of Q(j |i). Kinchin axioms read
be a PD associated to subsystem Sm (m = 1, 2). The PD corresponding to the total system is labelled by two subindexes i, j, one for each of the subsytems. In general, the two subsystems will be correlated, so that one needs the conditional probability Q(j|i) of finding S2 in state j when one is sure that the state of S1 is that labelled by i, and a concomitant conditional IM, expressed in terms of Q(j |i). Kinchin axioms read
1) For a system S described by a PD P(i), i = 1, ¼, N, the IM is a function only of the P(i)
2) For such a system S{P} £ S{uniform PD}, where the uniform PD is, of course,  , for all i.
, for all i.
3) Suppose that, instead of dealing with N states we confront N+1 ones, with the proviso that P(N+1) = 0. Then S does not change.
4) Let S be composed of two subsystems, as explained above. Then
These four axioms lead in univocal fashion to Shannon's IM (28). To most people, the first three axioms appear self-evident. However, the last one does not seem to enjoy the same status. One may think that a more natural phrasing of the fourth axiom would be
4')
but the ensuing, modified set of axioms leads not to just one but to two IM's. One of them is Shannon's. The other reads
which is known as Rény's IM and has found extensive applications in connection with fractals and Cantor sets [41].
Jaynes [36] has shown that if one chooses Boltzmann's constant as the informational unit and identifies Shannon's IM with the Thermodynamical entropy, then the whole of Statistical Mechanics can be elegantly reformulated, without any reference to the notion of ensemble, by extremalization of Shannon's S, subject to the constraints posed by the a priori information one may possess concerning the system of interest (the Maximum Entropy Principle (MEP)) [37, 38, 39]. Rény's IM [42] cannot be regarded as a physical entropy, as it does not have a definite concavity when expressed as a function of the pertinent P(i).
Can we think of still an alternative version of the fourth postulate that will yield an IM of definite concavity different from Shannon's one? If we advance the following axiom [7]
4'')
one is led to Tsallis's entropy [1, 2, 3, 7]
and is related to Rény's IM Sq(R) in the following fashion
IV Tsallis' generalized statistical mechanics
Within a classical Gibbsian context, Tsallis [1, 2, 3, 7] showed that his entropy leads to a Generalized Statistical Mechanics (GSM). Consider a system S with M possible microscopic configurations and let { pi } stand for the probability of finding the system in the configuration i. As stated above, the associated Tsallis' IM, to be regarded herefrom as a physical entropy, reads
with q a real parameter (we have a different statistics for every possible q-value) and
In order to study the limit q ® 1 we write
and find that for q ® 1
i.e., for q = 1 Tsallis' entropy coincides with the Gibbs-Shannon one.
From its definition Sq ³ 0. Sq vanishes (for all q) in the case M = 1, and, for M > 1, q > 0, whenever one of the pi equals unity and the remaining ones, of course, vanish. A global, absolute maximum of Sq (for all q) obtains, according to the modified Kinchin's axioms, in the case of equiprobability, when all pi = 1/M. In such an instance we have
that, in the limit q ® 1 leads to the celebrated Boltzmann expression
Tsallis' entropy exhibits a series of notable properties that reiforce the idea that Sq is indeed a physical quantity. We list some of them below.
IV.1 Concavity
Let us consider two PD's {  } and {
} and {  } , where i labels the members of a set of M microstates. For a real l such that 0 < l < 1 we define an "intermediate" distribution { pi } by recourse to
} , where i labels the members of a set of M microstates. For a real l such that 0 < l < 1 we define an "intermediate" distribution { pi } by recourse to
One easily verifies that
The functional Sq[pi] is concave for q > 0 and convex for q < 0 (Sq being constant ( = M-1) for q = 0).
IV.2 Pseudo-aditivity
Consider two independent systems A and B characterized by possessing Ma and Mb microstates, respectively and assume that the corresponding PD's are
The total, composite system A È B (of microstates given by all possible pairs of A- and de B-microstates ) is described by the PD
and one easily finds that its associated entropy is
As a consequence we have
so that, except for q = 1, Tsallis' entropy is a non-extensive quantity, this being its main difference vis-a-vis the orthodox one.
IV.3 Canonical ensemble
Tsallis found that by extremalization of Sq under the constraints posed by both normalization and assumed knowledge of the internal energy, that is
one obtains the generalized canonical distribution [15]
where
is the generalized partition function.
However, more interesting results obtain if one introduces as contraint the generalized internal energy [2]
which leads to the PD
with
Curado and Tsallis [6] found that the whole mathematical (Legendre-transform based) structure of thermodynamics becomes in this fashion invariant under a change of the q-value (from unity to any other real number). Indeed, one finds, for example, relations of the form
identical to their well-known q = 1-counterparts if one replaces ln Z by
One immediately realizes that
are related by a Legendre transform.
V Generalized Entropies and Information Theory
Plastino and Plastino [15] have generalized the work of ref. [6] by 1) embbeding it within a purely quantal (Hilbert space) context and 2) using Jaynes' approach to SM, which allows one to deal with (the IT equivalent of) any ensemble, accomodating both equilibrium and off-equilibrium situations on an equal footing.
The first step in that direction is, of course, the construction of a statistical operator (or density operator, or density matrix)  able to account for all the available information, on the one hand, and that maximizes Tsallis' entropy, on the other one. The available (a priori or prior) information can (in general) be casted in the form of a set of expectation values (EV). Here we need, however, generalized EV's, in the spirit of Curado and Tsallis [6] (see above the definition of a generalized internal energy). We assume prior knowledge of M EV's, corresponding to M operators
able to account for all the available information, on the one hand, and that maximizes Tsallis' entropy, on the other one. The available (a priori or prior) information can (in general) be casted in the form of a set of expectation values (EV). Here we need, however, generalized EV's, in the spirit of Curado and Tsallis [6] (see above the definition of a generalized internal energy). We assume prior knowledge of M EV's, corresponding to M operators  ,
,
where, we insist, generalized EV's are being employed, according to the definition
with an ordinary EV on the r.h.s. Of course, normalization entails
After a bit of algebra, recourse to that Lagrange multipliers method provides us with the normalized density operator that reproduces the M known (generalized) EV's (Cf Eq. (60)) and maximizes Tsallis' entropy. One finds [7]
where Z is the partition function
and we have M Lagrange multipliers li that guarantee compliance with the M EV-related constraints. However, a small dificulty remains. The density operator is a definite positive one and, as it stands, this is not guaranteed by Eq. (63). Consequently, we must require that the operator
appearing between the parenthesis in (63) be a positive definite one. This entails that the eigenvalues of  must be non-negative quantities. An ad-hoc requirement (to be justified below) is then to be introduced at this point. An heuristic cut-off is needed. Instead of (63) we write
must be non-negative quantities. An ad-hoc requirement (to be justified below) is then to be introduced at this point. An heuristic cut-off is needed. Instead of (63) we write
with Z given by
and Q(x) the step (Heaviside's) function
Equations (66-67) should be interpreted as follows. Let | i > and ai, respectively, the eigenvectors and eigenvalues of the operator (66), so that (spectral decomposition)
In this special basis  adopts the appearance
adopts the appearance
with f(x) defined according to
Using now the shorthand notation
and
the generalized entropy Sq is given by
Obviously, the operators  and
and  commute. Thus, their product can be expressed in the common basis that diagonalizes them. Assuming this has been done, a bit of contemplative reflection should convince one that
commute. Thus, their product can be expressed in the common basis that diagonalizes them. Assuming this has been done, a bit of contemplative reflection should convince one that
where, of course, all negative eigenvalues (of  ) have been conveniently dropped (our cut-off). With a clear conscience we can now write
) have been conveniently dropped (our cut-off). With a clear conscience we can now write
Now, from the very definition of the generalized entropy Sq we have,
so that (76) and (77) yield the Generalized Euler's Theorem [15]
where the Jaynes parameter lJ is given by
The parameter (79) plays, within this generalized context, the role of the logarithm of the partition function in the orthodox SM.
Generalized EV's á ñq , Jaynes parameter lJ, and the Lagrange multipliers li obey certain strictures that constitute the heart of a thermodynamical description. Partial derivation of lJ with respect to the li (i = 1, ¼, M) yields (consider here that our primed operator is
ñq , Jaynes parameter lJ, and the Lagrange multipliers li obey certain strictures that constitute the heart of a thermodynamical description. Partial derivation of lJ with respect to the li (i = 1, ¼, M) yields (consider here that our primed operator is 
which leads to
that, together with Euler' theorem, tell us that
and allows for the very important result [15]
Equations (81) and (83) constitute the basic IT relations in order to build up quantum SM à la Jaynes. In deriving them we reach the result that the whole of quantum SM is invariant under a change of q (from unity to any other real number).
The generalized EV's can be shown to obey an Ehrenfest's theorem [15]. Consider a density operator  (t) (not necessarily of the maximum entropy form) that evolves (in time) according to Von Neumann' equation
(t) (not necessarily of the maximum entropy form) that evolves (in time) according to Von Neumann' equation
where  is the system's hamiltonian. Let | fi(t) > and ai be, respectively, the eigenvectors and eigenvalues of
is the system's hamiltonian. Let | fi(t) > and ai be, respectively, the eigenvectors and eigenvalues of  . According to (84) the latter do not depend upon the time while the | fi(t) > are solutions of Schroedinger's equation
. According to (84) the latter do not depend upon the time while the | fi(t) > are solutions of Schroedinger's equation
From the time-independent nature of the ai one gathers that if
is a solution of Von Neumann's equation, another such solution is given by
Thus, if
q fulfills Von Neumann's strictures, the generalized EV's á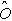 ñq will necessarily verify Ehrenfest's theorem [15]
ñq will necessarily verify Ehrenfest's theorem [15]
VI Justifying Tsallis' formalism
Plastino and Plastino [43] have justified the GSM discussed above with reference to an argument similar to that employed by Gibbs himself in deriving his canonical ensemble. The idea is to go back to Gibbs' microcanonical ensemble (GME).
Consider a system S with energy levels denoted by ei, weakly interacting with a thermal bath B and assume one describes the "total" system T = S+B by recourse to the GME when its total energy E lies in the interval
with
As usual, the energy spectrum of the bath B is regarded as being of a quasi-continuous character. Plastino and Plastino [43] traverse a new road, however, in assuming that B is a finite system, of finite energy Eb.
As the total system T is microcanonically described, the probability pi of finding S in a state ||i > of energy ei is proportional to the total number n of T-configurations compatible with such a situation. In view of the quasicontinuous character of the B-energy spectrum, n will be given by
where h(E) represents the number of states (per unit energy interval) of B in a neighbourhood of E . Thus,
Let us assume that the number of states M(E) of B with energy smaller ( or equal) than E grows as a power a of E. Such a growth-law is often encountered. As examples we mention
a) A set of N independent harmonic oscillators (a = N),
b) A set of N free (nonrelativistic) particles confined in a D-dimensional box (a = DN/2),
c) A set of N plane, rigid rotators (a = N/2).
With this last assumption we find
because h(E) is essentially the derivtive of M(E) with respect to E. Thus
so that, after multiplication by the convenient normalization factor Z-1, with
we arrive at
Setting
and
we obtain Tsallis' canonical distribution
with
q being, of course, Tsallis' characteristic parameter. In the limit q ® 1 one recovers Gibbs' conventional expressions
The physical meaning of the q® 1 limit deserves special attention. So as to fix ideas let us consider that our thermal bath consists of N independent Harmonic oscillators (a = N). Eqs. (97)-(98) give
and
The limit q ® 1 corresponds to that situation characterized by N ® ¥ and E0® ¥, the process proceeding in such a fashion as to keep constant the energy per oscillator W = E0/N. Consequently, Tsallis' generalized canonical distribution describes a systema in thermal contact with a finite reservoir. Stricto sensu, infinte baths do not exist in nature, so that, in some sense, Tsallis' distribution can be regarded as the natural one, Gibbs' being, instead, a convenient mathematical ïdealization".
The interpretation given in [43] to Tsallis GSM allows one to conclude:
1.- The values adopted by Tsallis' parameter q are determined by the nature of the appropriate thermal bath
2.- The cut-off ad-hoc condition needed so as to determine Tsallis' statistical operator appears here in a natural fashion. The probability pi associated to the microstate ||i > vanishes whenever
which is equivalent to the condition
Obviously, (106) implies pi = 0: the energy of the system S cannot exceed E0, that of the total system T = S+B.
References
-
[1]
- C. Tsallis, Physica A 221, 277 (1995). [2]
- C. Tsallis, Chaos, Solitons, and Fractals 6, 539 (1995), and references therein; an updated bibliography can be found in http://tsallis.cat.cbpf.br/biblio.htm [3]
- C. Tsallis, Physics World 10, 42 (July 1997). [4]
- A.R. Plastino and A. Plastino, in Condensed Matter Theories, Volume 11, E. Ludeña (Ed.), Nova Science Publishers, New York, USA, p. 341 (1996). [5]
- C. Tsallis, J. Stat. Phys. 52, 479 (1988). [6]
- E.M.F. Curado and C. Tsallis, J. Phys. A24, L69 (1991); Corrigenda: 24, 3187 (1991) and 25, 1019 (1992). [7]
- A.R. Plastino and A. Plastino, in Condensed Matter Theories, Volume 11, E. Ludeña (Ed.), Nova Science Publishers, New York, USA, p. 327 (1996). [8]
- D.H. Zanette and P.A. Alemany, Phys. Rev. Lett. 75, 366 (1995); M.O. Caceres and C.E. Budde, ibid 77, 2589 (1996); D.H. Zannette and P.A. Alemany, ibid 77, 2590 (1996). [9]
- A.K. Rajagopal, Phys.Rev.Lett. 76, 3469 (1996). [10]
- E.K. Lenzi, L.C. Malacarne and R.S. Mendes, Phys. Rev. Lett. 80, 218 (1998). [11]
- A. R. Plastino, A. Plastino and C. Tsallis, J. Phys. A, 27, 5707, (1994). [12]
- G. A. Raggio, J. Math. Phys. 36, 4785 (1995). [13]
- A. M. Meson and F. Vericat, J. Math. Phys. 37, 4480 (1996). [14]
- R. J. V. dos Santos, J. Math. Phys. 38, 4104 (1997). [15]
- A. R. Plastino and A. Plastino, Phys. Lett. A177, 177 (1993). [16]
- A.R. Plastino and C. Anteneodo, Ann. Phys. 255, 250 (1997). [17]
- A. R. Plastino and A. Plastino, Phys. Lett. A174, 384 (1993); J.J. Aly, in "N-Body Problems and Gravitational Dynamics", Proc. of the Meeting held at Aussois-France (21-25 March 1993), eds. F. Combes and E. Athanassoula (Publications de l'Observatoire de Paris, 1993). [18]
- B. M. R. Boghosian, Phys. Rev. E 53, 4754 (1995); C. Anteneodo and C. Tsallis, J. Mol. Liq. 71, 255 (1997). [19]
- G. Kaniadakis, A. Lavagno and P. Quarati, Phys. Lett. B 369, 308 (1996); P. Quarati, A. Carbone, G. Gervino, G. Kaniadakis, A. Lavagno and E. Miraldi, Nucl. Phys. A 621, 345c (1996). [20]
- V.H. Hamity and D.E. Barraco, Phys. Rev. Lett. 76, 4664 (1996); D.F. Torres, H. Vucetich and A. Plastino, Phys. Rev. Lett. 79 1588 (1997). [21]
- C. Tsallis, A.R. Plastino and W.-M. Zheng, Chaos, Solitons and Fractals 8, 885 (1997); M. L. Lyra and C. Tsallis, Phys. Rev. Lett. 80, 53 (1998). [22]
- F.A. Tamarit, S.A. Cannas and C. Tsallis, European Phys. J. B (1998), in press; A.R.R. Papa and C. Tsallis, Imitation Games: Power Law Sensitivity to Initial Conditions and Nonextensivity, Phys. Rev. E, (1998), in press. [23]
- P. A. Alemany and D. H. Zanette, Phys. Rev. E49, 956 (1994); C. Tsallis, S.V.F. Levy, A.M.C. Souza and R. Maynard, Phys. Rev. Lett. 75, 3589 (1995); Erratum: 77, 5442 (1996). [24]
- A. R. Plastino and A. Plastino, Physica A 222, 347 (1995). [25]
- C. Tsallis and D. J. Bukman, Phys. Rev. E 54, R2197 (1996). [26]
- L. Borland, Phys. Rev. E 57, 6634 (1998). [27]
- D.A. Stariolo, Phys. Rev. E 55, 4806 (1997). [28]
- A. Compte and D. Jou, J. Phys. A 29, 4321 (1996). [29]
- A. Compte, D. Jou, and Y. Katayama, J. Phys. A 30, 1023 (1997). [30]
- L. Borland, Ito-Langevin Equation within Generalized Thermostatistics, Phys. Lett A (1998), in press. [31]
- A. Plastino and A.R. Plastino, Phys. Lett. A 226, 257 (1997). [32]
- R.S. Mendes, Physica A 242, 299 (1997). [33]
- Andrés R.R. Papa, J. Phys. A: Math. Gen. 31, 5271 (1998). [34]
- S. Abe, Phys. Lett. A 224, 326 (1997). [35]
- C. Shannon and W. Weaver, The Mathematical Theory of Communication, University of Illinois Press, Urbana (1948) [36]
- Jaynes E.T., Phys. Rev. 106, 620 (1957); 118, 171 (1961). [37]
- E. T. Jaynes in Papers on probability, statistics and statistical physics, edited by R. D. Rosenkrantz (Reidel, Dordrecht, Holland, 1983). [38]
- Brillouin, L., Science and Information Theory, Academic Press, New York (1956). [39]
- W. T. Grandy, Jr., and P. W. Milonni, Physics and probability: Essays in honor of E. T. Jaynes (Cambridge University Press, Cambridge, England, 1993). [40]
- A. I. Kinchin, Mathematical Foundations of Information Theory, Dover Publ., New York (1957). [41]
- C. Beck and F. Schögl, Thermodynamics of chaotic systems (Cambridge University Press, Cambridge, England, 1993). [42]
- A. Rényi, Probability theory (North-Holland, Amsterdam, 1970). [43]
- A. R. Plastino and A. Plastino, Phys. Lett. A 193, 251 (1994).
- [1] C. Tsallis, Physica A 221, 277 (1995).
- [2] C. Tsallis, Chaos, Solitons, and Fractals 6, 539 (1995),
- [3] C. Tsallis, Physics World 10, 42 (July 1997).
- [4] A.R. Plastino and A. Plastino, in Condensed Matter Theories, Volume 11, E. Ludeńa (Ed.), Nova Science Publishers, New York, USA, p. 341 (1996).
- [5] C. Tsallis, J. Stat. Phys. 52, 479 (1988).
- [6] E.M.F. Curado and C. Tsallis, J. Phys. A24, L69 (1991);
- [7] A.R. Plastino and A. Plastino, in Condensed Matter Theories, Volume 11, E. Ludeńa (Ed.), Nova Science Publishers, New York, USA, p. 327 (1996).
- [8] D.H. Zanette and P.A. Alemany, Phys. Rev. Lett. 75, 366 (1995);
- [9] A.K. Rajagopal, Phys.Rev.Lett. 76, 3469 (1996).
- [10] E.K. Lenzi, L.C. Malacarne and R.S. Mendes, Phys. Rev. Lett. 80, 218 (1998).
- [11] A. R. Plastino, A. Plastino and C. Tsallis, J. Phys. A, 27, 5707, (1994).
- [12] G. A. Raggio, J. Math. Phys. 36, 4785 (1995).
- [13] A. M. Meson and F. Vericat, J. Math. Phys. 37, 4480 (1996).
- [14] R. J. V. dos Santos, J. Math. Phys. 38, 4104 (1997).
- [15] A. R. Plastino and A. Plastino, Phys. Lett. A177, 177 (1993).
- [16] A.R. Plastino and C. Anteneodo, Ann. Phys. 255, 250 (1997).
- [17] A. R. Plastino and A. Plastino, Phys. Lett. A174, 384 (1993);
- [18] B. M. R. Boghosian, Phys. Rev. E 53, 4754 (1995);
- [19] G. Kaniadakis, A. Lavagno and P. Quarati, Phys. Lett. B 369, 308 (1996);
- [20] V.H. Hamity and D.E. Barraco, Phys. Rev. Lett. 76, 4664 (1996);
- [21] C. Tsallis, A.R. Plastino and W.-M. Zheng, Chaos, Solitons and Fractals 8, 885 (1997);
- [22] F.A. Tamarit, S.A. Cannas and C. Tsallis, European Phys. J. B (1998), in press;
- A.R.R. Papa and C. Tsallis, Imitation Games: Power Law Sensitivity to Initial Conditions and Nonextensivity, Phys. Rev. E, (1998), in press.
- [23] P. A. Alemany and D. H. Zanette, Phys. Rev. E49, 956 (1994);
- [24] A. R. Plastino and A. Plastino, Physica A 222, 347 (1995).
- [25] C. Tsallis and D. J. Bukman, Phys. Rev. E 54, R2197 (1996).
- [26] L. Borland, Phys. Rev. E 57, 6634 (1998).
- [27] D.A. Stariolo, Phys. Rev. E 55, 4806 (1997).
- [28] A. Compte and D. Jou, J. Phys. A 29, 4321 (1996).
- [29] A. Compte, D. Jou, and Y. Katayama, J. Phys. A 30, 1023 (1997).
- [30] L. Borland, Ito-Langevin Equation within Generalized Thermostatistics, Phys. Lett A (1998), in press.
- [31] A. Plastino and A.R. Plastino, Phys. Lett. A 226, 257 (1997).
- [32] R.S. Mendes, Physica A 242, 299 (1997).
- [33] Andrés R.R. Papa, J. Phys. A: Math. Gen. 31, 5271 (1998).
- [34] S. Abe, Phys. Lett. A 224, 326 (1997).
- [35] C. Shannon and W. Weaver, The Mathematical Theory of Communication, University of Illinois Press, Urbana (1948)
- [36] Jaynes E.T., Phys. Rev. 106, 620 (1957);
- [37] E. T. Jaynes in Papers on probability, statistics and statistical physics, edited by R. D. Rosenkrantz (Reidel, Dordrecht, Holland, 1983).
- [38] Brillouin, L., Science and Information Theory, Academic Press, New York (1956).
- [39] W. T. Grandy, Jr., and P. W. Milonni, Physics and probability: Essays in honor of E. T. Jaynes (Cambridge University Press, Cambridge, England, 1993).
- [40] A. I. Kinchin, Mathematical Foundations of Information Theory, Dover Publ., New York (1957).
- [41] C. Beck and F. Schögl, Thermodynamics of chaotic systems (Cambridge University Press, Cambridge, England, 1993).
- [42] A. Rényi, Probability theory (North-Holland, Amsterdam, 1970).
- [43] A. R. Plastino and A. Plastino, Phys. Lett. A 193, 251 (1994).
Publication Dates
-
Publication in this collection
17 Sept 1999 -
Date of issue
Mar 1999
History
-
Received
07 Dec 1998





































































































