Abstract
Several aspects of the Thermodynamics of systems away from equilibrium are considered. Particular attention is given to the question of the concepts of entropy and temperature in arbitrary nonequilibrium conditions. Even though such state function and thermodynamic variable are elusive in such conditions, it is elaborated and discussed an approach to them that can be obtained in the framework of the so-called Informational Statistical Thermodynamics. This is the approach to Thermodynamics based on the statistical-mechanical foundations provided by a Gibbs ensemble-like algorithm in nonequilibrium situations. The resulting nonequilibrium temperature-like variable - dubbed as quasitemperature - is shown to be a quantity measurable with appropriate "thermometric devices". A comparison of quasitemperatures that arise in different approximated nonequilibrium statistical-thermodynamic descriptions of the dissipative system is done. The validity of these different approximations is evaluated, and (in the framework of the theory) generalized Gibbs, Clausius, and Boltzmann's relations, as well as properties of the corresponding entropy-like function (or informational entropy in Jaynes-Shannon sense), that the theory introduces, are presented. Conceptual and physical aspects of the question are also discussed, and a partial comparison of these concepts with those arising in other approaches to irreversible thermodynamics is briefly attempted. This article is an enlargement of a paper in Fortschritte der Physik/Progress of Physics, 47, 9 (1999), where have been added extensive comments on the subject.
Considerations on nonequilibrium entropy and temperature
J. Galvão Ramos, Áurea R. Vasconcellos, and Roberto Luzzi
Grupo Mecânica Estatística de Sistema Dissipativos
Instituto de Física "Gleb Wataghin"
Universidade Estadual de Campinas
Cx. Postal 6165, 13083-970, Campinas, SP, Brazil
Received 4 April, 2000
Several aspects of the Thermodynamics of systems away from equilibrium are considered. Particular attention is given to the question of the concepts of entropy and temperature in arbitrary nonequilibrium conditions. Even though such state function and thermodynamic variable are elusive in such conditions, it is elaborated and discussed an approach to them that can be obtained in the framework of the so-called Informational Statistical Thermodynamics. This is the approach to Thermodynamics based on the statistical-mechanical foundations provided by a Gibbs ensemble-like algorithm in nonequilibrium situations. The resulting nonequilibrium temperature-like variable dubbed as quasitemperature is shown to be a quantity measurable with appropriate "thermometric devices". A comparison of quasitemperatures that arise in different approximated nonequilibrium statistical-thermodynamic descriptions of the dissipative system is done. The validity of these different approximations is evaluated, and (in the framework of the theory) generalized Gibbs, Clausius, and Boltzmann's relations, as well as properties of the corresponding entropy-like function (or informational entropy in Jaynes-Shannon sense), that the theory introduces, are presented. Conceptual and physical aspects of the question are also discussed, and a partial comparison of these concepts with those arising in other approaches to irreversible thermodynamics is briefly attempted. This article is an enlargement of a paper in Fortschritte der Physik/Progress of Physics,
47
, 9 (1999), where have been added extensive comments on the subject.
I Introduction
Nowadays, whereas the Thermodynamics of equilibrium states (or Thermostatics) is a very well established and successful discipline of long standing, the same cannot be said of the Thermodynamics of nonequilibrium states (or Irreversible Thermodynamics), although the latter has received a good deal of attention in recent decades, however permeated with lively controversy. Nonequilibrium Thermodynamics has associated quite difficult conceptual (and also practical) problems: Two fundamental ones are the definition of entropy and temperature out of equilibrium - if such concepts may have any meaning - along the evolution of irreversible processes in Nature, and the eventual setting of steady states in some cases.
This state function and this intensive variable have a precise definition in equilibrium states. Temperature is a perfectly measurable quantity in equilibrium states, and being measurable - that is, its value can be determined in an experiment (in the case of entropy indirect determination via calorimetric measurement is possible but of the difference of its values between an initial and a final equilibrium state) - we could say that it has physical meaning. Out of equilibrium the situation is not so clear cut and, except for particular situations that are peculiar or asymptotic cases. Meixner [1] has forcefully argued that a nonequilibrium entropy function is either not possible to define or several definitions are possible. This is the point of view we pursue, discuss, and illustrate in this paper, however presenting the idea that in a case by case analysis one may introduce, in a some way controlled approximation, a satisfactory state function that plays the role of a nonequilibrium entropy-like function, and let us call it quasientropy (In section IV we elaborate on the use of the prefix quasi, and on the levels of description of Thermodynamics). Consequently, there is not an absolute temperature out of equilibrium, but can be introduced a quantity (which becomes the reciprocal of the functional derivative of the quasientropy with respect to the energy of the subsystems of the open system) playing the role of a nonequilibrium temperature-like variable to be called - following already existing nomenclature in the physics of condensed matter - as quasitemperature.
According to the historical account of S.G. Brush [2] the concept of temperature preceeds the foundation of Thermodynamics as a well established science (It appears to go back to Galileo (c. 1592) who invented a thermoscope; Sanctorious (c. 1611) and J. Ray (c. 1632) developed an open capillar thermometer, and Duke Ferdinando II of Toscana (c. 1640) a one of close capillar; Sir Francis Bacon (c. 1640) advanced the idea that it is not temperature that is transmitted from hot to cold bodies). As known, the concept of absolute temperature in equilibrium is due to Lord Kelvin who set it on the universal thermodynamic basis provided by Carnot's theory. Outside the domain of equilibrium states, concepts akin to a nonequilibrium temperature have been introduced, on phenomenological basis and for particular subsystems (partial sets of degrees of freedom) of a sample under given experimental conditions. This was done by several authors seemingly beginning with Lev Davydovich Landau more than half a century ago: They were given for plasma [3]; for electron or nuclear spins [4]; for molecules [5]; for electrons excited in strong electric fields [6]; for electrons in superconductors [7]; for photoexcited carriers (photoinjected itinerant electrons and holes in semiconductors) [8]; for photoexcited phonons [9]; etc. Also theoretically-oriented definitions of quantities playing the role of nonequilibrium temperatures were introduced in the context of existing phenomenological thermodynamic theories [10-15]; we return to these points in the final section where concluding remarks are presented.
Kinetic and statistical-mechanical theories have also dealt with these questions, as they should. As known the grandiose Gibbsian scheme for Statistical Mechanics provides well established microscopic foundations for Thermostatics. For nonequilibrium situations there nowadays exist tentatives to provide microscopic (statistical-mechanical) foundations to Irreversible Thermodynamics, and, therefore, within their scopes it is possible to look for approaches to the thermal physics of nonequilibrium dissipative macroscopic systems at the molecular level. One such approach to irreversible thermodynamics is founded on the Nonequilibrium Statistical Operator Method (NESOM), a rigorous, soundly based, concise and practical formalism, which is a large generalization of Gibbs' theory (It may be considered a Gibbs' ensemble algorithm for arbitrary nonequilibrium systems). NESOM had precursors in, among others, Kirkwood [16], Green [17], Zwanzig [18], and Mori [19]. A fundamental piece for the foundation of the method is the quite relevant concept consisting in the principle of correlation weakening and the accompanying hierarchy of relaxation times introduced by Bogoliubov [20]. Several approaches to the NESOM are available, some based on heuristic arguments, others on projection-operator techniques. However, all these approaches can be brought together under a unifying variational principle, as reviewed in reference [21]. Along this line of thought, the NESOM may be considered as being encompassed within the framework of Jaynes' Predictive Statistical Mechanics [22,23], which is based on the principles of Bayesian probability and scientific inference, together with a criterion for setting up probability distributions, namely the maximum entropy formalism (MaxEnt) [24]. MaxEnt-NESOM recovers as special asymptotic limiting cases equilibrium statistical mechanics and linear response theory [25], and therefore provides statistical-mechanical basis for thermostatics and classical (sometimes called linear or Onsagerian) irreversible thermodynamics, and classical hydrodynamics.
Clearly, it is then tempting to look for statistical foundations within the framework of the MaxEnt-NESOM for the irreversible thermodynamics of systems arbitrarily away from equilibrium. This seems to be possible when resorting to the MaxEnt-NESOM including nonlinearities in the basic variables consisting of conserved (or quasi-conserved) densities and their nonconserving fluxes of all orders, as well as nonlocality (space correlations) and retro-effects (time correlations in the form of a "fading" memory), leading to what can be referred to as Informational Statistical Thermodynamics (IST), also sometimes dubbed as Information-theoretic Thermodynamics. IST was pioneered by Hobson [26] after the publication of Jaynes' seminal papers [27] on the foundations of statistical mechanics based on information theory. A brief description and partial historical notes are given in reference [28], and Sieniutjcz and Salamon [29] summarize existing extremum-principle theories in nonequilibrium thermodynamics; see also references [30, 31].
We consider next, in the context of IST, the question of the definition of an entropy-like function and a temperature-like variable in arbitrary nonequilibrium conditions. For that purpose the paper is organized as follows: In next section we provide a very brief theoretical background, indicating the main aspects of the method and the points relevant to the analysis to follow in section III, where we present the definitions of the field of quasitemperatures in two different descriptions of the macroscopic state of the system, as well as a generalized Gibbs' relation and a generalized Clausius' expression for the change of quasientropy. The last section is devoted to a discussion of the results and concluding remarks.
II Theoretical background in brief
The Nonequilibrium Statistical Operator Method - in either its heuristic construction or the variational one referred to as MaxEnt - has been extensively described in several papers and books; see for example [21, 25, 32-41]. For the sake of completeness we present in this section a very brief review of this theory, which consists on the results and expressions which are to be used in Section III and thereof.
In MaxEnt-NESOM the nonequilibrium macroscopic state of the system is characterized in terms of a basic set of thermodynamic variables (macrovariables), which are the statistical averages of a corresponding set of dynamical quantities (micro-mechanical observables) taken in terms of a statistical operator provided by the formalism. The main gist behind this procedure is to eliminate all irrelevant information necessary to characterize the macrostate, and can be considered a far-reaching generalization of methods introduced by Zwanzig and Mori [18, 19], with details given elsewhere [21, 38]. The construction of the formalism, as already noticed, is strongly based on the fundamental Bogoliubov's procedure of contraction of description with the accompanying hierarchy of relaxation times [20], a question further discussed by Uhlenbeck [42], and illustrative examples in the case of a spin-lattice system and a highly excited photoinjected plasma in semiconductors are given in references [43] and [44] respectively. These ideas were largely implemented, systematized and extended by the Russian School, mainly, Zubarev [32-36] and Peletminskii [39, 45]. Two fundamental, and physically quite relevant, inicial steps are introduced: First, the separation of the Hamiltonian of the system into two parts, namely
where
o is called the "relevant" (or secular) part consisting of the kinetic energies of the subsystems and a part of the interactions, namely - following Bogoliubov's principle - those strong enough to have associated correlation effects with very short relaxation times, meaning those much smaller than the characteristic time scale of the experiment (typically the resolution time of the detecting apparatus), and possessing certain symmetry properties as described below. The other term,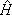 ¢, contains the interactions related to long-time relaxation mechanisms (that is, we emphasize, involving processes with relaxation times larger than the characteristic time scale of the experiment). Second, the required symmetry, referred to above, consist in what we call Zubarev-Peletminskii law, which is
¢, contains the interactions related to long-time relaxation mechanisms (that is, we emphasize, involving processes with relaxation times larger than the characteristic time scale of the experiment). Second, the required symmetry, referred to above, consist in what we call Zubarev-Peletminskii law, which is
where
j = 1, 2, ...,
n, the upper circumflex indicates mechanical quantities (Hermitian operators), the left side is the commutator of the basic dynamical variables {
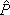
j} with
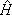
o, and the a's are - in an appropriate quantum representation -
c-numbers with dimension of frequency. However, may be the case, and this shall appear more clearly as we proceed in continuation, that quantities {
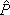
j} can be dependent on the space variable (i.e. when they are local densities) and then the quantities a may also depend on the space variable or be differential operators. It is worth noticing the case of the MaxEnt-NESOM generalized nonequilibrium grand-canonical ensemble, as described in [46, 47]: its construction requires introducing - as in the situation in equilibrium - the local densities of energy and of particles, say
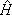
(

) and

(

). Application to them of the selection rule of Eq. (2) commands that the fluxes of energy and particles of all orders must be included as basic variables, as shown in Section III.
Steps (1) and (2) are of fundamental relevance to the formalism, and shall be better characterized as we proceed. At this point let us stress the quite important consequence that Eq. (2) provides a selection rule for the choice of the basic variables in a way to introduce a closure condition in the kinetic theory which provides the equations of evolution for the basic set of variables: This is the statistical-mechanical procedure that in MaxEnt-NESOM implements the so-called principle of equipresence of phenomenological irreversible thermodynamics (That is, if a quantity appears in the equations of evolution for the chosen set of basic variables, it ought to be incorporated as an additional variable in the thermodynamic state space) [29, 48]. In certain cases, for example the thermo-hydrodynamic-like one considered in this paper, the closure condition of Eq. (2) is not satisfied in a finite number of steps (that is for finite n), and, therefore, practical use of the formalism usually requires to introduce an appropriate truncation procedure at a certain level in the chain of operations in Eq. (2). This truncation implies in neglecting, that is, in considering as irrelevant the information for the problem in hands provided by a certain subset of basic variables. In other words, one introduces a truncated description of the macroscopic state of the system and, evidently, a justification of the approximation is required in each case. For this purpose one looks for a characterization of the approximation in terms of a characteristic expansion parameter, say an analog of the Knudsen number in Chapman-Enskog's kinetic theory, a question discussed elsewhere [49] with a particular case already considered in the second of references [31]: Suffice it to say that in space-dependent problems, as the one considered in this paper, consisting in a thermo-hydrodynamic in terms of the densities of particles and energy and their fluxes, a satisfactory parameter is lc/l, where l is each wavelength in the Fourier analysis (in the space coordinate) of the motion of the basic variables, and lc is a characteristic length of the system (typically an average velocity of propagation of the motion multiplied by a characteristic time). From this we can derive the intuitive criterion that when smoother and smoother in space the movement (the longer the wavelengths as compared to lc), the more and more contracted the description we can use (the shortest description - or stringest truncation - corresponds to the limit of traditional hydrodynamics). It may be noticed that this also implies, because of the existence of a frequency dispersion relation with low frequencies corresponding to the largest wavelengths, that, in general, there is a correspondence with a smoother and smoother in time movement, and then, summarizing, successive truncations are possible as the system approaches an increasingly quasi-uniform and quasi-static behavior. We return to this question in next section (see also Appendix I Appendix I. The Truncation Procedure ).
Once the representative set of basic variables has been chosen in the way described above, the nonequilibrium statistical operator is built in the MaxEnt-NESOM, and therefore in the context of Jaynes' Predictive Statistical Mechanics, using the principle of maximization of the informational-statistical entropy. This is done in the generalized way advanced by Zubarev and Kalashnikov [34] and revisited by us in [21], namely including retro-effects as a fading memory, what is attained through the inclusion of an ad hoc hypothesis which introduces from the outset irreversible evolution from an initial condition of preparation of the system: In this way the advanced solutions of Liouville equations are disregarded, and it is introduced a generalization of Kirkwood's time-smoothing formalism [16]. The procedure amount to incorporating into the formalism the concept of Bogoliubov's quasi-averages [50], which is a symmetry-breaking process that in this case corresponds to a breaking of the time-reversal symmetry in Liouville equation [21, 32-38]. We stress that the nonequilibrium statistical operator r(t) does satisfy Liouville equation, but, according to the formalism, irreversibility is introduceded in an ad hoc manner by disregarding the subset of advanced solutions from the whole set of solutions of Liouville equation, that is, those returning in time. This is accomplished by the fading-memory hypothesis (a particular Kirkwood-Zubarev time-smoothing procedure) amounting to a kind of generalized Stosszahlansatz.
The nonequilibrium statistical operator, r(t), thus obtained, is dependent (superoperator) on the basic set of dynamical quantities (mechanical observables) and a corresponding set of Lagrange multipliers (intensive nonequilibrium thermodynamic variables) that the variational procedure introduces. Moreover, a third relevant point is that r(t) can be split into two parts, namely
where  (t, 0) is an auxiliary distribution, or coarse-grained part of r(t), which provides the instantaneous macrostate of the system but does not account for the irreversible evolution of the system, what is taken care of by r¢(t): This partial term r¢ is the one that contributes to the production of informational entropy while
(t, 0) is an auxiliary distribution, or coarse-grained part of r(t), which provides the instantaneous macrostate of the system but does not account for the irreversible evolution of the system, what is taken care of by r¢(t): This partial term r¢ is the one that contributes to the production of informational entropy while  does not. A fourth important step in the theory consists in the construction of a nonlinear quantum kinetic theory, that is, the derivation of the equations of evolution for the basic variables, then providing a description of the evolution of the macroscopic state of the system. They are given by the average in terms of the MaxEnt-NESOM statistical operator of the corresponding Heisenberg's equations of motion, namely
does not. A fourth important step in the theory consists in the construction of a nonlinear quantum kinetic theory, that is, the derivation of the equations of evolution for the basic variables, then providing a description of the evolution of the macroscopic state of the system. They are given by the average in terms of the MaxEnt-NESOM statistical operator of the corresponding Heisenberg's equations of motion, namely
where triangular brackets stand for the statistical average
Using Eqs. (1) and (3), Eq. (4) can be rewritten as
where
Equation (6) is a far-reaching generalization of Mori's equations [21, 47], where J(0) is, in Mori's terminology, a precession term (or conserving term as better clarified later on) and J(1) is in most cases null because of the symmetry characteristics of the interactions in 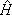 ¢ and the dependence of
¢ and the dependence of  (t, 0) on the basic variables. The last term
(t, 0) on the basic variables. The last term 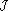 is a collision operator, the one contributing to the production of informational entropy. This collision operator has a formidable structure of unmanageable proportions, but it is possible to derive alternative expressions for it in terms of a series of partial collision operators, and a truncation of such series can be performed (in a certain order in the interaction strengths in
is a collision operator, the one contributing to the production of informational entropy. This collision operator has a formidable structure of unmanageable proportions, but it is possible to derive alternative expressions for it in terms of a series of partial collision operators, and a truncation of such series can be performed (in a certain order in the interaction strengths in 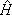 ¢) attaining a now mathematically practical approach [51]. This has been shown to be particularly successful in dealing with highly excited semiconductors probed in ultrafast laser spectroscopy experiments [52].
¢) attaining a now mathematically practical approach [51]. This has been shown to be particularly successful in dealing with highly excited semiconductors probed in ultrafast laser spectroscopy experiments [52].
We call the attention to the fact that quantities
j and Qj(t) = Tr{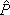 jr(t)} can be scalars, vectors, or tensors of any rank, the former even space dependent (densities of dynamical quantities), and the latter space and time dependent defining fields of thermodynamic variables. This is the case to be considered below. We noticed that - disregarding J(1) in Eq. (6) - the equations of evolution for the thermodynamics-field variables always take a general form as given by the expression [47]
jr(t)} can be scalars, vectors, or tensors of any rank, the former even space dependent (densities of dynamical quantities), and the latter space and time dependent defining fields of thermodynamic variables. This is the case to be considered below. We noticed that - disregarding J(1) in Eq. (6) - the equations of evolution for the thermodynamics-field variables always take a general form as given by the expression [47]
where r indicates tensor rank (r = 0 for scalar, r = 1 for vector, r ³ 2 for the usual tensors). In this Eq. (8), is present the divergence of the tensor of next rank to the one whose evolution is considered, which is the flux of the latter. The right hand side contains the collision operator 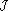 j, accounting for sources and sinks that may be present (that is, takes care of pumping and relaxation effects). We may noticed that for a null collision operator we do have the local conserving equation for the quantity Qj[r] (
j, accounting for sources and sinks that may be present (that is, takes care of pumping and relaxation effects). We may noticed that for a null collision operator we do have the local conserving equation for the quantity Qj[r] ( , t) .
, t) .
Finally, the connection with irreversible thermodynamics is done introducing a state function, a quasientropy in this case dubbed as informational entropy, given by the expression [21, 28, 31, 53],
that is, the average of minus the logarithm of the coarse-grained statistical operator. In this Eq. (8)  (t) is a time-dependent projection operator [21] - a generalization of those introduced by Zwanzig [18] and Mori [19] - whose role, implying in the increase of the informational entropy along the evolution of the system (or
(t) is a time-dependent projection operator [21] - a generalization of those introduced by Zwanzig [18] and Mori [19] - whose role, implying in the increase of the informational entropy along the evolution of the system (or 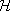 -like theorem), is discussed elsewhere [53]. The informational entropy production function is then
-like theorem), is discussed elsewhere [53]. The informational entropy production function is then
where the last equal sign is a result that, we recall, r(t) satisfies a Liouville equation with an infinitesimal source that goes to zero after the trace operation in the calculation of averages has been performed [21] (implying in only conserving the retarded solutions).
Equations (1) to (10) contain the main results that are of relevance for the analysis to be presented in next sections. As final words in this Section we notice that: (i) the nonlinear, nonlocal-in-space, and memory-dependent MaxEnt-NESOM transport equations [cf. Eqs. (4) to (7)] recover as particular asymptotic results (which follow further imposing quite restrictive conditions) Boltzmann's equation [37] and Mori's equations [21, 47]; (ii) In the framework of the MaxEnt-NESOM can be derived generalized forms for Glansdorff-Prigogine's thermodynamic evolution criterion and (in)stability criterion, as well as, in the strictly linear regime, a theorem of minimum production of quasientropy [54]; (iii) The MaxEnt-NESOM allows for the construction of a nonclassical thermo-hydrodynamic theory of large scope, which recovers as an asymptotic result classical hydrodynamics [55]; (iv) As already noticed, the formalism provides microscopic foundations to phenomenological irreversible thermodynamics [38, 53, 54], and the results of items (iii) and (iv) shall be partially used in the analysis that follows.
III On the question of quasi-thermodynamic variables
We turn now to the question of a nonequilibrium temperature-like variable in IST, or better to say to a field of nonequilibrium temperature (quasitemperature in the nomenclature we proposed) in the framework of a MaxEnt-NESOM thermo-hydrodynamics. Consider for simplicity a one-component gas of quasi-particles (for example carriers or phonons in condensed matter) in contact with a thermal reservoir, the latter at temperature To. For the choice of the representative set of basic variables we begin introducing the density of particles and the density of energy, the associated dynamical operators being indicated by  (
( ) and
) and 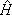 (
( ) (corresponding to the idea of introducing a nonequilibrium grand-canonical ensemble). According to the method, once the separation of the Hamiltonian as expressed by Eq. (1) has been performed, we proceed to incorporate additional basic variables - as enforced by the closure condition of Eq. (2) - calculating
) (corresponding to the idea of introducing a nonequilibrium grand-canonical ensemble). According to the method, once the separation of the Hamiltonian as expressed by Eq. (1) has been performed, we proceed to incorporate additional basic variables - as enforced by the closure condition of Eq. (2) - calculating
where  n(
n( ) and
) and  h(
h( ) (whose detailed expressions we omit for brevity; see [46, 47]) are interpreted as the dynamical quantities representing the flux of particles and of energy respectively, a result that follows from the work of Peletminskii and Sokolovskii [56] (see also in [33] Ch. IV, section 19.1). Hence, both fluxes are incorporated to the representative set of basic variables, and the next step in the chain that the procedure introduces leads to that
) (whose detailed expressions we omit for brevity; see [46, 47]) are interpreted as the dynamical quantities representing the flux of particles and of energy respectively, a result that follows from the work of Peletminskii and Sokolovskii [56] (see also in [33] Ch. IV, section 19.1). Hence, both fluxes are incorporated to the representative set of basic variables, and the next step in the chain that the procedure introduces leads to that
according to [56] and [46], where the right hand sides contain the divergence of second rank tensors that are the flux of the flux (or the second order flux) of particles and energy respectively. They are incorporated to the set of basic variables, the procedure of Eq. (2) is repeated, the divergences of third order fluxes arise on the right, and so on indefinitely. Consequently, in the present case the representative set of basic variables, enforced by the closure condition of Eq. (2), is composed of
where r = 2, 3, ... indicates the tensorial rank and order of the flux. Moreover, system and reservoir constitute an isolated system, and since the reservoir is considered to be ideal it needs be described only in terms of its Hamiltonian HR, and the statistical operator is then expressed as [57]
where rR is the canonical distribution in equilibrium of the reservoir with temperature To, and r(t) the system MaxEnt-NESOM statistical operator given by two terms as indicated in Eq. (3), and × stands for direct product. The auxiliary coarse-grained part of it is in this case given by
where, we recall, f (which plays the role of the logarithm of a nonequilibrium partition function) ensures the normalization of the distribution, and
are the corresponding Lagrange multipliers that the method introduces [21, 32-36, 45, 54]; dot stands as usual for scalar product and Ä for fully contracted product of tensors. Finally, the set of basic variables is designated by
where h( , t) = á
, t) = á (
( ) | tñ = Tr{
) | tñ = Tr{  (
( ) r(t) } , etc.
) r(t) } , etc.
The informational entropy is given by Eq. (9), and then in this case acquires the form
where we have defined the informational-entropy density,  (
( , t) (see [54]). This informational-entropy density satisfies a generalized Gibbs' relation given by
, t) (see [54]). This informational-entropy density satisfies a generalized Gibbs' relation given by
Furthermore, we call the attention to the important fact that the Lagrange multipliers (which constitute a set of intensive nonequilibrium thermodynamic variables also giving a complete description of the macrostate of the system as the basic set of specific variables of Eq. (17) does) are differential coefficients of the informational entropy, namely
where r = 2, 3, ...., and d stands for functional derivative [58]. These Eqs. (20) can be considered as nonequilibrium thermodynamic equations of state.
The informational entropy defined above, Eqs. (18) and (19), goes over the one in classical (linear or Onsagerian) thermodynamics, and to the one in equilibrium when the appropriate limits are taken ([53] and below); we recall that the description in terms of the dynamical variables of Eq. (13) amounts to a generalized nonequilibrium grand-canonical statistical operator, and when final equilibrium with the reservoir is achieved, one recovers the usual grand-canonical distribution in equilibrium [46, 47]. Taking this fact into account we redefine the MaxEnt-NESOM Lagrange multiplier associated with the energy density h( , t) as the reciprocal of a nonequilibrium space- and time-dependent temperature-like variable to be called, as noted, quasitemperature (or better to say a quasitemperature field), and denoted by Q(
, t) as the reciprocal of a nonequilibrium space- and time-dependent temperature-like variable to be called, as noted, quasitemperature (or better to say a quasitemperature field), and denoted by Q( , t), i.e.
, t), i.e.
where kB is Boltzmann constant. Moreover, for use in what follows, we introduce the definitions: (1) the mass density
where m is the mass of the particles in the system; (2) the drift velocity field
and (3) the quasiparticle internal energy field
Furthermore, in all the following analysis we will use - without loss of generality but in order to have a clearer picture of the physical ideas - a classical mechanical approach.
We next turn our attention to the consideration of the quasitemperature of Eq. (21), which as defined by Eq. (20a) is a functional of the energy density and particle density and the fluxes of all order of these densities [cf. Eq. (18)]. Let us consider now a couple of asymptotic (limiting) situations. This means truncated descriptions of the macroscopic state of the system consisting into neglecting in the statistical operator of Eq. (15) certain sets of terms involving higher order fluxes which are present in the exponential. We have already commented on the characterization of this approximation as implying to go over conditions involving ever smoother space and time dependence in the motion of mass and of energy. We consider this truncation procedure in the case of the photoinjected plasma in semiconductors in Appendix I Appendix I. The Truncation Procedure .
III.1 First truncated description: classical Fourier's heat diffusion
We consider first the case when we neglect all contributions in Eq. (14) except for the sets
for the macrovariables and the Lagrange multipliers respectively; for the latter subindex (1) means those given in this description, that is, in terms of only h, n, and 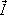 . Introducing the definition
. Introducing the definition
where 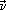 has dimensions of velocity, taking into account Eq. (22) and that a straightforward calculation in this first description results in that
has dimensions of velocity, taking into account Eq. (22) and that a straightforward calculation in this first description results in that
we arrive to the conclusion that in this description the velocity field of Eq. (26), related to the two Lagrange multipliers b(1) and 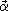 n(1), coincides with the drift velocity of Eq. (23), which is the one in classical hydrodynamics, that is
n(1), coincides with the drift velocity of Eq. (23), which is the one in classical hydrodynamics, that is 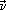 (1) (
(1) ( , t) =
, t) = 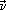 (
( , t) .
, t) .
Moreover, an also straightforward calculation in the classical limit to be consistently used in what follows, gives for the energy density the expression
But taking into account Eqs. (21)-(24) - however recalling that now Q is given in the truncated description of Eq. (25), and then we call it 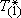 (
( , t) - together with Eqs. ( 27) and (28), it results a dependence of the quasitemperature in terms of the basic variables given by
, t) - together with Eqs. ( 27) and (28), it results a dependence of the quasitemperature in terms of the basic variables given by
where e is given by Eq. (24). But this expression is precisely the definition of the so-called kinetic temperature [59, 60], which coincides with the one given in classical irreversible thermodynamics. We stress that this quasitemperature (or kinetic temperature) is a functional of only the energy and particle (or mass) density.
We have subtitled this subsection as classical heat Fourier description, because when one writes the equations of evolution for the basic variables, the one for the energy density requires to be complemented in this truncated description by Fourier's constitutive equation for the energy flux leading to the parabolic Fourier diffusion equation for the thermal motion (cf. App. I).
III.2 Second truncated description: Telegraphist-like equation for the propagation of thermal motion
Consider now in Eq. (15) only the contributions arising out by keeping the sets
for the macrovariables and the Lagrange multipliers respectively; for the latter the subindex (2) means those given in this description, that is, they are functionals of h, n, 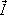 n, and
n, and 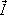 h . To clearly evidence the influence of the presence of the flux of energy
h . To clearly evidence the influence of the presence of the flux of energy 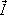 h (and the accompanying Lagrange multiplier
h (and the accompanying Lagrange multiplier 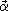 h ) in comparison with the first description of the previous subsection, we rewrite the auxiliary statistical operator in terms of a part, called
h ) in comparison with the first description of the previous subsection, we rewrite the auxiliary statistical operator in terms of a part, called  , depending on the terms carrying b, A, and
, depending on the terms carrying b, A, and 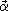 n, plus a second term, called Dr(2) , which carries all the dependence on the contribution
n, plus a second term, called Dr(2) , which carries all the dependence on the contribution 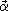 h ·
h ·  h (for details see App. II). Moreover, we introduce the definitions
h (for details see App. II). Moreover, we introduce the definitions
where we have introduced
etc., which are functionals of the Lagrange multipliers in the given representation. We call the attention to the fact that while ho is a functional of only b(2), A(2), and 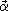 n(2), Dh is depending on them and also on
n(2), Dh is depending on them and also on 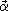 h(2). Because of Eqs. (32a) and (32d), the drift velocity of Eq. (27) can be written as
h(2). Because of Eqs. (32a) and (32d), the drift velocity of Eq. (27) can be written as
and then
where
with
(2)o depending only on b(2), A(2), and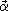 n(2), while D
n(2), while D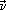 (2) depends on them and also on
(2) depends on them and also on 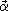 h(2) (going to zero when
h(2) (going to zero when 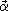 h(2) goes to zero). Finally, we introduce the quasitemperature in this second description, namely
h(2) goes to zero). Finally, we introduce the quasitemperature in this second description, namely
Making for simplicity the assumption that the term
h ·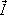 h included in the description used in this subsection, Eq.(30), produces small effects, we resort then to a calculation that keeps only the first order contribution in
h included in the description used in this subsection, Eq.(30), produces small effects, we resort then to a calculation that keeps only the first order contribution in 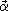 h in Dh, Dn, etc. Straightforward mathematical manipulations lead us to the following results:
h in Dh, Dn, etc. Straightforward mathematical manipulations lead us to the following results:
and
Taking into account that, as shown, in the first description (subsection III.1) the drift velocity
(1) and the quasitemperature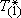 coincide with those of classical (linear or Onsagerian) thermo-hydrodynamics, we conclude that
coincide with those of classical (linear or Onsagerian) thermo-hydrodynamics, we conclude that 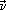 -
-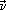 (2) 0 differs by a term proportional (in this linear approximation) to
(2) 0 differs by a term proportional (in this linear approximation) to 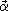 h, and the same is valid for the difference in quasitemperatures, namely, using Eqs. (29) and (39) we find that
h, and the same is valid for the difference in quasitemperatures, namely, using Eqs. (29) and (39) we find that
where Qk is the so-called kinetic temperature. Hence, while, we recall, the kinetic temperature - that is the quasitemperature in the strongly truncated first description of subsection III.1 - is only a functional of the densities of mass and of energy, the quasitemperature in the second description of this subsection III.2 is a functional, besides them, of the fluxes of mass and of energy (or, alternatively [cf. Eq. (38)] of the drift velocity and the Lagrange multiplier 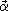 h).
h).
We have subtitled this subsection as "telegraphist-like equation for the propagation of thermal motion", because when one writes the equations of evolution for the basic variables, the one for the energy density and also the one for the mass density become hyperbolic-like equations (of the telegraphist type with sources) implying in damped undulatory motion. This kind of motion goes over to overdamped motion, and this one practically corresponds to the diffusive motion as resulting from Fourier law, as in the first description, in the limit of long wavelengths (cf. Appendix I Appendix I. The Truncation Procedure ). This is in accord with our previous statement that more and more contracted descriptions are possible as smoother and smoother in space and time is the movement. This particular transition is described elsewhere [61] for the specific case of the photoinjected nonequilibrated plasma in GaAs (see also Appendix I Appendix I. The Truncation Procedure ), and is also evidenced in an analysis in the framework of IST of experiments related to the techno-industrial process of thermal laser-stereolithography [62].
III.3 Measurement of a nonequilibrium temperature-like variable
We have described how one can define in IST a nonequilibrium temperature-like variable for a subsystem - the so-called quasitemperature - which, we stress, is the Lagrange multiplier that the method introduces, and which can be expressed as the reciprocal of the variational derivative of the MaxEnt-NESOM (informational) entropy with respect to the subsystem energy density. This is indicated in Eqs. (20) and Eq. (21). Thus, we emphasize once again, it is a functional of the complete set of basic variables that the closure condition (principle of equipresence) of Eq. (2) (see also Eqs. (11) et seq. in the present case) imposes. When it is introduced a truncation in the description, as done in subsections III.1 and III.2, we do have an approximated expression for such quasitemperature for the particular situations when to neglect higher order fluxes is acceptable (that is, the truncation criterion justifies this in the given experimental situation). In the description in terms of the stringent truncation described in subsection 3.1, one recovers the limit of classical (linear or Onsagerian) thermodynamics and the usual expression for the so-called kinetic temperature (the one in local equilibrium). Moreover, when the final global equilibrium (with the reservoirs) is attained, this quasitemperature Q, or those arising in any truncated description, say 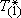 and
and  in previous subsections, go over the absolute temperature of equilibrium.
in previous subsections, go over the absolute temperature of equilibrium.
Clearly, a question to be decided is that of the measurement of these quasitemperatures. As noted, the quasitemperature is a thermodynamic variable in IST and then, together with the others, characterizes the nonequilibrium macrostate of the system that can be probed in the experiment. A description and interpretation of an experiment, we recall and emphasize, is irrevocably required to be done in the framework of a response function theory (that is, in terms of correlation functions [63] over, now in the situation being considered, the nonequilibrium ensemble). As shown elsewhere [21, 64] the MaxEnt-NESOM allows for the construction of a response function theory for systems arbitrarily away from equilibrium, which, differently to the case of experiments near equilibrium conditions, requires to be coupled to the set of equations of motion [cf. Eqs. (4) to (7)], i.e. those that arise out of the generalized nonlinear quantum kinetic theory that the method produces [21, 47, 51], which describes the irreversible evolution of the system. Moreover, besides the case of mechanical perturbations which can be expressed in terms of an interaction energy between system and the external source to be included in the Hamiltonian operator, within the MaxEnt-NESOM it is possible to develop a response function theory for thermal perturbations (the seventh of references [31]), which has been applied to the study of the photoinjected plasma in semiconductors [65]. The response function theory for mechanical perturbations in far-from-equilibrium systems was successfully used in the case of the photoinjected plasma in semiconductors under high levels of excitation, when optical and transport properties are observed in pump-probe experiments, and we can perform "thermometric measurements" of the quasitemperatures of the photoinjected carriers and also of the phonon modes. Using the very powerful and high-resolution experimental technique of ultrafast laser spectroscopy [66] it is possible to follow the ultrafast relaxation processes that develop in semiconductor and biological systems in the femtosecond (10-15 sec) time scale [52, 67, 68]. We illustrate the point in Fig. 1 which shows the evolution of the carrier quasitemperature in a pump-probe experiment on GaAs, when time-resolved luminescence spectra are obtained: the full line is the calculation in MaxEnt-NESOM [68] and the dots are from the experimental data [69], showing a very good agreement. Moreover, the influence of the presence in the representative set of basic variables of the energy flux has been analized in the case of photoinjected plasma in semiconductors in the presence of an electric field. The presence of intermediate to strong electric fields - what is common in semiconductor devices where a difference of a few volts provided by a simple pocket battery produces strong fields over small (nanometers) distances - creates strong electric currents (strong flux of carriers), which is accompanied, as a result of electro-thermal effects, of a relatively strong flux of energy. Therefore, the influence of the terms proportional to 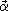 h in Eqs. (38) to (40) [which can also be expressed as proportional to a cross product of both fluxes, namely
h in Eqs. (38) to (40) [which can also be expressed as proportional to a cross product of both fluxes, namely 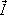 n(
n( , t) ·
, t) · 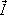 h(
h( , t) in Eqs. (39) and (40)] becomes relevant at fields beginning with a few kV/cm. The calculations in MaxEnt-NESOM [70] are corroborated by the analysis of the experimental data reported by Mendez et al. [71] obtained in experiments of modulation spectroscopy in semiconductor heterostructures. In fact, in this case one can determine the dependence of the quasitemperature with the electric field intensity, on the one hand from the experimental data as shown in Fig. 2 (right ordinate) and also on the basis of a calculation performed in the framework of MaxEnt-NESOM [70]. Furthermore, the difference between the quasitemperature including the presence of the flux of energy and the one excluding it, the latter being then the so-called kinetic temperature (or the local equilibrium temperature albeit the system is uniform), can be obtained. This is characterized by the function W, as described in [70] and shown in Fig. 2 (left ordinate): this function describes the difference between the quasitemperature in the presence of the energy flux and the kinetic (or local equilibrium) temperature. It indicates that in fact [cf. Eq. (40)] because of the presence of the energy flux the quasitemperature is larger than the one in the description that leads to the equivalent of classical thermodynamics. In Fig. 3 it is shown this difference in terms of the electric field, and the estimated values of the contribution to the energy flux that is proportional to the MaxEnt-NESOM Lagrange multiplier
, t) in Eqs. (39) and (40)] becomes relevant at fields beginning with a few kV/cm. The calculations in MaxEnt-NESOM [70] are corroborated by the analysis of the experimental data reported by Mendez et al. [71] obtained in experiments of modulation spectroscopy in semiconductor heterostructures. In fact, in this case one can determine the dependence of the quasitemperature with the electric field intensity, on the one hand from the experimental data as shown in Fig. 2 (right ordinate) and also on the basis of a calculation performed in the framework of MaxEnt-NESOM [70]. Furthermore, the difference between the quasitemperature including the presence of the flux of energy and the one excluding it, the latter being then the so-called kinetic temperature (or the local equilibrium temperature albeit the system is uniform), can be obtained. This is characterized by the function W, as described in [70] and shown in Fig. 2 (left ordinate): this function describes the difference between the quasitemperature in the presence of the energy flux and the kinetic (or local equilibrium) temperature. It indicates that in fact [cf. Eq. (40)] because of the presence of the energy flux the quasitemperature is larger than the one in the description that leads to the equivalent of classical thermodynamics. In Fig. 3 it is shown this difference in terms of the electric field, and the estimated values of the contribution to the energy flux that is proportional to the MaxEnt-NESOM Lagrange multiplier  [70].
[70].
Evolution of the carriers' quasitemperature in the photoinjected plasma in GaAs. Full line is a parameter-free calculation in MaxEnt-NESOM, and the dots are from the experimental data taken from reference [69] (After reference [68]). Reservoir temperature To is 300 K.
Therefore, we may say that the concept of quasitemperature in IST acquires physical meaning, in the sense that such quasi-thermodynamic variable can be characterized and measured experimentally. We stress that it is a functional of the whole set of macrovariables used for the description of the nonequilibrium (even arbitrarily far from equilibrium) thermodynamic state of the system, the one established by the selection rule of Eq. (2) in MaxEnt-NESOM, the counterpart of the principle of equipresence in phenomenological thermodynamic theories. The fact that such quasitemperatures may be calculated in truncated descriptions is a mere technical question of practical character: resorting to an appropriate criterion we can introduce approximations by neglecting unimportant contributions in a case by case analysis (see Appendix I Appendix I. The Truncation Procedure for an illustration).
We complement the illustrations with other examples. In the case of the experiments of Amand and Collet [72], it is shown in Fig. 4 the comparison of experimental data with the calculation - in the conditions of the experiment - in MaxEnt-NESOM of the evolution in time of the quasitemperature of the carriers [73]. Moreover, in this case is also reported data on the evolution of the carriers' concentration, which changes in time due to recombination effects and ambipolar diffusion out of the active volume of the sample: the experimental data and the calculation have good agreement as shown in Fig. 5.
As noticed, in the presence of electric fields the carriers produce a current and then the flux of carriers needs be introduced as a basic variable. In MaxEnt-NESOM the accompanying Lagrange multipliers can be interpreted as the drift velocity,
e(h) (t) , of electrons (e) and holes (h) divided by kBTc*(t) . The current of each type of carriers is proportional (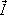 e(h) (t) = -(+) en(t)
e(h) (t) = -(+) en(t) 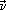 e(h)(t)) to this drift velocity. The drift velocity is derived in MaxEnt-NESOM and in Fig. 6 we show the evolution in time of the drift velocity of electrons in n-doped GaN [74] (in this case the carriers are only electrons). We can see the presence of an expected, so-called, velocity overshoot, that is, during the transient the velocity attains a value larger than the one in the steady state. Compounds of the III-Nitride type, as GaN, are nowadays of interest because of their use - as a result of being of wide gap - in laser and diodes working in the blue and near ultraviolet region of the electromagnetic spectrum. We do not present comparison with experimental values because the latter are not yet available. The dependence of the drift velocity in the steady state with the electric field strength is also calculated, and in Fig. 7 we show a comparison of our results in MaxEnt-NESOM with results of a calculation in a computer-modelling Monte Carlo approach [74]. However, in the case of GaAs the calculation can be compared with experimental results. This is shown in Fig. 8 for the so-called Ohmic domain (direct proportionality of current and electric field), which extends up to field intensity of roughly 2.5 kV/cm; beyond this point the results are not valid because of the intervalley scattering not accounted for in the model used in the calculation [75]. Furthermore, in the plasma in semiconductors, the energy in excess of equilibrium of the carriers, is being transferred to the lattice vibrations (mainly the optical phonons) which then become the so-called "hot phonons", that is having a quasitemperature larger than the reservoir temperature. In Fig. 9 we present the evolution of the quasitemperature in the case of a particular mode of longitudinal optical phonons in photoexcited GaAs. The calculation in MaxEnt-NESOM compares well with the experimental data (dots), and the so-called "hot phonon velocity overshoot" (during evolution the quasitemperature of some phonon modes becomes larger than the carriers' quasitemperature) is evidenced [76].
e(h)(t)) to this drift velocity. The drift velocity is derived in MaxEnt-NESOM and in Fig. 6 we show the evolution in time of the drift velocity of electrons in n-doped GaN [74] (in this case the carriers are only electrons). We can see the presence of an expected, so-called, velocity overshoot, that is, during the transient the velocity attains a value larger than the one in the steady state. Compounds of the III-Nitride type, as GaN, are nowadays of interest because of their use - as a result of being of wide gap - in laser and diodes working in the blue and near ultraviolet region of the electromagnetic spectrum. We do not present comparison with experimental values because the latter are not yet available. The dependence of the drift velocity in the steady state with the electric field strength is also calculated, and in Fig. 7 we show a comparison of our results in MaxEnt-NESOM with results of a calculation in a computer-modelling Monte Carlo approach [74]. However, in the case of GaAs the calculation can be compared with experimental results. This is shown in Fig. 8 for the so-called Ohmic domain (direct proportionality of current and electric field), which extends up to field intensity of roughly 2.5 kV/cm; beyond this point the results are not valid because of the intervalley scattering not accounted for in the model used in the calculation [75]. Furthermore, in the plasma in semiconductors, the energy in excess of equilibrium of the carriers, is being transferred to the lattice vibrations (mainly the optical phonons) which then become the so-called "hot phonons", that is having a quasitemperature larger than the reservoir temperature. In Fig. 9 we present the evolution of the quasitemperature in the case of a particular mode of longitudinal optical phonons in photoexcited GaAs. The calculation in MaxEnt-NESOM compares well with the experimental data (dots), and the so-called "hot phonon velocity overshoot" (during evolution the quasitemperature of some phonon modes becomes larger than the carriers' quasitemperature) is evidenced [76].
Evolution of the quasitemperature of carriers and of LO phonons for the mode indicated. Dots are experimental points derived from Raman scattering spectra. The so-called "hot phonon temperature overshoot" is evidenced. After [76].
III.4 Generalized Clausius' and Boltzmann's relations and a 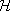 -theorem
-theorem
We close this section noticing that there exist a Clausius-like expression for the increase of the informational entropy in IST, resulting as a consequence of the modification of external constraints imposed on the system. In fact, consider the informational entropy of Eq. (18), and let us call ll (l = 1, 2, ..., s) a set of parameters that characterize the external constraints imposed on the system (one of them may be the volume, others external fields, etc.). Introducing infinitesimal modifications, say dll, the infinitesimal variation of informational entropy, as shown in the Appendix III Appendix III: Extremal Constraints and Informational Entropy , is given by
where dh, etc., are given by
The expressions for these nonexact differentials are (see Appendix IV Appendix IV: Additional Considerations on the Informational Entropy (or its Entropy or Quasientropy) ) the difference between the exact differential of each quantity (dh, dn, etc.) and
which are the average value of the change in the corresponding dynamical quantity due to the modification of the control parameters. The usual case of a change of volume starting with the equilibrium canonical distribution is presented as a simple illustration in Appendix IV Appendix IV: Additional Considerations on the Informational Entropy (or its Entropy or Quasientropy) . From Eq. (41) it is evident that the MaxEnt-NESOM Lagrange multipliers are integrating functions for the nonexact differentials. Let us now introduce the following redefinitions of the Lagrange parameters,
which, together with the use of Eq. (21) which defines the quasitemperature Q, allows us to write a space-dependent (in a infinitesimal region around point  ) Clausius-like expression for arbitrary nonequilibrium conditions, namely
) Clausius-like expression for arbitrary nonequilibrium conditions, namely
where we have introduced the rate of change of a nonexact differential for a generalized heat function, expressed by
In Eq. (45) is to be understood that the time integration extends in the time interval from to to t, along the trajectory of evolution of the nonequilibrium dissipative evolution of the system, where to is the initial time of preparation of the system and t the time a measurement is performed. As shown later on, cf. Eq. (61), the quantity in Eq. (45) integrated over the volume of the system is nonegative.
Moreover, using the redefinitions of Eqs. (44), we may noticed that the generalized Gibbs relation of Eq. (19) becomes
where on the left it has been evidenced the quasitemperature Q. In this Eq. (47), m plays the role of a quasi-chemical potential, 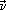 of a drift velocity, and
of a drift velocity, and  ,
, 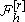 and
and 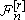 are, say, nonclassical nonequilibrium thermodynamic variables, playing the role of higher order drift velocities as discussed in [46, 47].
are, say, nonclassical nonequilibrium thermodynamic variables, playing the role of higher order drift velocities as discussed in [46, 47].
At this point, without going into details to be presented elsewhere [53], we comment on an interesting result. It consists in a kind of relation of the informational entropy in IST and Boltzmann's famous expression for the entropy in terms of the number of complexions at the microscopic mechanical level of description of the system, which are compatible with the macroscopic constraints. The nonequilibrium macroscopic constraints in IST are, we recall, the set of informational variables, for example the set of Eq. (17) which are the average values over the nonequilibrium ensemble of the mechanical quantities of Eq. (13) (we note again that this is the case of a generalized nonequilibrium grand-canonical-like ensemble). The informational (or IST) entropy is, as seen, a functional of these variables [cf. Eq. (19)], which in the thermodynamic limit satisfies that
where Q stands for all the variables in the set indicated in Eq. (17), and W is the number of complexions - phase space volume or number of quantum states (in classical and quantum mechanics respectively) - compatible with the imposed macroscopic constraints. The demonstration follows a similar line than the one used in equilibrium statistical mechanics.
Also, it is worth noticing that defining the quasi-entropy operator
whose average value with the statistical operator [cf. Eq. (9)] produces the IST entropy of Eq. (18), has the interesting property that, if  is the Liouville operator of the system, then [77]
is the Liouville operator of the system, then [77]
where
is the IST-entropy production of Eq. (10).
This result is a manifestation in the MaxEnt-NESOM-based IST, of the idea of complementarity between the microscopic and macroscopic levels of descriptions of many-body systems, as seemingly firstly considered by Niels Bohr [78], and elaborated by Rosenfeld [79] and Prigogine [80]; this topic is considered elsewhere [77]. The question of the diagonalization of the informational entropy operator, the analysis of its spectrum of eigenvalues, and some physical implications are given in the Ref. [81].
Finally, we notice that the informational entropy has associated a 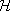 -theorem in Jancel's sense [82]. The informational entropy density
-theorem in Jancel's sense [82]. The informational entropy density  (
( , t) satisfies a continuity equation of the form [54]
, t) satisfies a continuity equation of the form [54]
where
s is the flux of informational entropy, namely
and the use of the definitions of Eqs. (44) and (22) allow us to introduce a generalized heat flux
q given by
Moreover, ss is the local in space informational-entropy production function, defined in Ref. [54], which is composed of two contributions, namely
where  is
is
with d defined in Eq. (19) and
defined in Eq. (19) and
The local in space informational-entropy prodution is composed of two terms, the first on the right of Eq. (56) is the one due to relaxation effects arising out of the interactions 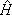 ¢ in Eq. (1) and contained in the contributions to the nonequilibrium statistical operator in Eq. (3), which, after the equations of evolution - Eqs. (4) to (7) - are used, can be expressed as
¢ in Eq. (1) and contained in the contributions to the nonequilibrium statistical operator in Eq. (3), which, after the equations of evolution - Eqs. (4) to (7) - are used, can be expressed as
where
h,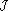 n, etc. are the collision operators of Eq. (7c) in the particular present case, that is, associated to the equations of evolution for the energy and particle densities and their vectorial and tensorial fluxes in the description of Eq. (17). We recall that J( 0) in Eq. (6) [the generalized Mori's precession term, and the one given rise to the divergence of the flux in Eq. (8)] does not contribute to the informational-entropy production
n, etc. are the collision operators of Eq. (7c) in the particular present case, that is, associated to the equations of evolution for the energy and particle densities and their vectorial and tensorial fluxes in the description of Eq. (17). We recall that J( 0) in Eq. (6) [the generalized Mori's precession term, and the one given rise to the divergence of the flux in Eq. (8)] does not contribute to the informational-entropy production  (see Ref. [54]). The second term on the right of Eq. (56) [cf. Eq. (58)] is a contribution in the form of products (scalar and tensorial) of fluxes and thermodynamic forces (the latter being the gradients of the Lagrange multipliers or intensive nonequilibrium thermodynamic variables), in a similar form to the one that appears in phenomenological thermodynamic theories. It should be noticed that after integration over space of the informational-entropy production density of Eq. (56) we obtain that
(see Ref. [54]). The second term on the right of Eq. (56) [cf. Eq. (58)] is a contribution in the form of products (scalar and tensorial) of fluxes and thermodynamic forces (the latter being the gradients of the Lagrange multipliers or intensive nonequilibrium thermodynamic variables), in a similar form to the one that appears in phenomenological thermodynamic theories. It should be noticed that after integration over space of the informational-entropy production density of Eq. (56) we obtain that
which is the bulk informational-entropy production, since the integral of sf vanishes (see Appendix IV Appendix IV: Additional Considerations on the Informational Entropy (or its Entropy or Quasientropy) ). This bulk informational-entropy production has associated what we have called a weak principle of non-negative informational entropy production [53, 54], namely
where, we recall, to stands for the initial time of preparation of the system in the given experiment and t is the time when a measurement is performed. It ought to be noticed that this theorem implies in an increase of the informational entropy along the evolution of the macroscopic state of the system as irreversible processes develop in the medium, starting at time to. But it does not tell us that the increase is monotonic, or more specifically, locally monotonic, a property imposed by some authors in other theories. However, it is conjecturable that this may be so - at least for the instantaneous bulk informational-entropy production - because along the evolution of the system it seems reasonable to expect a continuous loss of information. But this is not the case when a truncation is introduced (that is, the closure condition, imposed by Zubarev-Peletminskii selection rule of Eq. (2), is violated): during the irreversible evolution of the system at certain intervals the production of informational entropy may be negative [83], but, however, it is predominantly positive, so that the integral form of Eq. (61) is satisfied [84]. Fig. 10 provides a graphical description of this increase of informational entropy: We recall that the procedure involves the definition of a space of, what can be called, "relevant" (or informational) variables, that is, those chosen on the basis of the selection rule of Eq. (2). An "orthogonal" space is composed by the "irrelevant" variables, that is, those absent from the informational constraints in MaxEnt-NESOM [85]. The role of the time-dependent projection operator in Eq. (9) can now be better understood: It introduces a coarse-graining procedure implying that it projects the logarithm of the "fine-grained" statistical operator onto the subspace of the relevant (i.e. basic) variables, producing the logarithm of the "coarse-grained" statistical operator  (t, 0). We stress that the coarse-graining which follows by application of the projection procedure is time dependent, what is a result that the operation is dependent on the macroscopic state of the system at the time the projection is performed. The procedure eliminates the "irrelevant" variables, which are hidden in the statistical operator in the contribution r¢(t), since the time derivative present in its definition drives it outside the informational subspace. Topological and geometrical analyses of the question are provided by Balian et al. [85]. (See also Fig. 4). The result of Eq. (61) can be considered as a
(t, 0). We stress that the coarse-graining which follows by application of the projection procedure is time dependent, what is a result that the operation is dependent on the macroscopic state of the system at the time the projection is performed. The procedure eliminates the "irrelevant" variables, which are hidden in the statistical operator in the contribution r¢(t), since the time derivative present in its definition drives it outside the informational subspace. Topological and geometrical analyses of the question are provided by Balian et al. [85]. (See also Fig. 4). The result of Eq. (61) can be considered as a 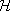 -theorem in Jancel's sense [82], and the increase in informational entropy is a result of the loss in information arising out of the chosen contracted description of the macrostate of the system (or incompleteness of information). At this point we do not claim any clear cut connection with the phenomenological second law of thermodynamics, and with Clausius' concept of uncompensated heat, except for the analogies [e.g. Eqs. (18), (19), (46), (48)], and the fact that in the proper asymptotic limit one recovers the well known and established results of local equilibrium and full equilibrium thermodynamics. Additional considerations on this topic are presented in Appendix IV
Appendix IV: Additional Considerations on the Informational Entropy (or its Entropy or Quasientropy)
.
-theorem in Jancel's sense [82], and the increase in informational entropy is a result of the loss in information arising out of the chosen contracted description of the macrostate of the system (or incompleteness of information). At this point we do not claim any clear cut connection with the phenomenological second law of thermodynamics, and with Clausius' concept of uncompensated heat, except for the analogies [e.g. Eqs. (18), (19), (46), (48)], and the fact that in the proper asymptotic limit one recovers the well known and established results of local equilibrium and full equilibrium thermodynamics. Additional considerations on this topic are presented in Appendix IV
Appendix IV: Additional Considerations on the Informational Entropy (or its Entropy or Quasientropy)
.
Graphical description of the Gibbs' and informational entropies depending on the MaxEnt-NESOM statistical operator. The projection - depending on the instantaneous state of the system - introduces a coarse-graining procedure consisting into projecting onto the subspace of the "relevant" variables associated to the informational constraints in MaxEnt-NESOM (cf. Eqs. (8) and (60); After reference [38]).
IV Discussion and concluding remarks
We have considered some general aspects of the thermodynamics of dissipative systems in conditions arbitrarily away from equilibrium; in this concluding section we further elaborate on the matter. On the previous sections particular attention was given to the question of entropy-like and temperature-like concepts in the nonequilibrium thermodynamics of dissipative systems. Concerning temperature out of equilibrium, we have already mentioned in the Introduction the use of nonequilibrium temperatures on phenomenological bases dating back apparently to a first proposal by Lev D. Landau more than half a century ago [3-9]. In the case of the classical irreversible thermodynamics no difficulty arises since it is postulated local equilibrium (as noted a reasonable approximation in the linear regime around equilibrium for quasi-static and quasi-uniform conditions). For arbitrarily away-from-equilibrium situations different concepts of nonequilibrium temperatures have been considered by several authors in several thermodynamic approaches. Meixner sets the concept of "dynamical temperature" [10]; Müller introduces "coldness" [11]; Muschik postulates a "contact temperature" [12]; Keizer introduces a nonequilibrium temperature in the framework of the postulation of a nonequilibrium thermodynamics based on statistical considerations of molecular fluctuations [13]; Nettleton considers the concept of a "kinetic temperature" related to the kinetic energy per particle [59]. Within the framework of Extended Irreversible Thermodynamics (EIT [86, 87]) it is defined a nonequilibrium temperature stemming as the partial derivative of a postulated nonequilibrium entropy-like function characteristic of EIT which incorporates the dissipative fluxes [88].
More recently, Garcia-Colin and Chan-Eu attempted to set a concept of an absolute nonequilibrium temperature strictly based on the zeroth law and the second law described in a Carnot-Clausius' framework [60]. In the process, a quasientropy is introduced, called calortropy, which possesses a differential form similar in appearance to the one in our Eq. (46) above, but where a local equilibrium temperature and a momentum expansion, the latter expressed in terms of a complete set of tensor Hermite polynomials are present instead of the tensorial fluxes of all orders in Eq. (43). According to these authors, in the proposed decomposition of a Carnot cycle into an infinite number of infinitesimal Carnot cycles, the temperature of the working substance undergoing an irreversible process characteristic of the infinitesimal Carnot cycle of interest is necessarily the same as the temperature of one of the heat reservoirs, and must be regarded as the local temperature of the body in question [60]. Viewed in this way the heat reservoir of the infinitesimal cycle in question may double as a thermometer in the absolute temperature scale that indicates the temperature value T: The body undergoes an irreversible process and T is the thermodynamic temperature of the infinitesimal body as well as the heat reservoir - a thermometer [60, 89]. It seems to us that, on the one hand, this implies that local equilibrium has been achieved and thus a restriction is introducing loosing generality; and on the other, in general conditions, as pointed out by Jaynes [90], T denotes the temperature of a heat bath with which the system is momentarily in contact and this may or may not be the temperature of the system [emphasis is ours]. Moreover, Carnot's principle (in its original form) describes only the net result of a process that begins and ends in thermal equilibrium; it does not permit us to draw any such conclusion as dS/dt ³ 0 at intermediate times: Indeed entropy has been defined only for equilibrium states, in which there is no time dependence. The calortropy function cannot be directly measured but is to be determined in terms of the local temperature and the other variables in the thermodynamic state space (energy, the Hermite polynomials, etc.), and therefore, one needs to obtain and solve the constitutive equations for those variables. The calortropy is considered as representing a filing cabinet containing information on the physical properties of the macroscopic system of interest, made up on a careful analysis of the system properties via constitutive equations [60, 89]. It is worth noticing that the idea closely resembles what is done in the case of IST in terms of the informational entropy. Finally, the authors of reference [60] conclude that there is no other temperature admissible than that by the zeroth law and the second law, the quantity which is associated with the heat reservoirs, even when the system is away from equilibrium, and that, when this notion of temperature does not hold valid, the extended theory of irreversible processes as known of in the literature is no longer applicable and one whould pass from the realm of irreversible thermodynamics governed by the thermodynamic laws into a nonthermodynamic realm of many-body phenomena as yet uncharted [60].
These considerations seem to arise out of a particularly chosen level of description, as shall be discussed later on. First some comments. The considerations of Chan-Eu and Garcia-Colin (let us call the theory Orthodox Irreversible Thermodynamics - OIT for short) are also present in, at least, two other theories, namely EIT and IST. In both the functions corresponding to the calortropy of OIT are the quasientropies, which are functionals of the basic set of variables in the chosen thermodynamic state space. In EIT the quasientropy is postulated, and it is constructed on symmetry considerations in terms of invariant terms involving the densities of energy and of particles, and their first vectorial fluxes, but all higher order vectorial fluxes can also be introduced [91]. The equations of evolution for the basic variables (densities and fluxes) are derived, and, in principle, once solved the proposed quasientropy can be calculated, if desired. The basic difference with OIT resides in the definition of the differential coefficients of the EIT quasientropy: The fundamental one is the variational derivative of the quasientropy with respect to the energy density, taken as the definition of a nonequilibrium temperature in EIT, and which is the local equilibrium temperature of classical (linear) irreversible thermodynamics, and of OIT, plus terms depending on the fluxes. Moreover, of course, there are differences in the other differential coefficients, as well in their interpretation, mainly in what concerns to those related to the fluxes in EIT [92], or in OIT those related to the tensor Hermite polynomials.
Let us now consider IST. The mechano-statistical approach provides a description with a foundation at the molecular (microscopic) level. As discussed elsewhere [93] the statistical approach in MaxEnt-NESOM briefly described in Section II, contains the main requeriments in phenomenological theory: the principle of equipresence (to which we have referred to previously), the principle of objectivity (that is invariance under Galilean transformation), and memory effects (which maybe can also be referred to as historicity). The first one is accounted for, as already noticed, by the selection rule imposed by Zubarev-Peletminskii law [cf. Eq. (2)]. Therefore, as we have seen in previous sections, the nonequilibrium thermodynamic state space in IST is composed of the average values of mechanically defined quantities which we have called the "relevant" or informational variables. As shown, in IST a quasientropy is defined, the so-called informational entropy (in Jaynes-Shannon's sense [23, 94]) as given by Eq. (9). It is a functional of the representative set of basic variables [cf. Eqs. (17) to (19)], and then its differential coefficients - which are the MaxEnt-NESOM Lagrange multipliers - are functionals of the basic variables that define the nonequilibrium thermodynamic state space in IST [cf. Eqs. (20) and (21)]. One particular difference with OIT is that the functional derivatives of the informational entropy in IST is with respect to the average values of mechanical quantities that have precise physical meaning, while in OIT is with respect to the tensor Hermite polynomials not directly related to observables. The fundamental difference is in what concerns the variational derivative of the calortropy in OIT and of the informational entropy in IST with the energy. In the first case there appears the reciprocal of the local equilibrium temperature (the one in IST in the truncated description described in subsection III.1), while in the second is a generalized nonequilibrium temperature [cf. Eqs. (20a) and (21)] dubbed as quasitemperature. This nonequilibrium temperature-like variable in IST goes over, as already noticed, to the local equilibrium temperature (in the limit of quasi-static and quasi-uniform hydrodynamic motion; the case dealt with in subsection III.1), and to the absolute temperature when global equilibrium is achieved. Same arguments apply to the case of the Lagrange multiplier associated to the density of particles, which can be interpreted as a quasi-chemical potential divided by the quasitemperature [cf. Eqs. (44a)]; the other Lagrange multipliers,
h, n,
n, 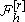 ,
, 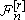 [cf. Eqs. (44b) to (43f)] go to zero in the asymptotic limit when global equilibrium is achieved. Moreover, as shown [cf. Eq. (61)] there follows a weak principle of non-negative informational entropy production (graphically described in Fig. 10). This, in principle, resides in the coarse-graining condition imposed by the use of the time-dependent projector in Eq. (9) (see Fig. 10) implying in the use of a subspace (the so-called informational space) of the whole space of dynamical variables: the result of Eq. (61), which as noticed is a kind of
[cf. Eqs. (44b) to (43f)] go to zero in the asymptotic limit when global equilibrium is achieved. Moreover, as shown [cf. Eq. (61)] there follows a weak principle of non-negative informational entropy production (graphically described in Fig. 10). This, in principle, resides in the coarse-graining condition imposed by the use of the time-dependent projector in Eq. (9) (see Fig. 10) implying in the use of a subspace (the so-called informational space) of the whole space of dynamical variables: the result of Eq. (61), which as noticed is a kind of  -theorem in Jancel's sense [82], was also obtained along a different, albeit apparently equivalent, approach by del Rio and Garcia-Colin [95], who have interpreted it as characterizing the fact that every time the system is observed, information is lost (what, in our approach, is realized by the projection of the fine-grained Gibbs entropy on the given informational space as depicted in Fig. 10). Again we stress that this does not imply in a direct connection with the second law. Furthermore, it does not imply in a monotonic increase of the entropy-production function, but in a permanent increase of its integration along the trajectory of evolution, starting at to, of the state of the system in the given thermodynamic informational space, as indicated by Eq. (61). It is conjecturable that the production of informational entropy is in fact monotonically increasing in time, since it cannot be perceived how information can be gained in some partial time intervals. However, this may only be true when the selection rule [Zubarev-Peletminskii law of Eq. (2)] for the choice of the representative set of basic variables is satisfied. The monotonic increase of
-theorem in Jancel's sense [82], was also obtained along a different, albeit apparently equivalent, approach by del Rio and Garcia-Colin [95], who have interpreted it as characterizing the fact that every time the system is observed, information is lost (what, in our approach, is realized by the projection of the fine-grained Gibbs entropy on the given informational space as depicted in Fig. 10). Again we stress that this does not imply in a direct connection with the second law. Furthermore, it does not imply in a monotonic increase of the entropy-production function, but in a permanent increase of its integration along the trajectory of evolution, starting at to, of the state of the system in the given thermodynamic informational space, as indicated by Eq. (61). It is conjecturable that the production of informational entropy is in fact monotonically increasing in time, since it cannot be perceived how information can be gained in some partial time intervals. However, this may only be true when the selection rule [Zubarev-Peletminskii law of Eq. (2)] for the choice of the representative set of basic variables is satisfied. The monotonic increase of  (t) may be lost when a truncation of the representation is performed, but ameliorated as more and more higher order fluxes are incorporated into the description [83, 84, 49]. The informational-entropy production also satisfies, as already mentioned, generalized forms of Glansdorff-Prigogine thermodynamic criterion for evolution and (in)stability criterion for systems arbitrarily away from equilibrium and governed by nonlinear kinetic laws, as well as a theorem of minimum informational entropy production in the strictly linear regime around equilibrium [54].
(t) may be lost when a truncation of the representation is performed, but ameliorated as more and more higher order fluxes are incorporated into the description [83, 84, 49]. The informational-entropy production also satisfies, as already mentioned, generalized forms of Glansdorff-Prigogine thermodynamic criterion for evolution and (in)stability criterion for systems arbitrarily away from equilibrium and governed by nonlinear kinetic laws, as well as a theorem of minimum informational entropy production in the strictly linear regime around equilibrium [54].
An important point to emphasize is that the informational entropy  (t) of Eq. (18) also follows from the maximization of its expression as given by Eq. (9) subject to the normalization of the coarse-grained statistical operator
(t) of Eq. (18) also follows from the maximization of its expression as given by Eq. (9) subject to the normalization of the coarse-grained statistical operator  (t,0) and the constraints consisting in to give the average values of the basic variables (the densities, vectorial fluxes, and all order tensorial fluxes) at the given time t only. The auxiliary distribution
(t,0) and the constraints consisting in to give the average values of the basic variables (the densities, vectorial fluxes, and all order tensorial fluxes) at the given time t only. The auxiliary distribution  (t,0) provides the so-called instantaneously "frozen" quasi-equilibrium distribution - we recall that the irreversible evolution of the system is described by r¢ in Eq. (3) -, producing at each time the same average values for the basic variables as does r(t). This is quite in accord with Meixner's statement that "one is so much accustomed to the concept of a nonequilibrium entropy that one would like to retain it as a quantity of physical significance. This is indeed possible on a higher level of description in which the state at time t is not characterized by the histories of the external variables up to time t, but instead by these external variables and by a set of internal variables, all of them being taken at the same time t. The resulting theory is essentially the classical thermodynamics of irreversible processes and its entropy is the well-defined entropy of frozen equilibrium which is a function of the independent external and of the internal variables. It is a different matter whether in a given material the internal variables can always be properly identified with molecular processes" [1]. Therefore, the informational entropy in IST satisfies these requirements and, moreover, the, in Meixner's nomenclature, internal variables are identified with molecular processes, that is, as already noticed, they are the average values over the nonequilibrium ensemble of well defined mechanical quantities. On the other hand, the fine-grained (or Gibbs) entropy, we recall, contains the retro-effects - going back to the initial time to of preparation of the sample -, but in the form of a fading memory [present in r¢(t) of Eq. (3)] and is conserved (see Fig. 10). Moreover, and the equations of evolution for the representative set of basic variables, that the associated kinetic theory produces [cf. Eqs. (4) to (7)], are memory-dependent, and besides, as noticed, nonlocal in space, nonlinear, and encompassing irreversibility, the latter property characterized by the
(t,0) provides the so-called instantaneously "frozen" quasi-equilibrium distribution - we recall that the irreversible evolution of the system is described by r¢ in Eq. (3) -, producing at each time the same average values for the basic variables as does r(t). This is quite in accord with Meixner's statement that "one is so much accustomed to the concept of a nonequilibrium entropy that one would like to retain it as a quantity of physical significance. This is indeed possible on a higher level of description in which the state at time t is not characterized by the histories of the external variables up to time t, but instead by these external variables and by a set of internal variables, all of them being taken at the same time t. The resulting theory is essentially the classical thermodynamics of irreversible processes and its entropy is the well-defined entropy of frozen equilibrium which is a function of the independent external and of the internal variables. It is a different matter whether in a given material the internal variables can always be properly identified with molecular processes" [1]. Therefore, the informational entropy in IST satisfies these requirements and, moreover, the, in Meixner's nomenclature, internal variables are identified with molecular processes, that is, as already noticed, they are the average values over the nonequilibrium ensemble of well defined mechanical quantities. On the other hand, the fine-grained (or Gibbs) entropy, we recall, contains the retro-effects - going back to the initial time to of preparation of the sample -, but in the form of a fading memory [present in r¢(t) of Eq. (3)] and is conserved (see Fig. 10). Moreover, and the equations of evolution for the representative set of basic variables, that the associated kinetic theory produces [cf. Eqs. (4) to (7)], are memory-dependent, and besides, as noticed, nonlocal in space, nonlinear, and encompassing irreversibility, the latter property characterized by the 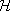 -theorem-like result of Eq. (61). In that way we may say that IST, which right now is having a robust development, arises as a quite promissing approach to irreversible thermodynamics. These results are partially illustrated elsewhere [96], in a study of a nonequilibrated fermion system in interaction with a system of bosons, and in contact with an external heat reservoir. This system grossly represents a n-doped semiconductor, with the interaction of the electrons with the phonons represented by a deformation potential interaction.
-theorem-like result of Eq. (61). In that way we may say that IST, which right now is having a robust development, arises as a quite promissing approach to irreversible thermodynamics. These results are partially illustrated elsewhere [96], in a study of a nonequilibrated fermion system in interaction with a system of bosons, and in contact with an external heat reservoir. This system grossly represents a n-doped semiconductor, with the interaction of the electrons with the phonons represented by a deformation potential interaction.
An important observation needs be stressed at this point: The informational entropy, and consequently also its production, is defined in terms of the basic variables and therefore it is mathematically obtained from Eq. (18) once the equations of evolution (for given initial and boundary conditions) for the basic variables have been solved, and the Lagrange multipliers (which include the quasitemperature Q and f or logarithm of the nonequilibrium partition function) have been obtained. Therefore, we stress, the quasitemperature, quasi-chemical potentials, and all the other Lagrange multipliers are obtained from appropriate equations of evolution (for example, see Eq. (59) in reference [21], and also particular applications in semiconductor physics in reference [97]), and after that, as noticed, the informational entropy can be calculated. A careful and detailed description in the case of the photoinjected plasma in semiconductors will be reported in a future article [98]. Furthermore, hydrodynamic and transport properties of the photoinjected plasma in semiconductors, based on IST, are reported elsewhere [99-102].
Consequently, and as already stated in the Introduction, it is presently available a powerful, concise, and soundly based statistical formalism for the description of systems arbitrarily away from equilibrium where strong dissipative processes are in action - the so-called MaxEnt-NESOM -, which provides, as shown, the foundations for IST. As noticed, of the different approaches to MaxEnt-NESOM , the one due to D.N. Zubarev (recently deceased [103]) appears as a physically sound as well as elegant method of quite practical application. We recall that IST involves a thermodynamics that is nonlinear, nonlocal in space (incorporates space correlations), and including fading memory (incorporates dampened correlations in time, that is decaying retroeffects). It also provides microscopic foundations to EIT, which is recovered under particularly restrictive conditions (the limit of weak nonlinearity, absence of space and time correlations, etc.). Moreover, in IST the transport coefficients and other correlation functions are not open or adjustable quantities, but are given at the microscopic mechano-statistical level, that is, derived from the many-body quantum or classical mechanics averaged over the nonequilibrium ensemble characterized by the MaxEnt-NESOM statistical distribution [46, 47]. In that way we do have a theory in the realm of many-body physics, showing at present a satisfactory degree of development, and which was initiated in the decade of the fifties by Jaynes and Hobson, and presenting a quite promising future.
Concerning the already noticed point that there apparently exists controversy - or maybe better to say confusion - on the approach to the construction of a thermodynamics for irreversible processes outside the Onsagerian domain [10-15, 26, 29, 30, 31, 53, 59, 60, 86, 91, 93, 95, 104, 106], such situation, we think, arises out of the kind of level of description to be chosen. It is considered [107] that there exist four levels of description of Thermodynamics:
(i) The one based on the two fundamental laws of thermodynamics and the rules of operation of the Carnot cycles. This is sometimes referred to as the engineering point of view or CK Thermodynamics (for Clausius and Kelvin).
(ii) The mathematical approach, as the one based on differential geometry instead of Carnot cycles, sometimes referred to as CB Thermodynamics (for Caratheodory and Born).
(iii) The axiomatic point of view, replacing Carnot cycles and differential geometry by a set of basic axioms, that try to encompass the previous ones and extend them, or TC Thermodynamics (for Tisza and Callen).
(iv) The statistical-mechanical point of view, based of course on the substrate provided by the microscopic mechanics (at a molecular, or atomic, or particle level) plus theory of probability, which can be referred to as Gibbsian Thermodynamics or Statistical Thermodynamics.
It is not an easy task to readily classify all attempts within this scheme, but we can try that for the three specially mentioned in the text. The approach of Chan-Eu and Garcia-Colin [60, 89] belongs to level (i), and for that reason we have called their theory as Orthodox Irreversible Thermodynamics; EIT belongs to level (iii) that is, being based on a set of plausible axioms; and IST is clearly within the scope of level (iv). Moreover, it may be considered that Truesdell's Rational Thermodynamics [106] belongs to the level (ii), being built on the inclusion of thermodynamic-like concepts in the mechanics of continuum media. IST, belonging to level (iv), is associated to the statistical-mechanical approach which is considered to be by itself richer, and the point of departure of a whole array of generalizations [107].
In what concerns IST, since it is based on the MaxEnt-NESOM and Jaynes' Predictive Statistical Mechanics, it has also associated the controversies that accompany this statistical approach, as for example analyzed by Dougherty [108]. One in particular is the one that opposes Jaynes' School and the Brussels' School [104], but we side with Dougherty's point of view that the controversy may be void since the differences may not exist or be partial, with both approaches having common or at least partially overlapping domains of validity [109]. It may be noticed that the nonequilibrium statistical ensemble formalism is considered to have by far the most appealing structure, and be a most effective method for dealing with nonlinear transport equations [108].
In a final statement we restate our previous manifestation that we follow J. Meixner [1, 10] lead in that state functions and state variables which have well defined meaning and foundations in the case of Thermostatics, are unlikley to surface under such clear cut outlook in the case of nonequilibrium dissipative systems. Different approaches along different levels of description are possible, as noted above, with each one to be evaluated under its own merits [107]. We have here attempted a partial contribution to the subject, emphasizing the merits of IST, namely, (1) determination at the microscopic (statistical-mechanical) level of transport coefficients; (2) derivation of the nonlocal-in-space, retro-effects-dependent, and highly nonlinear equations of evolution for the basic macrovariables as nonequilibrium averages over the MaxEnt-NESOM ensemble of the mechanical equations of motion of the many-body system; (3) construction of a nonclassical nonlinear thermo-hydrodynamics of an apparently large scope; (4) and the quite important fact of a connection with a response function theory for far-from-equilibrium systems. However, we restate the important point in what refers to the second law, noticed at the end of Section 3, in that we do not claim any clear cut connection with the phenomenological second law of thermodynamics, and with Clausius' concept of uncompensated heat, except for the analogies [e.g. Eqs. (18), (19), (46), (48)], and the fact that in the proper asymptotic limit one recovers the well known and established results of local equilibrium and full equilibrium thermodynamics. Additional considerations on this topic are presented in Appendix IV Appendix IV: Additional Considerations on the Informational Entropy (or its Entropy or Quasientropy) . Response function thory allows for the fundamental step of establishing the connection of theory and experiment, and then permiting to obtain measurements of the quantities that the theory introduces, hence given them physical meaning. Those quantities that play a role similar to the ones defined in local equilibrium and global equilibrium (to whose values tend in that limits) like temperature, chemical potential, and pressure, we have called them in IST as quasitemperature, quasi-chemical potential, and quasipressure. We recall that according to the Webster Dictionary, " quasi, adj. 1: having some resemblance (as in function, effect or status) to a given thing: seeming, virtual - often joined to second element with a hyphen". Since they are the differential coefficients of a function of state, which in equilibrium is the entropy of the system, such function may be dubbed as quasientropy (informational entropy in IST). Once again we stress that the quasi-thermodynamic variables in IST are related to the experiment via the MaxEnt-NESOM response function theory, and then can be measured: Figs 1 and 2 present a couple of examples relative to the quasitemperature and Fig. 11 illustrates the case of determination of the quasi-chemical potential from the gain spectrum of platelets of CdS (dots are experimental points and the full curve is the calculation in MaxEnt-NESOM) [110].
The gain spectra in platelets of CdS. The experimental conditions are indicated in the inset, where it is also indicated the value of the quasitemperature of the carrier system, and the arrow indicate the position of the quasi-chemical potential (After reference [105]).
We conclude pointing out that, as we wrote before, in the present paper we did not make any attempt to work the difficult task of describing and comparing different approaches to irreversible thermodynamics, or even classify them into the program of four levels referred to above. We have concentrated the attention only in the case of OIT at the, say, orthodox level, EIT at the axiomatic level, and IST at the statistical-mechanical level. We have emphasized the latter calling the attention to the fact that it appears to have a broad scope, allows for practical calculations based on a substrate provide by the dynamics of many-particle physics, and the quite relevant fact that associated - in a consistent way - with a response function theory allows for a connection with the experimental realm: different properties of dissipative systems can be calculated and compared with the experimental data thus validating the theory and providing verification and corroboration of, among other things, the quasitemperature and quasi-chemical potentials that IST defines, as shown in some of the figures presented.
Acknowledgments
We acknowledge the support provided to our Group at different opportunities by the São Paulo State Research Foundation (FAPESP), the National Research Council (CNPq), the Ministry of Planning (Finep), UNICAMP Foundation for Teaching and Research (FAEP), IBM-Brasil, the USA-National Science Foundation (US-Latin America Cooperation, Washington, USA); and the John Simon Guggenheim Memorial Foundation (New York, USA). Useful and enlightening discussions with L.S. Garcia-Colin (UAM, Mexico) and J. Casas-Vázquez and D. Jou (UAB, Barcelona) are gratefully acknowledged. One of us (RL) greatly appreciates the kind and warm hospitality received during his stays at the Physics Department of the UAB, where the first draft of this paper was prepared.
In the main text we have noticed that the closure condition of Eq. (2) (or Zubarev-Peletminskii law for a closure in the choice of the quasi-conserved variables in Mori's sense, and which implies in a statistical-mechanical condition which have a clear relation to the principle of equipresence in phenomenological thermodynamic theories) requires, when inhomogeneous processes are present, to incorporate the fluxes of energy and matter of all orders. Truncation procedures are then necessary for, in general, an accessible mathematical handling of the problem, and, evidently, such approximation needs be evaluated in each case. In other words, a criterion needs be devised allowing to assert that the information retained in the description is, for the purposes of the analysis of the problem at hands, the relevant one and the rest can be neglected (that is to say - in practical terms in the way used in section III - that one may use in the statistical operator the dynamical quantities densities and their fluxes up to a certain order r, accompanied by the corresponding Lagrange multipliers, and neglecting the terms with order larger than r). Such criterion can be devised, and is reported in Ref. [49]. We have noticed in section II that it implies, in words, that when smoother and smoother the space and time variation of the densities of matter and of energy, the shorter the description needed. We have also pointed to the fact that a quantifying parameter is the ratio  /l, where l is the shorter wavelength involved and lc a quantity with the dimension of length of the order of the average velocity of propagation of the motion multiplied by a characteristic time, related to the relaxation times for the space and time correlations of the involved quantities to die down.
/l, where l is the shorter wavelength involved and lc a quantity with the dimension of length of the order of the average velocity of propagation of the motion multiplied by a characteristic time, related to the relaxation times for the space and time correlations of the involved quantities to die down.
For illustration we briefly summarized here a particular case, namely the hydrodynamic behavior of the carrier system in the photoinjected plasma in semiconductors (second and last of references [31]). First we evaluated the frequency dispersion relation for plasma waves in several truncated descriptions, and the results were compared with the exact one (a well known result that can be found in the literature on the theory of many-electrons, which is the equivalent to solving - what is possible in this case - the description involving the infinite fluxes). The group velocity in the frequency dispersion relation is determined and compare with the one in the exact result for different ranges of wavelength. It is shown that to obtain the correct result up to the square in the wavenumber (square on the reciprocal of the wavelength) one needs to introduce fluxes up to order r = 4. The control parameter is in this case g = (vtpl/l)2, where tpl is the plasma wave period at infinite wavelength, and v the average velocity of propagation of the plasma waves.
The equations of evolution for the plasma and second sound for such system have been derived in what we call IST of zero rank, IST(0) (when only the densities are introduced as basic variables) and IST of first rank, IST(1) (when we introduce the densities and their first (vectorial) fluxes) [100]. Consider second sound: without going into details which are given in [100], in IST(1) the equation of evolution for the energy density is
where ch is the velocity of propagation and Dh the thermal diffusivity, and we have neglected on the right sources that are dependent on the space variation of the energy flux and which are small in the range of wavelength being considered. Eq. (I.1) is a hyperbolic-type equation known as the telegraphist equation, which also appears in the domain of phenomenological extended irreversible thermodynamics. From Eq. (I.1) we can derive the frequency dispersion relation for second sound, solution of the characteristic equation
where Q is the wavenumber. Solution of Eq. (I.2), namely,
tells us that, depending on the wavenumber and the macroscopic state of the system which determines the values of ch and Dh (in the case considered they are dependent on the carrier quasitemperature), the propagation of the second sound acquires the form of a damped undulatory motion for values of wavelength l < chqh (where qh is the energy relaxation time given by qh = 2Dh/ , and therefore dependent on the carrier quasitemperature), or simple diffusive movement for l > chqh, which is the region corresponding to overdamped motion. In the latter region the motion is well described by the solution of Fourier diffusion equation of classical irreversible thermodynamics
, and therefore dependent on the carrier quasitemperature), or simple diffusive movement for l > chqh, which is the region corresponding to overdamped motion. In the latter region the motion is well described by the solution of Fourier diffusion equation of classical irreversible thermodynamics
Hence, clearly, there exists, as indicated, a control parameter, which in this case of second sound propagation is  /l with
/l with  = chqh = 2Dh/ch, such that, we restate, for l >
= chqh = 2Dh/ch, such that, we restate, for l >  second sound propagation can be well described in IST(0), corresponding to classical (Onsagerian) irreversible thermodynamics (and when diffusive motion predominates), and for l <
second sound propagation can be well described in IST(0), corresponding to classical (Onsagerian) irreversible thermodynamics (and when diffusive motion predominates), and for l <  one needs to introduce IST(1), providing in this case results similar to those of phenomenological extended irreversible thermodynamics. In Fig. 12 it is shown, as a function of the carrier quasitemperature, the energy-relaxation time (see right ordinate), and the critical curve that separates the domains of IST(0) and IST(1). A way to experimentally corroborate these results is, for example, Raman scattering, with the expected Raman spectra shown in Fig. 13: Three spectra are drawn corresponding to the conditions indicated by cross points in Fig. 12, going from weakly damped, to strongly damped, to overdamped movement. In the first case one should expect a doublet of Brillouin lines with linewidth
one needs to introduce IST(1), providing in this case results similar to those of phenomenological extended irreversible thermodynamics. In Fig. 12 it is shown, as a function of the carrier quasitemperature, the energy-relaxation time (see right ordinate), and the critical curve that separates the domains of IST(0) and IST(1). A way to experimentally corroborate these results is, for example, Raman scattering, with the expected Raman spectra shown in Fig. 13: Three spectra are drawn corresponding to the conditions indicated by cross points in Fig. 12, going from weakly damped, to strongly damped, to overdamped movement. In the first case one should expect a doublet of Brillouin lines with linewidth  ; in the second case the bands are shifted with respect to those in the first case and very broad; and finally in the third case the Brillouin-doublet colapses in a unique shiftless band (the so-called Rayleigh band), with a bandwidth related to the diffusivity and the square of the wavenumber (when multiplied by Planck constant the wavenumber is the momentum transfer in the scattering event, and the frequency shift is the transferred energy). Closing this Appendix, it is worth noticing that if we consider T* = 400 K, then the energy relaxation time is nearly 1 ps, and the wavelength at the boundary of the domain of validity of IST(0) is nearly 1.3 × 10-4 cm; moreover, it may be noticed that since the carrier concentration is nearly 1.4 × 1017 cm3, the average spacing between carriers is of the order of 2 × 10-6 cm.
; in the second case the bands are shifted with respect to those in the first case and very broad; and finally in the third case the Brillouin-doublet colapses in a unique shiftless band (the so-called Rayleigh band), with a bandwidth related to the diffusivity and the square of the wavenumber (when multiplied by Planck constant the wavenumber is the momentum transfer in the scattering event, and the frequency shift is the transferred energy). Closing this Appendix, it is worth noticing that if we consider T* = 400 K, then the energy relaxation time is nearly 1 ps, and the wavelength at the boundary of the domain of validity of IST(0) is nearly 1.3 × 10-4 cm; moreover, it may be noticed that since the carrier concentration is nearly 1.4 × 1017 cm3, the average spacing between carriers is of the order of 2 × 10-6 cm.
The energy-relaxation time (right ordinate) for a range of values of the carrier quasitemperature. The full line separates the regions of values of the wavenumber (left ordinate), the one on the lower right being the domain of validity of classical irreversible thermodynamics. Outside this region one needs to resort to extended forms of thermodynamics (in the present case are informational statistical thermodynamics of rank zero and one respectively). The numerical parameters used are those of GaAs, and the carrier concentration is n = 1.4 × 1017 cm-3 (After reference [95]).
A description of the Raman spectra for the three situations indicated by cross points in Fig. 12: T* = 100 K - upper full lines; T* = 200 K - lower full lines; T* = 300 K - dashed lines (After reference [95]).
Appendix II. Energy-flux Contribution to the Statistical Operator
In the second truncated description of subsection III.2, Eq. (31) gives the corresponding basic sets of macrovariables and Lagrange multipliers. On the basis of that, the auxiliary statistical operator is
This statistical operator can be rewritten as
where
and, evidently,
According to Heims-Jaynes perturbation expansion for averages [111], the average value of a quantity  can be written as
can be written as
where the first term on the right is the average with the partial auxiliary operator
that is, a quantity independent of  of Eq. (II.4), and DM is an infinite series of terms which are correlation-like functions of operator
of Eq. (II.4), and DM is an infinite series of terms which are correlation-like functions of operator  and increasing powers in operator
and increasing powers in operator  (what consequently implies a series in powers of the Lagrange multiplier
(what consequently implies a series in powers of the Lagrange multiplier 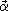 ), and DM goes to zero when
), and DM goes to zero when  (i.e.
(i.e. 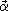 ) goes to zero.
) goes to zero.
To first order in  (which implies cases when one can expect weak contributions from the term containing the flux of energy), we find that
(which implies cases when one can expect weak contributions from the term containing the flux of energy), we find that
with
and 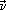 (
( , t) and h(
, t) and h( , t) are given in Eqs. (38) and (39) respectively. Moreover,
, t) are given in Eqs. (38) and (39) respectively. Moreover,
and
Finally, completing these details, one finds that the Lagrange multipliers
n (associated to the flux of mass) in both descriptions are related by the expression,
From the knowledge of the generating functional f(t) in Eq. (18), which is related to a kind of quasi-thermodynamic potential, we can derive by simply differentiating it with respect to the variables on which it depends, namely the Lagrange multipliers in MaxEnt-NESOM, the average values of the basic dynamical variables, that is
etc.
where, we recall, d stands for functional derivative [58]. Because of Eqs. (III.1) there follows the generalized Gibbs relation of Eq. (19). But the system also depends on external parameters, call them l1, l2, ..., ls, and let us consider the modifications introduced by very small variations of these external constraints, say dl1, ¼ , dls. Such parameters may be, say, the volume, external fields, etc.
Let us look on the variation of the informational entropy as a consequence of introducing the variations dlj (j = 1,, 2, ¼, s). We have
where, for simplicity we omitted to write the  - and t-dependence of all the quantities and the dots stand for all the other contributions involving the particle density n and all the fluxes of both densitites. But
- and t-dependence of all the quantities and the dots stand for all the other contributions involving the particle density n and all the fluxes of both densitites. But
and then
where
etc. , with
etc., and, we recall,
for any dynamical variable. Therefore, as already stated in the main text, the non-exact differentials of Eq. (III.4) are the difference between the differential of the macrovariable and the average value of the variation of the corresponding dynamical variable, as a consequence of the change in the external parameters. Let us take a simple case for illustration, namely a system in equilibrium described by the canonical distribution, and let us perform an infinitesimal variation dV in the volume. Then
and, according to the results above,
where
once we take into account that p = - á¶H/¶Vñ eq. = -¶U/¶V is the pressure and U the internal energy, U = á 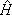 ñeq. Hence,
ñeq. Hence,
which is a particular well known form of the first law, with
q and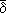 w being the nonexact differentials associated to changes in heat and work.
w being the nonexact differentials associated to changes in heat and work.
According to the results described in subsection III.4,
But, at this point we can introduce in this Eq. (IV.1) the result of Eq. (III.5) in Appendix III Appendix III: Extremal Constraints and Informational Entropy , and then, after some algebra it follows that
where
Eq.(IV.2) is a expression, in principle, quite difficult to calculate along this line (which of course is not practical at all). But before going into the practical one, we can derive some simple general considerations: First we notice that, as the informational entropy is the average of the operator  (t, 0) of Eq. (50), the production of informational entropy is the average of the operator
(t, 0) of Eq. (50), the production of informational entropy is the average of the operator  (t, 0) = d
(t, 0) = d (t, 0)/dt =
(t, 0)/dt =  [
[ (t, 0),
(t, 0), 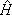 ]; second, if the latter is null, that is, the informational entropy operator is conserved, no dissipation follows and r¢ in Eq. (3) is null (this reinforces the fact already stated that relaxation processes are contained in this contribution to the statistical operator, while the coarse-grained part does not contain dissipative effects); third, Eq. (IV.2), once the integral equation for the operator is solved via the iterative process, becomes composed of an infinite series of terms involving correlations of all orders in the production-of-informational-entropy operator; this allows to classify the dissipative processes in first, second, etc., orders. To illustrate the matter, let us take the lowest (first) order, and also assume that the contribution in Eq. (IV.2) arising out of the contribution in De is much smaller than the one from the constant, i.e. 1, term, and then
]; second, if the latter is null, that is, the informational entropy operator is conserved, no dissipation follows and r¢ in Eq. (3) is null (this reinforces the fact already stated that relaxation processes are contained in this contribution to the statistical operator, while the coarse-grained part does not contain dissipative effects); third, Eq. (IV.2), once the integral equation for the operator is solved via the iterative process, becomes composed of an infinite series of terms involving correlations of all orders in the production-of-informational-entropy operator; this allows to classify the dissipative processes in first, second, etc., orders. To illustrate the matter, let us take the lowest (first) order, and also assume that the contribution in Eq. (IV.2) arising out of the contribution in De is much smaller than the one from the constant, i.e. 1, term, and then
Taking into account the case we have been considering, that is, as described by the statistical operator of Eq. (15), after some algebraic manipulations we find that Eq. (IV.4) becomes
But, instead of the time derivatives we can introduce the corresponding equations of motion, and then
Integrating by parts in the space coordinate the contribution containing the divergence of the flux and taking into account that the fluxes vanish on the system boundaries, we find that
a non-negative quantity as shown in [53-54, 100].
Moreover, we recall, the space and time-dependent informational-entropy production is the one of Eq. (52), composed of a contribution that involves the known form of a product of thermodynamic forces and fluxes plus a term involving the collision operators 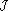 . Eq.(IV.7), we stress once again, is the approximate expression for the increase of the informational entropy in the lowest order in the relaxation effects.
. Eq.(IV.7), we stress once again, is the approximate expression for the increase of the informational entropy in the lowest order in the relaxation effects.
The informational-entropy production of Eq. (56), we recall, satisfies generalized forms of Glansdorff-Prigogine's evolution and (in)stability criteria, as well as, in the strictly linear regime, a generalized form of Prigogine's theorem of minimum entropy production (the informational one in the present case), results that are an immediate consequence of the principle of maximization of informational entropy, as demonstrated in reference [54].
References
[1] J. Meixner, "Thermodynamics of irreversible processes has many faces", in Irreversible Aspects of Continuum Mechanics, edited by H. Parkus and L. I. Sedov (Springer, Wien, 1968); Rheol. Acta 12, 465 (1973); see also reference [10] below.
[2] S. G. Brush, The Kind of Motion We Call Heat (North Holland, Amsterdam, 1976).
[3] L. D. Landau, Zh. Eksp. Teor. Fiz.7, 203 (1937); A. A. Dougal and L. Goldstein, Phys. Rev. 109, 615 (1958).
[4] H. B. G. Casimir and F. K. du Pre, Physica 5, 507 (1938); also A. Abragam, The Principles of Nuclear Magnetism (Oxford Univ. Press, Oxford, 1961).
[5] C. S. Wang-Chang, G. E. Uhlenbeck, and J. de Boer, in Studies of Statistical Mechanics, Vol. 2, edited by J. de Boer and G. E. Uhlenbeck (North Holland, Amsterdam, 1964).
[6] H. Fröhlich, Proc. Roy. Soc. (London) 188A, 521 (1947).
[7] V. A. Shklovskii, Fiz. Tver. Tela 17, 3076 (1975) [Soviet Phys. Solid State 17, 2040 (1976)].
[8] J. Shah and R. C. C. Leite, , Phys. Rev. Lett. 22, 1304 (1969).
[9] J. Shah, R. C. C. Leite, and J. F. Scott, Solid State Commun. 8, 1089 (1970).
[10] J. Meixner, in Foundations of Continuum Thermodynamics, edited by J. J. Domingos, M. N. Nina, and J. H. Whitelaw, (McMilland, London, 1974).
[11] I. Müller, Arch. Ration. Mech. Anal. 40, 1 (1971).
[12] W. Muschik, Arch. Ration. Mech. Anal. 66, 379 (1977); J. Non-Equilib. Thermodyn. 4, 277 (1979).
[13] J. Keizer, J. Chem. Phys. 65, 4431 (1976); ibid. 69, 2609 (1978); ibid. 82, 2751 (1985); also, Statistical Thermodynamics of Nonequilibrium Processes (Springer, New York, 1987).
[14] J. Casas-Vázquez and D. Jou, J. Phys. A: Math. Gen. 14, 1221 (1981); D. Jou and J. Casas-Vázquez, Phys. Rev. A 45, 8371 (1992); J. Casas-Vázquez and D. Jou, Phys. Rev. E 49, 1040 (1994).
[15] D. Jou, J. Casas-Vázquez, and G. Lebon, Rep. Prog. Phys. 51, 1105 (1988); Contemporary Phys. 33, 411 (1992).
[16] J. G. Kirkwood, J. Chem. Phys. 14, 180 (1946); ibid. 15, 72 (1947).
[17] M. S. Green, J. Chem. Phys. 20 , 1281 (1952); ibid. 22, 398 (1954).
[18] R. Zwanzig, in Lectures in Theoretical Physics, Vol. 3, edited by W. E. Brittin, B. W. Downs, and J. Downs, (Wiley-Interscience, New York, 1961).
[19] H. Mori, , Prog. Theor. Phys. (Japan) 33, 423 (1965).
[20] N. N. Bogoliubov, in Studies in Statistical Mechanics I, edited by J. de Boer and G. E. Uhlenbeck (North Holland, Amsterdam, 1962), see also reference [50].
[21] R. Luzzi and A. R. Vasconcellos, Fortschr. Phys./ Prog. Phys. 38, 887 (1990).
[22] E. T. Jaynes, "Predictive Statistical Physics" in Frontiers of Nonequilibrium Statistical Physics, edited by J. T. Moore and M. O. Scully, (Plenum, New York, 1986).
[23] E. T. Jaynes, reprinted articles and notes in E.T. Jaynes' Papers on Probability, Statistics, and Statistical Physics, edited by D. Rosenkrantz (Reidel, Dordrecht, 1983).
[24] E. T. Jaynes, and papers by other authors in, The Maximum Entropy Formalism, edited by R.D. Levine and M. Tribus (MIT Press, Cambridge, MA, 1978).
[25] W. T. Grandy, Foundations of Statistical Mechanics, Vol. I: Equilibrium Theory and Vol. II: Nonequilibrium Phenomena (Reidel, Dordrecht 1987 and 1988 respectively); also Phys. Rep.62, 175 (1980).
[26] A. Hobson, J. Chem. Phys. 45, 1352 (1966); Am. J. Phys. 34, 411 (1966).
[27] E. T. Jaynes, Phys. Rev. 106, 620 (1957); ibid. 108, 171 (1957).
[28] L. S. Garcia-Colin, A. R. Vasconcellos, and R. Luzzi, J. Non-Equilib. Thermodyn. 19, 23 (1994); R. Luzzi, A. R. Vasconcellos, and J. G. Ramos, Fortsch. Phys./Prog. Phys., 47, 401 (1999); R. Luzzi, A. R. Vasconcellos, and J. G. Ramos, Statistical Foundations of Irreversible Thermodynamics, Texte zur Physik Series, edited by W. Ebeling, (Teubner Verlag, Leipizig, 2000).
[29] S. Sieniutjcz and P. Salamon, introductory lecture in Advances in Thermodynamics, Vol. 3: Nonequilibrium Theory and Extremum Principles, edited by S. Sieniutjcz and P. Salamon (Taylor and Francis, New York, 1990).
[30] R. E. Nettleton and S. L. Sobolev, J. Non-Equilib. Thermodyn. 20, 205 (1995).
[31] A. R. Vasconcellos, R. Luzzi, and L. S. Garcia-Colin, (1) Phys. Rev. A 43, 6622 (1991); (2) ibid. A 43, 6633 (1991); (3) J. Non-Equilib. Thermodyn. 20, 103 (1995); (4) ibid. 20, 119 (1995); (5) J. Mod. Phys. B 9, 1933 (1995); (6) ibid. 9, 1945 (1995); (7) Physica A 221, 478 (1995); (8) ibid. 221, 495 (1995).
[32] D. N. Zubarev and M.Yu. Novikov, Fortschr. Phys./Prog. Phys. 21, 703 (1973).
[33] D. N. Zubarev, Neravnovesnaia Statisticheskaya Termodinamika (Izd. Nauka, Moscow, 1971) [English Transl.: Nonequilibrium Statistical Thermodynamics (Consultants Bureau, New York, 1974), Ch. IV.
[34] D. N. Zubarev and V. P. Kalashnikov, Teor. Mat. Fiz. 1, 137 (1969) [Theor. Math. Phys. (USSR) 1, 108 (1970)].
[35] D. N. Zubarev, in Reviews of Science and Technology: Modern Problems in Mathematics, Vol. 15 (in Russian), edited by R. B. Gamkreludze (Izd. Nauka, Moscow, 1980) [English Transl. Soviet Math. 16, 1509 (1991)].
[36] D. N. Zubarev, V. Morosov, and G. Röpke, Statistical Mechanics of Nonequilibrium Processess, Vol. 1: Basic Concepts, Kinetic Theory and Vol. 2: Relaxation and Hydrodynamic Processes (Akademie Verlag, Berlin, 1996 and 1997 respectively).
[37] J. G. Ramos, A. R. Vasconcellos, and R. Luzzi, Fortschr. Phys./Prog. Phys., 43, 265 (1995).
[38] R. Luzzi, A. R. Vasconcellos, and J. G. Ramos, Foundations of a Nonequilibrium Ensemble Formalism, Fundamental Theories of Physics Series, van der Merwe, A., Ed. (Kluwer Academic, Dordrecht), book of future publication.
[39] A. I. Akhiezer and S. V. Peletminskii, Methods of Statistical Physics (Pergamon, Oxford, 1981).
[40] J. A. McLennan, Introduction to Nonequilibrium Statistical Mechanics (Prentice-Hall, Englewoods Cliffs, 1989).
[41] H. Mori, I. Oppenheim, and J. Ross, in Studies in Statistical Mecanics I, edited by J. de Boer and G. E. Uhlenbeck (North Holland, Amsterdam, 1962)..
[42] G. E. Uhlenbeck, in Studies in Statistical Mechanics I, edited by M. Kac (Am. Math. Soc., Providence, RI, 1963).
[43] L. L. Buishvili and M. D. Sviadadze, Physica 59, 697 (1972).
[44] A. R. Vasconcellos, A. C. Algarte, and R. Luzzi, Physica A 166, 517 (1990); R. Luzzi, A. R. Vasconcellos, and J. G. Ramos, Ukrainian Journal of Physics, in press.
[45] S. V. Peletminskii and A. A. Yatsenko, Zh. Ekps. Teor. Fiz. 53, 1327 (1967) [Soviet Phys. JETP 26, 773 (1968)].
[46] J. R. Madureira, A. R. Vasconcellos, and R. Luzzi, J. Chem. Phys. 109, 2099 (1998).
[47] J. R. Madureira, A. R. Vasconcellos, R. Luzzi, J. Casas-Vázquez, and D. Jou, J. Chem. Phys. 108, 7568 (1998); ibid. 108, 7580 (1998).
[48] C. Truesdell and R.A. Toupin, "The classical field theories", in Encyclopaedia of Physics, Vol. III/1, edited by S. Flügge (Springer, Berlin 1960).
[49] J. G. Ramos, A. R. Vasconcellos, and R. Luzzi, "A truncation criterion in Informational Statistical Thermodynamics", J. Chem. Phys., 112, 2692 (2000).
[50] D. N. Bogoliubov, Lectures in Quantum Statistics II (Gordon and Breach, New York, 1970).
[51] L. Lauck, A. R. Vasconcellos, and R. Luzzi, Physica A 168, 789 (1990); J. R. Madureira, A. R. Vasconcellos, R. Luzzi, and L. Lauck, Phys. Rev. E, 57, 3637 (1998).
[52] See for example the review article: A. C. Algarte, A. R. Vasconcellos, and R.Luzzi, Phys. Stat. Sol. (b) 173, 487 (1992).
[53] R. Luzzi, A. R. Vasconcellos, and J. G. Ramos, "Statistical Irreversible Thermodynamics in a Nonequilibrium Ensemble Formalism", Rivista del Nuovo Cimento, submitted.
[54] M. A. Tenan, A. R. Vasconcellos, and R. Luzzi, Fortschr. Phys./Prog. Phys., 47, 1 (1996).
[55] J. G. Ramos, A. R. Vasconcellos, and L. S. Garcia-Colin, Braz. J. Phys., 27, 585 (1997).
[56] V. P. Peletminskii and A. I. Sokolovskii, Theor. Mat. Phys. (USSR) 18, 85 (1974); see also [73].
[57] J. Seke, Phys. Rev. A 21, 2156 (1980).
[58] R. Courant and D. Hilbert, Methods of Theoretical Physics (Willey-Interscience, New York, 1953).
[59] R. E. Nettleton, Can. J. Phys. 72, 106 (1994).
[60] B. C. Eu and L. S. Garcia-Colin, "Irreversible Processes and Temperature", preprint (we thank the authors for kindly forwarding us a first version of their paper); and Phys. Rev. E 54, 2501 (1996).
[61] A. R. Vasconcellos, R. Luzzi, D. Jou, and J. Casas-Vázquez, Physica A 212, 369 (1994); see also the last of references [31].
[62] R. Luzzi, M. F. Scarparo, J. G. Ramos, A. R. Vasconcellos, M. Barros, and A. Kiel, J. Non-Equilib. Thermodyn., 22, 197 (1997).
[63] P. C. Martin, "Measurements and Correlation Functions", in Many-Body Physics, edited by C.de Witt and R. Balian (Gordon and Breach, New York, 1968); R. Luzzi, Tópicos em Termodinâmica Estatística de Processos Dissipativos: Teoria da Função Resposta (Edunicamp, Campinas, 2000).
[64] R. Luzzi and A. R. Vasconcellos, J. Stat. Phys. 23, 539 (1980).
[65] A. R. Vasconcellos, R. Luzzi, and A. S. Esperidião, Phys. Rev. B 52, 5021 (1995); A.R. Vasconcellos, R. Luzzi, D. Jou, and J. Casas-Vázquez, Phys. Rev. B 52, 5030 (1995).
[66] For example, see R. R. Alfano, in New Techniques and Ideas in Quantum Measurement Theory, edited by D. M. Greenberg, Annals of the NYAS Vol. 480 (New York Acad. Sci., New York, 1986).
[67] R. Luzzi and A. R. Vasconcellos, in Semiconductors Probed by Ultrafast Laser Spectroscopy, Vol. 1, edited by R. R. Alfano (Academic, New York, 1984).
[68] A. C. Algarte, A. R. Vasconcellos, and R. Luzzi, Braz. J. Phys., 26, 543 (1996).
[69] R. J. Seymour, M. R. Junnakar, and R. R. Alfano, Solid State Commun. 41, 657 (1982).
[70] A. R. Vasconcellos, R. Luzzi, J. Casas-Vázquez, and D. Jou, Physica A, 234, 699 (1996).
[71] E. E. Mendez, F. Agulló-Rueda, and J. M. Hong, Phys. Rev. Lett. 60, 2426 (1988).
[72] T. Amand and J. Collet, J. Phys. Chem. Solids, 46, 1053 (1985).
[73] A. C. Algarte, A. R. Vasconcellos, and R. Luzzi, Phys. Stat. Sol. (b), 173, 487 (1992).
[74] C. G. Rodrigues, A. R. Vasconcellos, V. N. Freire, and R. Luzzi, Appl. Phys. Lett., submitted.
[75] C. G. Rodrigues, A. R. Vasconcellos, V. N. Freire, and R. Luzzi, Phys. Rev. B, submitted.
[76] A. C. Algarte, A. R. Vasconcellos, and R. Luzzi, Phys. Rev. B, 54, 11311 (1996).
[77] R. Luzzi, J. G. Ramos, and A. R. Vasconcellos, Phys. Rev. E., 57, 244 (1998).
[78] N. Bohr, Dialectica 2, 312 (1948).
[79] L. Rosenfeld, in Proc. Int. School "Enrico Fermi ", Course XIV, edited by P. Caldirola, (Academic, New York, 1960); also, in A Question of Physics, edited by P. Buckley and F.D. Peat (Univ. of Toronto Press, Toronto, 1979); Acta Phys. Polonica 15, 3 (1955).
[80] I. Prigogine, From Being to Becoming (Freeman, San Francisco, 1980).
[81] S. A. Hassan, A. R. Vasconcellos, and R. Luzzi, Physica A, 262, 359 (1999).
[82] R. Jancel, Foundations of Classical and Quantum Statistical Mechanics (Pergamon, Oxford, 1963).
[83] M. Criado-Sancho and J. E. Llebot, Phys. Rev. E 47, 4104 (1993).
[84] J. G. Ramos, A. R. Vasconcellos, and R. Luzzi, Braz. J. Phys. 28, 97 (1998).
[85] R. Balian, Y. Alhassid, and H. Reinhardt, Phys. Rep. 131, 1 (1986).
[86] I. Müller and T. Ruggieri, Extended Thermodynamics (Springer, Berlin, 1993).
[87] D. Jou, J. Casas-Vázquez, and G. Lebon, Extended Irreversible Thermodynamics (Springer, Berlin, 1993; second revised and enlarged edition: Springer, Berlin, 1996).
[88] D. Jou and J. Casas-Vázquez, Phys. Rev. A 45, 8371 (1992); ibid. E 48, 3201 (1993); J. Casas-Vázquez and D. Jou, ibid. E 49, 1040 (1994).
[89] B. C. Eu, Phys. Rev. E 51, 768 (1995); Kinetic Theory and Irreversible Thermodynamics (Wiley, New York, 1992); J. Chem. Phys.102, 7169 (1995).
[90] E. T. Jaynes, "The evolution of Carnot's principle", in Maximum-Entropy and Bayesian Methods, edited by G. J. Erickson, and C. R. Smith (Kluwer, Dordrecht, 1988).
[91] T. Dedeurwaerdene, J. Casas-Vázquez, D. Jou, and G. Lebon, Phys. Rev. E 53, 498 (1996).
[92] R. Dominguez and D. Jou, Phys. Rev. E 51, 158 (1995); M. Zakari and D. Jou, J. Non-Equilib. Thermodyn. 20, 342 (1995).
[93] R. Luzzi and A. R. Vasconcellos, Physica A, 235, 345 (1997).
[94] E. Shannon, and W. Weaver, The Mathematical Theory of Communications (Univ. Illinois Press, Urbana, 1949).
[95] J. L. del Rio and L. S. Garcia-Colin, Phys. Rev. A 43, 6657 (1991); ibid. E 47, 819 (1993).
[96] A. R. Vasconcellos and R. Luzzi, Physica A 180, 182 (1992).
[97] A. J. Sampaio and R. Luzzi, J. Phys. Chem. Sol. 44, 479 (1983); A. C. S. Algarte and R. Luzzi, Phys. Rev. B 27, 7563 (1983); R. Luzzi, in High Excitation and Short Pulse Phenomena, edited by M. Pilkuhn (North Holland, Amsterdam, 1985); R. Luzzi, in Recent developments in nonequilibrium thermodynamics, edited by J. Casas-Vázquez and D. Jou (Springer, Berlin, 1986); A. R. Vasconcellos, A. C. Algarte, and R. Luzzi, Phys. Rev. B 48, 10873 (1993); A. C. Algarte, Phys. Rev. B 43, 2408 (1991); L. G. Rego and A. C. Algarte, Phys. Rev. B 49, 7257 (1994); T. Tomé, A. R. Vasconcellos, and R. Luzzi, Physica B 144, 376 (1987); A. S. Esperidião, A. R. Vasconcellos, and R. Luzzi, J. Phys. Chem. Sol. 53, 1111 (1992); L. Lauck, A. R. Vasconcellos, and R. Luzzi, Phys. Rev. B 46, 6150 (1992).
[98] A. C. Algarte, A. R. Vasconcellos, and R. Luzzi, "Irreversible thermodynamics of the photoinjected plasma in semiconductors", review article for future publication, and A. P. Silva Ph.D. thesis (Unicamp, Campinas, São Paulo, Brazil, 1998).
[99] A. R. Vasconcellos, R. Luzzi, and A. S. Esperidião, Phys. Rev. B 52, 5021 (1995).
[100] A. R. Vasconcellos, R. Luzzi, D. Jou, and J. Casas-Vázquez, Phys. Rev. B 52, 5030 (1995).
[101] A. R. Vasconcellos, A. C. Algarte, and R. Luzzi, Phys. Rev. B 52, 13936 (1957);
[102] V. N. Freire, A. R. Vasconcellos, and R. Luzzi, Phys. Rev. B 39, 13264 (1988).
[103] D. N. Zubarev's Obituary in Teor. Mat. Fiz. 96, 321 (1993) [English transl.: Theor. Math. Phys. 96, 995 (1994)].
[104] H. Barnum, C. M. Caves, C. Fuchs, and R. Schack; D. J. Driebe; W. G. Hoover, H.Posch, and B. L.Holian; R. Peierls; J. L. Lebowitz, in Letters Section of Phys. Today 47 (11), pp. 11-15 and 115-117, November 1994.
[105] J. L. Lebowitz and O. Penrose, Phys. Today, 26 (2), 23 (1973).
[106] C. Truesdell, Rational Thermodynamics (McGraw-Hill, New York, 1985).
[107] L. Tisza, in Thermodynamics: History and Philosophy, edited by K. Martinas, L. Ropolyi, and P. Szegedy (World Scientific, Singapore, 1991).
[108] J. P. Dougherty, in Maximum Entropy and Bayesian Methods, edited by J. Skilling (Kluwer, Dordrecht, 1989); also Stud. Hist. Phil. Sci. 40, 843 (1993).
[109] J. G. Ramos, A. R. Vasconcellos, and R. Luzzi, "On the foundations of some approaches to nonequilibrium statistical mechanics", future publication.
[110] P. Motisuke, C. A. Argüello, and R. Luzzi, Solid State Commun. 23, 617 (1977).
[111] S. P. Heims and E. T. Jaynes, Rev. Mod. Phys. 34, 143 (1962) : subsection b, pp. 148-150, and Appendix B, p. 164 (It should be noticed a misprint in the third line of their Eq. (B1) which must end in xn-1).
[112] A. C. Algarte, A. R. Vasconcellos, and R. Luzzi, Phys. Rev. B 54, 11311 (1996); see also Refs. [52] and [92].
- [1] J. Meixner, "Thermodynamics of irreversible processes has many faces", in Irreversible Aspects of Continuum Mechanics, edited by H. Parkus and L. I. Sedov (Springer, Wien, 1968); Rheol. Acta 12, 465 (1973);
- [2] S. G. Brush, The Kind of Motion We Call Heat (North Holland, Amsterdam, 1976).
- [3] L. D. Landau, Zh. Eksp. Teor. Fiz.7, 203 (1937);
- A. A. Dougal and L. Goldstein, Phys. Rev. 109, 615 (1958).
- [4] H. B. G. Casimir and F. K. du Pre, Physica 5, 507 (1938);
- also A. Abragam, The Principles of Nuclear Magnetism (Oxford Univ. Press, Oxford, 1961).
- [5] C. S. Wang-Chang, G. E. Uhlenbeck, and J. de Boer, in Studies of Statistical Mechanics, Vol. 2, edited by J. de Boer and G. E. Uhlenbeck (North Holland, Amsterdam, 1964).
- [6] H. Fröhlich, Proc. Roy. Soc. (London) 188A, 521 (1947).
- [7] V. A. Shklovskii, Fiz. Tver. Tela 17, 3076 (1975) [Soviet Phys. Solid State 17, 2040 (1976)].
- [8] J. Shah and R. C. C. Leite, , Phys. Rev. Lett. 22, 1304 (1969).
- [9] J. Shah, R. C. C. Leite, and J. F. Scott, Solid State Commun. 8, 1089 (1970).
- [10] J. Meixner, in Foundations of Continuum Thermodynamics, edited by J. J. Domingos, M. N. Nina, and J. H. Whitelaw, (McMilland, London, 1974).
- [11] I. Müller, Arch. Ration. Mech. Anal. 40, 1 (1971).
- [12] W. Muschik, Arch. Ration. Mech. Anal. 66, 379 (1977);
- J. Non-Equilib. Thermodyn. 4, 277 (1979).
- [13] J. Keizer, J. Chem. Phys. 65, 4431 (1976);
- ibid. 69, 2609 (1978); ibid. 82, 2751 (1985); also, Statistical Thermodynamics of Nonequilibrium Processes (Springer, New York, 1987).
- [14] J. Casas-Vázquez and D. Jou, J. Phys. A: Math. Gen. 14, 1221 (1981);
- D. Jou and J. Casas-Vázquez, Phys. Rev. A 45, 8371 (1992);
- J. Casas-Vázquez and D. Jou, Phys. Rev. E 49, 1040 (1994).
- [15] D. Jou, J. Casas-Vázquez, and G. Lebon, Rep. Prog. Phys. 51, 1105 (1988);
- Contemporary Phys. 33, 411 (1992).
- [16] J. G. Kirkwood, J. Chem. Phys. 14, 180 (1946);
- [17] M. S. Green, J. Chem. Phys. 20 , 1281 (1952);
- [18] R. Zwanzig, in Lectures in Theoretical Physics, Vol. 3, edited by W. E. Brittin, B. W. Downs, and J. Downs, (Wiley-Interscience, New York, 1961).
- [19] H. Mori, , Prog. Theor. Phys. (Japan) 33, 423 (1965).
- [20] N. N. Bogoliubov, in Studies in Statistical Mechanics I, edited by J. de Boer and G. E. Uhlenbeck (North Holland, Amsterdam, 1962),
- [21] R. Luzzi and A. R. Vasconcellos, Fortschr. Phys./ Prog. Phys. 38, 887 (1990).
- [22] E. T. Jaynes, "Predictive Statistical Physics" in Frontiers of Nonequilibrium Statistical Physics, edited by J. T. Moore and M. O. Scully, (Plenum, New York, 1986).
- [23] E. T. Jaynes, reprinted articles and notes in E.T. Jaynes' Papers on Probability, Statistics, and Statistical Physics, edited by D. Rosenkrantz (Reidel, Dordrecht, 1983).
- [24] E. T. Jaynes, and papers by other authors in, The Maximum Entropy Formalism, edited by R.D. Levine and M. Tribus (MIT Press, Cambridge, MA, 1978).
- [25] W. T. Grandy, Foundations of Statistical Mechanics, Vol. I: Equilibrium Theory and Vol. II: Nonequilibrium Phenomena (Reidel, Dordrecht 1987 and 1988 respectively); also Phys. Rep.62, 175 (1980).
- [26] A. Hobson, J. Chem. Phys. 45, 1352 (1966);
- Am. J. Phys. 34, 411 (1966).
- [27] E. T. Jaynes, Phys. Rev. 106, 620 (1957); ibid. 108, 171 (1957).
- [28] L. S. Garcia-Colin, A. R. Vasconcellos, and R. Luzzi, J. Non-Equilib. Thermodyn. 19, 23 (1994);
- R. Luzzi, A. R. Vasconcellos, and J. G. Ramos, Fortsch. Phys./Prog. Phys., 47, 401 (1999);
- R. Luzzi, A. R. Vasconcellos, and J. G. Ramos, Statistical Foundations of Irreversible Thermodynamics, Texte zur Physik Series, edited by W. Ebeling, (Teubner Verlag, Leipizig, 2000).
- [29] S. Sieniutjcz and P. Salamon, introductory lecture in Advances in Thermodynamics, Vol. 3: Nonequilibrium Theory and Extremum Principles, edited by S. Sieniutjcz and P. Salamon (Taylor and Francis, New York, 1990).
- [30] R. E. Nettleton and S. L. Sobolev, J. Non-Equilib. Thermodyn. 20, 205 (1995).
- [31] A. R. Vasconcellos, R. Luzzi, and L. S. Garcia-Colin, (1) Phys. Rev. A 43, 6622 (1991);
- (2) ibid. A 43, 6633 (1991); (3) J. Non-Equilib. Thermodyn. 20, 103 (1995);
- (4) ibid. 20, 119 (1995); (5) J. Mod. Phys. B 9, 1933 (1995);
- (6) ibid. 9, 1945 (1995); (7) Physica A 221, 478 (1995);
- [32] D. N. Zubarev and M.Yu. Novikov, Fortschr. Phys./Prog. Phys. 21, 703 (1973).
- [33] D. N. Zubarev, Neravnovesnaia Statisticheskaya Termodinamika (Izd. Nauka, Moscow, 1971) [English Transl.: Nonequilibrium Statistical Thermodynamics (Consultants Bureau, New York, 1974), Ch. IV.
- [34] D. N. Zubarev and V. P. Kalashnikov, Teor. Mat. Fiz. 1, 137 (1969) [Theor. Math. Phys. (USSR) 1, 108 (1970)].
- [35] D. N. Zubarev, in Reviews of Science and Technology: Modern Problems in Mathematics, Vol. 15 (in Russian), edited by R. B. Gamkreludze (Izd. Nauka, Moscow, 1980) [English Transl. Soviet Math. 16, 1509 (1991)].
- [36] D. N. Zubarev, V. Morosov, and G. Röpke, Statistical Mechanics of Nonequilibrium Processess, Vol. 1: Basic Concepts, Kinetic Theory and Vol. 2: Relaxation and Hydrodynamic Processes (Akademie Verlag, Berlin, 1996 and 1997 respectively).
- [37] J. G. Ramos, A. R. Vasconcellos, and R. Luzzi, Fortschr. Phys./Prog. Phys., 43, 265 (1995).
- [38] R. Luzzi, A. R. Vasconcellos, and J. G. Ramos, Foundations of a Nonequilibrium Ensemble Formalism, Fundamental Theories of Physics Series, van der Merwe, A., Ed. (Kluwer Academic, Dordrecht), book of future publication.
- [39] A. I. Akhiezer and S. V. Peletminskii, Methods of Statistical Physics (Pergamon, Oxford, 1981).
- [40] J. A. McLennan, Introduction to Nonequilibrium Statistical Mechanics (Prentice-Hall, Englewoods Cliffs, 1989).
- [41] H. Mori, I. Oppenheim, and J. Ross, in Studies in Statistical Mecanics I, edited by J. de Boer and G. E. Uhlenbeck (North Holland, Amsterdam, 1962)..
- [42] G. E. Uhlenbeck, in Studies in Statistical Mechanics I, edited by M. Kac (Am. Math. Soc., Providence, RI, 1963).
- [43] L. L. Buishvili and M. D. Sviadadze, Physica 59, 697 (1972).
- [44] A. R. Vasconcellos, A. C. Algarte, and R. Luzzi, Physica A 166, 517 (1990);
- R. Luzzi, A. R. Vasconcellos, and J. G. Ramos, Ukrainian Journal of Physics, in press.
- [45] S. V. Peletminskii and A. A. Yatsenko, Zh. Ekps. Teor. Fiz. 53, 1327 (1967) [Soviet Phys. JETP 26, 773 (1968)].
- [46] J. R. Madureira, A. R. Vasconcellos, and R. Luzzi, J. Chem. Phys. 109, 2099 (1998).
- [47] J. R. Madureira, A. R. Vasconcellos, R. Luzzi, J. Casas-Vázquez, and D. Jou, J. Chem. Phys. 108, 7568 (1998); ibid. 108, 7580 (1998).
- [48] C. Truesdell and R.A. Toupin, "The classical field theories", in Encyclopaedia of Physics, Vol. III/1, edited by S. Flügge (Springer, Berlin 1960).
- [49] J. G. Ramos, A. R. Vasconcellos, and R. Luzzi, "A truncation criterion in Informational Statistical Thermodynamics", J. Chem. Phys., 112, 2692 (2000).
- [50] D. N. Bogoliubov, Lectures in Quantum Statistics II (Gordon and Breach, New York, 1970).
- [51] L. Lauck, A. R. Vasconcellos, and R. Luzzi, Physica A 168, 789 (1990);
- J. R. Madureira, A. R. Vasconcellos, R. Luzzi, and L. Lauck, Phys. Rev. E, 57, 3637 (1998).
- [52] See for example the review article: A. C. Algarte, A. R. Vasconcellos, and R.Luzzi, Phys. Stat. Sol. (b) 173, 487 (1992).
- [53] R. Luzzi, A. R. Vasconcellos, and J. G. Ramos, "Statistical Irreversible Thermodynamics in a Nonequilibrium Ensemble Formalism", Rivista del Nuovo Cimento, submitted.
- [54] M. A. Tenan, A. R. Vasconcellos, and R. Luzzi, Fortschr. Phys./Prog. Phys., 47, 1 (1996).
- [55] J. G. Ramos, A. R. Vasconcellos, and L. S. Garcia-Colin, Braz. J. Phys., 27, 585 (1997).
- [56] V. P. Peletminskii and A. I. Sokolovskii, Theor. Mat. Phys. (USSR) 18, 85 (1974); see also [73].
- [57] J. Seke, Phys. Rev. A 21, 2156 (1980).
- [58] R. Courant and D. Hilbert, Methods of Theoretical Physics (Willey-Interscience, New York, 1953).
- [59] R. E. Nettleton, Can. J. Phys. 72, 106 (1994).
- [60] B. C. Eu and L. S. Garcia-Colin, "Irreversible Processes and Temperature", preprint (we thank the authors for kindly forwarding us a first version of their paper);
- and Phys. Rev. E 54, 2501 (1996).
- [61] A. R. Vasconcellos, R. Luzzi, D. Jou, and J. Casas-Vázquez, Physica A 212, 369 (1994);
- [62] R. Luzzi, M. F. Scarparo, J. G. Ramos, A. R. Vasconcellos, M. Barros, and A. Kiel, J. Non-Equilib. Thermodyn., 22, 197 (1997).
- [63] P. C. Martin, "Measurements and Correlation Functions", in Many-Body Physics, edited by C.de Witt and R. Balian (Gordon and Breach, New York, 1968);
- R. Luzzi, Tópicos em Termodinâmica Estatística de Processos Dissipativos: Teoria da Função Resposta (Edunicamp, Campinas, 2000).
- [64] R. Luzzi and A. R. Vasconcellos, J. Stat. Phys. 23, 539 (1980).
- [65] A. R. Vasconcellos, R. Luzzi, and A. S. Esperidião, Phys. Rev. B 52, 5021 (1995);
- A.R. Vasconcellos, R. Luzzi, D. Jou, and J. Casas-Vázquez, Phys. Rev. B 52, 5030 (1995).
- [66] For example, see R. R. Alfano, in New Techniques and Ideas in Quantum Measurement Theory, edited by D. M. Greenberg, Annals of the NYAS Vol. 480 (New York Acad. Sci., New York, 1986).
- [67] R. Luzzi and A. R. Vasconcellos, in Semiconductors Probed by Ultrafast Laser Spectroscopy, Vol. 1, edited by R. R. Alfano (Academic, New York, 1984).
- [68] A. C. Algarte, A. R. Vasconcellos, and R. Luzzi, Braz. J. Phys., 26, 543 (1996).
- [69] R. J. Seymour, M. R. Junnakar, and R. R. Alfano, Solid State Commun. 41, 657 (1982).
- [70] A. R. Vasconcellos, R. Luzzi, J. Casas-Vázquez, and D. Jou, Physica A, 234, 699 (1996).
- [71] E. E. Mendez, F. Agulló-Rueda, and J. M. Hong, Phys. Rev. Lett. 60, 2426 (1988).
- [72] T. Amand and J. Collet, J. Phys. Chem. Solids, 46, 1053 (1985).
- [73] A. C. Algarte, A. R. Vasconcellos, and R. Luzzi, Phys. Stat. Sol. (b), 173, 487 (1992).
- [74] C. G. Rodrigues, A. R. Vasconcellos, V. N. Freire, and R. Luzzi, Appl. Phys. Lett., submitted.
- [75] C. G. Rodrigues, A. R. Vasconcellos, V. N. Freire, and R. Luzzi, Phys. Rev. B, submitted.
- [76] A. C. Algarte, A. R. Vasconcellos, and R. Luzzi, Phys. Rev. B, 54, 11311 (1996).
- [77] R. Luzzi, J. G. Ramos, and A. R. Vasconcellos, Phys. Rev. E., 57, 244 (1998).
- [78] N. Bohr, Dialectica 2, 312 (1948).
- [79] L. Rosenfeld, in Proc. Int. School "Enrico Fermi ", Course XIV, edited by P. Caldirola, (Academic, New York, 1960);
- also, in A Question of Physics, edited by P. Buckley and F.D. Peat (Univ. of Toronto Press, Toronto, 1979);
- Acta Phys. Polonica 15, 3 (1955).
- [80] I. Prigogine, From Being to Becoming (Freeman, San Francisco, 1980).
- [81] S. A. Hassan, A. R. Vasconcellos, and R. Luzzi, Physica A, 262, 359 (1999).
- [82] R. Jancel, Foundations of Classical and Quantum Statistical Mechanics (Pergamon, Oxford, 1963).
- [83] M. Criado-Sancho and J. E. Llebot, Phys. Rev. E 47, 4104 (1993).
- [84] J. G. Ramos, A. R. Vasconcellos, and R. Luzzi, Braz. J. Phys. 28, 97 (1998).
- [85] R. Balian, Y. Alhassid, and H. Reinhardt, Phys. Rep. 131, 1 (1986).
- [86] I. Müller and T. Ruggieri, Extended Thermodynamics (Springer, Berlin, 1993).
- [87] D. Jou, J. Casas-Vázquez, and G. Lebon, Extended Irreversible Thermodynamics (Springer, Berlin, 1993; second revised and enlarged edition: Springer, Berlin, 1996).
- [88] D. Jou and J. Casas-Vázquez, Phys. Rev. A 45, 8371 (1992);
- [89] B. C. Eu, Phys. Rev. E 51, 768 (1995);
- Kinetic Theory and Irreversible Thermodynamics (Wiley, New York, 1992);
- J. Chem. Phys.102, 7169 (1995).
- [90] E. T. Jaynes, "The evolution of Carnot's principle", in Maximum-Entropy and Bayesian Methods, edited by G. J. Erickson, and C. R. Smith (Kluwer, Dordrecht, 1988).
- [91] T. Dedeurwaerdene, J. Casas-Vázquez, D. Jou, and G. Lebon, Phys. Rev. E 53, 498 (1996).
- [92] R. Dominguez and D. Jou, Phys. Rev. E 51, 158 (1995);
- M. Zakari and D. Jou, J. Non-Equilib. Thermodyn. 20, 342 (1995).
- [93] R. Luzzi and A. R. Vasconcellos, Physica A, 235, 345 (1997).
- [94] E. Shannon, and W. Weaver, The Mathematical Theory of Communications (Univ. Illinois Press, Urbana, 1949).
- [95] J. L. del Rio and L. S. Garcia-Colin, Phys. Rev. A 43, 6657 (1991);
- [96] A. R. Vasconcellos and R. Luzzi, Physica A 180, 182 (1992).
- [97] A. J. Sampaio and R. Luzzi, J. Phys. Chem. Sol. 44, 479 (1983);
- A. C. S. Algarte and R. Luzzi, Phys. Rev. B 27, 7563 (1983);
- R. Luzzi, in High Excitation and Short Pulse Phenomena, edited by M. Pilkuhn (North Holland, Amsterdam, 1985);
- R. Luzzi, in Recent developments in nonequilibrium thermodynamics, edited by J. Casas-Vázquez and D. Jou (Springer, Berlin, 1986);
- A. R. Vasconcellos, A. C. Algarte, and R. Luzzi, Phys. Rev. B 48, 10873 (1993);
- A. C. Algarte, Phys. Rev. B 43, 2408 (1991);
- L. G. Rego and A. C. Algarte, Phys. Rev. B 49, 7257 (1994);
- T. Tomé, A. R. Vasconcellos, and R. Luzzi, Physica B 144, 376 (1987);
- A. S. Esperidião, A. R. Vasconcellos, and R. Luzzi, J. Phys. Chem. Sol. 53, 1111 (1992);
- L. Lauck, A. R. Vasconcellos, and R. Luzzi, Phys. Rev. B 46, 6150 (1992).
- [98] A. C. Algarte, A. R. Vasconcellos, and R. Luzzi, "Irreversible thermodynamics of the photoinjected plasma in semiconductors", review article for future publication,
- and A. P. Silva Ph.D. thesis (Unicamp, Campinas, São Paulo, Brazil, 1998).
- [99] A. R. Vasconcellos, R. Luzzi, and A. S. Esperidião, Phys. Rev. B 52, 5021 (1995).
- [100] A. R. Vasconcellos, R. Luzzi, D. Jou, and J. Casas-Vázquez, Phys. Rev. B 52, 5030 (1995).
- [101] A. R. Vasconcellos, A. C. Algarte, and R. Luzzi, Phys. Rev. B 52, 13936 (1957);
- [102] V. N. Freire, A. R. Vasconcellos, and R. Luzzi, Phys. Rev. B 39, 13264 (1988).
- [103] D. N. Zubarev's Obituary in Teor. Mat. Fiz. 96, 321 (1993) [English transl.: Theor. Math. Phys. 96, 995 (1994)].
- [104] H. Barnum, C. M. Caves, C. Fuchs, and R. Schack; D. J. Driebe; W. G. Hoover, H.Posch, and B. L.Holian; R. Peierls; J. L. Lebowitz, in Letters Section of Phys. Today 47 (11), pp. 11-15 and 115-117, November 1994.
- [105] J. L. Lebowitz and O. Penrose, Phys. Today, 26 (2), 23 (1973).
- [106] C. Truesdell, Rational Thermodynamics (McGraw-Hill, New York, 1985).
- [107] L. Tisza, in Thermodynamics: History and Philosophy, edited by K. Martinas, L. Ropolyi, and P. Szegedy (World Scientific, Singapore, 1991).
- [108] J. P. Dougherty, in Maximum Entropy and Bayesian Methods, edited by J. Skilling (Kluwer, Dordrecht, 1989); also Stud. Hist. Phil. Sci. 40, 843 (1993).
- [109] J. G. Ramos, A. R. Vasconcellos, and R. Luzzi, "On the foundations of some approaches to nonequilibrium statistical mechanics", future publication.
- [110] P. Motisuke, C. A. Argüello, and R. Luzzi, Solid State Commun. 23, 617 (1977).
- [111] S. P. Heims and E. T. Jaynes, Rev. Mod. Phys. 34, 143 (1962)
- [112] A. C. Algarte, A. R. Vasconcellos, and R. Luzzi, Phys. Rev. B 54, 11311 (1996);
Appendix I. The Truncation Procedure
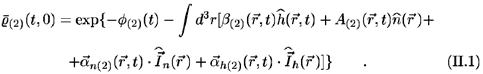
Appendix III: Extremal Constraints and Informational Entropy
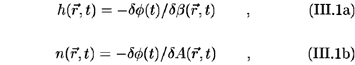
Appendix IV: Additional Considerations on the Informational Entropy (or its Entropy or Quasientropy)
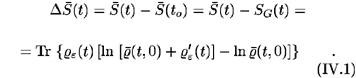
Publication Dates
-
Publication in this collection
11 Jan 2002 -
Date of issue
2000
History
-
Received
04 Apr 2000







































































































