Hostname: page-component-848d4c4894-hfldf Total loading time: 0 Render date: 2024-05-11T10:58:21.073Z Has data issue: false hasContentIssue false
  • English
  • Français

Simulating level-crossing probabilities by importance sampling

Part of: Limit theorems Probabilistic methods, simulation and stochastic differential equations

Published online by Cambridge University Press:  01 July 2016

T. Lehtonen  and
H. Nyrhinen
T. Lehtonen*
Affiliation:
Helsinki School of Economics
H. Nyrhinen*
Affiliation:
Rolf Nevanlinna Institute, Helsinki
*
∗Postal address: Helsinki School of Economics, Runebergink. 22–24, 00100 Helsinki, Finland.
∗∗Postal address: Rolf Nevanlinna Institute, Teollisuuskatu 23, 00510 Helsinki, Finland.
Get access Rights & Permissions [Opens in a new window]

Abstract

Let X1, X2, · ·· be independent and identically distributed random variables such that ΕΧ1 < 0 and P(X1 ≥ 0) ≥ 0. Fix M ≥ 0 and let T = inf {n: X1 + X2 + · ·· + Xn ≥ M} (T = +∞, if for every n = 1,2, ···). In this paper we consider the estimation of the level-crossing probabilities P(T <∞) and 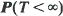, by using Monte Carlo simulation and especially importance sampling techniques. When using importance sampling, precision and efficiency of the estimation depend crucially on the choice of the simulation distribution. For this choice we introduce a new criterion which is of the type of large deviations theory; consequently, the basic large deviations theory is the main mathematical tool of this paper. We allow a wide class of possible simulation distributions and, considering the case that M →∞, we prove asymptotic optimality results for the simulation of the probabilities P(T <∞) and 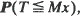. The paper ends with an example.

Keywords

MONTE CARLO SIMULATIONLARGE DEVIATIONS THEORYLEVEL-CROSSING PROBABILITY

MSC classification

Primary: 65C05: Monte Carlo methods
Secondary: 60F10: Large deviations
Type
Research Article
Information
Advances in Applied Probability , Volume 24 , Issue 4 , December 1992 , pp. 858 - 874
Copyright
Copyright © Applied Probability Trust 1992 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Asmussen, S. (1984) Approximations for the probability of ruin within finite time. Scand. Actuarial J. , 31–57.Google Scholar
[2] Asmussen, S. (1985) Conjugate processes and the simulation of ruin problems. Stoch. Proc. Appl. 20, 213–229.Google Scholar
[3] Bucklew, J. A., Ney, P. and Sadowsky, J. S. (1990) Monte Carlo simulation and large deviations theory for uniformly recurrent Markov chains. J. Appl. Prob. 27, 44–59.Google Scholar
[4] Ellis, R. S. (1985) Entropy, Large Deviations and Statistical Mechanics. Springer-Verlag, New York.CrossRefGoogle Scholar
[5] Glynn, P. W. and Iglehart, D. L. (1989) Importance sampling for stochastic simulations. Management Sci. 35, 1367–1392.CrossRefGoogle Scholar
[6] Lalley, S. P. (1984) Limit theorems for first-passage times in linear and non-linear renewal theory. Adv. Appl. Prob. 16, 766–803.Google Scholar
[7] Martin-Löf, A. (1983) Entropy estimates for ruin probabilities. In Probability and Mathematical Statistics , ed. Gut, A. and Holst, L., pp. 129–139, Dept. of Mathematics, Uppsala University.Google Scholar
[8] Martin-Löf, A. (1986) Entropy, a useful concept in risk theory. Scand. Actuarial J. , 223–235.Google Scholar
[9] Rockafellar, R. T. (1970) Convex Analysis. Princeton University Press, Princeton, NJ.CrossRefGoogle Scholar
[10] Sadowsky, J. S. (1992) On the optimality and stability of exponential twisting in Monte Carlo estimation. IEEE Trans. Inf. Theory. To appear.Google Scholar
[11] Siegmund, D. (1976) Importance sampling in the Monte Carlo study of sequential tests. Ann. Statist. 4, 673–684.Google Scholar
[12] Siegmund, D. (1975) The time until ruin in collective risk theory. Mitt. Verein. schweitz. Vers. Math. 75 (2), 157–166.Google Scholar