A Neuro-Swarming Intelligence-Based Computing for Second Order Singular Periodic Non-linear Boundary Value Problems

Sabir, Zulqurnain; Raja, Muhammad Asif Zahoor; Guirao, Juan L. G.; Shoaib, Muhammad

doi:10.3389/fphy.2020.00224

ORIGINAL RESEARCH article

Front. Phys., 07 August 2020
Sec. Statistical and Computational Physics
Volume 8 - 2020 | https://doi.org/10.3389/fphy.2020.00224

A Neuro-Swarming Intelligence-Based Computing for Second Order Singular Periodic Non-linear Boundary Value Problems

Zulqurnain Sabir¹

Muhammad Asif Zahoor Raja^2,3

Juan L. G. Guirao⁴^*

Muhammad Shoaib⁵

¹Department of Mathematics and Statistics, Hazara University, Mansehra, Pakistan
²Future Technology Research Center, National Yunlin University of Science and Technology, Douliu, Taiwan
³Department of Electrical and Computer Engineering, COMSATS University Islamabad, Attock, Pakistan
⁴Department of Applied Mathematics and Statistics, Hospital de Marina, Technical University of Cartagena, Cartagena, Spain
⁵Department of Mathematics, COMSATS University Islamabad, Attock, Pakistan

In the present investigation, a novel neuro-swarming intelligence-based numerical computing solver is developed for solving second order non-linear singular periodic (NSP) boundary value problems (BVPs), i.e., NSP-BVPs, using the modeling strength of artificial neural networks (ANN) optimized with global search efficacy of particle swarm optimization (PSO) supported with the methodology of rapid local search by interior-point scheme (IPS), i.e., ANN-PSO-IPS. In order to check the proficiency, robustness, and stability of the designed ANN-PSO-IPS, two numerical problems of the NSP-BVPs have been presented for different numbers of neurons. The outcomes of the proposed ANN-PSO-IPS are compared with the available exact solutions to establish the worth of the solver in terms of accuracy and convergence, which is further endorsed through results of statistical performance metrics based on multiple implementations.

Introduction

The singular differential equations have immense applications in a variety of areas of mathematics and physics, such as dynamics, nuclear physics, chemical reactions and atomic designs etc. The research investigations of non-linear singular periodic boundary value problems (NSP-BVPs) are mainly based on differential equation models. Due to non-linearity, singular points and the periodic nature of the mathematical models, only a few existing analytical and numerical approaches are available in literature to present the solutions of the NSP-BVPs [1–5]. A few problems are provided as Agarwal [6, 7] implemented a well-known numerical shooting approach to solve NSP-BVPs. Geng and Cui [8] presented the individuality and existence for solving the NSP-BVPs. Some other numerical techniques are employed to analyze the significance of the proposed problem NSP-BVPs [9–11]. Assadi et al. [12] exploited a fixed point iterative scheme, Xin et al. [13] a non-trivial solution of NSP-BVPs, El-Syed and Gaagar [14] provided the existence of a solution for non-linear singular differential equations, Wang et al. [15] and Wang and Ru [16] a positive solution of periodic equations. The general form of the second order non-linear NSP-BVPs is written as [8]:

\begin{array}{l} {\begin{matrix} \frac{d^{2} Ψ (x)}{d x^{2}} + \frac{p (x)}{x^{β_{1}} {(1 - x)}^{δ_{1}}} \frac{d Ψ (x)}{d x} + \frac{q (x)}{x^{β_{2}} {(1 - x)}^{δ_{2}}} Ψ (x) \\ + N (Ψ) = h (x), 0 < x < 1, \\ Ψ (0) = Ψ (1), \frac{d Ψ (0)}{d x} = \frac{d Ψ (1)}{d x}, \end{matrix} & (1) \end{array}

where p(x) and q(x) are continuous, N(Ψ) is a function of Ψ. Moreover, β₁, δ₁, β₂, and δ₂ are the positive constant values. All of the above cited analytical/numerical schemes have their precise advantages, disadvantages, merits and demerits, while a stochastic numerical solver based on the intelligent computing approach by manipulating the strength of artificial neural networks (ANNs), particle swarm optimization (PSO), and interior-point scheme, i.e., ANN-PSO-IPS, has not been implemented to solve second order NSP-BVPs.

Researchers have widely studied the meta-heuristic based computing numerical approaches along with the neural network's strength for solving the linear/non-linear mathematical models [17–24]. Some recent applications of heuristic computing are corneal models for eye surgery [25], the non-linear Riccati system [26], the Bagley-Torvik system [27], non-linear systems of Bratu type [17], prey-predator non-linear models [28], non-linear reactive transport models [29], non-linear optics models [30], non-linear singular functional differential models [31], singular non-linear systems arising in atomic physics [32], non-linear doubly singular systems [33], nanofluidic systems [34], micropolar fluid flow [35], the heartbeat model [36], the singular Lane-Emden equation based model [37], the heat conduction model of the human head [38], non-linear electric circuit models [39], finance [40], and mathematical models in Bioinformatics [41, 42]. These influences proved the value, worth and consequence of the stochastic solvers based on robustness, accuracy and convergence.

Keeping in view the value and worth of these applications, the authors worked to exploit the strength and significance of stochastic solvers for a reliable, efficient and stable approach to solve the NSP-BVPs. The present analysis for NSP-BVPs given in Equation (1) is performed via stochastic numerical solver along with utilization of the strength of artificial neural networks (ANNs) based on certain numbers of neurons, particle swarm optimization (PSO) and interior-point scheme, i.e., ANN-PSO-IPS. Some innovative influences of the presented solver are briefly summarized as:

• Novel neuro-swarm intelligent/soft computing heuristics ANN-PSO-IPS using different number of neurons are accessible for the numerical behavior of the second order NSP-BVPs.

• The overlapping outcomes of the designed ANN-PSO-IPS with the referenced exact solutions for two different variants of the second order non-linear NSP-BVPs establish the convergence, correctness and reliability.

• Authorization of accurate performance is validated through statistical observations on multiple runs of ANN-PSO-IPS in terms of Theil's Inequality Coefficient (TIC), Variance Account For (VAF), and semi-interquartile range (S-IR) and Nash Sutcliffe Efficiency (NSE) metrics.

• Besides practically accurate continuous outcomes on input training interval, ease in the concept, the smooth implementable procedure, robustness, extendibility, and stability are other worthy declarations for the proposed neuro-swarm intelligent computing heuristics.

The remaining parts of the paper are planned as: section Design Methodology defines the explanation of the proposed methodology for ANN-PSO-IPS, mathematical forms of the statistic based operators are provided in section Statistical Measures, the detailed results and discussions are given in section Results and Discussion, while the conclusions and future research plans are provided in section Conclusions.

Design Methodology

The design approach of ANN-PSO-IPS is divided into two categories for a numerical solution of the non-linear second order NSP-BVPs. In category 1, the error-based fitness function is introduced, while in the second category, the combination of an optimization scheme PSO with IPS, i.e., PSO-IPS, is provided in the sense of introductory material, applications, and pseudocode.

ANN Modeling

Mathematical models for non-linear second order NSP-BVPs are assembled with the feed-forward ANNs strength, $\hat{Ψ} (x)$ shows the continuous mapping results, and its derivatives using the log-sigmoid U(x) = (1+exp(−x))⁻¹ activation functions given as:

\begin{array}{l} \hat{Ψ} (x) = \sum_{i = 1}^{k} a_{i} U (w_{i} x + b_{i}) = \sum_{i = 1}^{k} \frac{a_{i}}{(1 + e^{- (w_{i} x + b_{i})})}, \\ \frac{d \hat{Ψ}}{d x} = \sum_{i = 1}^{k} a_{i} \frac{d}{d x} U (w_{i} x + b_{i}) = \sum_{i = 1}^{k} \frac{a_{i} w_{i} e^{- (w_{i} t + b_{i})}}{{(1 + e^{- (w_{i} t + b_{i})})}^{2}}, \\ \frac{d^{2} \hat{Ψ}}{d x^{2}} = \sum_{i = 1}^{k} a_{i} \frac{d^{2}}{d x^{2}} U (w_{i} x + b_{i}) \\ = \sum_{i = 1}^{k} a_{i} w_{i}^{2} (\frac{2 e^{- 2 (w_{i} x + b_{i})}}{{(1 + e^{- (w_{i} x + b_{i})})}^{3}} - \frac{e^{- (w_{i} x + b_{i})}}{{(1 + e^{- (w_{i} x + b_{i})})}^{2}}), & (2) \end{array}

where the weights are a = [a₁, a₂, a₃, ..., a_m], w = [w₁, w₂, w₃, ..., w_m] and b = [b₁, b₂, b₃, ..., b_m]. In order to solve the non-linear second order NSP-BVPs given in the system (1), an error-based fitness formulation using the mean square error sense is written as:

\begin{array}{l} E = E_{1} + E_{2}, & (3) \end{array}

where E₁ and E₂ are the error functions related to the differential system and the boundary conditions, respectively, written as:

\begin{array}{l} E_{1} = \frac{1}{N} \sum_{m = 1}^{N} (\frac{d^{2} {\hat{Ψ}}_{m}}{d x_{m}^{2}} + \frac{p_{m}}{x_{m}^{β_{1} {(1 - x_{m})}^{δ_{1}}}} \frac{d {\hat{Ψ}}_{m}}{d x_{m}} + \frac{q_{m}}{x_{m}^{β_{2} {(1 - x_{m})}^{δ_{2}}}} {\hat{Ψ}}_{m} \\ + N ({\hat{Ψ}}_{m}) - h_{m}), 0 < x_{m} < 1, & (4) \end{array}

\begin{array}{l} E_{2} = \frac{1}{2} {({\hat{Ψ}}_{0} - {\hat{Ψ}}_{N})}^{2} + \frac{1}{2} {(\frac{d {\hat{Ψ}}_{0}}{d x_{m}} - \frac{d {\hat{Ψ}}_{N}}{d x_{m}})}^{2}, & (5) \end{array}

where $N h = 1, p_{m} = p (x_{m}), q_{m} = q (x_{m}), h_{m} = h (x_{m}), {\hat{Ψ}}_{m} = \hat{Ψ} (x_{m}) and x_{m} = m h .$ , while $\hat{Ψ}$ is the approximate solution of Ψ of system represented in (1), N is total number of input grid points and h is the step size.

Optimization Process: PSO-IPS

The parameter optimization for second order non-linear NSP-BVPs is approved by the hybrid computing framework based on PSO and IPS.

The PSO approach [43] is applied as an effective alternative to the efficient global search mechanism of genetic algorithms [44] that is used as an optimization apparatus for the second order non-linear NSP-BVPs. Kennedy and Eberhart proposed PSO, which is a famous algorithm for the global search optimization strength, at the end of the 19th century. PSO is considered as an easy implementation process with low memory requirements [45]. This optimization algorithm exploits mathematical modeling inspired bythe swarm pattern of birds flocking as well as fish schooling. Recently, this global optimization procedure is used in different applications, like the fuel ignition model [46], non-linear physical models [47], parameter approximation systems of control auto regressive moving average models [48], balancing stochastic U-lines problems [49], operation scheduling of microgrids [50], and features classification [51].

In the search space theory, a single candidate solution is called a particle using the optimization process. For the PSO optimization approach, the prime swarms spread into the larger and for the adjustment of the parameters of PSO, the scheme delivers iteratively optimal outcomes $P_{L B}^{δ - 1}$ and $P_{G B}^{δ - 1}$ that indicate the swarm's position and velocity. The mathematical form is given as:

\begin{array}{l} X_{i}^{δ} = X_{i}^{δ - 1} + V_{i}^{δ - 1}, & (6) \end{array}

\begin{array}{l} V_{i}^{δ} = ω V_{i}^{δ - 1} + δ_{1} (P_{L B}^{δ - 1} - X_{i}^{δ - 1}) r_{1} + δ_{2} (P_{G B}^{δ - 1} - X_{i}^{δ - 1}) r_{2}, & (7) \end{array}

where the position and velocity are X_i and V_i, respectively, r₁ and r₂ are the pseudo random vectors between 0 and 1, while δ₁ and δ₂ are the acceleration constant values. The inertia weight vector is ω∈[0, 1]. The scheme performance stops when the predefined flights are obtained.

The dynamic of the optimization PSO rapidly converges by the hybridization process with the suitable local search scheme by taking PSO global best values as an initial weight. Therefore, an efficient local search approach based on interior-point scheme (IPS) is used for quick fine-tuning of the outcomes achieved by the designed optimization approach. Some recent submissions of the IPS are mixed complementarity monotone systems [52], active noise control systems [53], simulation of aircraft parts riveting [54], the economic load dispatch model [55], and non-linear system identification [56].

The pseudocode based on the combination of PSO-IPS trains the ANN as well as the crucial setting of the parameters for both PSO and IPS are provided in Table 1. The optimization method become premature using a minor change in the parameter setting, thus, it requires several experiences, replications and information on essential optimization impressions of appropriate settings for the hybrid of PSO-IPS.

TABLE 1

Table 1. Pseudo code of the optimization tool PSO-IPS to find the weights of ANNs.

Statistical Measures

The present study aims to present the statistical performance for solving both variants of second order non-linear NSP-BVPs. In this respect, three performance operators are implemented based on Theil's inequality coefficient (TIC), Nash Sutcliffe Efficiency (NSE), and Variance Account For (VAF). The mathematical notations of these operators are given as:

\begin{array}{l} TIC= \frac{\sqrt{\frac{1}{n} {\sum_{i = 1}^{n} (Ψ_{i} - {\hat{Ψ}}_{i})}^{2}}}{(\sqrt{\frac{1}{n} \sum_{i = 1}^{n} Ψ_{i}^{2}} + \sqrt{\frac{1}{n} \sum_{i = 1}^{n} {\hat{Ψ}}_{i}^{2}})} & (8) \end{array}

\begin{array}{l} {\begin{array}{l} NSE= 1 - \frac{{\sum_{i = 1}^{n} (Ψ_{i} - {\hat{Ψ}}_{i})}^{2}}{{\sum_{i = 1}^{n} ({\hat{Ψ}}_{i} - {\bar{Ψ}}_{i})}^{2}}, {\bar{Ψ}}_{i} = \frac{1}{n} \sum_{i = 1}^{n} Ψ_{i} \\ ENSE= 1 - NSE, \end{array} & (9) \end{array}

\begin{array}{l} {\begin{matrix} V A F = (1 - \frac{var (Ψ_{i} (x) - {\hat{Ψ}}_{i} (x))}{var (Ψ_{i} (x))}) * 100, \\ E V A F = | 100 - V A F | . \end{matrix} & (10) \end{array}

\begin{array}{l} {\begin{array}{l} S I R = 0.5 (Q_{3} - Q_{1}), \\ Q_{3} = 3^{r d} quartile, Q_{1} = 1^{s t} quartile . \end{array} & (11) \end{array}

Results and Discussion

In this section, the detailed results based on two variants of the second order NSP-BVPs are presented using the ANN-PSO-IPS and comparison of the proposed outcomes with the exact solutions will also be discussed.

Example 1: Consider the second order SPBVP is written as:

\begin{array}{l} {\begin{array}{l} \frac{d^{2} Ψ (x)}{d x^{2}} + \frac{2}{x^{4} {(1 - x)}^{1.5}} \frac{d Ψ (x)}{d x} \\ + \frac{1}{x^{3} {(1 - x)}^{1.5}} Ψ (x) = h (x), 0 < x < 1, \\ Ψ (0) = Ψ (1), \frac{d Ψ (0)}{d x} = \frac{d Ψ (1)}{d x} . \end{array} & (12) \end{array}

The true solution of the Equation (12) is e¹⁰^(x−^x²⁾² and the fitness function is written as:

\begin{array}{l} E = \frac{1}{N} {\sum_{i = 1}^{m} (\frac{d^{2} {\hat{Ψ}}_{m}}{d x_{m}^{2}} + \frac{2}{x_{m}^{4} {(1 - x_{m})}^{1.5}} \frac{d {\hat{Ψ}}_{m}}{d x_{m}} + \frac{1}{x_{m}^{3} {(1 - x_{m})}^{1.5}} {\hat{Ψ}}_{m} - h_{m})}^{2} \\ + \frac{1}{2} ({({\hat{Ψ}}_{0} - {\hat{Ψ}}_{N})}^{2} + {(\frac{d {\hat{Ψ}}_{0}}{d x_{m}} - \frac{d {\hat{Ψ}}_{N}}{d x_{m}})}^{2}), & (13) \end{array}

Example 2: Consider the non-linear second order SPBVP is written as:

\begin{array}{l} {\begin{matrix} \frac{d^{2} Ψ (x)}{d x^{2}} + \frac{2}{x^{2} (1 - x)} \frac{d Ψ (x)}{d x} + \frac{1}{x (1 - x)} Ψ (x) \\ + Ψ^{2} (x) = h (x), 0 < x < 1, \\ Ψ (0) = Ψ (1), \frac{d Ψ (0)}{d x} = \frac{d Ψ (1)}{d x} . \end{matrix} & (14) \end{array}

The exact solution of the above equation is e¹⁰^(x−^x²⁾² and the fitness function is written as:

\begin{array}{l} E = \frac{1}{N} \sum_{i = 1}^{m} (\frac{d^{2} {\hat{Ψ}}_{m}}{d x_{m}^{2}} + \frac{2}{x_{m}^{2} (1 - x_{m})} \frac{d {\hat{Ψ}}_{m}}{d x_{m}} \\ {+ \frac{1}{x_{m} (1 - x_{m})} {\hat{Ψ}}_{m} + {\hat{Ψ}}_{m}^{2} - h_{m})}^{2} \\ + \frac{1}{2} ({({\hat{Ψ}}_{0} - {\hat{Ψ}}_{N})}^{2} + {(\frac{d {\hat{Ψ}}_{0}}{d x_{m}} - \frac{d {\hat{Ψ}}_{N}}{d x_{m}})}^{2}) . & (15) \end{array}

In order to perform the solutions of the second order NSP-BVPs, the optimization is accomplished using the hybrid of global and local search capabilities, i.e., PSO-IPS. The process is repeated for sixty trials to generate a large dataset parameter using the ANNs. The best weight sets are provided to indicate the approximate numerical outcomes of the model (1) using 5 and 10 numbers of neurons. The mathematical formulations of the proposed numerical outcomes for 5 neurons are shown as:

\begin{array}{l} {\hat{Ψ}}_{1} (x) = \frac{5.8775}{1 + e^{- (9.3350 x - 12.870)}} + \frac{7.3743}{1 + e^{- (5.2745 x - 2.3623)}} \\ + \frac{0.1197}{1 + e^{- (- 9.8796 x + 4.4603)}} + \frac{7.1505}{1 + e^{- (- 5.5221 x + 3.2724)}} \\ - \frac{6.8433}{1 + e^{- (8.5033 x + 3.4988)}}, & (16) \end{array}

\begin{array}{l} {\hat{Ψ}}_{2} (x) = \frac{- 7.2686}{1 + e^{- (5.6952 x - 3.2662)}} + \frac{7.4887}{1 + e^{- (6.7652 x - 9.3959)}} \\ + \frac{11.9610}{1 + e^{- (- 5.7680 x + 3.3622)}} + \frac{9.0833}{1 + e^{- (4.5840 x - 2.2274)}} \\ - \frac{4.0470}{1 + e^{- (3.2902 x - 4.1080)}} . & (17) \end{array}

The mathematical formulations of the proposed numerical outcomes for 10 number of neurons are written as:

\begin{array}{l} {\hat{Ψ}}_{1} (x) = \frac{- 0.3444}{1 + e^{- (0.1021 x - 1.9508)}} + \frac{1.6234}{1 + e^{- (- 0.2443 x + 2.2795)}} + ... \\ + \frac{7.3336}{1 + e^{- (9.9170 x - 13.6069)}} & (18) \end{array}

\begin{array}{l} {\hat{Ψ}}_{2} (x) = \frac{- 3.4763}{1 + e^{- (5.7313 x - 3.7465)}} + \frac{1.0055}{1 + e^{- (- 0.0494 x - 0.1392)}} + ... \\ + \frac{0.8568}{1 + e^{- (- 0.7378 x - 2.2455)}} . & (19) \end{array}

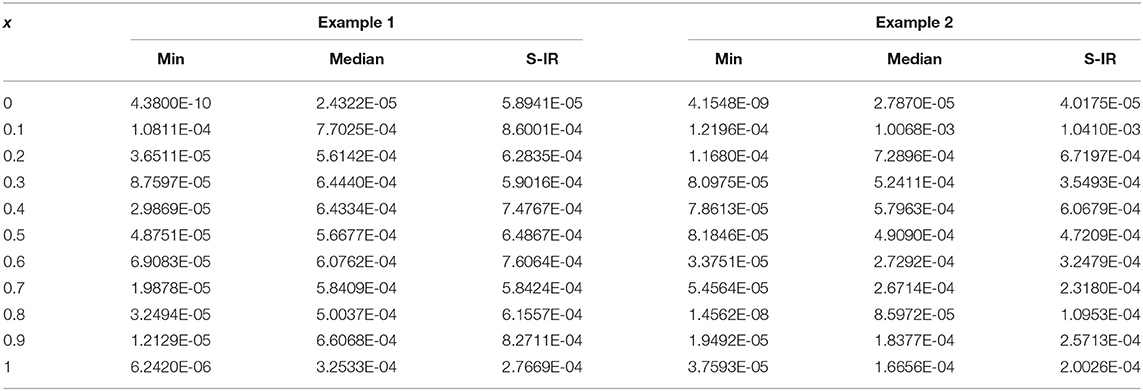
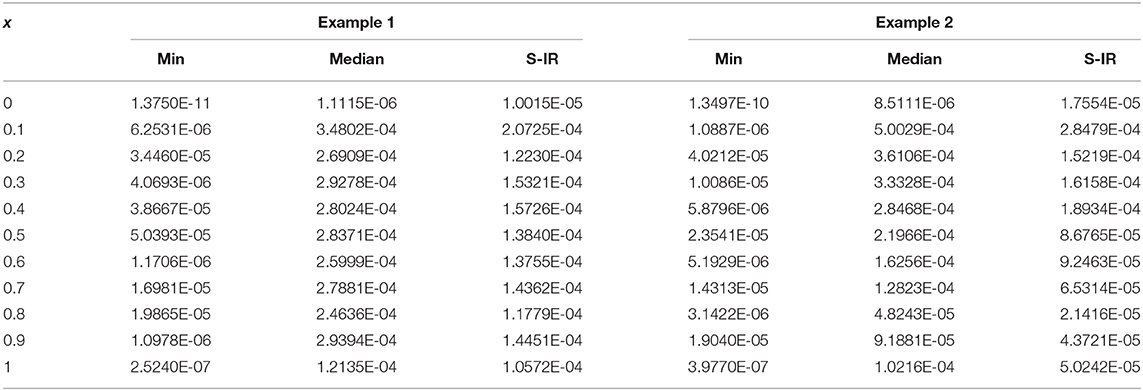
The optimization of the relations (13) and (15) is carried out with PSO-IPS for sixty trials and one set of trained weight of ANN based on 5 and 10 neurons is plotted in the Figures 1A,B, 2A,B. The comparison of the best, mean and exact solutions are drawn in the Figures 1C,D, 2C,D for 5 and 10 numbers of neurons. The best and mean results obtained by the designed approach ANN-PSO-IPS are overlapped to the exact results for both of the examples. This consistent overlapping of the results indicates the exactness and correctness of the designed scheme. The plots of absolute error (AE) for the 5 and 10 number of neurons are drawn in Figures 1E,F, 2E,F. These AE values have been obtained by using the proposed results obtained by ANN-PSO-IPS and the exact solutions. It is clear in Figures 1E,F that most of the best solutions lie around 10⁻⁰⁴−10⁻⁰⁵ for both examples, while the mean values lie around 10⁻⁰²−10⁻⁰³ and 10⁻⁰³−10⁻⁰⁴ for examples 1 and 2, respectively. The best AE values for 10 neurons are plotted in Figures 2E,F lie around 10⁻⁰⁴−10⁻⁰⁶, while the mean values lie around 10⁻⁰³−10⁻⁰⁴ for both examples. In order to find the best and mean values of the performance indices based on the VAF, ENSE, and TIC values, the Figures 1G,H, 2G,H have been plotted using the 5 and 10 number of neurons for both examples. The best ENSE, TIC, and EVAF values for 5 neurons lie around 10⁻⁰⁶−10⁻⁰⁸ for both examples. Whereas, for both examples using 5 numbers of neurons, the best ENSE values lie around 10⁻⁰²−10⁻⁰⁴ and the best TIC and EVAF values lie around 10⁻⁰⁴−10⁻⁰⁶. Furthermore, for the 10 numbers of neurons, the best values of ENSE, TIC, and EVAF are close to 10⁻⁰⁸ for example 1, while for example 2, these best values lie around 10⁻⁰⁸−10⁻⁰⁹. The mean ENSE and EVAF values for the example 1 and 2 lie around 10⁻⁰⁶−10⁻⁰⁷, while the mean TIC values lie around 10⁻⁰⁷−10⁻⁰⁸ for both examples. It is noticed that the results of AE and the performance measures for 10 neurons are found to be better when compared to 5 neurons.

FIGURE 1

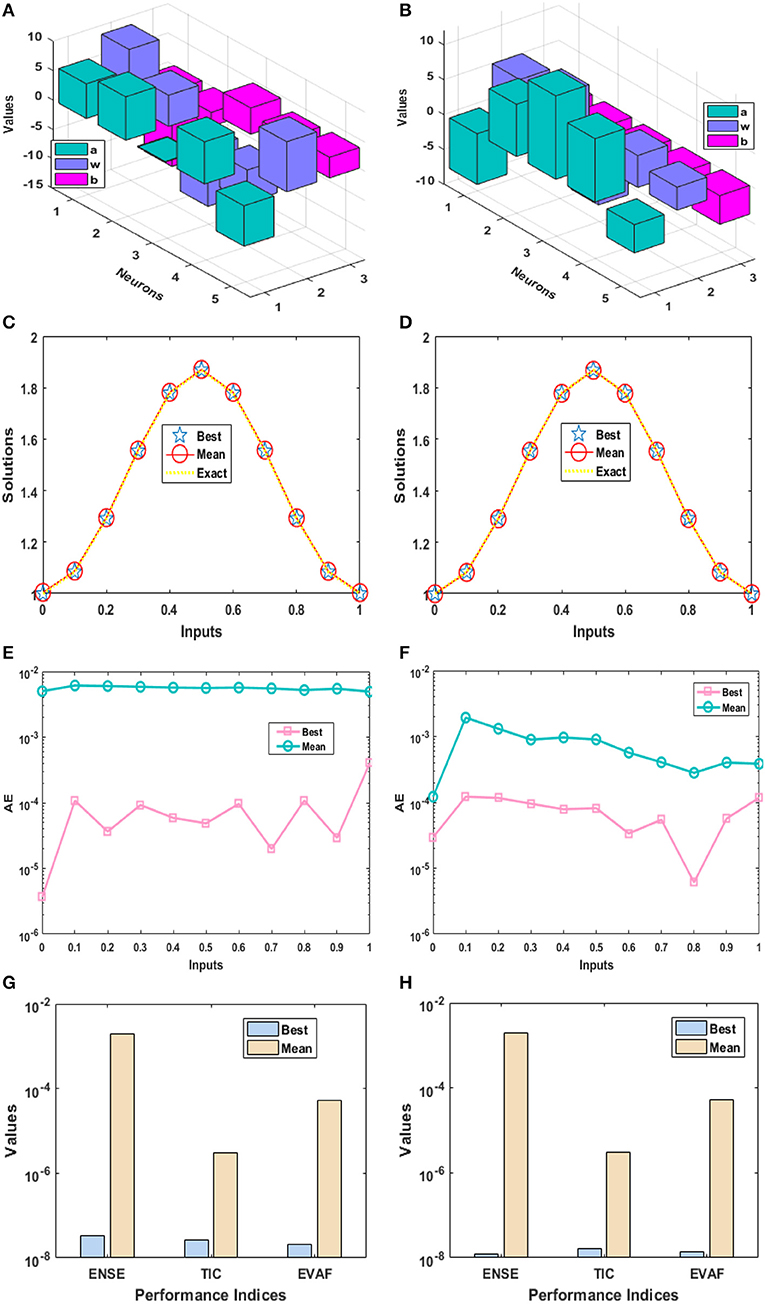
Figure 1. Best weight, results of the designed methodology, values of the AE, and performance measures of Examples 1 and 2 for 5 numbers of neurons. (A) ANN best weights for Example 1. (B) ANN best weights for Example 2. (C) Result comparison for Example 1. (D) Result comparison for Example 2. (E) AE values for Example 1. (F) AE values of for Example 2. (G) Performance measures for Example 1. (H) Performance measures for Example 2.

FIGURE 2

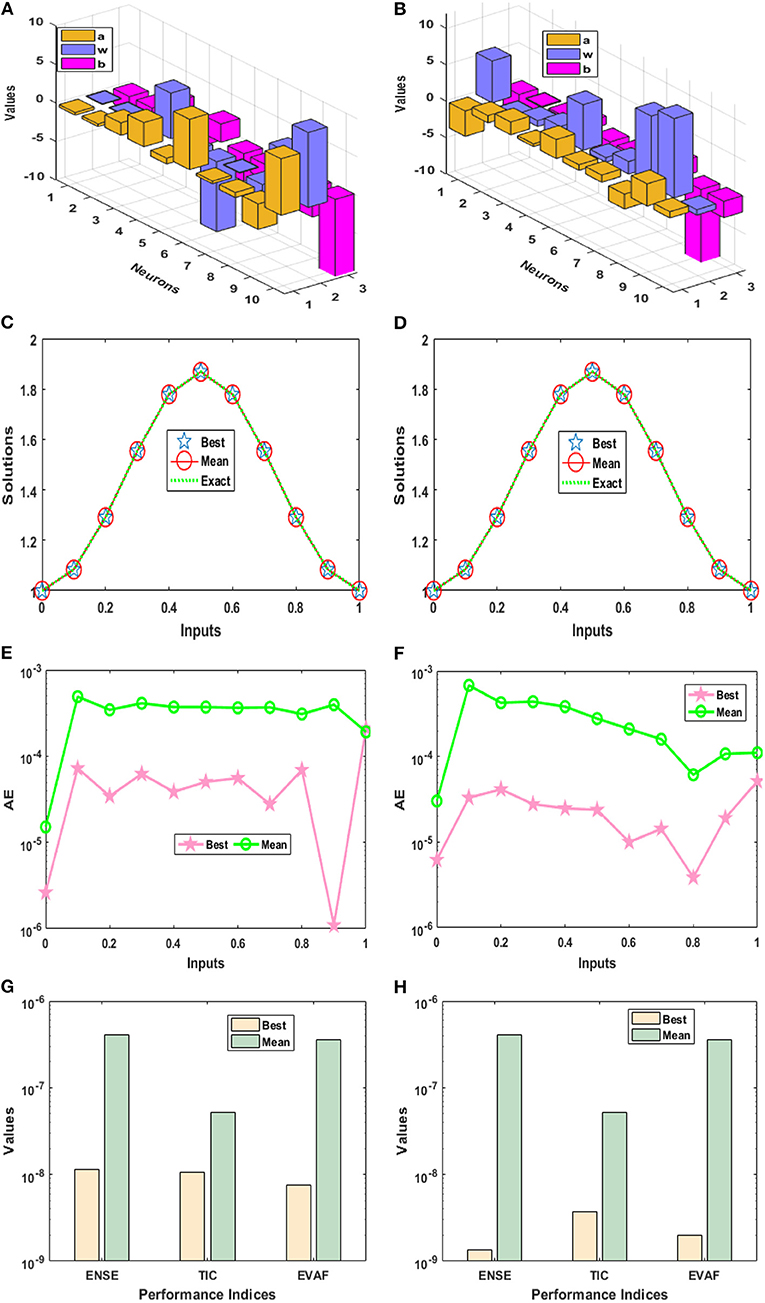
Figure 2. Best weight, results of the designed methodology, values of the AE, and performance measures of Examples 1 and 2 for 10 numbers of neurons. (A) ANN best weights for Example 1. (B) ANN best weights for Example 2. (C) Result comparison for Example 1. (D) Result comparison for Example 2. (E) AE values of 10 neurons for Example 1. (F) AE values of 10 neurons for Example 2. (G) Performance measures for Example 1. (H) Performance measures for Example 2.

Statistical investigations of the present methodology for 60 independent trials using the 5 and 10 numbers of neurons for the examples 1 and 2 are provided in Figures 3, 4. The Fitness, EVAF, ENSE, and TIC values along with the histogram are plotted in Figures 3A,B,G,H. These investigations show that around 70% of independent trials of the designed approach ANN-PSO-IPS achieved higher accuracy for all the statistical performances.

FIGURE 3

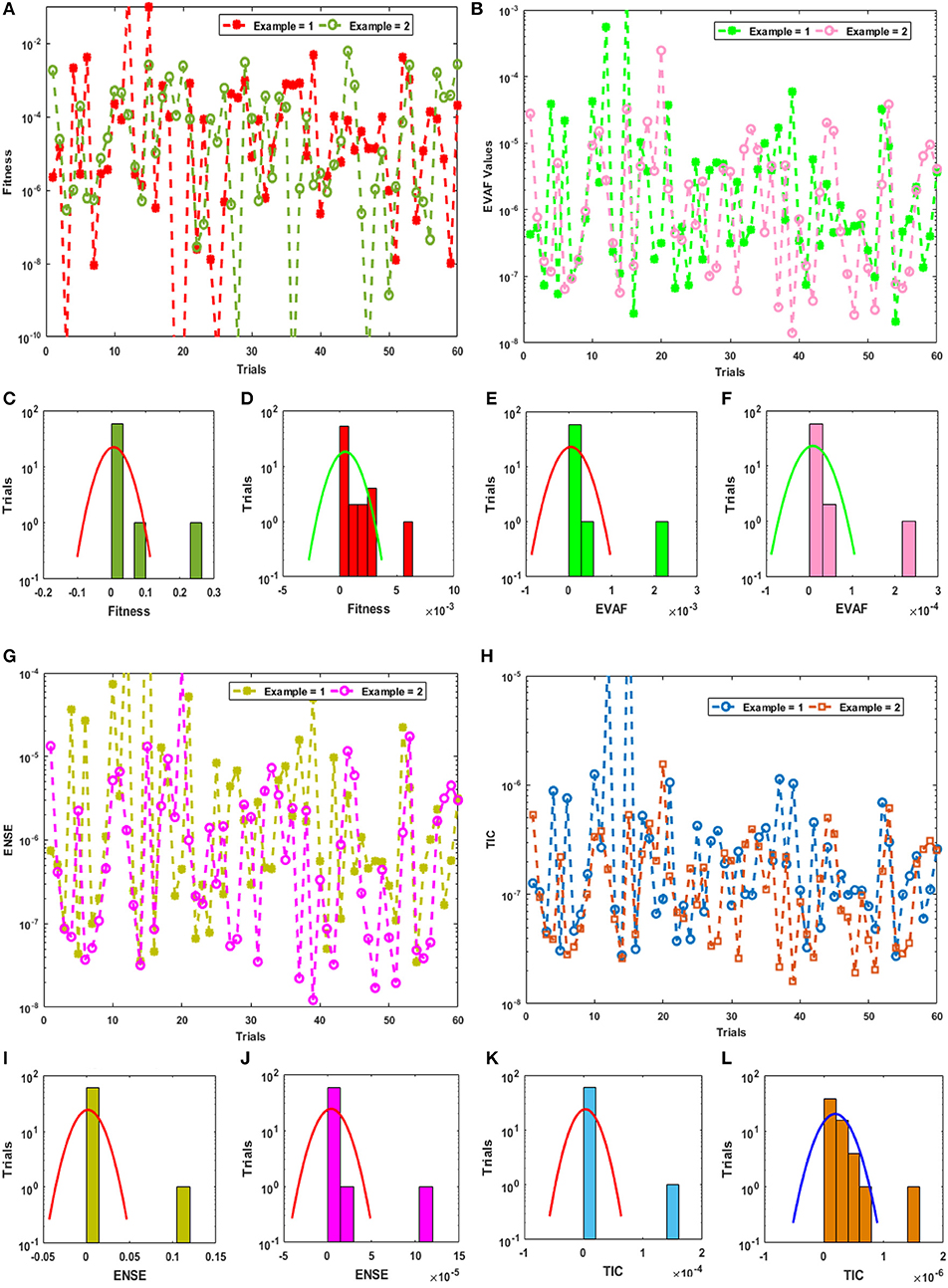
Figure 3. Statistical analysis for Fitness, EVAF, ENSE, and TIC values along with the histograms for 5 numbers of neurons. (A) Analysis through Fitness values. (B) Analysis through EVAF values. (C) Fitness histogram for Example 1. (D) Fitness histogram for Example 2. (E) EVAF histogram for Example 1. (F) EVAF histogram for Example 2. (G) Analysis through ENSE values. (H) Analysis through TIC values. (I) ENSE histogram for Example 1. (J) ENSE histogram for Example 2. (K) TIC histogram for Example 1. (L) TIC histogram for Example 2.

FIGURE 4

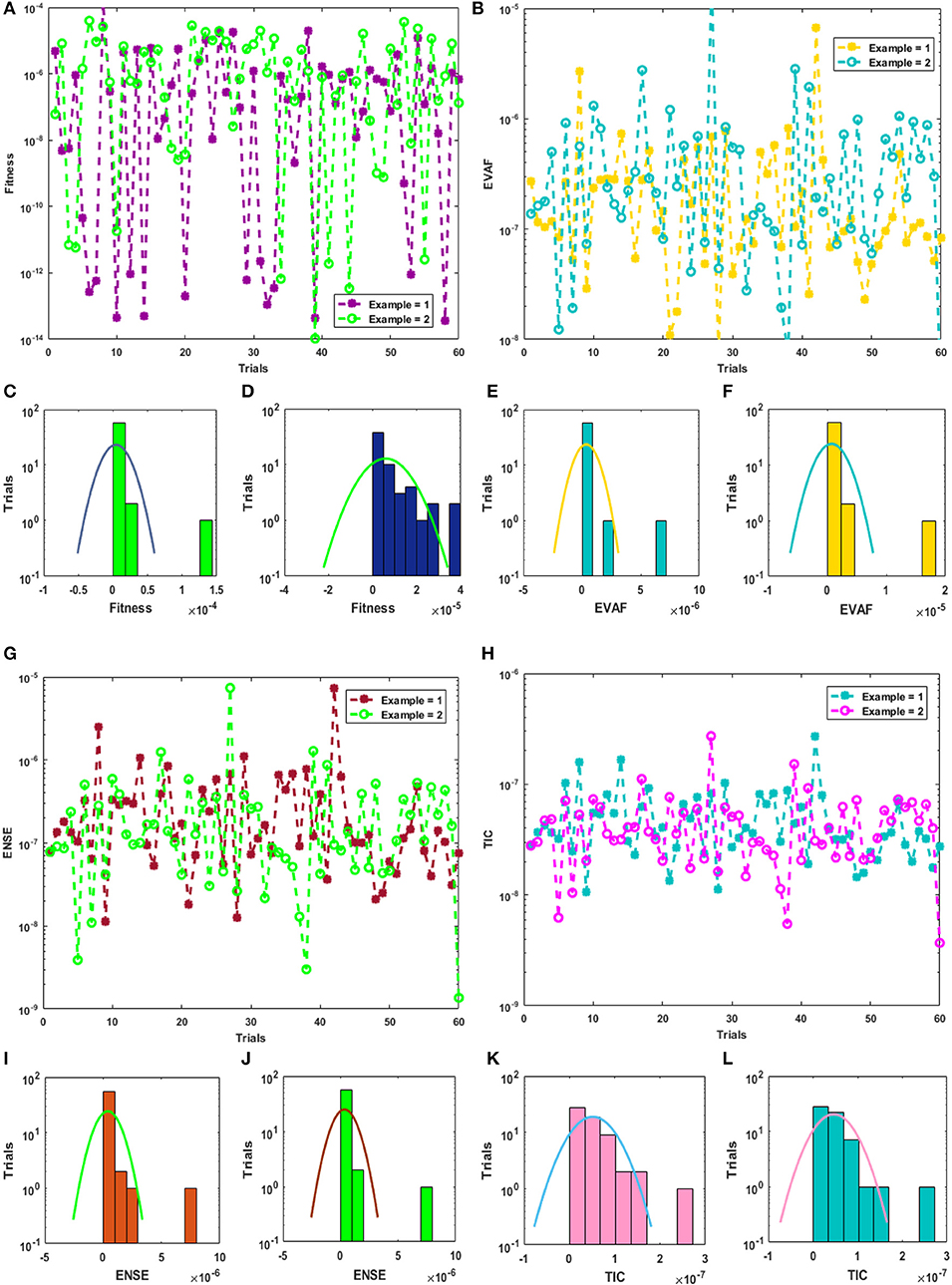
Figure 4. Statistical analysis for Fitness, EVAF, ENSE, and TIC values along with the histograms for 10 numbers of neurons. (A) Analysis through Fitness values. (B) Analysis through EVAF values. (C) Fitness histogram for Example 1. (D) Fitness histogram for Example 2. (E) EVAF histogram for Example 1. (F) EVAF histogram for Example 2. (G) Analysis through ENSE values. (H) Analysis through TIC values. (I) ENSE histogram for Example 1. (J) ENSE histogram for Example 2. (K) TIC histogram for Example 1. (L) TIC histogram for Example 2.

Statistics measures based on Minimum (Min), Median and S-IR gages for solving the second order SPBVP using the 5 and 10 numbers of neurons are tabulated in Tables 2, 3. The statistical measures are provided in order to check the accuracy analysis of the presented scheme ANN-PSO-IPS. In Table 2, the Min values for example 1 and 2 lie around 10⁻⁰⁴−10⁻¹⁰ and 10⁻⁰⁴−10⁻⁰⁹, respectively, while the Median and S-IR values lie around 10⁻⁰⁴−10⁻⁰⁵ for both examples. In Table 3, the Min values for the examples 1 and 2 lie around 10⁻⁰⁵−10⁻¹¹ and 10⁻⁰⁵−10⁻¹⁰, respectively, while the Median and S-IR values lie around 10⁻⁰⁴−10⁻⁰⁶ for both examples.

TABLE 2

Table 2. Statistical measures of second order NSP-BVPs for 5 numbers of neurons.

TABLE 3

Table 3. Statistical measures of second order SPBVP for 10 numbers of neurons.

Conclusions

A novel application of a stochastic numerical solver based on neuro-swarm intelligent computing is presented to solve the singular non-linear second order periodic boundary value problems using different numbers of neurons based on the neural networks optimized with the global search capability of particle swarm optimization supported with quick fine tuning of decision variables by manipulating the strength of local search via interior-point scheme. The singular periodic model is efficiently evaluated by the designed computing solver with the layer structure based neural networks with 5 and 10 neurons and it is found that the accuracy of numerical outcomes is enhanced by large neurons-based networks. The precision of the stochastic designed approach is verified by obtaining identical outcomes with the exact solutions having 4–6 decimal places of accuracy for solving both the singular periodic non-linear models. From the plots of performance measures using the neuron analysis, one can also conclude that the calculated accuracy is better for 10 numbers of neurons. Statistical interpretation of findings through performance indices of TIC, EVAF, and ENSE based on 60 executions/trials of the solver for obtaining the solution of singular periodic non-linear model validate the trustworthiness, accurateness and robustness. Moreover, the values of the mean, median and semi interquartile range tabulated in Tables 1, 2 provide the precise and accurate values of the presented scheme ANN-PSO-IPS.

In future, the designed approach is a promising alternate solver to be exploited/explored to investigate the computational fluid dynamics problems, especially thin film flow, wire coating analysis, squeezing flow models, Jeffery Hamel flow, calendaring problems, stretching flow problems, food processing models, and related fields [57–62].

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary materials, further inquiries can be directed to the corresponding author/s.

Author Contributions

All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.

Funding

This paper has been partially supported by Ministerio de Ciencia, Innovacion y Universidades grant number PGC2018-0971-B-100 and Fundacion Seneca de la Region de Murcia grant number 20783/PI/18.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Li F, Liang Z. Existence of positive periodic solutions to nonlinear second order differential equations. Appl Math Lett. (2005) 18:1256–64. doi: 10.1016/j.aml.2005.02.014

ORIGINAL RESEARCH article

A Neuro-Swarming Intelligence-Based Computing for Second Order Singular Periodic Non-linear Boundary Value Problems

Introduction

Design Methodology

ANN Modeling

Optimization Process: PSO-IPS

Statistical Measures

Results and Discussion

Conclusions

Data Availability Statement

Author Contributions

Funding

Conflict of Interest

References

This article is part of the Research Topic

People also looked at