Negative Effective Mass in Plasmonic Systems II: Elucidating the Optical and Acoustical Branches of Vibrations and the Possibility of Anti-Resonance Propagation
Abstract
:1. Introduction
2. Results and discussion
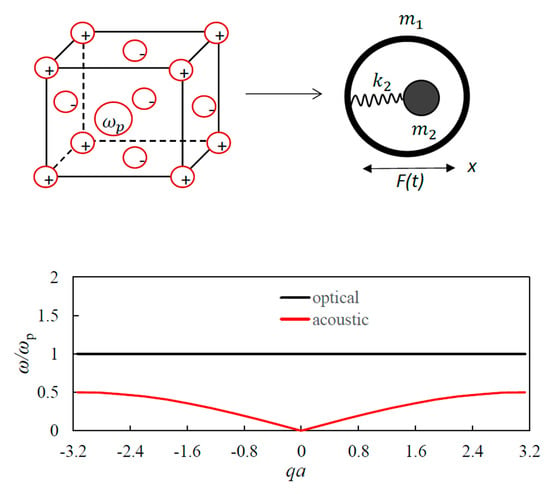
2.1. Propagation of Harmonic Waves in the 1D Lattice Comprising Negative Effective Mass Plasmonic Elements
2.2. Propagation of Harmonic Waves in the Metallic Mesostructures Demonstrating the Effect of Negative Effective Mass
3. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Felbacq, D.; Bouchitté, G. Metamaterials Modelling and Design; Taylor & Francis: Singapore; Pan Stanford Publishing: Singapore, 2017. [Google Scholar]
- Engheta, N.; Ziolkowski, R.W. Electromagnetic Metamaterials: Physics and Engineering Explorations; IEEE Press: Hoes Lane, NJ, USA, 2006. [Google Scholar]
- Kshetrimayum, R.S. A Brief Intro to Metamaterials. IEEE Potentials 2004, 23, 44–46. [Google Scholar] [CrossRef]
- Boardman, A.D.; Grimalsky, V.V.; Kivshar, Y.S.; Koshevaya, S.V.; Lapine, M.; Litchinitser, N.M.; Malnev, V.N.; Noginov, M.; Rapoport, Y.G.; Shalaev, V.M. Active and tunable metamaterials. Laser Photonics Rev. 2011, 5, 287–307. [Google Scholar] [CrossRef]
- Joannopoulos, J.D.; Villeneuve, P.R.; Fan, S. Photonic crystals. Solid State Commun. 1997, 102, 165–173. [Google Scholar] [CrossRef]
- Joannopoulos, J.; Villeneuve, P.; Fan, S. Photonic crystals: Putting a new twist on light. Nature 1997, 386, 143–149. [Google Scholar] [CrossRef]
- Baba, T. Slow light in photonic crystals. Nat. Photonics 2008, 2, 465–473. [Google Scholar] [CrossRef]
- Kushwaha, M.S.; Halevi, P.; Dobrzynski, L.; Djafari-Rouhani, B. Acoustic band structure of periodic elastic composites. Phys. Rev. Lett. 1993, 71, 2022–2025. [Google Scholar] [CrossRef] [PubMed]
- Maldovan, M. Phonon wave interference and thermal bandgap materials. Nat. Mater. 2015, 14, 667–674. [Google Scholar] [CrossRef] [PubMed]
- Sheng, P.; Zhang, X.X.; Liu, Z.; Chan, C.T. Locally resonant sonic materials. Phys. B 2003, 338, 201–205. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, X.; Mao, Y.; Zhu, Y.Y.; Yang, Z.; Chan, C.T.; Sheng, P. Locally resonant sonic materials. Science 2000, 289, 1734–1736. [Google Scholar] [CrossRef]
- Li, J.; Chan, C.T. Double-negative acoustic metamaterial. Phys. Rev. E 2004, 70, 055602. [Google Scholar] [CrossRef] [Green Version]
- Sabouni-Zawadzka, A.; Gilewski, W. Smart metamaterial based on the simplex tensegrity pattern. Materials 2018, 11, 673. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, H.; Ding, C. Simulated and experimental research of multi-band acoustic metamaterial with a single resonant structure. Materials 2019, 12, 3469. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Grima-Cornish, J.N.; Grima, J.N.; Attard, D. A Novel mechanical metamaterial exhibiting auxetic behavior and negative compressibility. Materials 2020, 13, 79. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mei, J.; Ma, G.; Yang, M.; Yang, Z.; Wen, W.; Shen, P. Dark acoustic metamaterials as super absorbers for low-frequency sound. Nat. Commun. 2012, 3, 756. [Google Scholar] [CrossRef] [Green Version]
- Zhang, S.; Yin, L.; Fang, N. Focusing ultrasound with an acoustic metamaterial network. Phys. Rev. Lett. 2009, 102, 194301. [Google Scholar] [CrossRef] [Green Version]
- Bormashenko, E.; Legchenkova, I. Negative effective mass in plasmonic systems. Materials 2020, 13, 1890. [Google Scholar] [CrossRef] [Green Version]
- Yang, Z.; Mei, J.; Yang, M.; Chan, N.H.; Sheng, P. Membrane-type acoustic metamaterial with negative dynamic mass. Phys. Rev. Lett. 2008, 101, 204301. [Google Scholar] [CrossRef]
- Chan, C.T.; Li, J.; Fung, K.H. On extending the concept of double negativity to acoustic waves. JZUS A 2006, 7, 24–28. [Google Scholar] [CrossRef]
- Huang, H.H.; Sun, C.T.; Huang, G.L. On the negative effective mass density in acoustic metamaterials. Int. J. Eng. Sci. 2009, 47, 610–617. [Google Scholar] [CrossRef]
- Tonks, L.; Langmuir, I. Oscillations in ionized gases. Phys. Rev. 1929, 33, 195–210. [Google Scholar] [CrossRef]
- Huang, Y.Y.; Sun, C.T. Wave attenuation mechanism in an acoustic metamaterial with negative effective mass density. New J. Phys. 2009, 11, 013003. [Google Scholar] [CrossRef]
- Mizutani, U. Introduction to the Electron Theory of Metals; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Ashcroft, N.; Mermin, N.D. Solid State Physics; Holt, Rinehart & Winston: New York, NY, USA, 1976. [Google Scholar]
- Kittel, C. Introduction to Solid State Physics, 5th ed.; Wiley: Hoboken, NJ, USA, 1976. [Google Scholar]
- Harrison, W.A. Solid State Theory; Dover Publications Inc.: New York, NY, USA, 1980. [Google Scholar]
- Wahl, F.; Schmidt, G.; Forrai, L. On the significance of antiresonance frequencies in experimental structural analysis. J. Sound Vib. 1999, 219, 379–394. [Google Scholar] [CrossRef]
- Belbasi, S.; Foulaadvand, M.E.; Joe, Y.S. Anti-resonance in a one-dimensional chain of driven coupled oscillators. Am. J. Phys. 2014, 82, 32–38. [Google Scholar] [CrossRef]
- Haynes, W.M. CRC Handbook of Chemistry and Physics, 92nd ed.; CRC: Boca Raton, FL, USA, 2011. [Google Scholar]
- Pendry, B.; Holden, A.J.; Stewart, W.J.; Youngs, I. Extremely low frequency plasmons in metallic mesostructures. Phys. Rev. Lett. 1996, 76, 4773. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, Z.; Zhang, X.; Mao, Y.; Zhu, Y.Y.; Yang, Z.; Chan, C.T.; Sheng, P.; Ambrosy, A.; Holdik, K. Piezoelectric PVDF films as ultrasonic transducers. J. Phys. E 1984, 17, 856–859. [Google Scholar]
- Odagawa, H.; Yamanouchi, K. 10 GHz range extremely low-loss surface acoustic wave filter. Electron. Lett. 1998, 34, 865–866. [Google Scholar] [CrossRef]
- Veselago, V.; Braginsky, L.; Shklover, V.; Hafner, C. Negative refractive index materials. J. Comput. Theor. Nanosci. 2006, 3, 189–218. [Google Scholar] [CrossRef]
- Landau, L. On the vibration of the electronic plasma. JETP 1946, 16, 574, English translation in J. Phys. (USSR) 1946, 10, 25. [Google Scholar]
- Ferrell, R.A. Predicted radiation of plasma oscillations in metal films. Phys. Rev. 1958, 111, 1214. [Google Scholar] [CrossRef]
- Politano, A.; Chiarello, G. Plamonic modes in graphene: Status and prospect. Nanoscale 2014, 6, 10927–10940. [Google Scholar] [CrossRef]
- Zhu, X.; Yan, W.; Mortensen, N.A.; Xiao, S. Bends and splitters in graphene nanoribbon waveguides. Opt. Express 2013, 21, 3486–3491. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xiao, S.; Zhu, X.; Li, H.; Mortensen, N.A. Graphene-plasmon polaritons: From fundamental properties to potential applications. Front. Phys. 2016, 11, 117801. [Google Scholar] [CrossRef] [Green Version]
- Kukhar, I.; Kryuchkov, S.V. Plasmons in a graphene bilayer in a transverse electric field. Phys. Solid State 2020, 62, 196–199. [Google Scholar] [CrossRef]





| Metal | ρ, kg/m3 | m−3 | p, Hz |
|---|---|---|---|
| Li | 530 | 4.7 × 1028 | 1.0 × 1016 |
| Au | 19,300 | 5.9 × 1028 | 1.3 × 1016 |
| Metal | D, m | a, m | m1, kg | m2, kg | k1, N/m (PDMS) | k1, N/m (Glass) | k2, N/m (Plasma) | ω1, Hz (PDMS) | ω1, Hz (Glass) |
|---|---|---|---|---|---|---|---|---|---|
| Au | 1 × 10−6 | 1.5 × 10−6 | 1.01 × 10−14 | 2.81 × 10−20 | 1.18 | 1.1 × 105 | 3.65 × 10−4 | 1.72 × 106 | 5.25 × 108 |
| Li | 1 × 10−6 | 1.5 × 10−6 | 2.77 × 10−16 | 2.24 × 10−20 | 1.18 | 1.1 × 105 | 2.24 × 10−4 | 1.04 × 107 | 3.17 × 109 |
| Au | 5 × 10−7 | 7.5 × 10−7 | 1.26 × 10−15 | 3.51 × 10−21 | 0.59 | 5.5 × 104 | 4.57 × 10−5 | 3.44 × 106 | 1.05 × 109 |
| Li | 5 × 10-7 | 7.5 × 10−7 | 3.46 × 10−17 | 2.80 × 10−21 | 0.59 | 5.5 × 104 | 2.80 × 10−5 | 2.08 × 107 | 6.34 × 109 |
| Au | 1 × 10−7 | 1.5 × 10−7 | 1.01 × 10−17 | 2.81 × 10−23 | 0.12 | 1.1 × 104 | 3.65 × 10−7 | 1.72 × 107 | 5.25 × 109 |
| Li | 1 × 10−7 | 1.5 × 10−7 | 2.77 × 10−19 | 2.24 × 10−23 | 0.12 | 1.1 × 104 | 2.24 × 10−7 | 1.04 × 108 | 3.2 × 1010 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bormashenko, E.; Legchenkova, I.; Frenkel, M. Negative Effective Mass in Plasmonic Systems II: Elucidating the Optical and Acoustical Branches of Vibrations and the Possibility of Anti-Resonance Propagation. Materials 2020, 13, 3512. https://doi.org/10.3390/ma13163512
Bormashenko E, Legchenkova I, Frenkel M. Negative Effective Mass in Plasmonic Systems II: Elucidating the Optical and Acoustical Branches of Vibrations and the Possibility of Anti-Resonance Propagation. Materials. 2020; 13(16):3512. https://doi.org/10.3390/ma13163512
Chicago/Turabian StyleBormashenko, Edward, Irina Legchenkova, and Mark Frenkel. 2020. "Negative Effective Mass in Plasmonic Systems II: Elucidating the Optical and Acoustical Branches of Vibrations and the Possibility of Anti-Resonance Propagation" Materials 13, no. 16: 3512. https://doi.org/10.3390/ma13163512