Author Contributions
Conceptualization, T.R.; Formal analysis, W.P.; Investigation, W.P.; Methodology, W.P. and T.R.; Validation, J.P. and T.R.; Visualization, J.P.; Writing—original draft, W.P.; Review & editing by all authors; All authors have read and agreed to the published version of the manuscript.
Figure 1.
Time history of (left) and 2 delay functions (right) used in Example 1.
Figure 1.
Time history of (left) and 2 delay functions (right) used in Example 1.
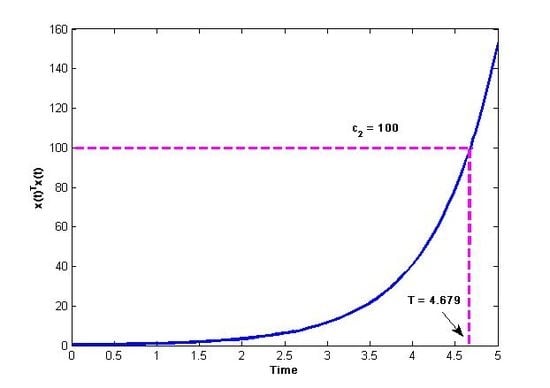
Figure 2.
Time history of (left) and state variables (right) with for (Example 2).
Figure 2.
Time history of (left) and state variables (right) with for (Example 2).
Figure 3.
Time history of (left) and state variables (right) with IC of Example 3.
Figure 3.
Time history of (left) and state variables (right) with IC of Example 3.
Table 1.
Smallest values of guarantee RFTS with respect to (Example 1: case 1).
Table 1.
Smallest values of guarantee RFTS with respect to (Example 1: case 1).
| Theorem 1 () | Corollary 1 () | Therorem 7 [9] | Theorem 1 [10] |
|---|
| 10 | | | | |
| 20 | | | | 44469 |
Table 2.
Smallest values of guarantee RFTS and RFTU with respect to , . (Example 1: case 2). NF means ’not FTS’.
Table 2.
Smallest values of guarantee RFTS and RFTU with respect to , . (Example 1: case 2). NF means ’not FTS’.
| | | 2 | 4 | 6 | 8 | 10 |
|---|
| RFTS | Theorem 1 | | | | | |
| Corollary 1 | | | | | |
| Theorem 3 [9] | NF | NF | NF | NF | NF |
| RFTU | Theorem 1 | | | | | |
| Corollary 1 | | | | | |
Table 3.
Values of smallest
guaranteeing FTS of the linear system (
1) with respect to
for
(Example 2).
Table 3.
Values of smallest
guaranteeing FTS of the linear system (
1) with respect to
for
(Example 2).
| 1 | 2 | 3 | 4 | 5 |
|---|
| Stojanovic [9] | | | | | |
| Puangmalai et al. [17] | | | | | |
| Zhang et al. [10] | | | | | |
| Corollary 1 | | | 154 | 753 | 3727 |
| | | | | |
Table 4.
Smallest upper bounds of computed for given guaranteeing RFTS with respect to of linear system with uncertainties (example 3: case 1). NF means ’not FTS’.
Table 4.
Smallest upper bounds of computed for given guaranteeing RFTS with respect to of linear system with uncertainties (example 3: case 1). NF means ’not FTS’.
| | | Computed and Value of () |
|---|
| Fixed | Theorem 1 | Corollary 1 | Fixed | Theorem 1 | Corollary 1 |
| 1 | | | | 7 | NF | |
| 2 | 75 | | | 54 | NF | |
| 3 | 400 | | | 320 | NF | |
| 4 | 2000 | | | 1750 | NF | |
| 5 | 9500 | | | 9330 | | NF |
Table 5.
Maximum
guarantees RFTS of the delay linear system (
1) with respect to
for fixed
(Example 3: case 1).
Table 5.
Maximum
guarantees RFTS of the delay linear system (
1) with respect to
for fixed
(Example 3: case 1).
| 10 | 50 | 100 | 500 | 1000 | 5000 | 10,000 | 50,000 |
|---|
| Theorem 1 | | | | | | | | |
| | | | | | | | |
| Corollary 1 | | | | | | | | |
| | | | | | | | |
Table 6.
Smallest upper bounds of computed for given guaranteeing FTS with respect to of linear system with uncertainties and controller (Example 3: case 2). NF means ’not FTS’.
Table 6.
Smallest upper bounds of computed for given guaranteeing FTS with respect to of linear system with uncertainties and controller (Example 3: case 2). NF means ’not FTS’.
| | | Computed and Value of () |
|---|
| Fixed | Theorem 1 | Corollary 1 | Fixed | Theorem 1 | Corollary 1 |
| 1 | | | | | NF | |
| 2 | 16 | | | | NF | |
| 3 | 64 | | | | NF | |
| 4 | 245 | | | | NF | |
| 5 | 900 | | | | NF | |
Table 7.
Smallest values of guaranteeing FTS of linear system with respect to (Example 3: case 3) for fixed .
Table 7.
Smallest values of guaranteeing FTS of linear system with respect to (Example 3: case 3) for fixed .
| 1 | 2 | 3 | 4 | 5 |
|---|
| Theorem 1 | | | 391 | 1935 | 9313 |
| | | | | |
| Corollary 1 | | | 317 | 1735 | 9490 |
| | | | | |
Table 8.
Smallest upper bounds of computed for given guaranteeing FTU with respect to of linear system with controller but no uncertainty (Example 3: case 4).
Table 8.
Smallest upper bounds of computed for given guaranteeing FTU with respect to of linear system with controller but no uncertainty (Example 3: case 4).
| | | Computed and Value of () |
|---|
| Fixed | Theorem 1 | Corollary 1 | Fixed | Theorem 1 | Corollary 1 |
| 1 | | | | | NF | |
| 2 | | | | | NF | |
| 3 | | | | | NF | |
| 4 | 207 | | | | NF | |
| 5 | 759 | | | | NF | |