Combining error-driven models of associative learning with evidence accumulation models of decision-making

Abstract

As people learn a new skill, performance changes along two fundamental dimensions: Responses become progressively faster and more accurate. In cognitive psychology, these facets of improvement have typically been addressed by separate classes of theories. Reductions in response time (RT) have usually been addressed by theories of skill acquisition, whereas increases in accuracy have been explained by associative learning theories. To date, relatively little work has examined how changes in RT relate to changes in response accuracy, and whether these changes can be accounted for quantitatively within a single theoretical framework. The current work examines joint changes in accuracy and RT in a probabilistic category learning task. We report a model-based analysis of changes in the shapes of RT distributions for different category responses at the level of individual stimuli over the course of learning. We show that changes in performance are determined solely by changes in the quality of information entering the decision process. We then develop a new model that combines an associative learning front end with a sequential sampling model of the decision process, showing that the model provides a good account of all aspects of the learning data. We conclude by discussing potential extensions of the model and future directions for theoretical development that are opened up by our findings.

The effect of learning on performance is twofold. As people become more proficient with a task, their responses become faster and more accurate. Traditionally, changes in these two facets of performance have been addressed by different classes of theories. On the one hand, theories of practice and automaticity have focused on reductions in response time (RT) that occur over the course of learning (e.g., Logan, 1988, 2002). On the other hand, associative learning theories have addressed changes in choice behavior with experience (e.g., Rescorla & Wagner, 1972). Perhaps surprisingly, there is relatively little theoretical work bridging these classes of theories and attempting to explain changes in choice behavior and RT simultaneously. It is therefore an open question whether the changes in RT that arise during learning can be accounted for by associative learning processes that have explained changes in choice behavior. In this article, we investigate whether an error-driven associative learning mechanism can characterize changes in choice-RT data from a simple probabilistic category learning task. We apply Ratcliff’s (1978; Ratcliff & McKoon, 2008) diffusion model to choice-RT data spanning the entire course of learning—covering rapid early changes in performance through to stable asymptotic performance once cue–outcome contingencies have been learned. We show that learning-related changes in choice behavior and the shapes of RT distribution data can be described solely in terms of changes in the quality of information driving the decision process. Conceptually, we identify changes in the quality of information with learned changes in relative associative strength linking representations of cues to different category outcomes. In this article, we develop a new formal model that combines elements of associative learning models of categorization with evidence accumulation models of decision-making. We show that this new integrated model—a synthesis of Kruschke’s (1992) ALCOVE model of category learning and Ratcliff’s (1978) diffusion decision model—provides a close account of the data from our task, and that the quality of the fit is on par with that of a flexible implementation of the diffusion model.

Two approaches to studying learning

Our theoretical starting point is the instance theory of automaticity developed by Logan (1988). The instance theory provides a detailed account of the speed-ups in performance that occur during learning (i.e., the ubiquitous practice effect; Heathcote, Brown, & Mewhort, 2000; Newell & Rosenbloom, 1981). According to instance theory, reductions in RT during learning are due to a shift from responding being controlled by a relatively slow algorithmic process to a more efficient process that is based on the retrieval of instances—and response-relevant information associated with those instances—from memory. Because instances are assumed to race independently to be retrieved, the speed of retrieval-based responding increases as more instances are accumulated in memory through repeated encounters with task-relevant stimuli (Townsend & Ashby, 1983). Logan (1988) showed that his original theory provided a good account of practice effects on mean RT in a variety of task settings. Subsequently, it was shown that the instance theory could also account for changes in the shapes of more detailed RT distribution data as a function of practice (Logan, 1992).

An important property of Logan’s (1988, 2002) instance theory is its close theoretical relationship with exemplar-based theories of categorization (e.g., Medin & Schaffer, 1978; Nosofsky, 1986). According to exemplar theories, people assign stimuli to categories on the basis of their similarity to previously encountered exemplars. Nosofsky and Palmeri (1997a, 2015) combined exemplar-based stimulus representation with the memory retrieval assumptions of Logan’s instance theory to develop the exemplar-based random walk (EBRW) model of speeded classification. In the EBRW model, presentation of a stimulus triggers a race among exemplars in memory to be retrieved. Exemplars race at a rate that is determined by their similarity to the presented item, with similar exemplars being retrieved at a faster rate than dissimilar exemplars. Once retrieved, the category label associated with the retrieved exemplar is used to drive a random walk decision process, which accumulates relative evidence about category membership to a response boundary. When a sufficient quantity of evidence has been accumulated, the corresponding category response is made. The EBRW model extended instance theory by providing a detailed account of how interitem similarity affects classification RTs as well as choice probabilities. Like instance theory, the EBRW model explains speed-ups in RT in terms of the accumulation of exemplars in memory. As learning progresses, people have access to a larger pool of exemplars to retrieve, which naturally produces faster RTs as learning progresses. Palmeri (1997, 1999) showed that the EBRW model provided an excellent account of changes in mean RTs that occurred during the development of automaticity in perceptual classification.

A key ingredient to the success of the EBRW model and instance theory is their ability to explain changes in performance via learning. Both the EBRW model and instance theory view learning as the accumulation of exemplars in memory. The assumption that exemplars race to be retrieved naturally accounts for practice effects in RT. To account for changes in categorization decisions during learning, pure exemplar-storage accounts typically need to include additional assumptions, such as the presence of “background” elements in memory that add noise to the decision process (e.g., Nosofsky, Kruschke, & McKinley, 1992). Nosofsky and Alfonso-Reese (1999) showed that by allowing retrieval of background noise elements—which become less influential over the course of learning as more exemplars are accumulated—the EBRW model was able to account for variation in both accuracy and mean RT changes during perceptual category learning. Investigation of this pure exemplar-storage view of learning is, however, somewhat limited, as relatively few studies have examined learning-related changes in accuracy in this way.

An alternative to the pure exemplar-storage view of learning is that of incremental adjustment of associations between cues and outcomes.¹ Formal models of the associative learning process have a long history in cognitive psychology (e.g., Bush & Mosteller, 1951; Estes, 1950), with the error-driven model of Rescorla and Wagner (1972) being the most prominent example. Le Pelley (2004) provided a historical overview of some of the major theoretical frameworks, noting their relative strengths and limitations. In the domain of categorization, associative learning theories are perhaps most readily identified with Kruschke’s (1992) influential ALCOVE model, which combines the exemplar-based representational assumptions of Nosofsky’s (1986) generalized context model (GCM) with an error-driven mechanism for learning both associations between exemplars and category outcomes as well as attention weights that affect computation of interitem similarity. According to association-based models of category learning, corrective feedback encountered during learning drives changes in the network of associations relating exemplars in memory to different category outcomes with the goal of minimizing prediction error. Because association weights are adjusted incrementally on a trial-by-trial basis, these models provide a natural explanation for why choice probabilities change over the course of learning. Indeed, an important benchmark for evaluating category learning models has been their ability to account for the relative rates at which category structures of differing complexity can be learned (Kruschke, 1992; Love, Medin, & Gureckis, 2004; Nosofsky, Gluck, Palmeri, McKinley, & Gauthier, 1994). Although error-driven learning is unlikely to be the only mechanism that drives changes in categorization performance (Bott, Hoffman, & Murphy, 2007; Kurtz, Levering, Stanton, Romero, & Morris, 2013), the principle has proved remarkably successful, forming the backbone of many formal models (Kruschke, 2008). Given that exemplar-retrieval theories and associative learning theories based on the ALCOVE framework share common representational assumptions (see Logan, 2002, for formal details of the relationships among specific models), it is perhaps surprising that learning models have not been rigorously tested against RT data. There are, however, practical challenges that have limited use of RT data to evaluate learning models. Chief among them, as discussed by Maddox, Ashby, and Gottlob (1998), is the problem of collecting enough observations to obtain stable estimates of RT during the early stages of learning, as performance tends to improve rapidly when people receive corrective feedback. Consequently, studies investigating categorization RTs have often focused on asymptotic performance after the relationships between stimuli and category outcomes have been learned. Given the lack of detailed RT data during the learning process itself, it is somewhat unclear whether error-driven learning mechanisms can account for changes in RTs that might arise during this time. A complete account of category learning performance requires a model that can, at minimum, (1) produce appropriate learning curves that reflect changes in the rates at which different stimuli are assigned to different category outcomes, (2) characterize changes in the time course of decisions resulting in assignment of each stimulus to different category outcomes, and (3) show that the changes in the rates of different categorization responses are commensurate with the changes in RT for those responses during learning.

The discussion so far has identified two theoretical approaches to studying the effects of learning on performance, one based on exemplar-retrieval theories (e.g., instance theory and the EBRW model) and another based on associative learning theories (e.g., ALCOVE). Because the different approaches emphasize different facets of performance, their limitations are complementary: Exemplar-retrieval perspectives tend to emphasize changes in RT more so than accuracy, whereas associative learning perspectives tend to emphasize changes in accuracy over RT. The goal of the current article is to address these limitations by establishing whether an error-driven learning process can simultaneously account for changes in choice probabilities as well as detailed RT distribution data over the course of learning, and whether relating these two facets of performance requires additional theoretical assumptions. In doing so, we seek to strengthen the existing theoretical connections between these frameworks. We structure the rest of the article as follows. First, we introduce a probabilistic category learning task that permits collection of detailed RT distribution data at the level of individual stimuli over the entire course of learning, overcoming the principal challenge to studying RT dynamics during early learning. We argue that probabilistic learning environments are ideal for testing associative learning models against RT data because they produce patterns of behavior that happen to impose strong constraints on models of choice RT. We then describe the diffusion model of Ratcliff (1978; Ratcliff & McKoon, 2008), discussing how a key parameter of the model—namely, the drift rate of the diffusion process—can be linked conceptually with associations relating cues to different category outcomes. We then briefly review recent work that has used choice-RT models to investigate learning dynamics. After presenting our experiment and summarizing the main empirical results, we conduct a diffusion model analysis of our data to determine the extent to which changes in associative strength are responsible for driving changes in categorization performance during learning. We then develop a model that uses an ALCOVE-inspired associative learning model as a front end to drive a diffusion decision model, and test this integrated model against our data. We conclude the article by discussing directions for future research and possible theoretical extensions of the new model.

Probabilistic category learning

In probabilistic category learning tasks, the mapping relating cues to different category outcomes is not deterministic, meaning that the same stimulus, presented on different trials, will not always be assigned to the same category outcome. This endows the task with several desirable properties for studying learning. First, the consistency of the feedback for each individual stimulus is under strict experimental control. For any number of individual stimuli, the probability with which they are assigned to different category outcomes is determined by the experimenter. This means that both the modal category outcome as well as the consistency of the feedback can be varied on an item-by-item basis. If the stimuli are highly discriminable and nonconfusable with one another, then changes in the way people respond to individual stimuli can be unambiguously attributed to the information provided by trial-by-trial feedback. In this way, probabilistic categorization provides an ideal setting for studying the underlying learning process. The second important property about probabilistic categorization tasks is that participants tend to respond in a way that deviates from what would be expected from an optimal response policy. Historically, people’s performance has been described in terms of probability matching, where cues are assigned to different category outcomes at a rate that approximates the relative probabilities of the different category outcomes. For example, if a cue is paired with Category A feedback on 80% of trials and Category B feedback on the remaining 20% of trials, people will tend to assign the cue to Category A 80% of the time and to Category B 20% of the time. This can be contrasted with an optimal maximizing strategy. Under maximizing, a stimulus is always assigned to Category A if the probability of Category A feedback is greater than 0.5; otherwise, the stimulus is assigned to Category B. In reality, neither probability matching nor maximizing provides a completely accurate picture of performance, as people tend to “overshoot” the feedback probabilities while not strictly maximizing either (e.g., Friedman & Massaro, 1998; Nosofsky & Stanton, 2005; Shanks, Tunney, & McCarthy, 2002). The tendency to overshoot, but not maximize, persists even in highly practiced individuals (Edwards, 1961; Sewell et al., 2018); learners are expected to assign stimuli to multiple category outcomes across all stages of learning. The variability in people’s responding permits collection of RT distribution data for both frequently and infrequently reinforced category outcome responses for different stimuli. This imposes strong constraints on models, which must account for the changes in both the proportion of each kind of categorization response and how the shapes of the underlying RT distributions for those responses change with learning (cf. Ratcliff & Rouder, 1998).

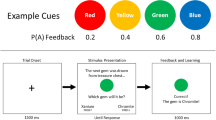
A further benefit of using a probabilistic category learning task is that it allows the same logical task structure to be repeatedly presented to the learner. This overcomes the practical challenge of measuring early leaning RTs identified by Maddox et al. (1998), as it enables collection of a large number of observations at each stage of learning, permitting stable measurement of detailed RT distribution data. For concreteness, consider a set of four highly discriminable cues (e.g., red, yellow, green, and blue color patches; see Fig. 1). Each cue is paired with a unique feedback probability, which determines the relative frequency with which the cue is paired with a Category A or Category B outcome during learning. In tasks using a small number of nonconfusable cues, performance typically stabilizes after each cue has been presented around 30–40 times (e.g., Craig, Lewandowsky, & Little, 2011; Sewell et al., 2018). Because learning proceeds rapidly, it is possible for people to complete multiple runs through the learning task within a single experimental session. Each run through the task comprises a fixed number of trials—enough to ensure that learning is achieved and performance stabilizes—where the mapping between cues and outcomes is randomly determined. Across different runs, the mapping between cues and outcomes can be rerandomized, or an entirely new set of perceptual cues can be introduced. To avoid interference effects, participants are explicitly informed when each run begins and ends. Participants are therefore aware of when new cue–outcome contingencies need to be learned and previously learned information is no longer applicable (cf. Craig et al., 2011; Kruschke, 1996). By repeatedly resetting the learning environment in this way, participants are forced to learn the mappings between cues and outcomes anew for each run. Combining observations across runs result in a large number of observations at the level of individual stimuli during each stage of learning. These data can be used to measure changes in the shapes of RT distributions for different category responses. We adopt this method of repeated task presentation in the current study.

Fig. 1

Illustration of the randomized mapping between discrete cues and feedback probabilities across different runs of a learning experiment. For each run of the task, a set of Category A feedback probabilities are randomly assigned to a set of cues. The feedback probability determines how frequently a cue will be paired with Category A feedback during learning. Because each run involves the same set of feedback probabilities, the logical structure of the learning environment is repeatedly presented. However, learning must begin anew in each run because different perceptual cues appear in each run. This allows data from different runs to be combined, permitting analysis of RT distribution data at the level of individual stimuli, defined by their feedback probability, in each learning block

Diffusion model

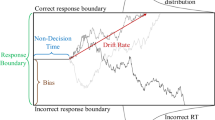
The diffusion model (Ratcliff, 1978; Ratcliff & McKoon, 2008) is a member of the class of sequential sampling models of two-choice decision-making and is among the most rigorously tested in cognitive psychology (Ratcliff & Smith, 2004; Sewell & Smith, 2016). The model conceptualizes decision-making as a noisy evidence accumulation process and decomposes empirical RTs into two components: One that reflects the time course of decision-making and another that summarizes the time required for other processes not involved in decision-making (e.g., stimulus encoding and response execution). According to the model, decisions are made by repeatedly sampling stimulus information and accumulating that information through time. Evidence accumulation begins at some point z, which is situated between two decision boundaries, located at a and 0. Each sample provides some quantity of evidence favoring one of the response alternatives over the other, moving the accumulated evidence total toward one of the two decision boundaries. Once a sufficient quantity of evidence has been accumulated and the process reaches a decision boundary, the corresponding behavioral response is initiated. Figure 2 provides a schematic illustration of the model.

Fig. 2

Schematic illustration of the diffusion model. Empirical RTs are the sum of two independent components. The first summarizes the time course of the decision process; the second summarizes the time course of processes not related to decision-making (e.g., stimulus encoding and response execution). Decisions are the product of noisy accumulation of stimulus information. The rate of evidence accumulation is controlled by the drift rate of the diffusion process, which reflects the quality of information entering the decision process. The time course of decision-making is jointly determined by the drift rate and the evidence threshold set by the individual. Higher drift rates lead to faster and more accurate decisions, whereas a higher decision threshold results in slower but more accurate decisions. The time course of other processing stages not related to decision-making is summarized by the nondecision time parameter

In the diffusion model, the time course of decision-making is determined jointly by the quality of the information provided by the stimulus, which controls the rate of evidence accumulation, and the decision threshold, which determines how much evidence is required before a choice is made. The former is reflected in the drift rate of the diffusion process (v), which indexes the quality of information driving decision-making. When the drift rate is high, decisions will be faster and more accurate; when the drift rate is low, decisions will be slower and more prone to error. The decision threshold is controlled by the boundary separation parameter (a). High values reflect cautious decision-making, resulting in slow but accurate responses; low values reflect a greater emphasis on response speed, resulting in faster responses but more errors. The time course of encoding and response processes not related to decision-making is summarized by the nondecision time parameter (T_er). The diffusion model allows drift rate and nondecision time to vary on a trial-by-trial basis, reflecting the presence of noise in the processes involved in stimulus representation (η, capturing drift variability) and variability in the efficiency of encoding and response processes (s_t, capturing nondecision time variability; see Ratcliff, 2013, for further discussion about parameter variability across trials).

The diffusion model has accounted for a wide range of data at the level of choice probabilities and the shapes of RT distributions for correct and error responses (see Ratcliff, Smith, Brown, & McKoon, 2016, for a recent review). Due to its success in accounting for data at this fine-grained level of analysis, the model is often used in a measurement capacity as a meeting point between theory and data. Diffusion model analysis permits identification of experimental factors that affect specific aspects of the decision process. Typically, differences in drift rates are of most theoretical interest, as these reflect differences in the quality of information used to make decisions across experimental conditions. While a pure diffusion model analysis suffices to identify which aspects of the decision process differ across conditions, it does not explain how those differences came to be. Ideally, the changes in drift rates—or any other parameters that are required to vary across conditions in order to account for data—would be explained by a psychological theory of the representational processes that support decision-making. With respect to probabilistic category learning, we are interested in how association-based representations support category learning, and how learning processes that modify these associations incrementally adjust the drift rates that determine choice behavior. The EBRW model of Nosofsky and Palmeri (1997a, 2015) is one way of relating category representations to a decision process, which relies on the race model assumptions that define memory retrieval in Logan’s (1988) instance theory to explain changes in RT. Here, we investigate a complementary theoretical approach that explores the adequacy of using learned association-based representations to produce changes in both choice and RT data simultaneously. A key question is whether speed-ups in RT can also be explained in terms of changes in associative strength. Showing that an associative framework can account for combined choice-RT data sets the stage for future research to more directly compare association-based theories with exemplar-retrieval theories.

Relating learning and decision-making with the diffusion model

In the context of category learning theories (e.g., Kruschke, 1992; Love et al., 2004), relative support for different category responses is indexed by the strength of associations relating the stimulus to different category outcomes. Conceptually, drift rates in the diffusion model index the same kind of information (i.e., relative support for different decision outcomes, given the stimulus), and so it is straightforward to identify changes in drift rates in learning tasks with changes in relative associative strength. The idea that associative learning enhances drift rates has found support from several studies that have used the diffusion model to investigate learning effects. For example, Petrov, Van Horn, and Ratcliff (2011) observed systematic increases in drift rates across trial blocks in a perceptual learning task, reflecting improvements in people’s ability to extract information from a stimulus. Liu and Watanabe (2012) reported similar practice-related changes in a motion discrimination task. Analogous increases in drift rates have been observed in other perceptual discrimination tasks involving brightness and letter stimuli in both older and younger adults (Ratcliff, Thapar, & McKoon, 2006). Practice-related increases in drift rates have also been observed in higher order cognitive tasks, such as lexical decision (Dutilh, Vandekerckhove, Tuerlinckx, & Wagenmakers, 2009), and have been shown to reflect both task-general and stimulus-specific components (Dutilh, Krypotos, & Wagenmakers, 2011; Petrov et al., 2011). Stimulus-specific effects on drift rates are of particular relevance, as these are consistent with learned strengthening of associations between stimulus-representations and response outcomes.

Recent work by Frank and colleagues has provided a more detailed investigation of trial-by-trial learning effects on decision-making. Much of this work has used a reward learning paradigm that is different from probabilistic category learning, but shares many important characteristics. In their probabilistic selection task (Frank, Seeberger, & O’Reilly, 2004), participants are presented with pairs of stimuli that each have unique probabilities of being associated with a reward. On each trial, participants must choose one of the two presented stimuli and are rewarded according to the probability associated with the chosen stimulus. The task is well suited for examining choice under uncertainty. Depending on the stimuli presented on a given trial, decisions can vary in terms of whether a reward is more or less likely (e.g., by presenting two stimuli with reward probabilities both greater than or less than 0.5), and the level of conflict created by the choice alternatives (e.g., when both stimuli have similar reward probabilities, conflict is higher than when the presented stimuli have divergent reward probabilities). Ratcliff and Frank (2012) investigated the relationship between a neurally inspired reinforcement learning model (Frank, 2005, 2006) and the diffusion model via simulation. They found that data simulated by the learning model could be accommodated by a version of the diffusion model that allowed time-dependent decision boundaries for high-conflict trials as well as one that introduced a delayed decision onset for the high conflict trials with an unlikely reward outcome.

Pedersen, Frank, and Biele (2017) extended the work of Ratcliff and Frank (2012) by combining a reinforcement learning model with the diffusion model to account for changes in choice behavior of adults with attention-deficit/hyperactivity disorder in the probabilistic selection task. Pedersen et al. showed that a model that incorporated collapsing decision boundaries across trials as well as differential learning rates for correct and error trials was needed to completely account for performance of participants on and off medication. Taken together, the results of Pedersen et al. and Ratcliff and Frank highlight how the theoretical assumptions of learning models are quite compatible with decision models such as the diffusion model. A limitation of those studies, though, is that the nature of the experimental designs precluded a detailed examination of the changes in RT distribution data over the course of learning. We seek to overcome this limitation via repeated presentation of the logical task structure.

More closely related to the current work is a recent study by Frank et al. (2015), who used a probabilistic reward learning task involving presentation of only a single stimulus per trial. In this task, people learned to select a rewarded response alternative for each of three unique stimuli via trial-and-error learning. Frank et al. applied the diffusion model to the trial-by-trial learning data covering 40 presentations of each stimulus. Drift rates were related to the difference in expected value for choosing each response alternative, given the stimulus. Model parameters were further constrained by trial-by-trial electroencephalogram (EEG) and functional magnetic resonance imaging (fMRI) data. Frank et al. showed that combining a reinforcement learning model with the diffusion model produced good fits to the learning data, and that trial-by-trial variation in decision threshold could be predicted by variation in both EEG and fMRI signals.

The recent work reviewed above shows that changes in choice behavior can be explained in terms of systematic changes in diffusion model parameters as a function of learning. There is particularly strong support for increases in drift rate as a function of practice (e.g., Dutilh et al., 2009; Liu & Watanabe, 2012; Ratcliff et al., 2006). Importantly, these learning effects can at least partially be attributed to stimulus-specific learning effects, which imply a role for associative learning mechanisms (e.g., Dutilh et al., 2011; Petrov et al., 2011). More recent analyses of trial-by-trial learning performance have further shown that error-driven reinforcement learning models provide a good process account for how drift rates evolve over the course of learning (Frank et al., 2015; Pedersen, et al., 2017). However, changes in performance may not be solely driven by changes in drift rates, as reduced decision thresholds have often been observed during learning (Dutilh et al., 2011; Dutilh et al., 2009; Liu & Watanabe, 2012; Pedersen et al., 2017; Petrov et al., 2011; Ratcliff & Frank, 2012). The relative contributions of changes in drift rates and decision thresholds to changes in learning performance can only be clearly identified via detailed model-based analysis of changes in choice-RT distribution data.

Overview of the current study

In the current study, we seek to determine the extent to which changes in categorization performance are driven by learning-related changes in drift rates, and whether changes in other decision parameters are needed to account for the data. To ensure that sufficient observations are collected to reliably estimate RT distributions for different response alternatives for stimuli in each learning block, we have participants complete multiple sessions of a probabilistic category learning task. Each session of the experiment presents three different runs through the learning task (i.e., the same set of feedback probabilities are used, but the perceptual cues that define the stimuli differ across each run within a testing session).

To identify which aspects of the decision process are affected by learning, we conduct a diffusion model analysis of the complete set of choice-RT data. We report nested model comparisons to identify which parameters of the diffusion model are required to vary across stimuli and learning blocks in order to account for the data. After identifying the version of the diffusion model that provides the best balance between fit and parsimony, we develop a new model that combines a front-end associative learning model that uses a standard error-driven learning rule to adjust association weights relating cues to different category outcomes. We show that relating associative strengths to drift rates using an adaptation of Luce’s (1959) choice rule successfully produces changes in drift rates that allow the model to account for learning data. We show that the fit of this integrated category learning model is comparable with that of the best performing diffusion model, and is simpler in terms of the number of freely estimated parameters. The success of the model shows that changes in drift rates required to account for detailed choice-RT distribution data in a simple probabilistic learning task can be predicted by a standard error-driven associative learning rule. The model provides a complete account of the data from this task, and given its relationship to established exemplar models of category learning, can potentially be extended to more complex tasks involving multidimensional stimuli with variable interitem similarity.

Materials and methods

Participants

Six participants (five female) from the University of Melbourne were recruited for the experiment. One participant was excluded from the study after the first session, due to failing to understand the task and responding randomly. The final sample comprised five females between the ages of 19 and 30 years (M = 24.4, SD = 3.97), each of whom completed six sessions of testing. Each session lasted approximately 40 minutes. Participants were remunerated A$12 per session.

Apparatus

The experiment was programmed in MATLAB, using the Psychophysics Toolbox (Brainard, 1997; Pelli, 1997), and was run on a Windows PC. Responses were collected using a Cedrus RB-540 response box.

Design and stimuli

Each participant completed six sessions of a probabilistic category learning task. Separate sessions were scheduled on different days, at the convenience of the participants. Each session was divided into three separate runs. The runs were functionally identical copies of a five-block learning task. Runs differed in terms of the perceptual cues that defined the stimuli, thereby avoiding interference from prior learning, and requiring cue–outcome contingencies to be learned anew. Within each run, people had to learn the probabilistic associations between four discrete-valued stimuli and two category outcomes via trial-by-trial feedback. The Category A outcome probabilities were 0.20, 0.40, 0.60, and 0.80. The three stimulus sets used in the experiment are shown in Fig. 1 and consisted of color patches (red, yellow, green, and blue), mathematical symbols (plus, minus, divide, and multiply), and card suits (hearts, clubs, diamonds, and spades). For each participant, in each session, the order in which people encountered the different stimulus sets was randomly determined. Within each run, the mapping of individual stimuli to category outcome probabilities was determined randomly. Having participants complete three runs through a short learning experiment across multiple testing sessions allowed us to aggregate data across runs and testing sessions, permitting analysis of data at the level of RT distributions for both Category A and Category B responses for each stimulus, in each of the five learning blocks. This fine-grained level of analysis is essential for developing and testing models that can address changes in choice-RT data over the course of learning.

Pilot testing was conducted to ensure that stimuli in each of the three sets were nonconfusable. This involved a series of identification studies, where participants had to identify each stimulus as quickly as possible while maintaining accuracy. Of the many stimulus sets we considered, the three shown in Fig. 1 produced comparable mean identification RTs and similar encoding latencies as indexed by the leading edge of the identification RT distributions (e.g., Ratcliff & Smith, 2010; Smith, Ratcliff, & Sewell, 2014). Given the distinctiveness of the individual stimuli, identification errors were extremely rare.

Procedure

Participants completed each session individually in a quiet testing booth. At the start of the first experimental session, participants were presented with a cover story introducing the task. Participants adopted the role of a treasure hunter exploring a cave that contained four treasure chests, identified by the different stimuli. Participants were instructed that each treasure chest contained a mixture of two types of fictitious gems (Chromite and Xanium), and on each trial, a single gem was extracted from one of the treasure chests. Participants were required to guess which type of gem was extracted on each trial. If they guessed correctly, they got to keep the gem; otherwise, it was destroyed. Participants were encouraged to make as many correct responses as possible, and were told that they could use the feedback they received to help determine which gem was more likely to be found in each treasure chest. Participants were also informed that the relationships between the stimuli and the category outcomes were randomly determined for each run and each session. Before beginning the task, participants were able to ask any questions about the task instructions.

For each session, before the start of each experimental run, participants were shown the complete set of stimuli that would be used in that run. Participants then began the category learning task. Each trial began with the presentation of a central fixation dot for 800 ms. One of the four stimuli being used in the run was then presented centrally until a category response was made. Participants responded by pressing either the left (Category A) or right (Category B) button of the response box. Immediately following a response, participants were presented with feedback indicating the correct category outcome for that trial. Feedback was presented directly beneath the stimulus and remained on-screen for a study period of 1,000 ms. To encourage timely responding on the task, trials with RTs slower than 2,000 ms resulted in additional speed feedback being presented. The speed feedback, “TOO SLOW!!,” was presented for 3,000 ms after the category outcome feedback was extinguished (i.e., the study period was always limited to 1,000 ms). Once all feedback had been presented, there was an 800 ms blank intertrial interval. The next trial began immediately afterwards. Figure 3 shows an example trial sequence.

Fig. 3

Time course of events during an individual learning trial. All trials began with the presentation of a central fixation dot for 800 ms. The stimulus was then presented centrally along with category response options underneath. The stimulus remained on-screen until the participant made a response, after which category outcome feedback was immediately presented. Feedback appeared underneath the stimulus, reporting whether the response was correct or incorrect and the correct category outcome label. This information remained on-screen for a study period of 1,000 ms. For trials where a response was slower than 2000 ms, the feedback screen was followed by an otherwise blank screen displaying “TOO SLOW!!” for 3,000 ms. Each trial ended with an 800 ms blank intertrial interval

In each run of the experiment, participants completed five blocks of learning trials. Within each block, the four stimuli were presented 10 times each, resulting in 200 learning trials per run. Participants had the opportunity to take self-paced breaks after every 20 trials. Upon completion of the first run, participants were able to take a self-paced break before viewing the stimulus set to be used in the next run. Stimulus presentation order was determined randomly for each participant in each run of each session.

Results

For each participant, data from all six sessions were combined, resulting in a total of 3,600 trials per participant. This resulted in 180 observations per stimulus, per learning block, providing ample trials for estimating the shapes of RT distributions for both Category A and Category B responses. We present our analysis in three parts. In the first part, we present changes in response probabilities and mean RT over the course of the five learning blocks. In the second part, we report a model-based analysis of the group-averaged data using Ratcliff’s (1978; Ratcliff & McKoon, 2008) diffusion model. In the third part, we develop a model that combines error-driven associative learning principles with a sequential sampling decision mechanism, showing that the model is able to learn the pattern of drift rates identified by the diffusion model analysis, and provide an accurate and parsimonious account of the complete set of learning data.

Data screening

The diffusion model provides an account of “one-shot” decisions, where choice behavior is determined by a single-stage decision process. To avoid incorporating trials where other kinds of decision procedures may have been applied—such as more complex multi-stage decisions or responses based on fast anticipatory responses—we sought to remove trials that produced unusually fast or slow RTs. To this end, we screened out responses that had RTs faster than 200 ms, as these were likely to have been prepared prior to stimulus onset. We also removed trials that were slower than 2,000 ms, as these were trials that elicited “Too Slow” feedback during the task, and may have involved lapses of attention or application of idiosyncratic and more complex decision strategies. Out of a total of 18,000 trials, these criteria removed 2.3% of the total data set.

Empirical results

We first provide a summary of the data by analyzing group-averaged choice probability and mean RT data. These analyses serve to illustrate the major trends in the learning data, showing that our method of repeatedly testing individuals across multiple sessions produced data that are highly representative of results commonly produced by single-session probabilistic category learning studies.

Choice probability

Choice probabilities for the four stimuli—defined by the four levels of Category A feedback: 0.2, 0.4, 0.6, and 0.8—across the five learning blocks are shown in Fig. 4. The largest changes in choice probabilities occur between the first and second learning blocks, after which they remain relatively stable. Asymptotically, participants tend to assign stimuli to the different outcome categories in a way that overshoots the feedback probabilities while also not maximizing. For each stimulus, the average choice probability is more extreme than the feedback probability associated with that stimulus. This overshooting behavior is typical of responding under probabilistic feedback (e.g., Craig et al., 2011; Nosofsky & Stanton, 2005; Sewell et al., 2018; Shanks et al., 2002). Visual inspection of the individual response profiles confirmed that all participants exhibited the same probability matching behavior, responding similarly to each stimulus over the entire course of learning. This allays concerns that the pattern of responding we observe here is due to combining data from participants whose probability matched with other participants who employed a strict maximizing strategy (i.e., always responding Category A when the probability of Category A feedback was greater than 0.5, otherwise, responding Category B).

Fig. 4

Choice probabilities, quantified as the proportion of Category A responses, averaged across participants for each learning block. Each line summarizes responding to a different stimulus, defined by its feedback probability (i.e., the proportion of trials the stimulus was paired with Category A feedback, which was either 0.2, 0.4, 0.6, or 0.8). Data for stimuli with more consistent feedback (i.e., the 0.2 and 0.8 stimuli) are plotted with circles. Data for stimuli with less consistent feedback (i.e., the 0.4 and 0.6 stimuli) are plotted with squares. Open symbols denote stimuli that were paired with Category A feedback on fewer than 50% of trials. Participants tended to overshoot the feedback probabilities, in line with existing literature. Error bars show the standard error of the mean

To provide statistical confirmation of learning, we conducted a 4 (stimulus, indexed by the four levels of Category A feedback: 0.2, 0.4, 0.6, and 0.8) × 5 (learning block) repeated-measures ANOVA on the choice probability data. The analysis revealed a significant main effect of stimulus, F(3, 12) = 117.72, MS_e = .024, p < .001, η_p² = .97, reflecting the different rates at which people assigned the four stimuli to Category A. There was also a significant interaction between stimulus and learning block, F(12, 48) = 10.05, MS_e = .121, p < .001, η_p² = .72, indicating the tendency for people to assign the 0.6 and 0.8 stimuli to Category A at an increasing rate across blocks, and to assign the 0.2 and 0.4 stimuli to Category A at a decreasing rate across blocks. The main effect of learning block was not significant, indicating the absence of any general response bias favoring one category response over another, F(4, 16) = 0.23, MS_e = .04, p = .92.

Mean response time

Figure 5 shows mean RTs for each of the four stimuli across the five learning blocks. The figure shows a reduction in RT for all stimuli across learning blocks, suggesting a modest practice effect. It also appears that RTs for stimuli paired with more consistent feedback (i.e., the 0.2 and 0.8 stimuli, plotted in the figure using circles) are faster than those for stimuli with less consistent feedback (i.e., the 0.4 and 0.6 stimuli, which are plotted in the figure using squares). We investigated these differences via a 4 (stimulus, indexed by the four levels of Category A feedback: 0.2, 0.4, 0.6, and 0.8) × 5 (learning block) repeated-measures ANOVA. There was a main effect of stimulus, F(3, 12) = 5.48, MS_e = .002, p = .013, η_p² = .58, reflecting a RT advantage for stimuli with more consistent feedback. There was also a main effect of learning block, F(4, 16) = 3.86, MS_e = .002, p = .022, η_p² = .49, reflecting a 45-ms reduction in mean RT from the first learning block, M = 619 ms, to the last learning block, M = 574 ms. The interaction was not significant, F(12, 48) = 0.79, MS_e < .001, p = .66.

Fig. 5

Mean RTs averaged across participants for each learning block. Each line summarizes responding to a different stimulus, defined by its feedback probability (i.e., the proportion of trials the stimulus was paired with Category A feedback, which was either 0.2, 0.4, 0.6, or 0.8). For all stimuli, there were reductions in RT across learning blocks, consistent with practice effects. Data for stimuli with more consistent feedback (i.e., the 0.2 and 0.8 stimuli) are plotted with circles. Data for stimuli with less consistent feedback (i.e., the 0.4 and 0.6 stimuli) are plotted with squares. Open symbols denote stimuli that were paired with Category A feedback on fewer than 50% of trials. Error bars are the standard error of the mean

Summary of empirical results

Taken together, the pattern of results from our multisession probabilistic category learning experiment is consistent with results typically found in single-session studies. Participants in our study responded by overshooting the feedback probabilities, as is commonly found in the literature. Mean RTs were shown to be sensitive to how diagnostic feedback was. Stimuli with more consistent feedback (i.e., Category A feedback probabilities closer to 1 or 0) were, on average, responded to faster than stimuli with less consistent feedback. We also observed practice effects in the mean RT data. These effects, although relatively small, are striking given the high level of experience people had with the task (i.e., completion of 18 runs through a learning task involving the same set of feedback probabilities throughout). We now present more detailed model-based analyses of the choice-RT data, which seek to simultaneously characterize the changes in choice probabilities and RTs observed over the course of learning.

Diffusion model analysis of learning

The analyses reported above reveal two hallmarks of learning in our data: choice probabilities that adaptively change in light of feedback and progressively faster RTs with increasing task experience. Those traditional analyses, however, only provide limited insight into performance, as they do not address more detailed RT distribution data for different types of category responses, or how these data are affected by learning. More importantly, those analyses are not able to address whether the changes in choice probabilities are commensurate with the observed changes in RTs. That is, can a single learning mechanism jointly explain both facets of performance simultaneously? To address this, we conducted a diffusion model analysis of the learning data. The goal of this analysis is to determine whether the changes in performance we observed can be attributed to variation in a single model parameter—implying a singular mechanistic locus of learning—or if multiple parameters are required to account for changes in performance. If changes in drift rates suffice to explain learning-related changes in performance, this would strongly imply that the learning effects in our data can be attributed to learned changes in associative strengths relating cues to category outcomes.

Response time quantile data

To fit the diffusion model to the data, we summarized each individual’s RT distribution data for Category A and Category B responses for each stimulus in each learning block. Following convention, empirical RT distributions were summarized using the 0.1, 0.3, 0.5, 0.7, and 0.9 RT quantiles (Ratcliff & Smith, 2004). The individual RT distribution data were then averaged across participants to obtain quantile averaged data, which were fit by the diffusion model. Before presenting the model fits, we discuss some of the regularities in the RT distribution data and describe the method of presenting these data.

In this article, RT quantile data are shown using modified quantile probability plots (see Fig. 6; cf. Ratcliff & Smith, 2004). In these figures, RT quantiles for Category A and Category B responses are plotted against their respective choice probabilities for each stimulus in each learning block. Each panel of Fig. 6 depicts changes in choice probabilities and the shapes of the Category A and Category B RT distributions across the five learning blocks for a single stimulus. The numerical plotting symbols in each panel identify performance from the corresponding learning block. For each learning block, there are two columns of plotting symbols: one that summarizes the shape of the Category A RT distribution, and another that summarizes the shape of the Category B RT distribution. For each column of plotting symbols, moving upwards along the ordinate, the plotting symbols identify the 0.1, 0.3, 0.5, 0.7, and 0.9 RT quantiles for the relevant category response. The relative spacing between successive plotting symbols summarizes the shape of the corresponding RT distribution, reflecting how far apart successive RT quantiles are along the time axis. The position of each column along the abscissa reflects the probability of each category response within a learning block. Empirically, category responses that match the modal category outcome for each stimulus are more common than those that do not match the modal category response. To facilitate visual comparison of performance across different stimuli, we plot category responses that match the modal feedback outcome for that stimulus on the right-hand side of each panel. Category responses that do not match the modal feedback outcome for a given stimulus are plotted on the left-hand side of each panel. For example, for the P(A) = 0.2 stimulus, shown in the top left panel of Fig. 6, Category B responses are shown on the right-hand side of the figure, whereas Category A responses are shown on the left-hand side of the figure. For the P(A) = 0.8 stimulus, shown in the bottom right panel of the figure, the reverse is true. Given the probabilistic nature of feedback, responses on the right-hand and left-hand side of each panel can be viewed, in a normative sense, as corresponding to “correct” and “error” responses, respectively. For ease of communication, we use these terms to describe responses people make to different stimuli.

Fig. 6

Modified quantile probability plot (QPP) for showing changes in the shapes of categorization RT distributions over the course of learning. Each panel in the figure shows response data for a different stimulus, as defined by its feedback probability. Data from each of the five learning blocks are indexed by the numerical plotting symbols. Responses that match the modal category outcome for each stimulus are displayed on the right-hand side of each panel, and are, in a normative sense, “correct” responses. Responses that do not match the modal category outcome for each stimulus are displayed on the left-hand side of each panel, and are, in a normative sense, “error” responses. Choice data from each block are therefore presented in two columns. The location of each column of data along the abscissa corresponds to the probability of each category responses. For example, for the P(A) = 0.8 stimulus, Category A responses in the first block are shown as the column of 1s on the right-hand side of the lower right panel in the figure. This shows that approximately 75% of responses to this stimulus, in the first learning block, were Category A responses. Category B responses in the first block are shown as the columns of 1s on the left-hand side of the same panel (i.e., approximately 25% of responses to this stimulus, in the first learning block, were Category B responses). Within each column of data, the five plotting symbols indicate, ascending upwards along the ordinate, the 0.1, 0.3, 0.5, 0.7, and 0.9 RT quantiles for the relevant category response. The relative spacing of plotting symbols within each column describes the shape of the corresponding RT distribution for the relevant category response in each learning block

One of the striking regularities in the RT quantile data is that correct responses appear consistently faster than error responses. This pattern is common in perceptual tasks that emphasize accuracy rather than speed (e.g., Luce, 1986; Swensson, 1972) and is consistent with our task instructions, which encouraged participants to maximize the proportion of correct responses. To gain a clearer picture about how stable this pattern of RT differences was, we conducted a regression analysis predicting the mean difference in RT quantiles (i.e., error RT minus correct RT) as a function of whether the stimulus was a strong or weak predictor of category outcome—that is, the P(A) = 0.2 and P(A) = 0.8 stimuli versus. the P(A) = 0.4 and P(A) = 0.6 stimuli—learning block, and RT quantile. These differences in the RT quantiles are shown in Fig. 7. The analysis showed that the RT difference for correct versus error responses was larger for strongly predictive stimuli compared with weakly predictive stimuli, β = 0.36, p < .001, increased as a function of RT quantile, β = 0.52, p < .001, but maintained a consistent size across learning blocks, β = −0.07, p = .36. These features of the RT distribution data suggest that feedback probability introduces an asymmetry in the speed with which different category responses are made, with more consistent feedback resulting in a greater RT advantage for the correct, more frequently occurring, category outcome. Differences in the shapes of the underlying RT distributions for correct and error responses are underscored by tail quantiles exhibiting a larger RT advantage for correct responses. Interestingly, the lack of any predictive effect of learning block suggests that the RT advantage for correct responses is not eliminated even in highly practiced participants, such as the ones in our study.

Fig. 7

Group averaged difference in RTs (error RT – correct RT) for different distribution quantiles in each learning block. The two panels show the RT difference for data averaged across strongly predictive stimuli—that is,, P(A) = 0.2 and P(A) = 0.8—and weakly predictive stimuli—that is, P(A) = 0.4 and P(A) = 0.6—in the left and right panels, respectively. The difference in RTs gets larger in the tails of the RT distributions as error RT quantiles become progressively slower than the corresponding correct RT quantiles, reflected by the upward trend in the data. The effect is more pronounced for strongly predictive stimuli

Model-fitting procedure

We now report nested model comparisons to identify a version of the diffusion model that provides the best and most parsimonious account of the choice-RT data. Unless otherwise specified, for the models we tested, the values for boundary separation (a), nondecision time (T_er), and between-trial variability in drift rates (η), and nondecision time (s_t) were held constant across all stimuli and all learning blocks. Drift rates (v) were typically allowed to vary across different stimuli and different learning blocks in order to characterize the effects of associative learning on performance. For all models, we assumed an unbiased decision process, setting the start point of evidence accumulation to z = a/2. For each model we tested, parameters were estimated by minimizing the likelihood ratio statistic, G², defined as

$$ {G}^2=2\sum \limits_{i=1}^{20}{n}_i\sum \limits_{j=1}^{12}{p}_{ij}\ln \left(\frac{p_{ij}}{\pi_{ij}}\right). $$

(1)

In Eq. 1, the outer summation over i indexes the 20 experimental conditions formed by factorial combination of the four stimuli across each of the five learning blocks. The inner summation over j indexes the 12 bins formed by the RT quantiles for Category A and Category B responses in each experimental condition. The p and π terms correspond respectively to the observed and predicted proportions of responses in each bin. The number of trials per condition is described by n, which was equal to 180. Model predictions were computed using the methods described by Tuerlinckx (2004).

Fixed drift rate model

To establish a baseline level of fit, we first considered a version of the diffusion model where drift rates for each of the four stimuli were fixed across the five learning blocks. Although this model cannot predict learning-related changes in performance, it is useful because it provides a way of quantifying the benefits of associative learning, which we discuss later on. To reduce the total number of free parameters that were estimated, drift rates for the two strongly predictive stimuli—that is, the P(A) = 0.2 and P(A) = 0.8 stimuli—were constrained to have equal values, but opposite signs.² The same restriction was applied for the two weakly predictive stimuli—that is, the P(A) = 0.4 and P(A) = 0.6 stimuli. The baseline model therefore required six free parameters, two drift rates (v_Strong and v_Weak), the boundary separation parameter (a), nondecision time (T_er), and between-trial variability parameters for drift rate and nondecision time (η and s_t, respectively). Due to the lack of any way to account for learning effects across trial blocks, the fit of the baseline model was quite poor, G²(214) = 126.03, and we do not show the predictions of this model against data.

Variable drift rate models

To examine the effects of associative learning on performance, we considered two alternatives to the baseline model that allowed drift rates to vary across learning blocks.³ We first considered a constrained model where changes in drift rates across learning blocks for strongly and weakly predictive stimuli were controlled by separate functions, each describing an exponential approach to a limit,

$$ {v}_i={v}_{\mathrm{Max}}\left(1-\exp \left(- ci\right)\right). $$

(2)

In Eq. 2, the drift rate in learning block i, v_i, is determined by the asymptotic drift rate, v_Max, and an exponential rate parameter, c. As with the baseline model, drift rates for the two strongly predictive stimuli were constrained to have equal values, but opposite signs. The same was true for the two weakly predictive stimuli. This exponential model required two additional free parameters relative to the baseline model (i.e., two asymptotic drift rates and two exponential rate parameters replacing the two fixed drift rates of the baseline model), and provided a significantly better fit to the data, ΔG²(2) = 56.62, p < .001. In an absolute sense, the fit of the exponential model was quite good, G²(212) = 69.41, and is shown in Fig. 8. Best fitting parameter estimates for the exponential model are shown in Table 1.

Fig. 8

Fit of the exponential model to the data. Data are the same as in Fig. 6. Diffusion model predictions are plotted as open circles connected by solid lines. Different lines connect model predictions for each of the five RT quantiles (e.g., the line that is lowest on the ordinate in the figure corresponds to the predicted 0.1 RT quantile, the line that is highest on the ordinate in the figure corresponds to the predicted 0.9 RT quantile). With drift rates changing according to an exponential function across blocks, the model is successfully able to capture all of the major trends in the data

Table 1 Best fitting parameter estimates for the exponential model

Several comments apply to the fit of the exponential model. First, the model successfully describes the changes in choice probabilities for the four stimuli across learning blocks. In particular, the model correctly predicts relatively large changes in performance across the first two blocks, followed subsequently by only minor changes in performance across the remaining blocks. Second, the model successfully captures the changes in the shapes of RT distributions for both correct and error responses over the course of learning. Importantly, the model captures the consistent RT advantage for correct responses over errors across all distribution quantiles and all learning blocks. Although there are some deviations between model predictions and data—such as minor misses in accuracy for some of the stimuli and occasional underprediction of error RT quantiles in the first learning block⁴—the success of this relatively simple implementation of the diffusion model is notable. In our view, a successful learning model should be able to explain both relatively rapid early changes in performance that are followed by relatively stable performance. In addition, a successful model should be able to identify the point at which performance stabilizes. The exponential model is able to explain both of these facets of performance. In providing a close fit to the data, the model supports the idea that the associative learning process can be viewed as describing changes in drift rates driving decision-making.

Despite the convergence of predictions from the exponential model with the learning data, it is possible that a different set of theoretical assumptions could achieve a better fit. To get a sense of what an upper limit of good fit to our data would look like within a diffusion model framework, we also considered a more flexible implementation of the model. Unlike the exponential model, this flexible model does not impose any regularity upon block-by-block changes in drift rates. Instead, drift rates for strong and weakly predictive stimuli are freely estimated from the data for each learning block. Once again, drift rates for the strongly and weakly predictive pairs of stimuli were constrained to have equal values but opposite signs (i.e., a total of 10 drift rates were freely estimated from the data). Removing the exponential constraint on changes in drift rates resulted in an additional six free parameters being estimated from the data, compared to the exponential model. The additional flexibility—nearly doubling the number of free parameters in the model—did little to improve the quality of fit above that of the exponential model, ΔG²(6) = 5.53, p = .48. On balance then, we conclude that the fit of the exponential model provides as good a fit to the learning data as can reasonably be expected from the diffusion model when drift rate is the only parameter that can change across learning blocks. The exponential model provides a good account of all the major regularities in the data in a parsimonious way, accounting for 220 data degrees of freedom with only eight free parameters.

Alternatives to the exponential model

The success of the exponential model supports the idea that the effects of associative learning can be captured by changes in the drift rate of the diffusion model. This result is consistent with other diffusion model analyses of learning effects (e.g., Frank et al., 2015; Petrov et al., 2011; Ratcliff & Frank, 2012). We next consider whether learning selectively influences drift rates or if other decision parameters are also affected. If selective influence holds, and no other model parameters change across learning blocks, it would highlight compatibility between error-driven models of learning and the sequential sampling framework for modeling decision-making.

We therefore considered two other variations of the diffusion model that were extensions of the exponential model. The first version assumed that, in addition to exponential changes in drift rates across learning blocks, learning also resulted in changes in the nondecision time parameter, T_er. This would be tantamount to assuming increased efficiency in the encoding of stimuli—or potentially in the retrieval of specific cue–outcome associations—as a function of learning. This version of the model was identical to the exponential model, except that nondecision time was estimated on a block-by-block basis. This model failed to produce a significant improvement in fit over the exponential model, ΔG²(4) < 1, as there was little variation in the leading edge of the empirical RT distributions across blocks (i.e., the 0.1 RT quantile was quite consistent across learning blocks for all stimuli; see Fig. 8). The second model we considered was one where boundary separation, a, could change over the course of learning. The idea that people may reduce decision thresholds as they gain experience in a task was shown by Dutilh et al. (2009) in the context of practice effects in lexical decision. These authors observed consistent narrowing of boundary separation across trials (i.e., progressively lower decision thresholds). Although this would normally result in reduced accuracy, the changes in boundary separation were accompanied by increases in drift rates. The combination of these changes served to keep decision accuracy constant, while enabling faster RTs. We implemented a variable threshold model that was analogous to the variable nondecision time model considered above, estimating a unique boundary separation parameter for each learning block. Like the variable nondecision time model, though, the variable threshold model failed to produce a significant improvement in fit over the exponential model, ΔG²(4) < 1. We conclude that the only parameters that were systematically affected by learning were those that determined changes in drift rates.

Summary of diffusion model analysis

Our diffusion model analysis of the learning data strongly supports the idea that learned changes in associative strength can be successfully modeled as changes in the drift rate of the diffusion model. Specifically, we found changes in drift rates to be approximately exponential in form, which is consistent with error-driven learning algorithms that are commonly used in the category learning literature (e.g., Kruschke, 1992; Kruschke & Johansen, 1999; Love et al., 2004). During the initial learning blocks, changes in drift rates are relatively large from block to block. However, the changes become progressively smaller as learning proceeds and performance stabilizes. The analysis also showed that learning appeared to selectively influence drift rates. We failed to find any evidence that other model parameters (i.e., boundary separation or nondecision time) were affected by learning. In sum, the diffusion model analysis suggests that learning-related changes in categorization performance are driven solely by changes in drift rate. Because drift rates index relative support for competing category outcomes, their function is analogous to learned associative strengths in traditional category learning models (e.g., Kruschke, 1992; Kruschke & Johansen, 1999; Love et al., 2004). The next question is whether the changes in drift rates that are required to account for the data can be produced within an error-driven framework for modeling category learning.

An integrated model of learning and response time

In this section, we develop a category learning model that relates error-driven changes in associative strengths to changes in the drift rate driving a sequential sampling decision mechanism. The model we develop uses a standard error-driven learning rule to update changes in association weights linking cue representations to different category outcomes. We considered several variations of this model to test different assumptions about how patterns of association weights relate to drift rates. To preview, we find the relationship between learned associations and drift rates to be nonlinear, relying on an implementation of Luce’s (1959) choice rule in order to appropriately capture the dynamics of learning. Without the nonlinear scaling, the model fails to capture the rapid changes in choice probabilities that are observed in the early stages of learning, and prevents performance from stabilizing in the latter part of the task. These results dovetail with the recent analysis of Pedersen et al. (2017), who found support for a nonlinear relationship between drift rates and association strength in a reward prediction task.

Formal description of the learning model

The integrated model of learning and RTs assumes that presentation of a cue activates an exemplar-based representation of that cue in memory. Because our study involved nonconfusable discrete-valued stimuli, for simplicity, we assume that exemplar activation is achieved in an all-or-none way via a Boolean activation function. Formally, when cue i is presented, the activation of exemplar node i is set to ψ_i = 1; otherwise, ψ_i = 0. This Boolean activation function mimics the exponential similarity function of Nosofsky’s (1986) GCM and Kruschke’s (1992) ALCOVE model when exemplar specificity is high, and simplifies our model by removing a free parameter. Exemplar activation propagates forward through the exemplar network to nodes representing category-level information. The activation of category node j, ω_j, is determined by the strength of the associative weight connecting exemplar node i with category node j, such that

$$ {\omega}_j=\sum \limits_i{\psi}_i{w}_{ij}. $$

(3)

Associations between category and exemplar nodes are updated on each trial in proportion to prediction error. We use the standard delta rule (Rescorla & Wagner, 1972), where changes in association weights are described by

$$ \varDelta {w}_{ij}=\lambda \left({t}_j-{\omega}_j\right), $$

(4)

where t is a teacher value determined by the feedback received on a given trial. Following Kruschke (1992), we use humble teachers, where

$$ {t}_j=\Big\{{\displaystyle \begin{array}{l}\max \left(+1,{\omega}_j\right),\mathrm{if}\ \mathrm{the}\ \mathrm{stimulus}\ \mathrm{is}\ \mathrm{in}\ \mathrm{Category}\ \mathrm{J}\\ {}\min \left(-1,{\omega}_j\right),\mathrm{if}\ \mathrm{the}\ \mathrm{stimulus}\ \mathrm{is}\ \mathrm{not}\ \mathrm{in}\ \mathrm{Category}\ \mathrm{J}\end{array}}. $$

(5)

Equation 4 states that the change in the association weight connecting exemplar node i with category node j is proportional to the difference between the teacher value and the activation value for category node j, which quantifies prediction error. Changes in associative weights on each trial are scaled by a learning rate parameter, λ.

In many category learning models, the learning rate parameter is held constant across trials. However, in probabilistic learning environments, where it is impossible to completely eliminate prediction error, several authors have argued that people might progressively discount feedback as prediction error becomes less informative (Craig et al., 2011; Kruschke & Johansen, 1999; see also Sewell et al., 2018). Following Kruschke and Johansen (1999), we consider a version of the learning model that incorporates feedback discounting by multiplying the learning rate on trial n by a discounting factor,

$$ r(n)=\frac{1}{1+\rho n}, $$

(6)

where ρ is a nonnegative discounting parameter. When ρ > 0, prediction errors encountered later in the task result in smaller changes in associative weights compared with equivalent errors encountered earlier in the task.

Equations 3–6 describe how changes in associative weights are driven by prediction error. To make contact with choice-RT data, relative associative strengths in the learning model must be related to drift rates that drive decision-making. Here, we assume a diffusion decision process that is identical to Ratcliff’s model. In our model, drift rates are determined by a nonlinear transformation of relative activation of the two category nodes.⁵ Given that changes in drift rates across learning blocks were consistent with an exponential function, we used a scaled softmax function to transform category activations to drift rates,

$$ v={v}_{\mathrm{r}}\left(\frac{\exp \left(\phi {\omega}_{\mathrm{A}}\right)}{\exp \left(\phi {\omega}_{\mathrm{A}}\right)+\exp \left(\phi {\omega}_{\mathrm{B}}\right)}-\tau \right). $$

(7)

Equation 7 is closely related to the response rule used by ALCOVE, where relative category node activation determines response probabilities via an exponentiated version of Luce’s (1959) choice rule, producing output bounded in the interval [0, 1]. The rate at which activation ratios approach either the upper or lower limit of the interval is determined by ϕ, with larger values resulting in more rapid approach. In ALCOVE, the role of the ϕ parameter is to set the level of determinism in responding. As ϕ increases, smaller differences in category activations result in a stronger tendency to assign the stimulus to the category with the higher level of activation.⁶ Although Eq. 7 does not control response outcomes directly, the functional significance of ϕ is similar, as it determines how relative category node activation maps onto relative evidence for different category outcomes during decision-making by setting drift rates. The drift threshold parameter, τ, ensures that relative category activations favoring each category outcome produce drift rates with the appropriate sign (i.e., v > 0 when ω_A > ω_B, and v < 0 when ω_A < ω_B). The value of τ determines the level of relative category node activation that results in a drift rate of zero (i.e., a drift rate that favors neither response alternative). In principle, τ can take on any value between zero and one. Logically, however, it is sensible to fix τ to an unbiased value of 0.5, so that v = 0 when ω_A=ω_B. Fixing τ in this way ensures symmetrical changes in drift rates as relative category activations deviate from a value of 0.5. The range of drift rates produced by Eq. 7 is controlled by the v_r parameter, which is positive-valued and freely estimated from the data. This parameter scales relative category activations within the interval [−τv_r, v_r (1 – τ)]; for example, when v_r = 1 and τ = 0.5, drift rates are scaled on the interval [−0.5, +0.5].

In total, the learning model has eight parameters that can be freely estimated from data. Two of these parameters govern the associative learning process. These are the learning rate parameter, λ, and the feedback discounting parameter, ρ. Four parameters govern the diffusion decision process: boundary separation, a, nondecision time, T_er, and trial-by-trial variability in drift rates, η, and nondecision time, s_t. The final two parameters link the learning and decision components of the model. These scaling constants, v_r and ϕ, set the range of learnable drift rates and control how differences in category node activations map onto drift rates, respectively.

Fits of the learning model to data

To fit the learning model to data, we generated 30 unique sequences of training stimuli (i.e., 30 different orderings of 200 learning trials). The structure of the training sequences mirrored those used experimentally. Training sequences were divided into five 40-trial blocks. Within each block, each stimulus was presented 10 times. The presentation order of stimuli within a block was determined randomly. For each training sequence, we evaluated model predictions after every 40 learning trials (i.e., at the end of each learning block). We then averaged the block-by-block predictions across the 30 training sequences, which were used as the basis for parameter estimation. Model predictions were generated in this way to ensure generalizability across different sequences of learning trials (Lewandowsky, 1995). As with the diffusion model analysis of the data, learning model parameters were estimated by minimizing G² (see Eq. 1).

We contrasted fits of two versions of the learning model to the data, which differed with regards to the inclusion of a feedback discounting mechanism (i.e., whether ρ in Eq. 6 was fixed to zero or freely estimated). The models therefore required either seven (no feedback discounting) or eight (feedback discounting) parameters to be freely estimated from the data.

The fit of the learning model (with no feedback discounting) is shown in Fig. 9. Best fitting parameters are shown in Table 2. In terms of quantitative fit, the learning model provides a close account of the data, G²(213) = 69.83, which nearly matches that of the version of the diffusion model that assumed exponential changes in drift rates across blocks (the exponential model; see Fig. 8). Like the exponential model, the learning model successfully predicts the relatively large change in choice probabilities for all four stimuli across the first two learning blocks. Critically, the model is able to account for the changes in accuracy while also characterizing the changes in the shapes of the RT distributions for correct and error responses. The learning model also correctly reproduces the pattern of error responses consistently being slower than correct responses throughout learning. Indeed, the quantitative predictions of the learning model are virtually indistinguishable from those of the exponential model. Particularly noteworthy is the fact that the non-drift-related parameter estimates are the same across the learning and exponential models.

Fig. 9

Fit of the integrated learning model (with no feedback discounting) to the data. Data are the same as in Figs. 6 and 8, and model predictions are presented in the same way as in Fig. 8. The learning model uses incremental changes in cue-category association weights to adaptively learn drift rates for individual stimuli across different trial blocks. Like the earlier diffusion model fits shown in Fig. 8, the learning model provides a close account of all major aspects of the data. Quantitatively, the fit is on par with that of the diffusion model

Table 2 Best fitting parameter estimates for the integrated learning model with no feedback discounting

We note here that while the fit of the integrated learning model is good, it is not perfect. Indeed, there are some aspects of the data that are not handled especially well by the model. For example, the shapes of the error RT distributions for the 0.2 and 0.8 stimuli in the first block of learning are not captured with the same precision as those for correct responses. In particular, the RT distributions appear to be less skewed in the tails compared with what is predicted by the model—the 0.7 RT quantile is consistently slower than predicted. However, it is worth noting that this aspect of the data was also missed by the version of the diffusion model that assumed exponential changes in drift rates across learning blocks. Given that the fit of the exponential model was about as good as could be expected from the diffusion model—recall that the fit of this model was not significantly worse than a model that allowed drift rates to vary freely across all learning blocks—it is perhaps unsurprising that the learning model would have similar difficulties with these aspects of the data. On balance, we believe that the theoretical benefits of a mechanistic interpretation of why drift rates change in an approximately exponential fashion—as predicted by error-driven learning—are substantial relative to these minor discrepancies between model predictions and data.

To further explore the learning dynamics in our task, we next considered a version of the learning model that progressively discounted feedback. Kruschke and Johansen (1999) argued for feedback discounting when learners are in probabilistic environments, as it is not possible to completely eliminate prediction error. Robust support for feedback discounting was found by Craig et al. (2011), and individual differences in feedback discounting—and how they relate to patterns of neural activity related to feedback processing—were recently investigated by Sewell et al. (2018). Whereas the feedback discounting parameter, ρ, was fixed to zero in the previous fits, we now freely estimated it from the data. As it turns out, this produced no improvement in fit, as the best fitting value of ρ was near zero, ΔG²(1) ≈ 0. We conclude that there was no evidence for feedback discounting in our study, and discuss potential reasons for this in the Discussion.

Application to individual data

Our analysis so far has focused on fits to group-averaged data, which combines the benefits of detailed observation at the individual level with the data-smoothing afforded by aggregation. To confirm that the general pattern of results were also present at the individual level, we fit the exponential model, the flexible model with free drift rates, and the learning model to each participant’s data. Model fits are summarized in Table 3. Perhaps unsurprisingly, the individual data were noisier than the group-averaged data, as can be gleaned from the higher values for G² for all models. However, for four participants (s2, s3, s4, and s5), the quality of fit provided by the integrated learning model was similar, if not better, than the fit of the exponential model. For the remaining participant, s1, the learning model performed noticeably worse than the other models. This was largely due to idiosyncrasies in the data for this participant that were not present to the same degree in other data sets (e.g., for some stimuli, there were erratic and nonmonotonic changes in choice probabilities across successive blocks). Because these anomalies in this participant’s data did not appear to be systematic, we did not explore more complex models. We note that s1 was one participant for whom the flexible model, with drift rates freely estimated across blocks, introduced a significant improvement in fit over the exponential model; the other being s5. We conclude that, on the whole, the patterns that we observed in the group-averaged data were also apparent at the individual level. Changes in drift rates tended to be well-described by an error-driven learning rule, and the quality of these fits closely resembled fits generated by assuming exponential changes in drift rates across blocks.

Table 3 G² fit values for the exponential model, flexible diffusion model, and integrated learning model at the level of individual participants

Summary of the learning model analysis

The diffusion model analysis of our learning data showed that variation in categorization performance was best accounted for in terms of changes in drift rate across learning blocks. These changes were well described by a simple exponential approach to a limit. The primary theoretical contribution of our study is showing that these changes in drift rates can be described mechanistically within an error-driven learning framework. The integrated learning model we developed produced fits to data that were virtually identical to those produced by the best performing version of the diffusion model (i.e., the exponential model). This is a novel insight, as the connection between associative learning processes and determinants of choice RT have only recently received detailed investigation (e.g., Frank et al., 2015; Pedersen et al., 2017; Ratcliff & Frank, 2012). Although our learning model incorporates a similar number of free parameters compared with the more descriptive exponential model, we believe that our model’s ability to explain why changes in drift rates are approximately exponential represents an important theoretical advance. It is striking that an essentially unmodified version of the Rescorla–Wagner learning rule is able to successfully account for the main patterns of change in choice-RT distribution data over the course of learning. Because the learning rule was developed to explain changes in choice behavior, there is no reason to expect it to also be able to account for RTs, especially at the level of entire families of RT distributions. That an error-driven learning process is so readily compatible with a decision process based on evidence accumulation speaks to the fundamental importance of these facets of cognitive processing.

Discussion

In this article, we investigated category learning performance in a simple probabilistic learning environment involving four highly discriminable cues, each with a unique feedback probability. We collected detailed RT distribution data spanning the entire course of learning by varying the perceptual properties of the cues across different runs of the experiment and aggregating responses across multiple testing sessions. Despite the large number of learning trials people completed—3,600 trials in total—people in our task responded by overshooting the feedback probabilities rather than strictly maximizing, which is consistent with existing data from single-session tasks (e.g., Craig et al., 2011). In terms of RTs, in addition to a practice effect, we found that the speed of responding was determined by both feedback probability as well as whether a response was correct or incorrect. Stimuli that were more strongly predictive of category outcomes—that is, when P(A) = 0.2 or 0.8—were responded to faster than stimuli that were weakly predictive of category outcomes—that is, when P(A) = 0.4 or 0.6. We also observed error responses that were consistently slower than correct responses (e.g., Ratcliff, Van Zandt, & McKoon, 1999). At the level of RT distributions, the RT difference for correct responses grew greater in the tails of the distributions, but was not affected by learning.

A diffusion model analysis of the learning data revealed that the changes in categorization performance could be accounted for solely by allowing drift rates to vary across learning blocks. We also considered versions of the model that allowed nondecision time and boundary separation to change during learning, but neither of these models improved fit to data. Changes in drift rates were well-described as an exponential approach to a limit, producing a fit to data that was comparable with a more flexible model that freely estimated two drift rates per learning block. The diffusion model analysis was consistent with the idea that learned changes in association weights was the main driver of performance in our task. A limitation of the diffusion model account, however, is that changes in associative strength could be inferred only indirectly via changes in drift rates. To investigate this claim in more detail, we developed an exemplar-based associative learning model based on ALCOVE (Kruschke, 1992), which used learned changes in associative weights to derive stimulus-specific drift rates across learning blocks. This integrated model of learning and decision-making provided an account of the data that was on par with that of the diffusion model, while providing a mechanistic account of how drift rates changed over the course of learning. The success of the integrated model is an important step in developing the link between error-driven models of associative learning on the one hand and evidence accumulation models of decision-making on the other hand. Before discussing future directions and broader extensions of the modeling framework, we first address some of the potential limitations of our study.

Potential limitations

One of the key methodological innovations of our study was using multiple testing sessions to obtain detailed RT distribution data from the earliest stages of learning. This entailed repeated presentation of the same logical task structure in separate experimental runs (i.e., people encountered a new set of stimuli every five blocks within each session). Because different stimuli were presented in different runs, contingencies relating cues to category outcomes had to be learned anew for each run. However, the practice effects in RT that we obtained in this task were rather muted compared with other categorization studies (cf. Nosofsky & Palmeri, 1997a; Palmeri, 1997). This is likely due to practice being a product of both stimulus-specific and task-general factors (Dutilh et al., 2011). In order to have enough trials to analyze performance at the level of RT distributions for correct and error responses, we had to aggregate data across both sessions and experimental runs. This means that, when considering changes in mean RT as a function of learning block (as in Fig. 5), the data would be dominated by responses made after people had acclimatized to various task factors (e.g., the physical appearance of stimuli, the timing of stimulus presentation during a trial, and the mapping of response keys to different category outcomes). This naturally removes the component of the practice effect that reflects improvements due to task-level familiarization effects. We believe, however, that the performance improvements we observed are an accurate reflection of benefits due to stimulus-specific factors (i.e., learning). This is because, regardless of how many sessions had been completed, people repeatedly needed to learn a new set of cue–outcome contingencies. Because our data captured stimulus-specific practice effects, it is an open question whether our integrated learning model would be able to account for larger practice effects that incorporate both stimulus-specific and task-specific factors via changes in drift rate alone. Typically, variation in nondecision time is needed to accommodate the large changes in RT that reflect task-level factors (e.g., Dutilh et al., 2011; Petrov et al., 2011). These changes appear to be separate from stimulus-specific learning processes, leading us to believe that our model-based characterization of the associative learning process is a general one.

Another potential limitation of our study was our use of a small number of stimuli in each experimental run. At any given point during the task, participants had to keep track of associations for only four nonconfusable stimuli. The unstructured nature of our categorization task differs from the majority of categorization research that has employed more structured stimulus sets. Typically, categorization-RT models address performance where stimuli are more numerous and potentially confusable with one another due to differences in similarity (e.g., Nosofsky & Palmeri, 1997a, 1997b). It is therefore unclear whether the modeling framework we have developed here can successfully scale up to more complex stimulus sets where the interitem similarity of stimuli is variable. This is an important target for future research that our lab is currently investigating. We note here that our choice of using a small set of nonconfusable stimuli was made to more effectively isolate the associative learning process for modeling purposes. Because people had to keep track of only four stimuli at a time, we hoped to avoid performance issues due to working memory capacity limitations (e.g., Cowan, 2001). By presenting people with discrete-valued nonconfusable stimuli, we were able to interpret changes in performance as reflecting incremental changes in cue–outcome associations. This simplified the task of modeling the data, as we sought to minimize the chance that people would use more complex strategies involving rule induction supplemented by exemplar memory for exceptions (e.g., Erickson & Kruschke, 1998; Nosofsky, Palmeri, & McKinley, 1994). Having established that an error-driven learning rule suffices to provide a complete account of performance with simple stimuli, it is likely that the modeling framework could be expanded to handle coordination of different kinds of category representations during learning as well (e.g., Sewell & Lewandowsky, 2011, 2012). We expand on this point when discussing rule-based models of categorization RT.

A third limitation is that we failed to find any evidence for a feedback discounting process, despite our use of a probabilistic learning task. This result stands in contrast to earlier work by Kruschke and Johansen (1999) and Craig et al. (2011), who both found that people tend to discount feedback as learning progresses (though see Sewell et al., 2018, for evidence of individual differences in feedback discounting). We suspect that our task may have been ill equipped to detect feedback discounting even if it were present. In our task, feedback probabilities were held constant throughout the learning period, which was relatively brief compared with other studies. For example, we evaluated learning across 200 trials in each experimental run. By contrast, Craig et al. had people complete 720 trials of learning, within a single experimental session. Intuitively, the effects of feedback discounting become more pronounced as the number of trials increases—as this allows for more time for the effect of feedback discounting to affect performance. It is also noteworthy that Craig et al. changed the training contingencies partway through their task to examine how quickly people would adjust to the shift. Under feedback discounting, people should be slower to adapt to the change. By keeping feedback probabilities constant in our task, we were not able to examine such adaptation effects. Moreover, because we made it clear when feedback contingencies were being reset (i.e., by changing the perceptual features of the stimuli across experimental runs and explicitly informing our participants), the need to regularly attend to feedback was constantly reiterated by the demands of the task. Continually refreshing the environment—with participants having full knowledge of when this occurred—likely minimized people’s tendency to discount feedback in our task.

One other potential limitation concerns the small sample size we used (N = 5). Although performance across individuals was overall quite consistent, there was some variability across individuals (e.g., s1 and s5 produced data that were better described by a diffusion model with freely varying drift rates rather than exponential changes in drift rate). This raises potential concerns about generalizability to broader populations. We are, of course, sympathetic to such concerns. However, we believe our small-N approach is appropriate, given our theoretical aims of exploring association-based frameworks for characterizing choice-RT data. As noted recently by Smith and Little (2018), study designs that permit extensive measurement at the individual level tend to be more informative for the purposes of theory development and testing. Although increases in sample size are always desirable for showcasing generalizability—provided they do not compromise measurement at the individual level—we believe the consistency of our results across individuals speaks to the generality of our main theoretical claims: A model that incorporates error-driven learning assumptions can produce fits that are of a comparable quality to a more flexible and less mechanistically defined diffusion model.

Other exemplar models of categorization RT

Our model is most closely related to the EBRW model of categorization RTs, and we view the two models as complementary to one another. The main point of distinction between our model and the EBRW model is that the framework we have developed provides a different, yet related, perspective on the learning process. Following the work of Kruschke (1992), our learning framework allows exemplars in memory to develop associations of varying strength with different category outcomes. This permits our modeling framework to be extended to address phenomena that appear to be beyond the current scope of the EBRW model. For example, by modeling learning in terms of trial-by-trial updating of associative strengths, our model could be used to investigate order-of-learning effects, such as blocking (Kamin, 1968; Sewell & Lewandowsky, 2012), which, to our knowledge, have not been addressed by the EBRW model. We do note, however, that order-of-learning effects have been successfully accounted for by related exemplar-based frameworks that view associative learning in terms of cued recall (e.g., MINERVA-AL; Jamieson, Crump, & Hannah, 2012). A potentially fruitful avenue for future research concerns the ability of various exemplar-based models to account for joint choice-RT data from studies designed to produce order-of-learning effects. Indeed, it remains an open question whether the RT distribution data from paradigms that produce order-of-learning effects can be accommodated by a traditional error-driven learning rule (or exemplar retrieval assumptions) or if additional assumptions are also required.

Our model is also related to the extended GCM (EGCM) developed by Lamberts (1998, 2000). The EGCM describes the time course of categorization in terms of within-trial dynamics. Rather than assuming that all features of a stimulus become available simultaneously, the EGCM posits that features are stochastically sampled as a function of perceptual salience. This allows the model to account for performance when people are under time pressure to respond, and can explain changes in interitem similarity as a function of processing time. Although our current focus on single-cue stimuli precludes a detailed discussion of the feature-sampling assumptions of the EGCM, we note that variation in the time course of stimulus encoding is captured by the nondecision time parameter, T_er, in our modeling framework. A goal for future research is to examine categorization RTs when stimuli comprise multiple cues—presented either as combinations of discrete elements (e.g., a red circle paired with a blue circle) or as integrated multidimensional stimuli. By manipulating encoding demands in this way, it would be possible to examine whether the time course of feature recruitment changes during learning. Lamberts (1995) showed that classification decisions are dominated by perceptually salient stimulus features when people are under extreme time pressure, but that diagnostic features determine responding when processing time is extended. It is likely that this relationship gradually emerges as people learn which features are most useful for discriminating between category alternatives. This leads to the expectation that time pressure will have different effects on performance during the early and late stages of learning. Specifically, that performance under time pressure will tend to be guided by the most salient stimulus feature regardless of learning, whereas a shift from reliance on salient to diagnostic features would be expected as learning progresses. Incorporating the EGCM’s feature sampling assumptions to model such changes in performance would require the drift rate in our decision model to change dynamically over the course of a single trial (e.g., Holmes, Trueblood, & Heathcote, 2016). Extending the model in this way is a complex, but fascinating prospect for future research.

Rule-based models of categorization RTs

Although we have adopted an exemplar-based perspective on category representation here, there has recently been renewed interest in developing rule-based models of categorization RT. Some of the most detailed recent developments have been made within the logical rules framework of Fifić, Little, and Nosofsky (2010). This framework extends decision-bound representations of categorization RT (e.g., Ashby, Boynton, & Lee, 1994; Ashby & Maddox, 1994) by assuming that categorization decisions are based on the combination of separate decisions about feature values along different stimulus dimensions. The framework is designed to address data at the level of RT distributions and can identify differences in the processing architectures people use when classifying different kinds of perceptual stimuli (e.g., if rules for different stimulus dimensions are evaluated serially or in parallel and whether decisions proceed independently or interact with one another). For example, classification of perceptually separable stimuli produces a RT profile that is consistent with independent processing of stimulus features (Fifić et al., 2010; Little, Nosofsky, & Denton, 2011; Moneer, Wang, & Little, 2016). By contrast, perceptually integral stimuli are processed more holistically via coactive processing of different features (Little, Nosofsky, Donkin, & Denton, 2013).

The logical rules models developed by Nosofsky and colleagues have accounted for asymptotic responding in highly practiced observers. An open question is whether the models could also be expanded to account for learning effects. Little, Wang, and Nosofsky (2016) recently explored extensions to the logical rules models as well as the EBRW model to address sequence effects in the Garner (1974) speeded classification paradigm. One potential way to expand the rule-based models to address trial-by-trial learning would be to allow the response regions formed by different rules to develop associations with different category outcomes through error-driven learning (cf. Erickson & Kruschke, 1998). Alternative ways include sampling algorithms that have been used in Bayesian hypothesis testing models, where the likelihood of applying a specific rule changes adaptively as people receive feedback from the learning environment (e.g., Goodman, Tenenbaum, Feldman, & Griffiths, 2008; Sanborn, Griffiths, & Navarro, 2010). Incorporating ways for rule-based models to address trial-by-trial learning would open the door to investigating ways in which rule-based and exemplar-based representations might interact during learning (e.g., Erickson & Kruschke, 1998; Nosofsky et al., 1994). Previous research has relied on patterns of accuracy data to identify the relative contributions of rule-based and exemplar-based representations to performance, but introduction of RT data would impose stronger constraints. For example, in rule-plus-exception category structures (e.g., Denton, Kruschke, & Erickson, 2008; Erickson & Kruschke, 1998, 2002), responses to different stimuli can be viewed as a probability mixture of (1) trials where a categorization rule was applied and (2) trials where decisions were based on exemplar similarity. Addressing such data with a quantitative framework incorporating elements of both rule-based and exemplar-based models of RT would reveal how learning affects factors such as retrieval latencies for rules and exemplars, as well as how decision-relevant information from different kinds of representations is modified in light of task experience. For example, do drift rates for rule-based and exemplar-based responses change at different rates during learning? The model we have developed here provides a proof of concept that exemplar-based associative learning models can explain categorization RTs. A similar framework can then be applied to develop analogous rule-based learning models, which would open the door to developing more complete rule-plus-exemplar models of category learning.

Diffusion and accumulator models of decision-making

In this article, we have assumed a decision model based on the diffusion process. In diffusion decision models, accumulated evidence is represented as a single signed total, where evidence for one response alternative is simultaneously evidence against the other. Accumulator models offer an alternative to this view. Rather than representing a single signed evidence total, there are multiple evidence totals, one for each response alternative, represented in separate accumulators. Different models make different assumptions about whether accumulators inhibit one another (Brown & Heathcote, 2005; Usher & McClelland, 2001), or operate independently (Brown & Heathcote, 2008; Smith & Vickers, 1988). We have not investigated accumulator representations of the decision process, but consider how the choice of decision model might affect our theoretical framework. The most straightforward way of combining a learning network with an accumulator-based decision mechanism would be to assume that the drift rates for the two different response alternatives are equal to the respective category node activations, v_A = ω_A and v_B = ω_B. This contrasts with our model, where we assumed that the information driving the decision process was based on a normalized representation of relative associative strength (see Eq. 7). We did consider simpler alternatives to Eq. 7, where drift rates were computed on the basis of the difference in category node activations. These difference models are conceptually related to the idea that drift rates for different accumulators are set by category node activation values. We did not present these alternatives in this article, and ultimately rejected them because they could not produce appropriate learning dynamics for our task. We conjecture that computation of drift rates for an accumulator-based decision mechanism would also have to include a normalizing factor, and would potentially mirror Eq. 7. Regardless of whether the decision process is modeled as a diffusion or accumulator-based process, we believe it is likely that the way learning performance would be described—in terms of which model parameters are affected by the associative learning process—would be similar (Donkin, Brown, Heathcote, & Wagenmakers, 2011). Both classes of models incorporate parameters that serve similar functions and have common psychological interpretations. For example, drift rates in both diffusion and accumulator models map onto the quality of evidence driving the decision process, setting the rate at which decision-relevant information is accumulated. The conceptual overlap between the different classes of decision models leads us to believe that learning would be captured by analogous model parameters regardless of the class of decision model used. We leave development and testing of an accumulator-based decision model to future theoretical work.

Future directions

In addition to the broad theoretical extensions mentioned above, there are several other ways in which the current work could be extended. In this article, we focused on learning performance when categorization accuracy was emphasized. Although people were encouraged to respond within 2,000 ms of stimulus presentation, time pressure did not appear to impose any major limitations on performance (e.g., the slowest RTs were around 1,000 ms; see Fig. 6). An open question is how performance in our task would be affected by imposing time pressure during learning. Traditionally, differences in performance across speed and accuracy emphasis have been modeled via changes in the decision threshold people use (e.g., boundary separation in the diffusion model). However, recent work has shown that this account of the speed–accuracy trade-off is not always accurate, and that sometimes speed emphasis produces changes in both the decision threshold and information people use to make decisions (Rae, Heathcote, Donkin, Averell, & Brown, 2014). If it is possible for people to change the information they use to make a decision when speed is emphasized, then it is also possible that the amount of information people extract from task feedback is affected. Currently, it is not known how learning is affected by processes related to setting decision thresholds, but there are at least two possibilities. One is that a decision threshold is closely linked to the amount of information people can extract from feedback on a given trial. Because a decision threshold reflects an individual’s preference for how much evidence they require before making a choice, the informativeness of feedback may vary if deviations from one’s preferred decision threshold are required by the task (e.g., under speed emphasis). When boundary separation is large, and people make decisions more cautiously, error feedback is especially informative, as it signals a discrepancy between the expected and observed outcome, despite requiring a large quantity of evidence to accrue before making the response. By contrast, when speed is emphasized and a lower decision threshold is used, error feedback would be less informative because of the lower standard of evidence required before making a choice. An alternative is that the learning and decision-making processes operate independently of one another, and the threshold applied when making a categorization decision is unrelated to the rate at which learning proceeds. We can test between these alternatives using our model by examining whether speed emphasis produces a change in the associative learning rate parameter, λ, in addition to a reduction in boundary separation.

Another avenue for future research is to examine how people perform when presented with multiattribute stimuli presented as combinations of discrete cues. Consider a task where people are trained on a set of cue-category associations similar to what participants in our task learned. Subsequently, pairwise combinations of cues could be presented in a transfer phase (e.g., a red circle paired with a blue circle). Such a design would provide a strong test of how associative information for different cues are combined and used to compute drift rates. Varying the composition of the cue compounds can also be used to assay the time course of retrieval of associative information from memory. For example, contrasting the onset of responses for stimuli comprising a single cue versus multiple copies of the same cue (e.g., a red circle vs. a red circle paired with another red circle) can establish whether redundancy in the stimulus results in a reduction in nondecision time, reflecting faster retrieval time, an increase in the drift rate for the redundant compound compared with the single-cue stimulus, or both. Both instance theory and the EBRW model would predict faster retrieval times for a redundant compound, as each component of the compound would trigger an independent attempt to retrieve the relevant associative information from memory. Increases in drift rate for a redundant stimulus compound would imply that multiple presentations of a cue results in multiple activations of the relevant cue–outcome associations, resulting in more discriminative category information being available for decision-making. For fixed values of ω_A and ω_B, doubling the category activation values would result in no change in the ratio of category node activations, but by Eq. 7 would produce more extreme-valued drift rates. The range of effects that various combinations of cues could have on both choice probabilities and RTs would provide in a strong test of the learning model we have developed here.

A third way of extending the current work would be to consider the effects of selective attention on performance. By presenting people with multidimensional stimuli comprising features that are of varying predictive utility, we could incorporate an attention learning mechanism akin to the one used in ALCOVE (Kruschke, 1992). This would better link the learning model we have developed here with both the GCM and ALCOVE, which make extensive use of selective attention mechanisms. Supplementing our learning model in this way would also provide a strong test of the idea that selective attention is learned via prediction error, as the model would have to be evaluated not just against categorization outcomes, but also RTs. The dynamics of how an attention learning mechanism affects categorization RTs has not been previously examined in the literature, and so its compatibility with RT data is an open question. Because learned selective attention increases the influence of categorically diagnostic sources of information while minimizing the influence of nondiagnostic information, it accelerates learning, producing more rapid changes in cue–outcome associations that promote accurate responding. In the context of our model, this would result in faster changes in drift rates, which may or may not be consistent with how the shapes of RT distributions change during learning. Testing an extension of the model against RT data in this way may also be useful in distinguishing reliance on rules versus exemplar similarity, as selective attention can make exemplar models mimic choice probability predictions of rule-based models.

Conclusions

In this article, we examined associative learning performance in a simple probabilistic categorization task. The specific aim of our study was to investigate changes in the shapes of RT distribution data as people learn cue–outcome contingencies that varied in strength. We found that, people’s responses were consistent with overshooting, and that this pattern of responding persisted despite people completing many repetitions of the task across multiple testing sessions. We also found that, similar to other perceptual decision-making tasks, correct responses tended to be faster than error responses, and that the speed advantage was fairly consistent across learning blocks.

We conducted a diffusion model analysis of the learning data and found that changes in performance could be explained solely in terms of changes in drift rates. There was no support for changes in either encoding efficiency, as indexed by nondecision time, or decision threshold as learning progressed. The changes in drift rates we observed were well characterized by an exponential approach to a limit. We then developed a process account of the changes in drift rates by combining an error-driven associative learning model with a diffusion decision model. This integrated model attributed changes in categorization performance to trial-by-trial changes in the strength of associations linking representations of cues to different category outcomes. The integrated learning model successfully accounted for both the changes in choice probabilities and the shapes of RT distributions for different category responses at the individual stimulus level. Our new model strengthens the ties between existing exemplar-based models of the time course of decision-making (e.g., Logan, 1988, 2002; Nosofsky & Palmeri, 1997a, 2015) and learning (e.g., Kruschke, 1992) by showing that an error-driven learning rule suffices to jointly account for both facets of performance.