Abstract
Long-term radio monitoring of the broad absorption line (BAL) quasar Mrk 231 at 17.6 GHz detected a strong flare in 2015. This triggered four epochs of Very Long Baseline Array (VLBA) observations from 8.4 to 43 GHz as well as three epochs of X-ray observations with NuSTAR and two with XMM over a 15 week period. Two ejected components were detected by the VLBA observations. A conservative lower bound on the apparent speed of the first ejection is attained by assuming that it was ejected when the flare began, 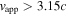 . Serendipitous far-UV Hubble Space Telescope observations combined with our long-term radio monitoring seem to indicate that episodes of relativistic ejections suppress flux that is emitted at wavelengths shortward of the peak of the far-UV spectral energy distribution, similar to what has been observed in radio-loud quasars. Episodes of strong jet production also seem to suppress the high-ionization BAL wind seen in weak jet states. We found a statistically significant increase (
. Serendipitous far-UV Hubble Space Telescope observations combined with our long-term radio monitoring seem to indicate that episodes of relativistic ejections suppress flux that is emitted at wavelengths shortward of the peak of the far-UV spectral energy distribution, similar to what has been observed in radio-loud quasars. Episodes of strong jet production also seem to suppress the high-ionization BAL wind seen in weak jet states. We found a statistically significant increase ( ) of the 3–12 keV flux during the radio flare relative to a quiescent radio state. This is explained by an ultra-fast (∼0.06c) X-ray-absorbing photoionized wind that is significantly detected only in the low-radio state (similar to Galactic black holes). Mrk 231 is becoming more radio loud. We found that the putative parsec-scale radio lobe doubled in brightness in nine years. Furthermore, large flares are more frequent, with three major flares occurring at ∼2 year intervals.
) of the 3–12 keV flux during the radio flare relative to a quiescent radio state. This is explained by an ultra-fast (∼0.06c) X-ray-absorbing photoionized wind that is significantly detected only in the low-radio state (similar to Galactic black holes). Mrk 231 is becoming more radio loud. We found that the putative parsec-scale radio lobe doubled in brightness in nine years. Furthermore, large flares are more frequent, with three major flares occurring at ∼2 year intervals.
Export citation and abstract BibTeX RIS
1. Introduction
Mrk 231, at a redshift of z = 0.042, is a nearby radio-quiet quasar (RQQ) with a relativistic jet (Reynolds et al. 2009). The jet is extremely powerful for an RQQ during flare states, with a kinetic luminosity estimated to be  erg
erg  for previous flares. Consequently, we have been monitoring the radio behavior at ∼20 GHz for the last seven years. Since 2011, we have detected three large blazar-like flares (see Reynolds et al. 2013b) with flux densities
for previous flares. Consequently, we have been monitoring the radio behavior at ∼20 GHz for the last seven years. Since 2011, we have detected three large blazar-like flares (see Reynolds et al. 2013b) with flux densities  mJy at ∼20 GHz. The last of these major flares initiated a target of opportunity (ToO) four-epoch Very Long Baseline Array (VLBA) observation. We were also afforded director's discretionary time for three observations with the NuSTAR X-ray telescope and two observations with the XMM X-ray telescope.
mJy at ∼20 GHz. The last of these major flares initiated a target of opportunity (ToO) four-epoch Very Long Baseline Array (VLBA) observation. We were also afforded director's discretionary time for three observations with the NuSTAR X-ray telescope and two observations with the XMM X-ray telescope.
Mrk 231 is a unique laboratory for studying the multiple aspects associated with the quasar phenomenon. It is one of a small number of RQQs that have clearly exhibited episodes of relativistic jet formation (Brunthaler et al. 2000; Blundell et al. 2003). It also supports broad absorption line (BAL) winds. We use the original definition of BAL quasars (BALQSOs) as quasars with UV-absorbing gas that is blueshifted at least 5000 km s−1 relative to the QSO rest frame and displaying a spread in velocity of at least 2000 km s−1, (Weymann et al. 1991). This definition excludes the so-called "mini-BALQSOs," with the BALnicity index = 0 (Weymann 1997), and this definition is preferred here since mini-BALQSOs tend to resemble non-BALQSOs more than BALQSOs in many spectral and broadband properties (Punsly 2006; Zhang et al. 2010; Bruni et al. 2013; Hayashi et al. 2013). A nonzero BALnicity index is extraordinary considering that the existence of large-scale jets and BAL winds are almost mutually exclusive. The propensity for suppressed large-scale emission increases strongly with BALnicity index (Becker et al. 2000, 2001). Thus, episodes of relativistic jet production in Mrk 231 allow us to explore the interplay between BAL winds and jets. Mrk 231 is exceptional in that it tends to vacillate between radio-quiet and radio-loud behaviors. In particular, in this study we find that states of weak jet activity have UV characteristics that differ from those of states of high jet activity. Based on limited data, the weak jet state shows evidence of high-ionization BAL winds, which, as noted above, is a property associated with RQQs. In states of high jet activity, the evidence of a high-ionization BAL wind disappears and the spectral energy distribution (SED) steepens beyond its peak in the far-UV, a property common to radio-loud quasars (Telfer et al. 2002; Punsly 2015). This transition between high jet activity and low jet activity occurs on very short timescales in some Galactic black holes (Klein-Wolt et al. 2002; Prat et al. 2010). Consequently, these stellar mass objects form the basis of our physical understanding of the state change (both back and forth) between a jetted black hole accretion system to a non-jetted black hole accretion system. It is not clear that the trends observed in Galactic black holes extrapolate many orders of magnitude in both time and space to quasars. This was the motivation for our previous high-frequency (15, 22 and 43 GHz) VLBA observations (Reynolds et al. 2009). Our previous VLBA observation detected a strong 22 GHz flare that emerged from the core between epochs 2006.07 and 2006.32 ( increase in less than three months). However, we learned that the putative ejecta faded very rapidly and required both high resolution (43 GHz) and high sensitivity. Thus, we recognized the need to observe a strong flare that was still growing and to improve the sensitivity by choosing a higher data sampling rate, 2 Gbps (as opposed to the 256 Mbps that was previously available). This observation challenged the limits of the VLBA and our efforts were designed to maximize the likelihood of successful phase-referencing and subsequent self-calibration of the weak target source. In order to determine the initiation of a ToO for our VLBA observations, we began monitoring Mrk 231 at 22 GHz in 2009, switching to 17.6 GHz in 2012. The details of our monitoring program and the discovery of a large flare were previously reported (Reynolds et al. 2013b).
increase in less than three months). However, we learned that the putative ejecta faded very rapidly and required both high resolution (43 GHz) and high sensitivity. Thus, we recognized the need to observe a strong flare that was still growing and to improve the sensitivity by choosing a higher data sampling rate, 2 Gbps (as opposed to the 256 Mbps that was previously available). This observation challenged the limits of the VLBA and our efforts were designed to maximize the likelihood of successful phase-referencing and subsequent self-calibration of the weak target source. In order to determine the initiation of a ToO for our VLBA observations, we began monitoring Mrk 231 at 22 GHz in 2009, switching to 17.6 GHz in 2012. The details of our monitoring program and the discovery of a large flare were previously reported (Reynolds et al. 2013b).
The paper is organized as follows. Section 2 describes the observational details of our monitoring. In Section 3, we describe the VLBA observations that were triggered on 2015 March 31. There were four observations, at 8.4, 15.2, 22.2, and 43 GHz, that were spread out over 15 weeks. In Section 4, we describe Hubble Space Telescope (HST) observations of the far-UV spectrum of Mrk 231 that serendipitously align with three epochs of our radio monitoring. In Section 5, we discuss the X-ray telescope observations that were granted after our VLBA ToO, three NuSTAR observations, and two XMM observations. Throughout this paper, we adopt the following cosmological parameters: H0 = 71 km s−1 Mpc−1,  and
and  .
.
2. The Radio Monitoring
Reynolds et al. (2013b) reported the methods of our radio monitoring program. In summary, the program utilized long-term monitoring with the VLA (Very Large Array) and EVLA (Expanded Very Large Array) at 22 GHz from 2009 to 2012 and from 2013 to 2015 Arcminute Microkelvin Imager (AMI; Zwart et al. 2008) at 13.5–18 GHz.8 The long-term monitoring data from Reynolds et al. (2013b) are plotted in the top frame of Figure 1. This light curve incorporates historical data both from the literature (McCutcheon & Gregory 1978; Edelson 1987; Ulvestad et al. 1999a, 1999b; Reynolds et al. 2009) and from the VLA public archive (project codes AB783, AN030, AU015). We have superimposed the times of relevant observations that we will reference in the following. The notable features of the historical light curve are the major flare of 2013 that was monitored with AMI and analyzed previously (Reynolds et al. 2013b). It was shown that this is similar to blazar flares (rise time, decay, and relative magnitude), but on a smaller scale. The unexpected steady rise of flux failed to meet our trigger criteria (which were then revised) and we missed this opportunity to study a flare in progress. The other important feature is the HST Faint Object Spectrograph (FOS) observation with the G160L grating on 1996 November 21, just 14 days before the historically low VLA flux density measurement (Ulvestad et al. 1999a). This fortuitous circumstance will form an important part of our analysis in Section 4. Another fortuitous circumstance is the HST Cosmic Origins Spectrograph (COS) observation with the G130M grating on 2011 October 15 reported in Veilleux et al. (2013) that occurred during a 22 GHz flare.
Figure 1. Top frame is the historic ∼20 GHz light curve from Reynolds et al. (2013b) with the timing of observations in other energy bands that are discussed in this paper superimposed. The bottom frame is an AMI 17.6 GHz light curve showing the initiation of the radio flare discussed in this article.
Download figure:
Standard image High-resolution imageThe bottom frame of Figure 1 is the 17.6 GHz (the highest usable frequency) light curve from our more recent AMI monitoring. The 2013 flare is on the left-hand side. The outlier data points with large error bars during the flare decay are affected by poor weather (precipitation). We were unable to correct for the weather, and they should not be considered as evidence of rapid flux changes. The 2015 flare appears on the right-hand side of the figure. The VLBA observations (and subsequent coordinated X-ray observations) were triggered on 2015 March 31. The flare was still rising and approaching the peak flux density, so the timing was ideal for our program—the maximum brightness for study during the flare rise. Knowing that the detected fluxes were going to be small at the crucial frequency of 43 GHz, achieving maximum brightness was essential to the success of the observation. The other interesting feature of the light curve is timing of the HST COS observation with the G140L grating on 2014 December 13. The flare was already beginning at this time at 17.6 GHz, and as discussed in the next two sections, due to synchrotron self absorption (SSA) optical depth effects, the 43 GHz flare began at least a few days to weeks earlier. Again, this is fortuitous timing of the HST observation. All three of the far-UV HST observations serendipitously occurred during times of radio monitoring.
3. VLBA Observations
The VLBA project, BR205, successfully acquired data from all 10 stations during each of the four epochs of observation. The data were correlated on the VLBA correlator (Deller et al. 2011) and calibrated with NRAO's Astronomical Imaging Processing System using the ParselTongue interface (Kettenis et al. 2006).
Our observations were phase-referenced to J1302+5748 ( from Mrk 231) at 8.4, 15, 22, and 43 GHz, following the strategies described in Reynolds et al. (2009) for project BP124. J1311+5513 (≳80 mJy of unresolved flux density at 43 GHz) was used as a secondary calibrator to check the quality of the phase-referencing. For each epoch of our VLBA monitoring, two 4 hr observations with almost continuous recording at 2 Gbps (256 MHz bandwidth, dual polarizations) were acquired in order to achieve the signal-to-noise ratio required to resolve the putative subcomponents of the 43 GHz core and to maximize the likelihood of successful phase-referencing and subsequent self-calibration of the weak target source, Mrk 231. For scheduling purposes, the 4 hr blocks were split into two consecutive days, except for the last epoch in which both blocks occurred in a continuous time interval. After calibration overhead, this resulted in 2.6 hr on Mrk 231 per epoch, which was split into 0.25, 0.35, 0.8, and 1.2 hr at frequencies of 8, 15, 22, and 43 GHz, respectively. All four Stokes parameters were correlated and we were able to achieve naturally weighted image rms values in Stokes I of approximately 50, 100, 50, and 70 μJy at 8.4, 15, 22, and 43 GHz, respectively.
from Mrk 231) at 8.4, 15, 22, and 43 GHz, following the strategies described in Reynolds et al. (2009) for project BP124. J1311+5513 (≳80 mJy of unresolved flux density at 43 GHz) was used as a secondary calibrator to check the quality of the phase-referencing. For each epoch of our VLBA monitoring, two 4 hr observations with almost continuous recording at 2 Gbps (256 MHz bandwidth, dual polarizations) were acquired in order to achieve the signal-to-noise ratio required to resolve the putative subcomponents of the 43 GHz core and to maximize the likelihood of successful phase-referencing and subsequent self-calibration of the weak target source, Mrk 231. For scheduling purposes, the 4 hr blocks were split into two consecutive days, except for the last epoch in which both blocks occurred in a continuous time interval. After calibration overhead, this resulted in 2.6 hr on Mrk 231 per epoch, which was split into 0.25, 0.35, 0.8, and 1.2 hr at frequencies of 8, 15, 22, and 43 GHz, respectively. All four Stokes parameters were correlated and we were able to achieve naturally weighted image rms values in Stokes I of approximately 50, 100, 50, and 70 μJy at 8.4, 15, 22, and 43 GHz, respectively.
The observations were generally successful except for one major unexpected technical issue. Due to scheduling constraints, we could not be granted a continuous 8 hr observation. The compromise of splitting the observation into 4 hr increments on consecutive days proved deleterious in epochs 2 and 3 as the two segments were observed at almost the same Local Sidereal Time (LST). The resulting beam was poorly shaped due to insufficient u−v coverage and the resolution was inadequate for resolving structures along the jet. We analyze the resulting data even though this circumstance made it impossible to directly monitor motion along the jet (a primary objective of the program).
Figure 2 is the 17.6 GHz light curve of the 2015 flare. The flare initiates at the beginning to middle of 2014 December. The relevant VLBA, HST, XMM and NuSTAR observations times are indicated relative to the light curve. Table 1 lists the results of our model fits to the VLBA observation. There are four components listed in column (1), the core, K1: a stationary secondary 0.8 pc from the core that has been detected in previous VLBA observations, and two new components, K2 and K3. We discuss whether K2 and K3 might be the same component in this section. New components are only detected in epochs 1 and 4, presumably due to an inopportune beam shape in epochs 2 and 3. Column (2) is the date of the observation. The flux density of the component is listed in column (3). The uncertainty in the flux density is listed in the column (4). The next four columns are the X (east–west) and Y (north–south) coordinates (relative to the phase center) of each fitted component and the associated uncertainty. Notice that the origin (phase center) is close to K1, not to the core, due to the fact that the early position determination was done at low frequency where the steep spectrum K1 component dominates (Reynolds et al. 2009). Columns (9)–(11) describe the fitted elliptical Gaussian or point source models for each component. We list the major axis, the axial ratio, and the position angle. The last column is the frequency of observation.
Figure 2. AMI 17.6 GHz light curve of the 2015 flare. Note the dates of the observations discussed in this article.
Download figure:
Standard image High-resolution imageTable 1. Summary of Model Fits to VLBA Observations
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Component | Epoch | Flux | Flux | X | X | Y | Y | Major | Axial | PA | Frequency |
| Density | Density σ | σ | σ | Axis | Ratio | ||||||
| (Jy) | (Jy) | (mas) | (mas) | (mas) | (mas) | (mas) | (deg) | (GHz)) | |||
| Epoch | 1 | ||||||||||
| K1 | 2015.247 | 0.215 | 0.011 | 0.171 | 0.001 | 0.101 | 0.001 | 0.33 | 0.83 | −80.1 | 8.42 |
| Core | 2015.247 | 0.071 | 0.004 | 1.205 | 0.002 | 0.582 | 0.003 | 0.17 | 0.93 | 48.4 | 8.42 |
| K1 | 2015.247 | 0.093 | 0.005 | 0.186 | 0.001 | 0.103 | 0.002 | 0.29 | 0.77 | −85.5 | 15.3 |
| Core | 2015.247 | 0.094 | 0.005 | 1.259 | 0.001 | 0.601 | 0.002 | 0.12 | 0.00 | 85.8 | 15.3 |
| K1 | 2015.247 | 0.052 | 0.004 | 0.148 | 0.002 | 0.149 | 0.003 | 0.28 | 0.72 | −85.3 | 22.2 |
| Core | 2015.247 | 0.083 | 0.006 | 1.236 | 0.001 | 0.657 | 0.002 | 0.11 | 0.63 | 88.2 | 22.2 |
| Core | 2015.247 | 0.045 | 0.005 | 1.253 | 0.001 | 0.613 | 0.001 | 0.10 | 0.00 | 49.6 | 43.1 |
| K1 | 2015.247 | 0.018 | 0.002 | 0.137 | 0.002 | 0.097 | 0.004 | 0.29 | 0.52 | 73.5 | 43.1 |
| K2 | 2015.247 | 0.002 | 0.001 | 0.939 | 0.017 | 0.449 | 0.030 | 0.00 | 1.00 | 0.00 | 43.1 |
| Epoch | 2 | ||||||||||
| K1 | 2015.296 | 0.228 | 0.011 | 0.285 | 0.001 | 0.095 | 0.001 | 0.45 | 0.62 | 68.3 | 8.42 |
| Core | 2015.296 | 0.069 | 0.003 | 1.344 | 0.004 | 0.587 | 0.004 | 0.18 | 0.00 | −58.2 | 8.42 |
| K1 | 2015.296 | 0.098 | 0.005 | 0.186 | 0.002 | −0.023 | 0.002 | 0.26 | 0.88 | −83.2 | 15.3 |
| Core | 2015.296 | 0.094 | 0.005 | 1.250 | 0.005 | 0.471 | 0.002 | 0.07 | 0.61 | −14.9 | 15.3 |
| K1 | 2015.296 | 0.057 | 0.004 | 0.225 | 0.002 | 0.080 | 0.002 | 0.27 | 0.95 | 52.9 | 22.2 |
| Core | 2015.296 | 0.083 | 0.006 | 1.295 | 0.001 | 0.580 | 0.002 | 0.17 | 0.45 | 24.2 | 22.2 |
| Core | 2015.296 | 0.044 | 0.004 | 1.315 | 0.002 | 0.580 | 0.002 | 0.14 | 0.00 | 67.5 | 43.1 |
| K1 | 2015.296 | 0.018 | 0.002 | 0.214 | 0.005 | 0.073 | 0.004 | 0.25 | 0.57 | 88.1 | 43.1 |
| Epoch | 3 | ||||||||||
| K1 | 2015.452 | 0.259 | 0.013 | 0.186 | 0.001 | 0.007 | 0.001 | 0.43 | 0.62 | 68.4 | 8.42 |
| Core | 2015.452 | 0.070 | 0.004 | 1.237 | 0.015 | 0.485 | 0.005 | 0.33 | 0.00 | 19.9 | 8.42 |
| K1 | 2015.452 | 0.104 | 0.005 | 0.137 | 0.003 | −0.052 | 0.002 | 0.33 | 0.57 | 26.9 | 15.3 |
| Core | 2015.452 | 0.077 | 0.004 | 1.183 | 0.004 | 0.422 | 0.003 | 0.31 | 0.00 | 45.4 | 15.3 |
| K1 | 2015.452 | 0.057 | 0.004 | 0.110 | 0.002 | −0.083 | 0.002 | 0.24 | 0.87 | 86.4 | 22.2 |
| Core | 2015.452 | 0.055 | 0.004 | 1.175 | 0.002 | 0.401 | 0.002 | 0.14 | 0.32 | 21.3 | 22.2 |
| Core | 2015.452 | 0.027 | 0.003 | 1.233 | 0.003 | 0.408 | 0.003 | 0.08 | 0.38 | 78.7 | 43.1 |
| K1 | 2015.452 | 0.020 | 0.002 | 0.150 | 0.004 | −0.092 | 0.004 | 0.24 | 0.87 | 86.4 | 43.1 |
| Epoch | 4 | ||||||||||
| K1 | 2015.529 | 0.262 | 0.013 | 0.155 | 0.002 | 0.006 | 0.004 | 0.29 | 0.71 | −64.3 | 8.42 |
| Core | 2015.529 | 0.063 | 0.003 | 1.181 | 0.010 | 0.482 | 0.015 | 0.21 | 0.00 | −8.2 | 8.42 |
| K1 | 2015.529 | 0.096 | 0.005 | 0.085 | 0.002 | −0.058 | 0.003 | 0.28 | 0.44 | −88.1 | 15.3 |
| Core | 2015.529 | 0.048 | 0.002 | 1.146 | 0.004 | 0.426 | 0.007 | 0.18 | 0.00 | 63.0 | 15.3 |
| K1 | 2015.520 | 0.066 | 0.005 | 0.066 | 0.001 | −0.071 | 0.002 | 0.24 | 0.54 | −80.3 | 22.2 |
| Core | 2015.529 | 0.042 | 0.003 | 1.142 | 0.002 | 0.423 | 0.003 | 0.08 | 0.00 | 64.1 | 22.2 |
| Core | 2015.529 | 0.032 | 0.003 | 1.205 | 0.002 | 0.422 | 0.004 | 0.21 | 0.00 | 67.0 | 43.1 |
| K1 | 2015.529 | 0.025 | 0.002 | 0.071 | 0.003 | −0.097 | 0.005 | 0.22 | 0.69 | −69.5 | 43.1 |
| K3 | 2015.529 | 0.003 | 0.001 | 1.049 | 0.027 | 0.247 | 0.042 | 0.00 | 1.00 | 0.00 | 43.1 |
Download table as: ASCIITypeset image
In Figure 3, we show the radio images for 8.4, 15.3 and 22.2 GHz. These images are relatively low resolution for this study and do not indicate any interesting nuclear morphology. The resultant flux densities of the core are important for determining the core spectrum in each epoch. These images are similar to the low resolution images in Reynolds et al. (2009). At 8.4 GHz, component K1 is dominant and the source is only partially resolved. At 15.3 GHz, the two components are resolved with roughly equal flux densities. Finally, at 22.2 GHz, the core is brighter except during the flare decay. The differences in apparent morphology at a given frequency are primarily a result of beam shape. Notice the elongated beam shape along the direction from the core to K1 in epochs 2 and 3. This greatly degraded the resolution along the jet direction in the critical 43.1 GHz observations during these epochs.
Download figure:
Standard image High-resolution imageDownload figure:
Standard image High-resolution imageDownload figure:
Standard image High-resolution imageFigure 3. (a) VLBA images at 8.4 (top left), 15.3 (top right), and 22.2 GHz (bottom) from epoch 1. In each case the bottom contour is 0.1 mJy/beam increasing in factors of 2. The data have been weighted with Briggs' weighting scheme (Briggs 1995) using a robustness parameter of 0. (b) VLBA images at 8.4 (top left), 15.3 (top right), and 22.2 GHz (bottom) from epoch 2. In each case the bottom contour is 0.1 mJy/beam increasing in factors of 2. The data have been weighted with Briggs' weighting scheme (Briggs 1995) using a robustness parameter of 0. (c) VLBA images at 8.4 (top left), 15.3 (top right), and 22.2 GHz (bottom) from epoch 3. In each case the bottom contour is 0.1 mJy/beam increasing in factors of 2. The data have been weighted with Briggs' weighting scheme (Briggs 1995) using a robustness parameter of 0. (d) VLBA images at 8.4 (top left), 15.3 (top right), and 22.2 GHz (bottom) from epoch 4. In each case the bottom contour is 0.1 mJy/beam increasing in factors of 2. The data have been weighted with Briggs' weighting scheme (Briggs 1995) using a robustness parameter of 0.
Download figure:
Standard image High-resolution image3.1. Nuclear Structure
Figure 4 shows the 43.1 GHz VLBA images from the four epochs. The components K2 and K3 are the new ejections that are partially resolved in epochs 1 and 4. Detecting these putative ejections was a major goal of these observations. As noted earlier, the higher sensitivity observations afforded by the new VLBA backend systems improved the ability to phase-reference and detect these ejecta compared to our 2006 observations. The new component could not be detected in epochs 2 and 3, due to an unfortunate beam shape elongated along the jet direction: the direction that needs the highest resolution in order to resolve new components ejected from the core. The ejected component flux density in the two epochs is only 2–3 mJy. We identify the partially resolved component in epochs 1 and 4 as K2 and K3, respectively.
Figure 4. Naturally weighted VLBA images at 43.1 GHz. The top row from left to right shows epochs 1 and 2. The bottom row from left to right show epochs 3 and 4. The bottom contour is at 0.085 mJy/beam in each case and contours increase in factors of 2. The crosses and ellipses with inscribed crosses denote the locations of point source components and the locations and dimensions of the Gaussian elliptical components, respectively. Note that the major axis of the elliptical Gaussian model for the core tends to point along the jet direction. It is also very elongated in this direction during the earlier stages of the flare.
Download figure:
Standard image High-resolution imageEven though a large amount of information was lost due to poor resolution along the jet direction in epochs 2 and 3, we did anticipate the additional information that can be found in the core spectrum with a multifrequency observation plan. This aspect was achieved as all 10 VLBA stations successfully observed in all epochs. The spectra of the unresolved core in each epoch are shown in Figure 5. In Reynolds et al. (2009), we used the detailed nature of the spectral shape to argue that the spectrum of the radio core was most likely a power-law synchrotron spectrum that was seen through an SSA screen as opposed to a synchrotron power-law spectrum that was seen through an opaque screen caused by free–free absorption. The spectrum in epoch 1 is consistent with this interpretation.
Figure 5. Spectrum of the unresolved radio core in the four epochs. The data are from Table 1. The continuous curves are SSA power-law fits to the data. We have also added the flux density of the 2006.32 unresolved nucleus for historical reference to the flare described in Reynolds et al. (2009).
Download figure:
Standard image High-resolution imageThe plots in Figure 5 show the synchrotron self-absorbed (SSA) power-law fits to the first three epochs—a simple spectral model has been used to describe previous observations (Reynolds et al. 2009). The first two epochs have surprisingly similar spectra and fits. The spectral index is  , and the SSA optical depth is unity at 11.2 GHz (where α is defined in terms of flux density as
, and the SSA optical depth is unity at 11.2 GHz (where α is defined in terms of flux density as  ). The third epoch has
). The third epoch has  and an optical depth of unity at 10.4 GHz. The trend is ostensibly that which would be expected as a source expands (adiabatic cooling) and/or is synchrotron cooled or is Compton cooled by accretion-disk photons. In this scenario, the peak emission should shift to lower and lower frequency and the spectrum should steepen at high frequency (the highest energy electrons cool first) (Ginzburg & Syrovatskii 1969; Moffet 1975; Tucker 1975). Oddly, epoch 4 is a pure power law with no turnover due to SSA absorption and
and an optical depth of unity at 10.4 GHz. The trend is ostensibly that which would be expected as a source expands (adiabatic cooling) and/or is synchrotron cooled or is Compton cooled by accretion-disk photons. In this scenario, the peak emission should shift to lower and lower frequency and the spectrum should steepen at high frequency (the highest energy electrons cool first) (Ginzburg & Syrovatskii 1969; Moffet 1975; Tucker 1975). Oddly, epoch 4 is a pure power law with no turnover due to SSA absorption and  . There is a fundamental physical change in the nucleus between epochs 3 and 4. The most curious aspect of epoch 4, considering the fading of the flare, is that the spectrum is relatively flat. It seems to represent a disjoint epoch of low-level power-law emission that supersedes the cooling plasmoid phase that occurs between epochs 2 and 3. We have included the nuclear flux densities from the 2006.32 flare that were given in Reynolds et al. (2009) for comparison purposes. In the context of a simple SSA power-law model, the nucleus was more self-absorbed in 2006 with a steeper power-law spectral index.
. There is a fundamental physical change in the nucleus between epochs 3 and 4. The most curious aspect of epoch 4, considering the fading of the flare, is that the spectrum is relatively flat. It seems to represent a disjoint epoch of low-level power-law emission that supersedes the cooling plasmoid phase that occurs between epochs 2 and 3. We have included the nuclear flux densities from the 2006.32 flare that were given in Reynolds et al. (2009) for comparison purposes. In the context of a simple SSA power-law model, the nucleus was more self-absorbed in 2006 with a steeper power-law spectral index.
Perhaps the most unexpected finding is that the nuclear spectrum is unchanged within the measurement accuracy of the VLBA between epochs 1 and 2. In 18 days, there was no change in the spectrum, yet the light curve shows a 20 mJy peak-to-peak variation at 17.6 GHz in the intervening time frame. Presumably, considering the size of the error bars on the AMI data, it is quite possible that the intrinsic flux was actually quite stable during this time frame and possibly even back to the middle of 2015 March, with only a few mJy variation (approximately 205–210 mJy) and the triggering observation on 2016 March 27 (216 mJy) was a statistically extreme variation arising from systematic errors. This is the only consistent explanation of the combined AMI and VLBA data from mid-March to mid April. The implication is there was a broad one-month plateau in the light curve that corresponded to a sustained epoch of jet activity. With this interpretation, it is very evident from the AMI light curve in Figure 2 that a new epoch of jet behavior, which is more variable with larger flux densities of 225–240 mJy, commences immediately after the epoch 2 VLBA observation. The interpretation of the peak of jet activity during the 2015 flare as two distinct plateaus is illustrated in Figure 6. VLBA epochs 1 and 2 are in the middle and end of plateau 1, respectively. This could explain the similar core spectra in Figure 5. There is no observation during plateau 2. The VLBA observation in epoch 3 appears to be during the very beginning of the decay of the more luminous plateau 2. Unfortunately, there was no AMI data available near the time of the epoch 4 observation or afterward.
Figure 6. Close-up of the active plateau regions of the light curve. These are the high states associated with the peak of jet activity.
Download figure:
Standard image High-resolution image3.2. Ejected Components
An important diagnostic of the jet activity near the source is provided by component motion. We can improve on the inherent astrometric accuracy provided by our phase-referenced observations by using the position of component K1 as a reference point. This is a very stationary feature. In the two epochs observed in Reynolds et al. (2009), 2006.07 and 2006.32, the distance from the core to K1 at 43 GHz was 1.222 and 1.216 mas. In the four epochs observed in this program, the separations at 43.1 GHz, were 1.230, 1.212, 1.192, and 1.247 mas in temporal order, with an average of 1.220 mas. This equates to  mas of motion in nine years. Thus, with excellent precision, we consider K1 to be a fixed origin for our astrometric coordinates. We will explain the fluctuations in this separation during our four observations in the following discussion. They are likely related to beam shape and nuclear activity.
mas of motion in nine years. Thus, with excellent precision, we consider K1 to be a fixed origin for our astrometric coordinates. We will explain the fluctuations in this separation during our four observations in the following discussion. They are likely related to beam shape and nuclear activity.
In contrast, the core is not a reliable origin for determining component motion. This is not due to SSA opacity effects as traditionally considered in homogeneous jet models (Blandford & Königl 1979). The spectrum is indicative of optically thin plasma at 43.1 GHz in epochs 1–3. It is likely that resolution as a consequence of beam shape and size will determine how much of the optically thin emission is represented in the 43.1 GHz core. In this context, it is important to recognize that there are likely multiple discrete ejections that are unresolved by the VLBA at 43.1 GHz. We can infer this from two pieces of evidence. First, there are the abrupt jumps in 17.6 GHz flux density that occur in the AMI light curve in Figure 2. Second, the Gaussian elliptical fits to the 43.1 GHz core in Table 1 are characterized by a major axis that is very elongated, with a minor axis more than half a beam width. The major axis is approximately parallel to the direction to the stationary component, K1. Considering the detection of two ejected components K2 and K3 and the abrupt jumps in the light curve, the existence of multiple components along the jet direction are a natural explanation of the 43.1 GHz Gaussian fits to the unresolved core that are highly elongated along the jet direction. This interpretation of the nuclear fits is consistent with the core position shift that is evident in Figure 7 from epoch to epoch. Depending on the distribution and brightness of these ejecta, the centroid of the unresolved beam will move. Consider the motion of the 43.1 GHz radio core in Figure 7. In this plot, all of the coordinates are based on making the unresolved, stationary component K1 the true origin for astrometry. Notice that the core moves along the jet toward K1 at epoch 2. The reason is likely twofold. First, there are possible new unresolved ejecta that might be manifested as modulations of the light curve in Figures 2 and 6. Second, the elongation of the beam shape along the jet direction inhibits the resolution of new and older weak components that have been ejected (i.e., the component K2 from epoch 1 cannot be resolved by this beam). This inability to resolve ejecta that are directed toward K1 will result in a shift of the centroid of the core emission toward K1. The same effect occurs in epoch 3 as the poor resolution along the jet direction is unable to resolve the relatively strong new ejection, K3. This is likely the cause of the shift of the core position to its closest point toward K1. As the core becomes less active during the fading of the flare after epoch 3, the core drifts away from K1 as the ejecta are fewer and weaker and therefore contribute less to the unresolved base of the jet. The motion between epochs 3 and 4 is exaggerated by the elongated beam along the jet direction in epoch 3. The smaller beam along the jet direction in epoch 4 resolves out another component, which we call K3. Thus, we consider the core position in epoch 4 our best estimate of the active galactic nucleus (AGN) because it is based on a high-resolution observation along the jet direction, and the observation is during a state of decline of the 17.6 GHz radio flare and therefore is less likely to be unresolved, strong, new components.
Figure 7. Position of the core and the ejection relative to the astrometric origin K1.
Download figure:
Standard image High-resolution imageIn the absence of sufficient resolution to track component motion in epochs 2 and 3, we use the location of the core in the relatively quiescent epoch 4 (the AGN location) in order to constrain the apparent velocity of the components. We note that the shift of the core in epoch 4 to the position depicted in Figure 7 might be conservative. The jet spectrum in epoch 4 is flat,  . Thus, the jet might be optically thick. Therefore, due to SSA opacity, the true core position would be slightly upstream (to the left in Figure 7) from the epoch 4 core position. Extrapolating the shift by fitting the SSA core shift over frequency is logistically difficult. However, one can use the stationary secondary position as a nearby reference point in order to register the location of the core as a function of frequency in epoch 4. The first attempt did not work, because the 22.2 GHz core position was very far from the power-law fit to the other three points. We attribute this to the ejected component K3 that is unresolved in the 22.2 GHz beam. Assuming a steep power law and a large SSA opacity at 15.3 GHz, we associated 5 mJy at the position of K3 with the unresolved core at 22.2 GHz and
. Thus, the jet might be optically thick. Therefore, due to SSA opacity, the true core position would be slightly upstream (to the left in Figure 7) from the epoch 4 core position. Extrapolating the shift by fitting the SSA core shift over frequency is logistically difficult. However, one can use the stationary secondary position as a nearby reference point in order to register the location of the core as a function of frequency in epoch 4. The first attempt did not work, because the 22.2 GHz core position was very far from the power-law fit to the other three points. We attribute this to the ejected component K3 that is unresolved in the 22.2 GHz beam. Assuming a steep power law and a large SSA opacity at 15.3 GHz, we associated 5 mJy at the position of K3 with the unresolved core at 22.2 GHz and  mJy in the unresolved core at 15.3 and 8.4 GHz. We re-register the 22.2 GHz core position on the basis of the unresolved component, K3, being extricated. The resultant power-law trend is plotted in the top frame of Figure 8 and extrapolated to high frequency. It is a plot that fits a core position in decl. and R.A. with a power law for the associated core shift from this position as a function of frequency. This is an empirical process, and the expectation is that the shift from the true core position is zero at high frequency where the SSA opacity is very small. The results are plotted in Figure 8 and indicates a 0.03 mas shift of the true core position based on SSA opacity effects. The top frame is the fit to the core shift, and the bottom frame is a close-up of the core evolution and core shift resulting from this SSA opacity analysis. The SSA shifted core position in epoch 4 will be denoted as the AGN location.
mJy in the unresolved core at 15.3 and 8.4 GHz. We re-register the 22.2 GHz core position on the basis of the unresolved component, K3, being extricated. The resultant power-law trend is plotted in the top frame of Figure 8 and extrapolated to high frequency. It is a plot that fits a core position in decl. and R.A. with a power law for the associated core shift from this position as a function of frequency. This is an empirical process, and the expectation is that the shift from the true core position is zero at high frequency where the SSA opacity is very small. The results are plotted in Figure 8 and indicates a 0.03 mas shift of the true core position based on SSA opacity effects. The top frame is the fit to the core shift, and the bottom frame is a close-up of the core evolution and core shift resulting from this SSA opacity analysis. The SSA shifted core position in epoch 4 will be denoted as the AGN location.
Figure 8. Top frame shows the shift of the core as a function of frequency in epoch 4 due to SSA opacity effects. The fits of the power laws to the data are good as evidenced by the large squared multiple regression values, R2. The quantity, x, in the equation for the core shift is the observed frequency in GHz. The bottom frame shows the shifted true core location that is consistent with zero offset at high frequency in the top frame.
Download figure:
Standard image High-resolution imageBased on the shifted core position in Figure 8, we can estimate the velocity of the component K2. We know that component K2 was ejected after the flare start (after 2014 December 1; see Figures 1 and 2). It moved 0.40 ± 0.04 mas from the AGN in  days. Using a conversion of 1 mas = 0.8 pc, this equates to an apparent velocity
days. Using a conversion of 1 mas = 0.8 pc, this equates to an apparent velocity  for K2. This is a lower bound because there were likely numerous other mini-flares (associated with local maxima) during the rise of the light curve as discussed above. It is probably more likely that one of these mini-flares during the flare rise is associated with the ejection of the detected component K2. The 17.6 GHz light curve seems to indicate that the 2015 radio flare in Mrk 231 was composed of multiple small superluminal ejections.
for K2. This is a lower bound because there were likely numerous other mini-flares (associated with local maxima) during the rise of the light curve as discussed above. It is probably more likely that one of these mini-flares during the flare rise is associated with the ejection of the detected component K2. The 17.6 GHz light curve seems to indicate that the 2015 radio flare in Mrk 231 was composed of multiple small superluminal ejections.
The component K3 is located 0.26 ± 0.04 mas from the AGN. However, due to the poor beam shape in epochs 2 and 3, we have no reliable means of constraining the velocity of K3. Finally, we note that the trajectories for K2 (PA = −117°) and K3 (PA = −137°) appear to be different. K2 appears to be on a trajectory headed toward the steep spectrum secondary, K1. Component K3 curiously lies below a common line in Figure 7 that connects all the core positions and the discrete components, K1 and K2. Reprocessing the data multiple times consistently found that K3 lies to the south of this line.
3.3. The Stationary Secondary
If we assign the AGN location to the core at epoch 4, then as discussed above, the component K1 moved  mas in nine years, which is consistent with zero velocity with our level of measurement accuracy. However, if we converted this to a velocity, it would equal 4200 km s−1, which is too small for us to measure accurately. In Reynolds et al. (2009), we noted that matched (to 5 GHz) resolution VLBA observations indicated that the secondary is seen through a shroud of free–free absorbing gas with an emission measure of
mas in nine years, which is consistent with zero velocity with our level of measurement accuracy. However, if we converted this to a velocity, it would equal 4200 km s−1, which is too small for us to measure accurately. In Reynolds et al. (2009), we noted that matched (to 5 GHz) resolution VLBA observations indicated that the secondary is seen through a shroud of free–free absorbing gas with an emission measure of  . It was concluded that the steep spectrum secondary seems to be a radio lobe associated with the jet advancing into a dense medium (the jet is confined by ram pressure) that is also the source of the free–free absorption. It was estimated that the long-term time-averaged kinetic energy flux deposited in the stationary secondary is
. It was concluded that the steep spectrum secondary seems to be a radio lobe associated with the jet advancing into a dense medium (the jet is confined by ram pressure) that is also the source of the free–free absorption. It was estimated that the long-term time-averaged kinetic energy flux deposited in the stationary secondary is  erg
erg  .
.
Figure 9 compares the spectrum of component K1 in our four epochs of observation to the historical spectra presented in Reynolds et al. (2009). The flux has approximately doubled in the last nine years. This is consistent with the interpretation of K1 that it is a radio lobe confined by a dense medium. The light curve in Figures 1 and 2 indicates increased radio activity since 2011. The cumulative effect is to energize the radio lobe with more high-energy plasma. There even appears to be an additional  increase in the 8.4 GHz flux density during our observing program between epochs 1 and 3 according to Table 1. This is apparently real since the secondary calibrator J1311+5513 does not show the same increase. If we associate the increase with the plasma deposited in the lobe by the strong 2013 flare, then according to Figure 1 the time of flight from the nucleus to K1 at epoch 3 is 1.7–2.5 years. However, the flux increase at 8.4 GHz is basically a linear rise from epoch 1 to epoch 3 (see Table 1). Thus, the time that elapsed between the 2013 flare and epoch 1 is
increase in the 8.4 GHz flux density during our observing program between epochs 1 and 3 according to Table 1. This is apparently real since the secondary calibrator J1311+5513 does not show the same increase. If we associate the increase with the plasma deposited in the lobe by the strong 2013 flare, then according to Figure 1 the time of flight from the nucleus to K1 at epoch 3 is 1.7–2.5 years. However, the flux increase at 8.4 GHz is basically a linear rise from epoch 1 to epoch 3 (see Table 1). Thus, the time that elapsed between the 2013 flare and epoch 1 is  years. This time frame covers the rise of the 2013 flare to the small flare during the light curve decay of the 2013 flare. The peak of the 2013 flare was 1.9–2.0 years before the epoch 1 observation. The projected distance on the sky plane between the core and K1 is 3.2 lt-yr. The apparent speed that the energy flux propagated with is (3.2 lt-yr/2.3 year)
years. This time frame covers the rise of the 2013 flare to the small flare during the light curve decay of the 2013 flare. The peak of the 2013 flare was 1.9–2.0 years before the epoch 1 observation. The projected distance on the sky plane between the core and K1 is 3.2 lt-yr. The apparent speed that the energy flux propagated with is (3.2 lt-yr/2.3 year)  (3.2 lt-yr/1.5 year), or
(3.2 lt-yr/1.5 year), or  , consistent with mildly relativistic motion. In this scenario, based on the estimate of the velocity of the component, K2, in the last section, this value decreases as the jet propagates toward K1. This can occur if the line of sight to the jet increased dramatically or there was deceleration of the flow. A change in the line of sight is inconsistent with the tight alignment of components, and the core shifts with the direction from the core to K1 in Figure 7. This favors deceleration, which was suggested to occur by entrainment in the dense nuclear environment of Mrk 231 (Reynolds et al. 2009). Alternatively, if the increase of flux in K1 is from the 2015 flare,
, consistent with mildly relativistic motion. In this scenario, based on the estimate of the velocity of the component, K2, in the last section, this value decreases as the jet propagates toward K1. This can occur if the line of sight to the jet increased dramatically or there was deceleration of the flow. A change in the line of sight is inconsistent with the tight alignment of components, and the core shifts with the direction from the core to K1 in Figure 7. This favors deceleration, which was suggested to occur by entrainment in the dense nuclear environment of Mrk 231 (Reynolds et al. 2009). Alternatively, if the increase of flux in K1 is from the 2015 flare,  . Neither scenario is ruled out by the data. Using the K1 radio lobe as a crude bolometer indicates that the jet in Mrk 231 is becoming more energetic. Mrk 231 might be transforming from an RQQ to a radio-loud quasar.
. Neither scenario is ruled out by the data. Using the K1 radio lobe as a crude bolometer indicates that the jet in Mrk 231 is becoming more energetic. Mrk 231 might be transforming from an RQQ to a radio-loud quasar.
Figure 9. Historic spectrum of the stationary component K1.
Download figure:
Standard image High-resolution image3.4. Summary of the Subparsec-scale Radio Structure
In this section we used four epochs of VLBA observations in order to constrain the morphology and time evolution of the subparsec-scale nuclear region during the major radio flare of 2015. The first result, in Section 3.1, was the detection of partially resolved substructure at 43 GHz in epochs 1 and 4. We interpret these as ejecta associated with the major flare. The lack of the detection of substructure in epochs 2 and 3 is likely a consequence of a poorly shaped beam that reduced the resolution along the jet direction. This hindered our efforts to follow the time evolution of the ejected components. In the absence of these data, we relied on determining a precise location of the actual AGN in order to constrain the jet speed in Section 3.2. This required a careful analysis of all four data sets. We determined a lower bound on the apparent speed of the ejection that was detected in epoch 1,  . In Section 3.3, we showed that the stationary secondary (the putative radio lobe) doubled in 8.4 GHz flux density over nine years. We even detected a flux increase during this observing program. By associating this flux increase with energy from the 2013 radio flare, we estimate an average apparent jet speed of
. In Section 3.3, we showed that the stationary secondary (the putative radio lobe) doubled in 8.4 GHz flux density over nine years. We even detected a flux increase during this observing program. By associating this flux increase with energy from the 2013 radio flare, we estimate an average apparent jet speed of  . Alternatively, if the increase of flux in the stationary secondary is from the present flare,
. Alternatively, if the increase of flux in the stationary secondary is from the present flare,  . Neither scenario is ruled out by the data.
. Neither scenario is ruled out by the data.
4. The Far-UV Jet Connection
In this section, we explore the possible relationships between the far-UV spectrum and the radio state of the nucleus.
4.1. The Timing of the Flare Initiation and the HST COS G140L Observation
The 2014 December 13 HST COS G140L observation was less than 36 hr before the first detected onset of flare activity on 2014 December 15, as evidenced by the 17.6 GHz light curve in Figures 1 and 2. From 2014 November 15 until 2014 December 7, the 17.6 GHz flux density was in a slow monotonic decline from 132 to 127 mJy. The next data point (MJD 57007) was eight days later, and the flux density increased to 142 mJy. This increase was not a statistical fluctuation or systematic observational error since the light curve showed steady growth afterwards (except for one outlier point in bad weather 29 days later). Furthermore, the spectral index from 14.6 to 17.6 GHz showed a linear decrease (spectral flattening) from MJD 56985 until MJD 57019, going from  to
to  (see the top frame of Figure 10). The spectral index has a large uncertainty and using 14.6 GHz for our low frequency instead of 13.8 GHz is much more reliable with AMI data. However, there is a consistent trend of spectral hardening that is evident more than a week before the 17.6 GHz flux density begins to increase and for 12 days afterwards.
(see the top frame of Figure 10). The spectral index has a large uncertainty and using 14.6 GHz for our low frequency instead of 13.8 GHz is much more reliable with AMI data. However, there is a consistent trend of spectral hardening that is evident more than a week before the 17.6 GHz flux density begins to increase and for 12 days afterwards.
Figure 10. Beginning of the major radio flare that peaked in the spring of 2015. The top frame plots the total flux density from the AMI data. The spectral index has a large uncertainty. However, there is a consistent trend of spectral hardening that is evident more than a week before the 17.6 GHz flux density begins to increase and for 12 days afterwards. The bottom frame describes the implied change to the nuclear component using Equations (1)–(4) in the text. The spectrum hardens dramatically a few days days to two weeks before the G140L observation. The implication is that the flux was increasing at high frequency during this time period. As the disturbance propagates away from the nucleus, the SSA opacity decreases. Around the time of the G140L observations, the spectrum begins to soften and the 17.6 GHz flux density starts to increase rapidly, increasing by a factor of 4 in less than three weeks.
Download figure:
Standard image High-resolution imageThe changes to the nucleus would have been profound because the preponderance of the 17.6 GHz flux is from the stationary secondary and the surrounding large-scale radio emission (Ulvestad et al. 1999a). We can estimate these two background components. In order to determine the flux density of the stationary secondary,  , we note the increase of the flux density during the first three epochs of our VLBA program, which was discussed in the last section. This increase was much larger at 8.4 GHz than at 15.3 GHz. Thus, we expect a different time dependence for different frequencies. We estimate the flux densities at 14.6 and 17.6 GHz in the four VLBA epochs by extrapolating the 15.3 GHz flux density using the two point spectral indices to 8.4 and 22.2 GHz. We find at 14.6 GHz that
, we note the increase of the flux density during the first three epochs of our VLBA program, which was discussed in the last section. This increase was much larger at 8.4 GHz than at 15.3 GHz. Thus, we expect a different time dependence for different frequencies. We estimate the flux densities at 14.6 and 17.6 GHz in the four VLBA epochs by extrapolating the 15.3 GHz flux density using the two point spectral indices to 8.4 and 22.2 GHz. We find at 14.6 GHz that  (ν = 14.6 GHz) = 99 mJy, 104 mJy, and 111 mJy in epochs 1, 2, and 3, respectively. Similarly, we find at 17.6 GHz that
(ν = 14.6 GHz) = 99 mJy, 104 mJy, and 111 mJy in epochs 1, 2, and 3, respectively. Similarly, we find at 17.6 GHz that  (ν = 17.6) GHz = 74 mJy, 80 mJy, and 83 mJy in epochs 1, 2, and 3, respectively. We fit these data by power laws in time and extrapolate back to the time of the HST G140L observation:
(ν = 17.6) GHz = 74 mJy, 80 mJy, and 83 mJy in epochs 1, 2, and 3, respectively. We fit these data by power laws in time and extrapolate back to the time of the HST G140L observation:

We can find the background large-scale flux density,  , using the simultaneous VLA and VLBA observations in December 1996 (Ulvestad et al. 1999a). Being large-scale in nature (∼100 pc), these fluxes should be steady over 20 years. The VLBA images only the core and the stationary secondary with combined flux densities of 132 mJy and 63 mJy at 8.4 GHz and 15.4 GHz, respectively. The VLA is sensitive to larger-scale structures and detected flux densities of 203 mJy and 112 mJy at 8.4 GHz and ;15.4 GHz, respectively. Subtracting the VLBA flux from the VLA flux yields
, using the simultaneous VLA and VLBA observations in December 1996 (Ulvestad et al. 1999a). Being large-scale in nature (∼100 pc), these fluxes should be steady over 20 years. The VLBA images only the core and the stationary secondary with combined flux densities of 132 mJy and 63 mJy at 8.4 GHz and 15.4 GHz, respectively. The VLA is sensitive to larger-scale structures and detected flux densities of 203 mJy and 112 mJy at 8.4 GHz and ;15.4 GHz, respectively. Subtracting the VLBA flux from the VLA flux yields

Fitting the data in Equation (2) by a power law with spectral index of  , these flux densities can be used to extrapolate an estimate of the desired result:
, these flux densities can be used to extrapolate an estimate of the desired result:

The core flux,  , can be estimated from the AMI-measured flux density,
, can be estimated from the AMI-measured flux density,  , using
, using

We can check Equation (4) during the first two epochs of VLBA observations at 17.6 GHz. Recall that  (ν = 17.6 GHz) = 74 and 80 mJy from above in epochs 1 and 2. The extrapolated core flux is
(ν = 17.6 GHz) = 74 and 80 mJy from above in epochs 1 and 2. The extrapolated core flux is  in both epochs. Thus, using Equations (3) and (4) predicts that
in both epochs. Thus, using Equations (3) and (4) predicts that  ≈ 45 + 90 + 74 mJy = 209 mJy in epoch 1 and Fν(ν = 17.6 GHz) ≈ 45 + 90 + 80 mJy = 215 mJy in epoch 2, which is consistent with the levels measured (quasi-simultaneously) during plateau 1 in Figure 6. With the confidence provided by this consistency check, we estimate
≈ 45 + 90 + 74 mJy = 209 mJy in epoch 1 and Fν(ν = 17.6 GHz) ≈ 45 + 90 + 80 mJy = 215 mJy in epoch 2, which is consistent with the levels measured (quasi-simultaneously) during plateau 1 in Figure 6. With the confidence provided by this consistency check, we estimate  from the AMI light curve in the bottom frame of Figure 10. Note that the estimated
from the AMI light curve in the bottom frame of Figure 10. Note that the estimated  increases from 14 to 30 mJy at the time of the HST observation and the spectral index is extremely inverted and a short extrapolation to 22.2 GHz implies that
increases from 14 to 30 mJy at the time of the HST observation and the spectral index is extremely inverted and a short extrapolation to 22.2 GHz implies that  mJy. The bottom frame of Figure 10 indicates that the nuclear spectrum hardens dramatically a few days to two weeks before the G140L observation. A hardening of the spectrum is expected before the rise of the low-frequency flux in the early stages of an optically thick flare. The implication is that the flux was increasing at high frequency during this time period. As the ejected plasma propagates to larger dimension, the SSA opacity decreases. Around the time of the G140L observations, the spectrum begins to soften and the SSA opacity is sufficiently low at 17.6 GHz that the flux density starts to increase rapidly, increasing by a factor of 4 in less than three weeks.
mJy. The bottom frame of Figure 10 indicates that the nuclear spectrum hardens dramatically a few days to two weeks before the G140L observation. A hardening of the spectrum is expected before the rise of the low-frequency flux in the early stages of an optically thick flare. The implication is that the flux was increasing at high frequency during this time period. As the ejected plasma propagates to larger dimension, the SSA opacity decreases. Around the time of the G140L observations, the spectrum begins to soften and the SSA opacity is sufficiently low at 17.6 GHz that the flux density starts to increase rapidly, increasing by a factor of 4 in less than three weeks.
The conclusion is that the elevated flux on 2014 December 15 (MJD 57005.5) is a direct consequence of the flare that peaked six months later. Because of the gap in observations between 2014 December 8 and 15, the light curve could have begun a drastic increase at any time in between. Furthermore, for an optically thick flare at 17.6 GHz, the 43 GHz flux density increase leads (in time) the increase of the 17.6 GHz flux density. Thus, the 2014 December 13 HST COS G140L observation was most likely a few days to two weeks after the flare initiated.
4.2. Previous HST Observations
Another observation that occurred during an active radio state was the HST COS G130M observation on 2011 October 15 that was indicated in the top frame of Figure 1. Figure 11 is a magnified view of the radio flare so that one can see the radio state at the time of the HST observation. Note that the observation was during a very high 22 GHz flux state. The flare was experiencing a saddle point that was either near the peak of the flare or on the declining side. It appears that both the G140L and the G130M observations occurred during very active jet states, at the start of a strong flare and during the last local maximum of another strong flare, respectively. Conversely, as discussed in terms of Figure 1, the 1996 November 21 HST FOS spectrum was taken near (within two weeks of) a historic low in the 22 GHz radio flux.
Figure 11. HST COS G130M observation during the 2011 radio flare.
Download figure:
Standard image High-resolution imageThere is a great disparity between the quality of the FOS and COS data sets. The highest quality data are the G130M data from 2011. It is averaged over 10 observations that exceed a total of 12,000 s. These data were previously discussed in Veilleux et al. (2013, 2016) and the averaged data was generously provided by S. Veilleux and M. Melendez. However, these data had a rather narrow wavelength coverage. The G140L spectrum from 2014 was downloaded from the Milkulski Archive for the Space Telescope (MAST) and is of comparable quality with over 15,000 s of observation, but with a much wider wavelength range and much lower spectral resolution. These data have been considered extensively in Veilleux et al. (2016). The FOS G160L data was a short 770 s exposure with low resolution. The following discussion is highly dependent on this brief observation. The important aspect for this discussion is knowing if the absolute flux calibration was accurate. In order to remove ambiguity, we excised the spectrum below 1315 Å in order to avoid Geo OI coronal emission and Geo Lyα emission that is impossible to reliably extricate with the low resolution combined with the noisy edge of the spectral coverage. With these issues removed, we can assess the flux calibration. The observation was post-COSTAR and the acquisition method was ACQ/PEAK that creates a centering uncertainty of 0 05 (Evans & Koratkar 2004). This equates to a 1% flux uncertainty in the 1
05 (Evans & Koratkar 2004). This equates to a 1% flux uncertainty in the 1 0 circular aperture (FOS Instrument Science Reports CAL/FOS-140) that was used. The data acquisition files had no flags or warnings, so every indication is that the flux uncertainty should be
0 circular aperture (FOS Instrument Science Reports CAL/FOS-140) that was used. The data acquisition files had no flags or warnings, so every indication is that the flux uncertainty should be  (Evans & Koratkar 2004). The absolute flux density of the COS observations is likely better. The 10 different observations with G130M agree within
(Evans & Koratkar 2004). The absolute flux density of the COS observations is likely better. The 10 different observations with G130M agree within  in the overlapping ranges of wavelength, similarly for the two observations with G140L.
in the overlapping ranges of wavelength, similarly for the two observations with G140L.
4.3. Comparing the Three Epochs of HST Observations
The far-UV spectra are compared in Figure 12 by plotting each pair of SEDs in different panels. Plotting all three at once is too cluttered for comparative purposes. There are some amazing similarities and striking contrasts that are catalogued in Table 2. The top frame in Figure 12 compares the two SEDs that were sampled when the radio jet was in a state of high activity. There is no observable difference in the region of overlap between 1150 and  . The Geo OI coronal emission and Geo Lyα emission were left in for reference in the higher spectral resolution G130M SED. These regions were excised from the G140L SED for clarity. The spectral index of
. The Geo OI coronal emission and Geo Lyα emission were left in for reference in the higher spectral resolution G130M SED. These regions were excised from the G140L SED for clarity. The spectral index of  in column (8) of Table 2 for the continuum flux density,
in column (8) of Table 2 for the continuum flux density,  , between 1315 and 1050 Å agrees with the value found previously for the G130M spectrum (Veilleux et al. 2013). Formally, the spectral coverage ends at
, between 1315 and 1050 Å agrees with the value found previously for the G130M spectrum (Veilleux et al. 2013). Formally, the spectral coverage ends at  , so the last
, so the last  is an extrapolation. The G140L spectrum shows a spectral break near
is an extrapolation. The G140L spectrum shows a spectral break near  .
.
Figure 12. Top panel compares the SEDs of the two high-radio states, the 2011 flare and the 2015 flare. The middle panel compares the SED during the 2015 flare and during the radio-low state in 1996. There is C iv BAL absorption and a harder spectrum in 1996. The last frame compares the SED in 1996 and during the radio flare in 2011. The SEDs diverge shortward of  .
.
Download figure:
Standard image High-resolution imageTable 2. Far-UV Spectral Properties vs. High-frequency Radio Properties
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|
| Date | 17.6 GHz | 22 GHz | Date | Grating/ |

|

|
 a
a
|
 b
b
|
BALnicity |
| Flux | Flux | ||||||||
| Radio | Density | Density | HST | Spectro- | 10−15 | 10−15 | C iv | ||
| Obs. | (mJy) | (mJy) | Obs. | graph | erg  
|
erg  
|
(km s−1) | ||
| 1996 Dec 05 | 90 ± 10c | 62 ± 9 | 1996 Nov 21 | FOS/G160L | 168 ± 17 | 128 ± 13 | ... |

|
 d
d
|
| 2011 Sep 30 | ... | 200 ± 10 | 2011 Oct 15 | COS/G130M | 139 ± 7 | ... | 1.7 | ... | ... |
| 2011 Oct 25 | ... | 180 ± 5 | 2011 Oct 15 | COS/G130M | 139 ± 7 | ... | 1.7 | ... | ... |
| 2014 Dec 15 | 142 ± 5 | ... | 2014 Dec 13 | COS/G140L | 140 ± 7 | 135 ± 7 | 1.5 | −0.1 | 0e |
Notes.
aSpectral index of the continuum power law, . Computed from 1050 to
. Computed from 1050 to  .
bSpectral index of the continuum power law,
.
bSpectral index of the continuum power law,  . Computed from 1315 to
. Computed from 1315 to  .
cEstimated from the VLA data in Ulvestad et al. (1999a).
dGallagher et al. (2002).
eVeilleux et al. (2016).
.
cEstimated from the VLA data in Ulvestad et al. (1999a).
dGallagher et al. (2002).
eVeilleux et al. (2016).
Download table as: ASCIITypeset image
The middle frame compares the high-activity jet state at the beginning of the 2015 flare and the 1996 low-radio luminosity state. The SED is very similar from 1400 to  , even after 18 years. However, shortward of
, even after 18 years. However, shortward of  there is a clear visual excess in the 1996 SED. We would like to quantify what we see visually. One method was to compute the integrated flux in two bands,
there is a clear visual excess in the 1996 SED. We would like to quantify what we see visually. One method was to compute the integrated flux in two bands,  in column (6) of Table 2 and in the range
in column (6) of Table 2 and in the range  in column (7) of Table 2. Even though the flux in the band
in column (7) of Table 2. Even though the flux in the band  is slightly larger in 2014, it is significantly smaller in the band
is slightly larger in 2014, it is significantly smaller in the band  in 2014. Visually, it is very clear in the figure that the G140L SED angles downward toward shorter wavelength between 1315 and 1900 Å. However, the data are inconsistent with such a downward slant in 1996. We quantify this in Table 2 in column (9) with the spectral index
in 2014. Visually, it is very clear in the figure that the G140L SED angles downward toward shorter wavelength between 1315 and 1900 Å. However, the data are inconsistent with such a downward slant in 1996. We quantify this in Table 2 in column (9) with the spectral index  in 1996 (a flat SED) compared to
in 1996 (a flat SED) compared to  in 2014. The other significant distinction is the depth of the C iv BAL trough. The BALnicity index, BI, was defined in Weymann et al. (1991) as
in 2014. The other significant distinction is the depth of the C iv BAL trough. The BALnicity index, BI, was defined in Weymann et al. (1991) as

where F(v) is the flux density normalized to the continuum level as a function of v, the velocity from the QSO rest-frame line emission frequency in km s−1. The step function  if and only if there is more than 2000 km s−1 of continuous absorption beyond −3000 km s−1. This measure of broad absorption has been borne out over the years to be very robust. More lax measures of absorption (such as associated absorption and mini-BALs) have turned out to represent different classes of objects, which have less X-ray absorption than BALQSOs and larger radio luminosity than bona fide BALQSOs (Punsly 2006; Knigge et al. 2008; Shankar et al. 2008). Column (10) of Table 2 lists the estimated values of BI. During the low-radio state in 1996,
if and only if there is more than 2000 km s−1 of continuous absorption beyond −3000 km s−1. This measure of broad absorption has been borne out over the years to be very robust. More lax measures of absorption (such as associated absorption and mini-BALs) have turned out to represent different classes of objects, which have less X-ray absorption than BALQSOs and larger radio luminosity than bona fide BALQSOs (Punsly 2006; Knigge et al. 2008; Shankar et al. 2008). Column (10) of Table 2 lists the estimated values of BI. During the low-radio state in 1996,  km s−1 (Gallagher et al. 2002). At the beginning of the 2015 flare, BI = 0 km s−1 (Veilleux et al. 2016). In the middle panel of Figure 12, it is evident that there is more high velocity absorption in 1996.
km s−1 (Gallagher et al. 2002). At the beginning of the 2015 flare, BI = 0 km s−1 (Veilleux et al. 2016). In the middle panel of Figure 12, it is evident that there is more high velocity absorption in 1996.
The bottom panel of Figure 12 compares the SED during the 2011 flare and the quiescent state in 1996. Even though the overlap in spectra is only from 1315 to 1470 Å, it is clear that the SEDs agree in the range of 1400)–1470 Å, but they clearly diverge shortward of this. The long wavelength end of the G140L continuum fit is left on the plot for an additional reference level.
In summary, based on limited data and the inability to secure an HST spectra during the peak of the 2015 as a ToO, we find some trends that would need to be verified with more spectra.
- 1.The far-UV emission longward of
 is incredibly constant over an 18 year period. This finding is unusual for a quasar. Studies of far-UV variability of quasars indicate that measurable variability is the norm for these timeframes although no variability is occasionally found (Wilhite et al. 2005; Welsh et al. 2011; Macleod 2012).
is incredibly constant over an 18 year period. This finding is unusual for a quasar. Studies of far-UV variability of quasars indicate that measurable variability is the norm for these timeframes although no variability is occasionally found (Wilhite et al. 2005; Welsh et al. 2011; Macleod 2012). - 2.There is a far-UV flux deficit shortward of
 during periods of increased relativistic jet activity, relative to the far-UV flux in periods of low-radio activity.
during periods of increased relativistic jet activity, relative to the far-UV flux in periods of low-radio activity. - 3.The high-ionization BAL absorption is suppressed during periods of increased relativistic jet activity.
- 4.There is a sharp spectral break near
 during periods of high jet activity. It is unknown what happens during periods of low-radio emission. The peak of the far-UV SED is longward of
during periods of high jet activity. It is unknown what happens during periods of low-radio emission. The peak of the far-UV SED is longward of  . The spectral index shortward of
. The spectral index shortward of  ,
,  , is extremely steep and unusual for a quasar (Telfer et al. 2002).
, is extremely steep and unusual for a quasar (Telfer et al. 2002).
5. X-Ray Observations
Mrk 231 was observed three times with NuSTAR and twice with XMM-Newton during the 2015 campaign. As reported in Table 3, NuSTAR observed the source on April 2 (∼32 ks of net exposure), on April 19 (∼28 ks), and on May 28 (∼30 ks), while the two XMM-Newton observations were carried out on April 25 (∼19 ks) and on May 28 (∼21 ks). Table 3 also reports one previous XMM-Newton observation (performed on 2001 June 7) and two archival NuSTAR observations performed on 2012 August 26 and 2013 May 9 that we use for comparison purposes.
Table 3. Log of the X-ray Observations Used in this Work
| Mission | Name | Date | Detector | Net exposure |
|---|---|---|---|---|
| XMM-Newton | XMM 1 | 2001 Jun 07 | EPIC-pn | 17 ks |
| NuSTAR | NuSTAR 1 | 2012 Aug 27 | FPM (A-B) | 41 ks |
| NuSTAR | NuSTAR 2 | 2013 May 09 | FPM (A-B) | 29 ks |
| NuSTAR | NuSTAR 3 | 2015 Apr 02 | FPM (A-B) | 32 ks |
| NuSTAR | NuSTAR 4 | 2015 Apr 19 | FPM (A-B) | 28 ks |
| XMM-Newton | XMM 2 | 2015 Apr 25 | EPIC-pn | 19 ks |
| NuSTAR | NuSTAR 5 | 2015 May 28 | FPM (A-B) | 30 ks |
| XMM-Newton | XMM 3 | 2015 May 28 | EPIC-pn | 21 ks |
Download table as: ASCIITypeset image
5.1. The 2015 NuSTAR Observations
In order to assess the relevance of the five pointed observations of Mrk 231 with NuSTAR in the context of jet activity, we consult the light curve in Figures 1 and 2. More resolution is needed in Figure 1 in order to clarify the radio state for the NuSTAR 1 observation. The light curve in Figure 13 of the 2013 flare indicates that the NuSTAR 1 observation occurred during a low-radio state and the NuSTAR 2 observation occurred during a high-radio state (as did the NuSTAR 3, 4, and 5 observations in 2015). Thus, NuSTAR 1 is in a low-radio state and NuSTAR 2–5 are all in a high-radio state.
Figure 13. Light curve of the 2013 flare shows that the NuSTAR 1 observation occurred during a low-radio state and the NuSTAR 2 observation occurred during a high-radio state. As discussed in Reynolds et al. (2013b), the AMI monitoring began in the large array. However, as can be seen from the onset of some large scatter, calibration issues developed and we shifted to the small array.
Download figure:
Standard image High-resolution imageThe NuSTAR 1 low-radio state X-ray spectrum is compared with all other high-radio flux NuSTAR observations in Figure 14. We note that the NuSTAR 1 observation presents a clear deficit of X-ray photons below 12 keV with respect to the NuSTAR 2, 3 and 5 observations. This is especially noticeable bluewards of the Fe emission line (around 6 keV in the observed frame) where there are hints for absorption structures in NuSTAR 1 between 6.5 and 10 keV. The NuSTAR 1 and NuSTAR 4 spectra seem to be more similar, although some subtle difference may be present in two narrow bands around 7 and 8.5 keV. On the other hand, the high-energy spectra above ∼12 keV look the same at all epochs. These qualitative claims are confirmed by comparing the (model-independent) background-subtracted count rates in the soft and hard bands for all observations. The net count rates are reported in Table 4, and they confirm that the NuSTAR 1 observation is characterized by a deficit of soft X-ray photons with respect to the NuSTAR 2, 3, and 5 pointings. NuSTAR 4 appears to have a soft X-ray deficit similar to NuSTAR 1, while high-energy count rates above 12 keV are consistent with each other at all epochs, with perhaps a hint of decreased flux in the last NuSTAR observation. This suggests that any difference in the X-ray spectrum between epochs is likely due to intervening absorption rather than being intrinsic. The shape of the NUSTAR 1 spectrum between 6.5 and 10 keV seems indeed to suggest that some absorption feature is present in that band. This structure may be present in other observations as well, but with reduced strength.
Figure 14. Low radio-flux state NuSTAR 1 X-ray spectrum (black filled squares in all panels) is compared with all other high radio-flux NuSTAR spectra (red empty circles in all panels) in the most sensitive NuSTAR band (3–30 keV). Each spectrum is the result of co-adding the FPM A and B NuSTAR detectors, as this improves visual clarity. The co-added spectra are produced by combining source and background spectra, as well as responses using the addspec FTOOL available within the HEASOFT package. Solid lines are plotted only to guide the eye, and they step through all data points (no spectral fit is included here).
Download figure:
Standard image High-resolution imageTable 4. The Net Count Rates for All NuSTAR Observations in the 3–12 keV and 12–30 keV Bands
| Observation | 3–12 keV Count Rate | 12–30 keV Count Rate |
|---|---|---|
| NuSTAR 1 | 1.44 ± 0.05 | 0.56 ± 0.03 |
| NuSTAR 2 | 1.89 ± 0.06 | 0.61 ± 0.04 |
| NuSTAR 3 | 1.97 ± 0.06 | 0.57 ± 0.03 |
| NuSTAR 4 | 1.62 ± 0.06 | 0.54 ± 0.04 |
| NuSTAR 5 | 1.79 ± 0.06 | 0.52 ± 0.03 |
Note. Count rates are derived from the co-added A+B detectors data for all observations. Units are 10−2 cts s−1.
Download table as: ASCIITypeset image
We then proceed by fitting all available NuSTAR data in the highest signal-to-noise band, namely, the 3–30 keV one. Mrk 231 is unresolved by the NuSTAR beam, thus star formation and high mass X-ray binary emission are responsible for a non-negligible fraction of the total X-ray emission detected by NuSTAR (Teng et al. 2014). We do not want to speculate on complicated models with many uncertainties and assumptions, and we use some very simple spectral models here. The baseline model is that of a simple power-law continuum absorbed by a Galactic column density fixed at  cm−2 Kalberla et al. 2005), plus an extra absorbing column of neutral gas at the redshift of the source and a Gaussian emission line with σ fixed to 10 eV (unresolved at the resolution of the NuSTAR A and B detectors) to reproduce the Fe K emission line (the line energy is restricted between 6.4 and 6.97 keV in the rest frame). All our spectral analysis is first carried out considering the FPM A and B NuSTAR detectors separately, including a cross-normalization constant between the two. We then produce co-added spectra (A+B) for all observations, and we re-fit the co-added spectra with the same spectral model. As we do not find any statistically significant difference in any of the spectral parameters we derive, we proceed by reporting results for the co-added A+B spectra.
cm−2 Kalberla et al. 2005), plus an extra absorbing column of neutral gas at the redshift of the source and a Gaussian emission line with σ fixed to 10 eV (unresolved at the resolution of the NuSTAR A and B detectors) to reproduce the Fe K emission line (the line energy is restricted between 6.4 and 6.97 keV in the rest frame). All our spectral analysis is first carried out considering the FPM A and B NuSTAR detectors separately, including a cross-normalization constant between the two. We then produce co-added spectra (A+B) for all observations, and we re-fit the co-added spectra with the same spectral model. As we do not find any statistically significant difference in any of the spectral parameters we derive, we proceed by reporting results for the co-added A+B spectra.
All of the NuSTAR observations, except for the low-radio state NuSTAR 1 observation, are well fitted by the simple baseline model with  of the order of unity. NuSTAR 1 represents the exception, and the baseline model provides a poor fit to the data with
of the order of unity. NuSTAR 1 represents the exception, and the baseline model provides a poor fit to the data with  for 56 degrees of freedom (dof). The second worse fit is obtained for NuSTAR 4 (as expected, given that this is the observation that mostly resembles NuSTAR 1; see Figure 14), where we have
for 56 degrees of freedom (dof). The second worse fit is obtained for NuSTAR 4 (as expected, given that this is the observation that mostly resembles NuSTAR 1; see Figure 14), where we have  for 40 dof. Our results are reported in Table 5, and the peculiar NuSTAR 1 spectrum and best-fitting baseline model are shown in the left panel of Figure 15.
for 40 dof. Our results are reported in Table 5, and the peculiar NuSTAR 1 spectrum and best-fitting baseline model are shown in the left panel of Figure 15.
Figure 15. NuSTAR 1 X-ray spectrum and best-fitting baseline model shown in the left panel. The right panel presents the same data together with the best-fitting model including an ionized X-ray wind that accounts well for the deficit of photons in the 6.5–10 keV band (observed frame).
Download figure:
Standard image High-resolution imageTable 5. Baseline Model Fits to All NuSTAR Observations
| Observation | Γ | NH | EFe | IFe | χ2/dof |
|---|---|---|---|---|---|
| NuSTAR 1 | 1.20 ± 0.20 | 5 ± 4 | 6.5 ± 0.1 | 3.5 ± 2.0 | 82/56 |
| NuSTAR 2 | 1.50 ± 0.20 | 5 ± 4 |

|

|
47/45 |
| NuSTAR 3 | 1.60 ± 0.20 | 10 ± 5 | 6.55 ± 0.15 | 4.4 ± 2.3 | 54/52 |
| NuSTAR 4 | 1.40 ± 0.20 | 5 ± 4 |

|

|
58/40 |
| NuSTAR 5 | 1.50 ± 0.20 | 5 ± 4 | 6.7 ± 0.2 | 2.8 ± 1.8 | 54/45 |
Note. Column densities are expressed in units of 1022 cm−2, the Fe line energy is in keV, and its intensity is in units of 10−6 ph s−1 cm−2. Note that the Fe line is not formally detected during the NuSTAR 2 and 4 observations. (We fix its energy to 6.6 keV in order to compute an upper limit on its intensity).
Download table as: ASCIITypeset image
It is interesting to note that the only data set that is not well described by the baseline model (the NuSTAR 1 low-radio state spectrum in 2012) was used, together with a simultaneous and higher quality Chandra X-ray spectrum (and to the NuSTAR 2 data) to argue that an ultra-fast wind is present in Mrk 231. The evidence for such wind was detected in X-ray absorption from 6.5 to 10 keV (Feruglio et al. 2015). This appears to be a likely explanation for the deficit of X-ray photons in the 6.5–10 keV band during the NuSTAR 1 observation (see the left panel of Figure 15), although our analysis seems to exclude that the NuSTAR 2 observation (high-radio state) can be interpreted in a similar way. This is unlikely to represent a problem for the claimed wind detection, as the overall statistical result is dominated by the Chandra spectrum, simultaneous with NuSTAR 1. As mentioned, from a radio point of view, the NuSTAR 1 and Chandra observations were performed during a low-radio state, while NuSTAR 2 was already in a high-radio state. As the NuSTAR 2 spectrum is well described by the baseline model and does not exhibit signs for a deficit of photons in the interesting band, it is tempting to associate the presence of the wind with low-radio states.
In order to see whether the peculiarity of the NuSTAR 1 spectrum is indeed well described by an X-ray wind, we add a further ionized absorber to our spectral model for the NuSTAR 1 observation. The additional ionized absorber (modeled via the photoionization code PHASE; see Krongold et al. 2003) depends on the absorber column density, ionization, and outflow velocity as well as on the gas turbulent velocity. The latter parameter is however fixed to an intermediate value of 500 km s−1 as the poor spectral resolution of the NuSTAR data is not sufficient to constrain it.
The ionized absorber provides a statistical improvement of the fit for the NuSTAR 1 data with  for 53 degrees of freedom (dof), to be compared with
for 53 degrees of freedom (dof), to be compared with  for 56 dof of the baseline model, i.e., the ionized absorber is detected at the 99.4% confidence level according to a simple F-test. The addition of the ionized absorber produces a slightly steeper photon index for the NuSTAR 1 spectrum, which is more in line with that from all others (
for 56 dof of the baseline model, i.e., the ionized absorber is detected at the 99.4% confidence level according to a simple F-test. The addition of the ionized absorber produces a slightly steeper photon index for the NuSTAR 1 spectrum, which is more in line with that from all others ( versus
versus  with the baseline model). All other parameters are the same, within the errors, as those obtained with the baseline model. From our best-fitting model, we infer that the ionized absorber has a column density of
with the baseline model). All other parameters are the same, within the errors, as those obtained with the baseline model. From our best-fitting model, we infer that the ionized absorber has a column density of  cm−2 with ionization parameter
cm−2 with ionization parameter  , and that the gas is outflowing from the system at high velocity, namely, vout = 17000 ± 4500 km s−1. The NuSTAR 1 spectrum and best-fitting model are shown in the right panel of Figure 15. We note that the wind parameters that we derive from the NuSTAR 1 data are all consistent within the errors with those reported by other authors who made use of a simultaneous Chandra observation as well (Feruglio et al. 2015). This is reassuring in terms of the reality of the wind detection in the NuSTAR 1 observation.
, and that the gas is outflowing from the system at high velocity, namely, vout = 17000 ± 4500 km s−1. The NuSTAR 1 spectrum and best-fitting model are shown in the right panel of Figure 15. We note that the wind parameters that we derive from the NuSTAR 1 data are all consistent within the errors with those reported by other authors who made use of a simultaneous Chandra observation as well (Feruglio et al. 2015). This is reassuring in terms of the reality of the wind detection in the NuSTAR 1 observation.
We then perform fits including a putative ionized outflow similar to all other NuSTAR observations, but we do not find any statistical evidence for the presence of such component in any of the high-radio state NuSTAR observations (NuSTAR 2–5). This is true also for the NuSTAR 4 observation despite the fact that its spectral shape appears to be the most similar to NuSTAR 1 (see Figure 14), and we only obtain an improvement of  for 3 dof for the NuSTAR 4 observation when a wind model is included. Obviously, this does not mean that the wind is absent during the NuSTAR 2–5 observations, but only that its presence is not required by the data (using our specific wind model). The only significant detection is thus obtained during the only low-radio-flux state observation NuSTAR 1, where it explains well the observed deficit of soft X-ray photons below 12 keV. If the flux deficit during the radio-weak state is indeed due to an X-ray-absorbing wind then this is perhaps suggestive of a phenomenon known to occur in Galactic black hole accreting systems, where jet production is seen to suppress winds of X-ray-absorbing gas (Neilsen & Lee 2009). It would also provide an interesting analogy to the suppression of BAL winds in radio-loud states noted for Mrk 231 in the last section.
for 3 dof for the NuSTAR 4 observation when a wind model is included. Obviously, this does not mean that the wind is absent during the NuSTAR 2–5 observations, but only that its presence is not required by the data (using our specific wind model). The only significant detection is thus obtained during the only low-radio-flux state observation NuSTAR 1, where it explains well the observed deficit of soft X-ray photons below 12 keV. If the flux deficit during the radio-weak state is indeed due to an X-ray-absorbing wind then this is perhaps suggestive of a phenomenon known to occur in Galactic black hole accreting systems, where jet production is seen to suppress winds of X-ray-absorbing gas (Neilsen & Lee 2009). It would also provide an interesting analogy to the suppression of BAL winds in radio-loud states noted for Mrk 231 in the last section.
5.2. The 2015 XMM-Newton Observations
Mrk 231 has been observed three times with XMM-Newton, twice in this observing program and once in 2001. As can be seen from the light curve in Figure 1, the radio state is unknown during the 2001 XMM-Newton observation (Braito et al. 2004). So we have two observations during active jet states and one during an unknown epoch of jet activity. Figure 16 shows that there is no measurable difference between the three spectra obtained with XMM-Newton.
Figure 16. EPIC-pn spectrum from the three epochs of XMM-Newton observations showing no significant spectral/flux variability.
Download figure:
Standard image High-resolution imageEven though the 2015 XMM-Newton spectra are redundant with the 2001 spectrum, we proceed with a simple spectral analysis of these data. XMM-Newton and NuSTAR observed Mrk 231 simultaneously on 2015 May 28. We then start our analysis with this data set, performing simultaneous fits to the low- and high-energy data from the two missions, to gain insights into the overall broadband spectrum of Mrk 231. A constant is introduced to account for any cross-calibration issue between the two missions. The XMM-Newton EPIC-pn data (XMM 3) are considered in the 0.5–12 keV band, while the NuSTAR 5 data (A+B detectors) are used in the 3–30 keV band as above. The soft X-ray emission below ∼2 keV is dominated by extended emission (star formation, photoionized gas, etc.), and it can be successfully modeled by means of a two-temperature thermal plasma model plus a power-law component representing scattered emission. These two components are thought to originate far away from the central engine, and are thus only absorbed by the Galactic column. As for the  spectrum, several models are possible (see, e.g., Piconcelli et al. 2013), and we start here from the simplest possible one, namely, an extra absorption component at the redshift of Mrk 231 acting on a power-law continuum plus Fe line (i.e., the same baseline model that was applied to the NuSTAR data in the previous subsection).
spectrum, several models are possible (see, e.g., Piconcelli et al. 2013), and we start here from the simplest possible one, namely, an extra absorption component at the redshift of Mrk 231 acting on a power-law continuum plus Fe line (i.e., the same baseline model that was applied to the NuSTAR data in the previous subsection).
This first attempt provides a good statistical result with  for 134 dof. The temperature of the hot plasmas is
for 134 dof. The temperature of the hot plasmas is  and
and  , and this component contributes to the soft 0.5–2 keV band with a total luminosity of
, and this component contributes to the soft 0.5–2 keV band with a total luminosity of  erg
erg  . The soft (scattered) power law has a loosely constrained photon index
. The soft (scattered) power law has a loosely constrained photon index  and contributes to the 0.5–2 keV luminosity with an additional
and contributes to the 0.5–2 keV luminosity with an additional  erg
erg  . As for the high-energy emission, the X-ray nuclear continuum is well described by a power law with
. As for the high-energy emission, the X-ray nuclear continuum is well described by a power law with  with an intrinsic 2–10 keV (10–30 keV) luminosity of
with an intrinsic 2–10 keV (10–30 keV) luminosity of  erg
erg  (
( erg
erg  ). If the spectral model is extrapolated down to 0.5 keV, the total 0.5–30 keV intrinsic luminosity of the AGN turns out to be
). If the spectral model is extrapolated down to 0.5 keV, the total 0.5–30 keV intrinsic luminosity of the AGN turns out to be  erg
erg  . However, as the intrinsic continuum is in fact detected only above a few keV due to intervening absorption, we caution that this value should be treated with caution as we ignore the true AGN spectrum in the 0.5–2 keV band (where standard AGNs often exhibit a soft X-ray excess). The neutral absorber has a column density of
. However, as the intrinsic continuum is in fact detected only above a few keV due to intervening absorption, we caution that this value should be treated with caution as we ignore the true AGN spectrum in the 0.5–2 keV band (where standard AGNs often exhibit a soft X-ray excess). The neutral absorber has a column density of  cm−2, consistent with that derived from the NuSTAR 5 data alone (
cm−2, consistent with that derived from the NuSTAR 5 data alone ( cm−2). We detect an Fe emission line at 6.6 ± 0.1 keV with EW ∼ 180 eV. An emission feature appears to be present around 5.7 keV in the XMM 3 and, with less contrast, NuSTAR 5 spectra. The addition of a further emission line with σ fixed at 10 eV results in a statistically significant improvement of
cm−2). We detect an Fe emission line at 6.6 ± 0.1 keV with EW ∼ 180 eV. An emission feature appears to be present around 5.7 keV in the XMM 3 and, with less contrast, NuSTAR 5 spectra. The addition of a further emission line with σ fixed at 10 eV results in a statistically significant improvement of  for 2 dof for a line energy of 5.7 ± 0.1 keV and an equivalent width of ∼190 eV. No significant absorption feature that may indicate the presence of an ionized wind is seen in the XMM 3 data, as already noted in the analysis of the NuSTAR 5 data alone.
for 2 dof for a line energy of 5.7 ± 0.1 keV and an equivalent width of ∼190 eV. No significant absorption feature that may indicate the presence of an ionized wind is seen in the XMM 3 data, as already noted in the analysis of the NuSTAR 5 data alone.
The previous XMM 2 observation that took place on 2015 April 25 can be described by a very similar model. The only noticeable difference is that the Fe band appears to be simpler than on May 28. A simple Fe emission line at 6.7 ± 0.1 keV with equivalent width of ∼200 eV describes well all the emission, casting some doubts on the reality of the 5.7 keV emission line detected on May 28. The intrinsic continuum photon index is very loosely constrained by the XMM-Newton data alone ( ), and it is absorbed by a column density of
), and it is absorbed by a column density of  cm−2. The resulting best-fitting statistics is
cm−2. The resulting best-fitting statistics is  for 87 dof, and no features indicate the presence of a further ionized absorber during the XMM 2 observation.
for 87 dof, and no features indicate the presence of a further ionized absorber during the XMM 2 observation.
5.3. Summary of the X-Ray–radio Connection
The X-ray spectrum of Mrk 231 has been very constant over all epochs. Because of X-ray absorption of the nuclear emission, the very soft X-ray emission below a few keV is dominated by extended components (star-forming regions, scattering, re-emission by photoionized gas, etc.) and the stability of the X-ray emission is expected. On the other hand, the remarkably constant X-ray flux (and spectral shape) above 10 keV indicates that the intrinsic nuclear emission is not varying on timescales of years. It is curious how the far-UV and X-ray spectra tend to be very stable, quite unusual for a broadline AGN. The only epoch where an elevated flux density above 10 keV was seen was with Suzaku (Piconcelli et al. 2013), where it was explained as a transient uncovering of the X-ray nucleus (no radio sampling is available around the Suzaku epoch).
From a radio point of view, besides the XMM 1 observation that was performed during an unknown radio state, the NuSTAR 1 pointing is the only one that is performed during a low-radio flux state, while all others (NuSTAR 2–5 and XMM 2–3) are obtained during high radio-flux states. It is interesting to note that the NuSTAR 1 spectrum is precisely the only one that cannot be well described by the simple spectral model used for all other observations. The NuSTAR 1 spectrum presents a deficit of relatively soft X-ray photons (mostly in the 6.5–10 keV band), while it is indistinguishable from all others at higher energies, where the intrinsic nuclear emission dominates. This peculiar spectral shape is best explained by the addition of a further X-ray absorption component in the form of a fast ionized wind with outflow velocity vout ∼ 17,000 km s−1. Such a wind solution is not statistically required by the data in any of the high-radio state observations. The presence of an ultra-fast X-ray wind in 2012 August was previously claimed by others who made additional use of higher quality Chandra data, simultaneous with NuSTAR 1 (Feruglio et al. 2015). The wind parameters that we derive from the NuSTAR 1 data alone are in excellent agreement with those previously derived, which indicates that our detection and modeling are robust.
There being only one low-radio-state data point, we do not know if the presence of the wind is related to suppressed jet emission, but it is suggestive that our findings are in line with the phenomenology of Galactic black hole binaries where winds and jets seem to be mutually exclusive. If the X-ray wind was indeed present (or stronger) only during periods of suppressed jet activity, it would also link well with the suppression of BAL winds during high radio-flux states, as noted in the previous section.
6. Conclusion
In this article we used our long-term radio monitoring at high frequency and a ToO monitoring of a strong radio flare with VLBA, XMM-Newton, and NuSTAR in order to probe the radio-jet–accretion-disk connection in Mrk 231.
6.1. Results
In spite of some information loss due to poor beam shape in two of our epochs, we were able to determine a few interesting constraints on the jet–disk connection in this quasar.
- 1.
- 2.In Section 3.2, we were able to constrain the apparent speed of one of these ejections to
 .
. - 3.
- 4.
- 5.
- 6.
6.2. Physical Interpretation of Results
The primary result of this VLBI observation program was the detection of ejected components and estimating the apparent velocity,  . This allows us to attain new kinematic insight into the jet. Previously, using the methods of Ghosh & Punsly (2007), the time-variability brightness temperature is
. This allows us to attain new kinematic insight into the jet. Previously, using the methods of Ghosh & Punsly (2007), the time-variability brightness temperature is  K (Reynolds et al. 2009). In order to avoid the inverse Compton catastrophe, the analysis in Ghosh & Punsly (2007) indicates that the line of sight to the jet is less than
K (Reynolds et al. 2009). In order to avoid the inverse Compton catastrophe, the analysis in Ghosh & Punsly (2007) indicates that the line of sight to the jet is less than  . This equates to a time-variability factor
. This equates to a time-variability factor  for an optically thick, unresolved core (Ghosh & Punsly 2007). The Doppler factor, δ, is given in terms of Γ, the Lorentz factor of the outflow; β, the three velocity of the outflow and the angle of propagation to the line of sight, θ; and
for an optically thick, unresolved core (Ghosh & Punsly 2007). The Doppler factor, δ, is given in terms of Γ, the Lorentz factor of the outflow; β, the three velocity of the outflow and the angle of propagation to the line of sight, θ; and ![$\delta =1/[{\rm{\Gamma }}(1-\beta \cos \theta )]$](https://content.cld.iop.org/journals/0004-637X/836/2/155/revision1/apjaa5637ieqn127.gif) (Lind & Blandford 1985). Figure 17 combines our previous findings with the new estimate of the component apparent velocity,
(Lind & Blandford 1985). Figure 17 combines our previous findings with the new estimate of the component apparent velocity,  . The figure plots
. The figure plots  as a function of δ. The theoretical plots are made for various lines of sight (LOS) that are allowed kinematically. We now have two constraints on δ and
as a function of δ. The theoretical plots are made for various lines of sight (LOS) that are allowed kinematically. We now have two constraints on δ and  if we assume a steady jet structure over time. The intersection of the two lower bounds is shaded in gray. The arrows indicate the direction of increasing Γ on each curve. It is interesting that the new constraint does not significantly improve the previous limit on the LOS,
if we assume a steady jet structure over time. The intersection of the two lower bounds is shaded in gray. The arrows indicate the direction of increasing Γ on each curve. It is interesting that the new constraint does not significantly improve the previous limit on the LOS,  . The estimate of
. The estimate of  essentially indicates consistency with the time variability Doppler factor analysis. Combining the two conditions in Figure 17 indicates that
essentially indicates consistency with the time variability Doppler factor analysis. Combining the two conditions in Figure 17 indicates that  which is a new constraint on the jet kinematics. This highly relativistic motion is consistent with the point of jet origin deep within the gravitational potential well, possibly the innermost regions of the accretion disk.
which is a new constraint on the jet kinematics. This highly relativistic motion is consistent with the point of jet origin deep within the gravitational potential well, possibly the innermost regions of the accretion disk.
Figure 17. Apparent velocity vs. Doppler factor for various LOS. The shaded gray area is consistent with the lower bounds on the time variability Doppler factor from Reynolds et al. (2009) and  from this paper. The arrows indicate the direction of increasing Γ along each curve.
from this paper. The arrows indicate the direction of increasing Γ along each curve.
Download figure:
Standard image High-resolution imageIn principle, polarimetry can provide useful diagnostics of jet activity. Unfortunately, in Reynolds et al. (2009), it was found that there was no detectable polarized flux in our VLBA observations. Presumably, the emission is depolarized by a large scattering column density during the radiative transfer through the enveloping dense nuclear environment. Consequently, the 2015 observations were not a polarization experiment, so there was no polarization calibrator in order to maximize the amount of time on the source. Even so, we looked for evidence of polarization and could not find any.
Since the relativistic jet has a plausible origin in the inner accretion disk, there is a straightforward interpretation of point 4, above. A deficit of far-UV emission in active jet states suggests a connection to the "EUV deficit" of radio-loud quasars: radio-loud quasars show a tendency to have a deficit of extreme ultraviolet (EUV) flux shortward of the peak of the SED around  relative to the EUV flux levels found in RQQs (Zheng et al. 1997; Telfer et al. 2002; Punsly 2014, 2015; Punsly et al. 2016). The magnitude of the deficit increases with the strength of the jet (Punsly 2015). The analogy is not direct because the SED of Mrk 231 is extremely unusual and not well understood, especially in the UV (Veilleux et al. 2013, 2016). The continuum is likely observed through multiple "exotic" absorbing media that differ from the Galactic interstellar medium (Reynolds et al. 2013a; Veilleux et al. 2013). The far-UV flux is highly depressed in overall magnitude, yet the SED is very flat from 1400 to 2000 Å, not typical of absorption by a dusty interstellar medium (see Figure 12). However, we can draw one commonality with the EUV deficit of radio-loud quasars, the flux is lower at wavelengths shortward of the far-UV peak of the SED when there is an active jet as compared to the flux level when the jet is in a quiescent state. It might be that the disk in Mrk 231 is very cool as a consequence of energy losses due to winds driven by the continuum that is emitted from the inner disk (Laor & Davis 2014). Regardless of the reason for the low frequency of the SED turnover, the highest frequency optically thick thermal emission should represent emission from the innermost accretion disk. This emission should be detected near or just blueward of the far-UV break in the SED (Sun & Malkan 1989; Szuszkiewicz et al. 1996). Figure 12 seems to indicate that the optically thick thermal emission from the innermost accretion disk (i.e., emission just shortward of the peak of the SED) is lower when there is a radio jet similar to the "EUV deficit" in radio-loud quasars. In particular, the "EUV deficit in radio loud quasars" has been shown to be consistent with the predicted trends of a simple magnetically arrested accretion scenario in which islands of large-scale vertical magnetic flux thread the innermost accretion flow in radio-loud quasars. This distribution of flux is located at the base of the relativistic jet and at the same time displaces the optically thick gas responsible for the thermal emission from the innermost accretion disk, thereby reducing the flux beyond the peak of the SED relative to that of RQQs (Punsly 2014, 2015). Applying this dynamic to Mrk 231, the displaced far-UV emitting gas equates to a diminished far-UV luminosity, and the increased vertical flux creates a stronger jet. This creates an inverse correlation between the far-UV luminosity and jet power.
relative to the EUV flux levels found in RQQs (Zheng et al. 1997; Telfer et al. 2002; Punsly 2014, 2015; Punsly et al. 2016). The magnitude of the deficit increases with the strength of the jet (Punsly 2015). The analogy is not direct because the SED of Mrk 231 is extremely unusual and not well understood, especially in the UV (Veilleux et al. 2013, 2016). The continuum is likely observed through multiple "exotic" absorbing media that differ from the Galactic interstellar medium (Reynolds et al. 2013a; Veilleux et al. 2013). The far-UV flux is highly depressed in overall magnitude, yet the SED is very flat from 1400 to 2000 Å, not typical of absorption by a dusty interstellar medium (see Figure 12). However, we can draw one commonality with the EUV deficit of radio-loud quasars, the flux is lower at wavelengths shortward of the far-UV peak of the SED when there is an active jet as compared to the flux level when the jet is in a quiescent state. It might be that the disk in Mrk 231 is very cool as a consequence of energy losses due to winds driven by the continuum that is emitted from the inner disk (Laor & Davis 2014). Regardless of the reason for the low frequency of the SED turnover, the highest frequency optically thick thermal emission should represent emission from the innermost accretion disk. This emission should be detected near or just blueward of the far-UV break in the SED (Sun & Malkan 1989; Szuszkiewicz et al. 1996). Figure 12 seems to indicate that the optically thick thermal emission from the innermost accretion disk (i.e., emission just shortward of the peak of the SED) is lower when there is a radio jet similar to the "EUV deficit" in radio-loud quasars. In particular, the "EUV deficit in radio loud quasars" has been shown to be consistent with the predicted trends of a simple magnetically arrested accretion scenario in which islands of large-scale vertical magnetic flux thread the innermost accretion flow in radio-loud quasars. This distribution of flux is located at the base of the relativistic jet and at the same time displaces the optically thick gas responsible for the thermal emission from the innermost accretion disk, thereby reducing the flux beyond the peak of the SED relative to that of RQQs (Punsly 2014, 2015). Applying this dynamic to Mrk 231, the displaced far-UV emitting gas equates to a diminished far-UV luminosity, and the increased vertical flux creates a stronger jet. This creates an inverse correlation between the far-UV luminosity and jet power.
The other possibly very interesting finding is point 5, above. Recall that the existence of large-scale jets and BAL winds are almost mutually exclusive. The propensity for suppressed large-scale emission increases strongly with the BALnicity index (Becker et al. 2000, 2001). Figure 12 and Table 2 indicate that Mrk 231 might be a unique source in which we can see the relativistic jet and high-ionization BAL wind anti-correlation occurring in real time. This wind suppression is naturally explained by models in which the BAL wind is launched from the innermost regions of the accretion flow, including the outer boundary of the central accretion vortex (Punsly 1999a, 1999b). In these models, the propensity of a quasar accretion flow to launch either a BAL wind or a radio jet is determined by the ratio of radiation pressure to magnetic pressure of the large-scale magnetic field in the central vortex and the inner edge of the accretion disk. Thus, points 4 and 5 are consistent if the jet and BAL wind are both launched from the inner accretion disk and accretion vortex. In Mrk 231, the ratio of the magnetic pressure from magnetic islands to the thermal radiation pressure from optically thick gas vacillates. Sometimes the magnetic islands are plentiful and a modest relativistic jet is launched (suppressing the BAL wind and far-UV) and at other times the magnetic islands have diffused away and the spectrum of Mrk 231 hardens in the far-UV and a high-ionization wind is launched.
One might wonder how the increased X-ray flux during the state of high jet activity in point 6 is consistent with these other two findings. The most direct interpretation is that the X-ray excess in the high-radio state is a consequence of inverse Compton emission from the same electrons that produce the synchrotron emission in the jet. The spectral index would be slightly steeper than that of the X-ray power law of the coronal X-rays. Considering the superluminal speed in point 2, above, one would expect significant Doppler enhancement of a very weak X-ray source, and the resultant flux is likely highly variable. The other possibility is that the reduced X-ray flux in the low-radio states is a result of an X-ray-absorbing wind (Feruglio et al. 2015). When the jet is active, the dynamics of this X-ray wind launching mechanism (X-ray radiation pressure from the corona) is disrupted by the magnetic islands. The data are not sufficient to distinguish between the two possibilities. However, we show in Section 5 that the difference in the NuSTAR spectrum during the low-radio state compared to the high-radio states is well described by the presence of absorption in a photoionized wind. This is the more intriguing of the two possibilities since it suggests that the existence of a strong jet suppresses both the UV-absorbing and the X-ray-absorbing winds. The latter is a phenomenon known to occur in Galactic black hole accreting systems, where jet production is seen to suppress X-ray winds (Neilsen & Lee 2009). This could be the first evidence of a direct analogy between the jet–wind connection in supermassive black holes and stellar mass black holes.
6.3. Future Observations
Based on these three important inferences of our study, it seems that obtaining one or two HST COS G140L observations in a state of low jet activity would verify if there is a trend for far-UV suppression and if the C iv broad absorption trough returns. Also, based on Figure 14, it would be interesting to monitor Mrk 231 in a weak jet state in order to see if the X-ray emission decreases. A combined NuSTAR and XMM-Newton (or Chandra) observation could verify if the X-ray-driven wind that was claimed in this low state in Feruglio et al. (2015) returns. Furthermore, longer X-ray observations are required to constrain the X-ray-driven wind in both the high- and low-radio sates. If VLBA observations are obtained during another radio flare, it is important to stress the requirement that the u–v coverage not be compromised by splitting the observation for scheduling purposes. If the observations are split, care must be taken to ensure that two unique LST ranges are obtained on the two consecutive days. It is far better to delay the observation a week or two than compromise the u–v coverage. With this constraint, a multi-epoch campaign should see an ejected component evolve in space and time. An HST COS G140L observation in the the rising high-flare state has not been obtained, and it would be of interest to see if the spectrum is the same as other times during the jet formation.
This research made use of data obtained with NuSTAR, a project led by Caltech, funded by NASA and managed by NASA/JPL, and utilized the NUSTARDAS software package, jointly developed by the ASDC (Italy) and Caltech (USA). We also made use of data obtained with XMM-Newton, an ESA science mission with instruments and contributions directly funded by ESA Member States. This work made use of Director's Discretionary Time on both NuSTAR and XMM-Newton for which we thank Fiona Harrison and Norbert Schartel for approving, as well as the NuSTAR and XMM-Newton SOC for implementing and coordinating the observations. We would like to thank S. Veilleux and M. Melendez for sharing their G130M data. The National Radio Astronomy Observatory is a facility of the National Science Foundation operated under cooperative agreement by Associated Universities, Inc. This research has made use of NASA's Astrophysics Data System Bibliographic Services. This work made use of the Swinburne University of Technology software correlator, developed as part of the Australian Major National Research Facilities Programme and operated under licence.
Footnotes
- 8
The Arcminute Microkelvin Imager consists of two radio interferometric arrays located in the Mullard Radio Astronomical Observatory, Cambridge, UK (Zwart et al. 2008). Observations occur between 13.9 and 18.2 GHz in six frequency channels. The Small Array (AMI-SA) consists of ten 3.6 m diameter dishes with a maximum baseline of 20 m, with an angular resolution of 3', while the Large Array (AMI-LA) comprises eight 12.6 m diameter dishes with a maximum baseline of 110 m, giving an angular resolution of 0
 5.
5.































