Abstract
The structure of the steady axisymmetric force-free magnetosphere of a Kerr black hole (BH) is governed by a second-order partial differential equation of Aϕ depending on two "free" functions 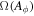 and
and 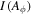 , where Aϕ is the ϕ component of the vector potential of the electromagnetic field, Ω is the angular velocity of the magnetic field lines, and I is the poloidal electric current. In this paper, we investigate the solution uniqueness. Taking the asymptotically uniform field as an example, analytic studies imply that there are infinitely many solutions approaching the uniform field at infinity, while only a unique one is found in general relativistic magnetohydrodynamic simulations. To settle the disagreement, we reinvestigate the structure of the governing equation and numerically solve it with given constraint and boundary conditions. We find that the constraint condition (field lines smoothly crossing the light surface) and boundary conditions at the horizon and at infinity are connected via radiation conditions at horizon and at infinity, rather than being independent. With appropriate constraint and boundary conditions, we numerically solve the governing equation and find a unique solution. Contrary to naive expectations, our numerical solution yields a discontinuity in the angular velocity of the field lines and a current sheet along the last field line crossing the event horizon. We also briefly discuss the applicability of the perturbation approach to solving the governing equation.
, where Aϕ is the ϕ component of the vector potential of the electromagnetic field, Ω is the angular velocity of the magnetic field lines, and I is the poloidal electric current. In this paper, we investigate the solution uniqueness. Taking the asymptotically uniform field as an example, analytic studies imply that there are infinitely many solutions approaching the uniform field at infinity, while only a unique one is found in general relativistic magnetohydrodynamic simulations. To settle the disagreement, we reinvestigate the structure of the governing equation and numerically solve it with given constraint and boundary conditions. We find that the constraint condition (field lines smoothly crossing the light surface) and boundary conditions at the horizon and at infinity are connected via radiation conditions at horizon and at infinity, rather than being independent. With appropriate constraint and boundary conditions, we numerically solve the governing equation and find a unique solution. Contrary to naive expectations, our numerical solution yields a discontinuity in the angular velocity of the field lines and a current sheet along the last field line crossing the event horizon. We also briefly discuss the applicability of the perturbation approach to solving the governing equation.
Export citation and abstract BibTeX RIS
1. Introduction
The Blandford–Znajek (BZ) mechanism (Blandford & Znajek 1977) is believed to be one of most efficient ways to extract rotation energy from spinning black holes (BHs), which operates in BH systems on all mass scales, from the stellar-mass BHs of gamma-ray bursts to the supermassive BHs of active galactic nuclei. In the past decade, we have gained a better understanding of the BZ mechanism from general relativistic magnetohydrodynamic (GRMHD) simulations (e.g., Komissarov 2001, 2004a, 2004b, 2005; McKinney & Gammie 2004; Semenov et al. 2004; McKinney 2005; Komissarov & McKinney 2007; McKinney & Narayan 2007a, 2007b; Tchekhovskoy et al. 2008, 2010, 2011; Nagataki 2009, 2011; Palenzuela et al. 2011; Alic et al. 2012; Tchekhovskoy & McKinney 2012; McKinney et al. 2013; Penna et al. 2013), numerical solutions (e.g., Fendt 1997; Uzdensky 2004, 2005; Palenzuela et al. 2010; Contopoulos et al. 2013; Nathanail & Contopoulos 2014), and analytic perturbation solutions (e.g., Tanabe & Nagataki 2008; Beskin & Zheltoukhov 2013; Gralla & Jacobson 2014; Pan & Yu 2014, 2015a, 2015b, 2016; Gralla et al. 2015, 2016b; Penna 2015; Yang et al. 2015) to the steady axisymmetric force-free electrodynamics in the Kerr spacetime.5
Various studies converge to a common picture of how the BZ mechanism operates: the spinning BH distorts the poloidal magnetic field  and induces the poloidal electric field
and induces the poloidal electric field  and toroidal magnetic field
and toroidal magnetic field  , which generate an outward Poynting flux
, which generate an outward Poynting flux  along the magnetic field lines threading the spinning BH. The rotation energy of the spinning BHs is extracted in the form of Poynting flux (Komissarov 2009; Beskin 2010).
along the magnetic field lines threading the spinning BH. The rotation energy of the spinning BHs is extracted in the form of Poynting flux (Komissarov 2009; Beskin 2010).
Going a step further, it is natural to ask whether these different approaches give qualitatively and quantitatively consistent descriptions of the BH magnetosphere structure, e.g., the topology of magnetic fields, the electric current distributions, the angular velocities of the magnetic field lines, and the energy extraction rates. The answer is yes and no. The axisymmetric, steady-state, force-free magnetosphere around Kerr BHs is governed by the general relativistic Grad–Shafranov (GS) equation. For the simplest magnetic field configuration, split monopole field, both analytic (Pan & Yu 2015a) and numerical solutions (Nathanail & Contopoulos 2014) reproduce the simulated angular velocity of field lines Ω, poloidal electric current I, and energy extraction rate  to high precision (Tchekhovskoy et al. 2010). But for the asymptotically uniform field, different approaches do not even reach a consensus on the solution uniqueness. Time-dependent simulations (e.g., Komissarov 2005; Komissarov & McKinney 2007; Yang et al. 2015) seem to converge to a unique solution. Previous analytic studies (Beskin & Zheltoukhov 2013; Pan & Yu 2014; Gralla et al. 2016b) seem to find a unique perturbation solution that roughly agrees with GRMHD simulations. But in this paper, we will show that there are actually many of them, due to the superposition of the monopole component (and other possible components). According to the argument of Nathanail & Contopoulos (2014), solving the GS equation is actually an eigenvalue problem, with two eigenvalues
to high precision (Tchekhovskoy et al. 2010). But for the asymptotically uniform field, different approaches do not even reach a consensus on the solution uniqueness. Time-dependent simulations (e.g., Komissarov 2005; Komissarov & McKinney 2007; Yang et al. 2015) seem to converge to a unique solution. Previous analytic studies (Beskin & Zheltoukhov 2013; Pan & Yu 2014; Gralla et al. 2016b) seem to find a unique perturbation solution that roughly agrees with GRMHD simulations. But in this paper, we will show that there are actually many of them, due to the superposition of the monopole component (and other possible components). According to the argument of Nathanail & Contopoulos (2014), solving the GS equation is actually an eigenvalue problem, with two eigenvalues  and
and  to be determined by requiring field lines to smoothly cross the light surfaces (LSs). For common field configurations, there usually exist two LSs, sufficing to determine two eigenvalues. With only one LS for the uniform field configuration and one more boundary condition, Nathanail & Contopoulos (2014) numerically found a unique solution, which, however, shows distinctive features from previous GRMHD simulations (Komissarov 2005).
to be determined by requiring field lines to smoothly cross the light surfaces (LSs). For common field configurations, there usually exist two LSs, sufficing to determine two eigenvalues. With only one LS for the uniform field configuration and one more boundary condition, Nathanail & Contopoulos (2014) numerically found a unique solution, which, however, shows distinctive features from previous GRMHD simulations (Komissarov 2005).
How can the relationship between the unique solution and the infinitely many possible candidates, and the discrepancy between previous numerical solutions and GRMHD simulations, be explained?6 Does the plasma inertia make a difference? The force-free condition is assumed in both analytic and numerical solutions, but the inertia cannot be completely ignored in simulations. Taking account of the plasma inertia, Takahashi et al. (1990) proposed the so-called MHD Penrose process, where the plasma particles within the ergosphere are projected onto negative-energy orbits by magnetic field and eventually are captured by the central BH. As a result, Alfvèn waves are generated along the magnetic field lines, and BH rotation energy is carried away by these Alfvèn waves. Koide et al. (2002) and Koide (2003) found that the MHD Penrose process was operating in GRMHD simulations (see e.g., Koide & Baba 2014; Lasota et al. 2014; Toma & Takahara 2014, 2016; Kojima 2015, for recent discussions on this issue). If the MHD Penrose process is the dominant energy extraction process, the unique solution found in simulations actually describes the MHD Penrose process instead of the BZ mechanism. However, later simulations showed that the MHD Penrose process is only a transient state, after which the Alfvèn waves decay, the system settles down into a steady state, and the BZ mechanism takes over (e.g., Komissarov 2005). Therefore, the plasma inertia seems to make little difference after the system settles down into the steady state.
Another possible explanation is that, among all these mathematically possible solutions, only the one found in simulations is stable. Yang & Zhang (2014) and Yang et al. (2015) analyzed the stability of these solutions, and no unstable mode was found at order O(a), where a is the dimensionless BH spin. Therefore, modes can be unstable with a growth rate at  at most.7
But the relevant timescale is much longer than the transient timescales observed in simulations. Therefore, they concluded that the selection rule unlikely comes from instability.
at most.7
But the relevant timescale is much longer than the transient timescales observed in simulations. Therefore, they concluded that the selection rule unlikely comes from instability.
In this paper, we show that the uniform field solution is unique, as strongly implied by previous GRMHD simulations and pointed out by Nathanail & Contopoulos (2014). Following the algorithm proposed by Contopoulos et al. (2013) and Nathanail & Contopoulos (2014), we numerically find a unique combination of Ω and I, ensuring both smooth field lines across the LS and a uniform field at infinity. Contrary to Nathanail & Contopoulos (2014), our numerical solution yields a discontinuity in the angular velocity of field lines and a current sheet along the last field line crossing the event horizon, which are features found in previous simulations.
We also investigate the applicability of the analytic perturbation approach to the GS equation, which relies on a fixed unperturbed solution and the priorly known asymptotic behavior of the magnetic field. The analytic approach breaks down if either of the two factors is violated. Both of them are satisfied for the monopole field in Kerr spacetime; therefore, we see the perfect match between high-order perturbation solutions and results from simulations and numerical solutions. But for the uniform field, the unperturbed background field is not fixed, due to the superposition of the monopole component; therefore, the perturbation approach cannot predict a unique solution.
The paper is organized as follows. In Section 2, we summarize the basic equations governing the steady axisymmetric force-free magnetospheres. In Section 3, we clarify the relation between constraint conditions, radiation conditions, and boundary conditions, as well as our numerical method to solve the GS equation. We apply the perturbation approach on the uniform field problem and clarify the applicability of the analytic perturbation approach in Section 4. Summary and discussions are given in Section 5. In the
2. Basic Equations
In the force-free approximation, electromagnetic energy greatly exceeds that of matter. Consequently, the force-free magnetosphere is governed by the energy conservation equation of the electromagnetic field, conventionally called the GS equation. In the Kerr spacetime, the axisymmetric and steady GS equation is written as (Pan & Yu 2014)

which expands as (see also, e.g., Contopoulos et al. 2013; Nathanail & Contopoulos 2014; Pan & Yu 2016, in slightly different forms)

where  ,
,  ,
,  ,
,  , and the primes designate derivatives with respect to Aϕ. For clarity, we may write the GS equation in a more illustrating form.
, and the primes designate derivatives with respect to Aϕ. For clarity, we may write the GS equation in a more illustrating form.

where  is the prefactor of
is the prefactor of  in Equation (2),
in Equation (2),  denotes the partial derivative with respect to coordinate i with Ω fixed, and
denotes the partial derivative with respect to coordinate i with Ω fixed, and  is the derivative with respect to Ω. The GS equation written in this compact form manifests clear symmetry and therefore is beneficial in various aspects.8
is the derivative with respect to Ω. The GS equation written in this compact form manifests clear symmetry and therefore is beneficial in various aspects.8
3. The Solution Uniqueness Problem
In this section, we first clarify all the constraint conditions the GS equation satisfies, as well as their relation with boundary conditions at the horizon and at infinity. We find that the constraint conditions and boundary conditions are not independent. For a given  , we can numerically find an
, we can numerically find an  ensuring field lines smoothly crossing the LS, but the combination of
ensuring field lines smoothly crossing the LS, but the combination of  and
and  obtained this way usually is in conflict with the uniform field boundary condition at infinity. To be consistent with this boundary condition,
obtained this way usually is in conflict with the uniform field boundary condition at infinity. To be consistent with this boundary condition,  and
and  must satisfy one more constraint. Then, we numerically find the unique combination of
must satisfy one more constraint. Then, we numerically find the unique combination of  and
and  that ensures that field lines smoothly cross the LS and is consistent with the boundary condition at infinity. Finally, we compare our numerical solution with previous studies.
that ensures that field lines smoothly cross the LS and is consistent with the boundary condition at infinity. Finally, we compare our numerical solution with previous studies.
3.1. Constraint Conditions and Boundary Conditions
We want physically allowed solutions to be finite and smooth everywhere. At LS where  , the second-order GS equation degrades to a first-order equation
, the second-order GS equation degrades to a first-order equation

Field lines smoothly crossing the LS must satisfy the above constraint, which we call the LS crossing constraint condition. At the horizon and infinity, the requirement of solution finiteness leads to the radiation conditions (e.g., Pan & Yu 2016), which read as

and

where  is the angular velocity of the central BH.
is the angular velocity of the central BH.
But the radiation conditions and boundary conditions are not independent. For example, the radiation condition (5) uniquely determines the boundary values at the horizon if Ω and I are specified, and we will use it as the inner boundary condition in our numerical calculation. In the same way, the radiation condition (6) uniquely determines the boundary values at infinity, if Ω and I are specified; or the radiation condition (6) enforces a constraint on Ω and I, if the boundary condition at infinity is given. In our working example, the boundary condition at infinity

is given. Plugging it into the radiation condition (6), we find that Ω and I must satisfy a new constraint (Nathanail & Contopoulos 2014; Pan & Yu 2014, 2016),

Note that conditions (6), (7), and (8) are not independent, and we will use two of them, conditions (7) and (8), to close the GS equation.
Now we get two constraint conditions (4) and (8) and two boundary conditions in the r direction (5) and (7) ready, (where the inner boundary condition (5) is nontrivial; see the

where the horizon enclosed magnetic flux  is to be determined self-consistently.
is to be determined self-consistently.
Figure 1. Left: magnetic field lines around a Kerr BH with spin a = 0.99, where the inner (solid) curve and outer (dashed) curve are the ILS and IRS, respectively. Right: functions  and
and  of the uniform field configuration, where the latter is normalized by the amount of field flux crossing the event horizon
of the uniform field configuration, where the latter is normalized by the amount of field flux crossing the event horizon  .
.
Download figure:
Standard image High-resolution image3.2. Numerical Method and Results
The algorithm for numerically solving the GS equation was proposed by Contopoulos et al. (2013) and was optimized by Nathanail & Contopoulos (2014). We slightly tailor their algorithm to accommodate the problem we are working on. We define a new radial coordinate  , confine our computation domain
, confine our computation domain  in the region
in the region ![$[R({r}_{+}),1]\times [0,1]$](https://content.cld.iop.org/journals/0004-637X/836/2/193/revision1/apjaa5c36ieqn38.gif) , and implement a uniform 512 × 64 grid. The detailed numerical steps are as follows.
, and implement a uniform 512 × 64 grid. The detailed numerical steps are as follows.
1. We choose some initial guess Aϕ and trial functions Ω and I as follows:10

2. We evolve Aϕ using the relaxation method (Press et al. 1987), although this method does not work properly at the LS owing to the vanishing second-order derivatives. Fortunately, the directional derivative of Aϕ is known as a function of  there (see Equation (4)). We instead update Aϕ at the LS using neighborhood grid points and the directional derivative. From the directional derivative and the grid points on the left/right side, we obtain
there (see Equation (4)). We instead update Aϕ at the LS using neighborhood grid points and the directional derivative. From the directional derivative and the grid points on the left/right side, we obtain  /
/ . Usually the two are not equal and field lines are broken here. To smooth the field lines, we adjust
. Usually the two are not equal and field lines are broken here. To smooth the field lines, we adjust  and update
and update  as follows:
as follows:

where

Usually,  obtained is not very smooth. To avoid possible numerical instabilities, we fit
obtained is not very smooth. To avoid possible numerical instabilities, we fit  with eighth-order polynomials. In addition,
with eighth-order polynomials. In addition,  consists of two pieces: a regular piece determined as described above, and a singular piece (the current sheet part)
consists of two pieces: a regular piece determined as described above, and a singular piece (the current sheet part)

In our computation, we model the delta function as a parabola confined in a finite interval ![$[{A}_{\phi }^{{\rm{H}}},{A}_{\phi }^{{\rm{H}}}(1+\delta )]$](https://content.cld.iop.org/journals/0004-637X/836/2/193/revision1/apjaa5c36ieqn48.gif) with
with  (see e.g., Gruzinov 2005).
(see e.g., Gruzinov 2005).
3. Repeat step 2 10 times, and then update  according to the constraint (8).
according to the constraint (8).
We iterate the initial guess solution following the above steps until field lines smoothly cross the LS and satisfy the boundary conditions. The numerical results are shown in Figure 1. In the left panel, we show the convergent field configuration, which, as expected, matches those of simulations (e.g., Komissarov & McKinney 2007). In the right panel, we show functions  and
and  . From this plot, we see that the angular velocity of the last field line crossing the event horizon
. From this plot, we see that the angular velocity of the last field line crossing the event horizon  is not vanishing, i.e.,
is not vanishing, i.e.,  , while we expect the angular velocity of field lines not crossing the BH to vanish, i.e.,
, while we expect the angular velocity of field lines not crossing the BH to vanish, i.e.,  .
.
3.3. Comparison with Previous Studies
Nathanail & Contopoulos (2014) also studied the BH magnetosphere structure of the uniform field and concluded that both  and
and  must approach zero along the last field line crossing the event horizon, and therefore the ILS coincides with the IRS along the equator, and the electric current sheet does not appear. But as shown in the
must approach zero along the last field line crossing the event horizon, and therefore the ILS coincides with the IRS along the equator, and the electric current sheet does not appear. But as shown in the  at
at  , and therefore the ILS lies between the event horizon and the IRS, and there exists a current sheet. The discrepancies here can be settled by previous GRMHD simulations done by Komissarov (2005), where they observed a sharp transition in
, and therefore the ILS lies between the event horizon and the IRS, and there exists a current sheet. The discrepancies here can be settled by previous GRMHD simulations done by Komissarov (2005), where they observed a sharp transition in  at
at  and interpreted it as a discontinuity smeared by numerical viscosity. It is worth noting that the discontinuity in
and interpreted it as a discontinuity smeared by numerical viscosity. It is worth noting that the discontinuity in  does not lead to any physical difficulties, e.g., the continuity of
does not lead to any physical difficulties, e.g., the continuity of  across the LS is not affected.
across the LS is not affected.
In addition, we do not explicitly show the BZ power of the uniform field configuration here, because it is sensitive to the magnetic flux trapped by the event horizon  , which is boundary condition dependent. In the real astrophysical environment, it is mainly determined by the accretion process of the central BH (e.g., Garofalo 2009).
, which is boundary condition dependent. In the real astrophysical environment, it is mainly determined by the accretion process of the central BH (e.g., Garofalo 2009).
4. Applicability of Analytic Perturbation Approach
In this section, we first recap the analytic perturbation approach to the GS equation and then apply it to the uniform field problem (Pan & Yu 2014, 2015a) and explain why this approach actually yields many solutions. Finally, we discuss the applicability of the perturbation method.
We start with an unperturbed solution A0 in the Schwarzschild spacetime,

where the operator

For the corresponding Kerr metric solution  , we assume
, we assume  , define
, define  , and expand the solution to the leading order
, and expand the solution to the leading order

Then we linearize the GS Equation (2) as

by only keeping leading-order perturbation terms, where the source function S2 depends on i1 and  , which can be figured out from the radiation conditions at horizon and at infinity (5)–(6). The solution to the linearized GS equation is written as
, which can be figured out from the radiation conditions at horizon and at infinity (5)–(6). The solution to the linearized GS equation is written as

where  is the Green's function of operator
is the Green's function of operator  (Petterson 1974; Blandford & Znajek 1977),
(Petterson 1974; Blandford & Znajek 1977),

In this way, for a given Schwarzschild metric solution A0, the corresponding Kerr metric solution  is uniquely determined order by order. Applying the method on the uniform field problem
is uniquely determined order by order. Applying the method on the uniform field problem  , we find (Beskin & Zheltoukhov 2013; Pan & Yu 2014; Gralla et al. 2015)
, we find (Beskin & Zheltoukhov 2013; Pan & Yu 2014; Gralla et al. 2015)

where  is the magnetic flux trapped by the event horizon (
is the magnetic flux trapped by the event horizon ( for the lowest-order perturbation solution and generally depends on BH spins and boundary conditions).
for the lowest-order perturbation solution and generally depends on BH spins and boundary conditions).
It seems that we have found the unique solution (at leading order) approaching a uniform field at infinity, but this is not the case. The Schwarzschild spacetime GS Equation (14) is linear. Both the uniform field and monopole field are its solutions, so do their linear combinations are also its solutions,

where  is some constant coefficient. The mixture of the monopole component generates a family of Schwarzschild metric solutions,
is some constant coefficient. The mixture of the monopole component generates a family of Schwarzschild metric solutions,  , and all these solutions approach a uniform field at infinity. For each solution, the corresponding Kerr metric solution
, and all these solutions approach a uniform field at infinity. For each solution, the corresponding Kerr metric solution  can be obtained using the above perturbation method.
can be obtained using the above perturbation method.
To summarize, the perturbation method depends on two main ingredients: the known asymptotic field behavior at infinity  and the fixed underlying unperturbed field configuration A0. But for the uniform field problem, there are many mathematically allowed unperturbed solutions due to the additional monopole component. That's why the perturbation approach cannot predict the unique solution.
and the fixed underlying unperturbed field configuration A0. But for the uniform field problem, there are many mathematically allowed unperturbed solutions due to the additional monopole component. That's why the perturbation approach cannot predict the unique solution.
5. Summary and Discussions
The GS equation is a second-order differential equation with two to-be-determined functions Ω and I. Generally speaking, we need two constraint conditions to determine Ω and I, two boundary conditions in the r directions, and two boundary conditions in the μ direction to fix  . For an asymptotically uniform field, we use constraint conditions (4) and (8), boundary conditions in the r direction (5) and (7), and boundary conditions in the μ direction (9) to close the GS equation. Our numerical solution of the uniform field yields a discontinuity in the
. For an asymptotically uniform field, we use constraint conditions (4) and (8), boundary conditions in the r direction (5) and (7), and boundary conditions in the μ direction (9) to close the GS equation. Our numerical solution of the uniform field yields a discontinuity in the  at
at  ; therefore, the ILS lies between the event horizon and the IRS, and there exists a current sheet along the last field line crossing the event horizon (Figure 1), which is as expected from the horizon regularity condition.
; therefore, the ILS lies between the event horizon and the IRS, and there exists a current sheet along the last field line crossing the event horizon (Figure 1), which is as expected from the horizon regularity condition.
Following the same logic, let us reexamine two other well-studied field configurations: the monopole field in the Kerr spacetime and the dipole field in the flat spacetime (classical pulsars). For both field configurations, the number of LSs equals the number of to-be-determined functions I and Ω. For the monopole field in the Kerr spacetime, there are two LS crossing conditions and two radiation conditions. The former two determine Ω and I, and the latter two determine the inner and the outer boundaries. Hence, there is no more freedom for specifying a boundary condition at infinity, i.e., we actually do not know the solution at infinity before we really solve the GS equation. Previous simulations and numerical solutions indeed confirmed the asymptotic monopole field configuration  . For the pulsar dipole field, Ω is equal to the angular velocity of the central star and I is the only function to determine. The only LS uniquely determines I (Contopoulos et al. 1999), and two radiation conditions automatically determine boundary conditions. In the same way, there is no more freedom to impose a boundary condition at infinity. And previous numerical studies found that the field at infinity deviates from
. For the pulsar dipole field, Ω is equal to the angular velocity of the central star and I is the only function to determine. The only LS uniquely determines I (Contopoulos et al. 1999), and two radiation conditions automatically determine boundary conditions. In the same way, there is no more freedom to impose a boundary condition at infinity. And previous numerical studies found that the field at infinity deviates from  (e.g., Gralla et al. 2016a).
(e.g., Gralla et al. 2016a).
We also discuss the perturbation approach for solving the GS equation, whose applicability depends on two main ingredients: the known asymptotic field behavior at infinity  and the fixed underlying unperturbed field configuration A0. For the monopole field, both of them are satisfied; therefore, the perturbation approach is applicable and the high-order perturbation solutions show a good match with results from simulations (Pan & Yu 2015a). For both the uniform field in the Schwarzschild spacetime and the dipole field surrounding static stars, the superposition of the monopole component (and possible other components) generates many unperturbed solutions; as a result, the perturbation approach cannot predict a unique uniform field solution in the Kerr spacetime or a unique dipole field solution surrounding spinning stars.
and the fixed underlying unperturbed field configuration A0. For the monopole field, both of them are satisfied; therefore, the perturbation approach is applicable and the high-order perturbation solutions show a good match with results from simulations (Pan & Yu 2015a). For both the uniform field in the Schwarzschild spacetime and the dipole field surrounding static stars, the superposition of the monopole component (and possible other components) generates many unperturbed solutions; as a result, the perturbation approach cannot predict a unique uniform field solution in the Kerr spacetime or a unique dipole field solution surrounding spinning stars.
We thank our referee Prof. I. Contopoulos for his insightful comments on the validity of the radiation condition for vertical field configurations and on the possible difficulties arising from the discontinuity in the angular velocity of field lines. We also thank A. Nathanail for clearly explaining his numerical algorithm. C.Y. is grateful for the support by the National Natural Science Foundation of China (grants 11173057, 11373064, 11521303), the Yunnan Natural Science Foundation (grants 2012FB187 and 2014HB048), and the Youth Innovation Promotion Association, CAS. Part of the computation was performed at the HPC Center, Yunnan Observatories, CAS, China. L.H. acknowledges the support by the National Natural Science Foundation of China (grant 11203055). This paper is supported in part by the Strategic Priority Research Program "The Emergence of Cosmological Structures" of the Chinese Academy of Sciences, grant no. XDB09000000, and the Key Laboratory for Radio Astronomy, CAS. This work made extensive use of the NASA Astrophysics Data System and of the astro-ph preprint archive at arXiv.org.
Appendix
For a given combination of  and
and  , the horizon regularity condition (Equation (5)) uniquely determines the boundary condition at horizon
, the horizon regularity condition (Equation (5)) uniquely determines the boundary condition at horizon  . We find that its numerical solution is not trivial, due to the nonlinearity. To construct a robust solver, we first rewrite Equation (5) as
. We find that its numerical solution is not trivial, due to the nonlinearity. To construct a robust solver, we first rewrite Equation (5) as

where we have defined two normalized variables,  and
and  . Here
. Here  runs from 0 to 1, and its values on boundaries are
runs from 0 to 1, and its values on boundaries are  and
and  . Furthermore, we define
. Furthermore, we define  , and the above equation is written in a variable separated form
, and the above equation is written in a variable separated form

which has a formal solution

In this form, numerically solving  is stable.
is stable.
Here we show a general property of force-free magnetospheres read out of the formal solution (24): the horizon condition requires the existence of a current sheet at the equator. Enabling a nonsingular solution, the integral  must be finite, except at
must be finite, except at  , where
, where  owing to vanishing
owing to vanishing  . At
. At  , the finite integral requires nonzero
, the finite integral requires nonzero  , or quickly decreased
, or quickly decreased  (e.g.,
(e.g.,  ). Usually
). Usually  ; therefore,
; therefore,  must be nonzero, or quickly decrease to zero (e.g.,
must be nonzero, or quickly decrease to zero (e.g.,  ), where the former is a current sheet at the equator and the latter is a divergent current density (but weaker than the former).
), where the former is a current sheet at the equator and the latter is a divergent current density (but weaker than the former).
Footnotes
- 5
A few families of exact solutions (e.g., Menon & Dermer 2005, 2007, 2011; Brennan et al. 2013; Menon 2015; Compère et al. 2016) to the equations of force-free electrodynamics in the Kerr spacetime have been found in the past decade. But these solutions have various limitations, e.g., not allowing energy extraction from the BH, being electrically dominated instead of magnetically dominated, lacking clear physical interpretation, or being time dependent and not axisymmetric, which make it difficult to compare these exact solutions with simulations and numerical solutions.
- 6
It is definitely worthwhile to examine the solution uniqueness problem of the BZ mechanism, considering its significance in the modern relativistic astrophysics. For example, rotating BHs are believed to be described by the Kerr solution, but there is no solid evidence for it. Some efforts have been made to detect possible deviation from the Kerr solution via BZ mechanism powered jet emission (e.g., Bambi 2012a, 2012b, 2015; Pei et al. 2016). A prerequisite for these BZ applications is its solution uniqueness.
- 7
The stability problem of general force-free jets is a complicated story. Early studies implied that the force-free jets are vulnerable to various instabilities (e.g., Begelman 1998; Lyubarskii 1999; Li 2000; Wang et al. 2004), while later studies showed that these instabilities are strongly suppressed by field rotation, poloidal field curvature, etc. (e.g., Tomimatsu et al. 2001; McKinney & Blandford 2009; Narayan et al. 2009, and references therein).
- 8
- 9
The claim depends on the relation
 , which can be derived from the radiation condition at infinity [Equation (6)]. But their are some debates about whether the radiation condition holds for vertical field configurations. As for the uniform field, there is no disagreement on the relation
, which can be derived from the radiation condition at infinity [Equation (6)]. But their are some debates about whether the radiation condition holds for vertical field configurations. As for the uniform field, there is no disagreement on the relation  (Equation (8)), though Pan & Yu (2016) interpreted it as the result of the radiation condition, while Nathanail & Contopoulos (2014) interpreted it differently.
(Equation (8)), though Pan & Yu (2016) interpreted it as the result of the radiation condition, while Nathanail & Contopoulos (2014) interpreted it differently. - 10
The convergent solution is independent of the trial field configuration or the grid resolution. For example, we tested different initial field configurations
 , different initial trial functions Ω and I, and different grid resolutions.
, different initial trial functions Ω and I, and different grid resolutions.








