Abstract
The Kleinmann–Low nebula in Orion, the closest region of massive star formation, harbors Source I, whose nature is under debate. Knowledge of this source may have profound implications for our understanding of the energetics of the hot core in Orion KL since it might be the main heating source in the region. The spectral energy distribution of this source in the radio is characterized by a positive spectral index close to 2, which is consistent with (i) thermal bremsstrahlung emission of ionized hydrogen gas produced by a central massive protostar, or (ii) photospheric bremsstrahlung emission produced by electrons when deflected by the interaction with neutral and molecular hydrogen like Mira-like variable stars. If ionized hydrogen gas were responsible for the observed continuum emission, its modeling would predict detectable emission from hydrogen radio recombination lines (RRLs). However, our SMA observations were obtained with a high enough sensitivity to rule out that the radio continuum emission arises from a dense hypercompact H ii region because the H26α line would have been detected, in contrast with our observations. To explain the observational constraints, we investigate further the nature of the radio continuum emission from source I. We have compared available radio continuum data with the predictions from our upgraded non-LTE 3D radiative transfer model, MOdel for REcombination LInes, to show that radio continuum fluxes and sizes can only be reproduced by assuming both dust and bremsstrahlung emission from neutral gas. The dust emission contribution is significant at ν ≥ 43 GHz. In addition, our RRL peak intensity predictions for the ionized metals case are consistent with the nondetection of Na and K RRLs at millimeter and submillimeter wavelengths.
Export citation and abstract BibTeX RIS
1. Introduction
The highly extinguished (Lagrange et al. 2004) infrared region of the Kleinmann–Low (KL) nebula in Orion is the most luminous object within the Orion Molecular Cloud (Kleinmann & Low 1967) and one of the regions with the largest number of protostellar objects (at least 20 compact sources with a strong infrared emission detected; Gezari et al. 1998). Its distance has been measured based on trigonometric parallax. In particular, multiepoch observations of strong SiO (Kim et al. 2008) and H2O (Hirota et al. 2007) maser spots are consistent with a distance of 418 pc. However, recent radio observations of the emission of low-mass stars suggest that it might be closer, at a distance of 388 ± 5 pc (Kounkel et al. 2017).
This region shows all kinds of signposts of massive star formation (>8 M☉), such as H2O masers, compact H ii regions, and a hot core. In fact, the large luminosity of this complex of sources, L ≥ 105 L⊙ (Gezari et al. 1998), is by itself a strong indication of the presence of massive star formation. Thus, it is clearly the closest region where massive star formation is currently taking place. These characteristics make it one of the most studied regions in our Galaxy, and the ideal source to study the poorly understood processes taking place in high-mass star formation. In particular, radio continuum images show three compact sources that are thought to be massive young stellar objects (MYSOs): the very young Becklin–Neugebauer object (BN; Becklin & Neugebauer 1967; Beuther et al. 2005, 2006), the relatively evolved YSO known as Source n (Greenhill et al. 2004), and our target source, Orion Source I (hereafter Orion I), which is adjacent to the hot core (see, e.g., Wright & Plambeck 2017).
Orion I has a very faint counterpart in the near-infrared wavelengths but has no detectable emission in the optical wavelengths (Sitarski et al. 2013), which suggests that it is deeply embedded in dust and thus affected by high extinction. However, it clearly stands out as the brightest radio continuum source after the BN object (Rodríguez et al. 2009). High-resolution observations have shown that its radio continuum emission is elongated (Reid et al. 2007; Rodríguez et al. 2009; Goddi et al. 2011; Plambeck & Wright 2016). A puzzling question is the interpretation of the nature of this emission. The spectral energy distribution (SED) at centimeter, millimeter, and submillimeter wavelengths shows a positive spectral index. Initially, it was thought to be originated by bremsstrahlung due to the electrostatic interaction between the free electrons and protons in a dense H ii region. This idea was favored because this type of emission is commonly found toward pre-main-sequence massive stars (e.g., Marsh et al. 1976). However, several attempts of detecting the hydrogen radio recombination lines (RRLs) emitted by this hypothetical dense H ii region have failed (Plambeck et al. 2013; Plambeck & Wright 2016).
An alternative explanation to the measured spectral index would be that Orion I is a Mira-like variable star. Under this assumption, the radio continuum emission would be due to bremsstrahlung of electrons when deflected by the interaction with neutral atomic and molecular hydrogen (these species are denoted as H i and H2). This kind of emission has been observed in the cool and dense atmospheres of Mira variable stars (Reid & Menten 1997). Although this assumption requires very high densities of ∼1011 cm−3 in a neutral disk at Te ∼ 1600 K (Plambeck et al. 2013) to explain the radio continuum fluxes measured toward Orion I, it provides a straightforward explanation to the measured spectral index assuming power-law electron density gradients consistent with a neutral atmosphere in hydrostatic equilibrium (Reid et al. 2007). In addition, optical interferometric observations have revealed that some Mira variable stars also have elongated morphologies (Lattanzi et al. 1997). Thus, the observed radio continuum emission toward Orion I might be interpreted as due to a dense neutral disk around a massive star, or even as the atmosphere of a Mira variable star.
First, Beuther et al. (2006) suggested that a dense H ii region would explain the radio continuum emission at low frequencies, ν < 43 GHz, while emission of dust, located around the H ii region, would explain the emission at higher frequencies. More recently, Plambeck & Wright (2016) have arrived at the same conclusion based on the assumption that dense neutral gas in a disk could not explain the turnover frequency at ν > 600 GHz with reliable masses for the disk. Therefore, there is no consensus about the nature of Orion I yet. We note that establishing the nature of Orion I may have profound implications for our understanding of how the hot core in Orion KL is heated. If Orion I were a massive star, it could be responsible for the heating as initially proposed by Wright et al. (1992). However, other alternatives have been proposed, such as heating produced by the IR sources IRC2 (Genzel & Stutzki 1989), by internal protostars (de Vicente et al. 2002), or by an explosive flow (Zapata et al. 2011).
In this paper, we aim to provide insight into the nature of Orion I. For this, we have performed SMA5 observations (described in Section 2) to measure the hydrogen RRLs at 353.6 GHz. Then, we have proceeded to carefully model all available data at radio wavelengths for this source (presented in Section 3) by using the upgraded version of the MOdel for REcombination LInes (MORELI) code (see Section 4). The results of our modeling, considering different assumptions about the nature of Orion I, are reported in Section 5. We discuss in Section 6 the consequences of our constraints on the nature of Orion I for understanding the heating of the hot core in Orion KL, and in Section 7 we present our conclusions.
2. SMA Observations and Data Reduction
The SMA observations were performed on 2014 August 28. We used the dual-receiver mode by tuning the 345Rx and 400Rx receivers simultaneously to the frequency of the H26α line at 353.623 GHz. The observations were carried out in Extended (EX) configuration to filter out, as much as possible, the extended emission around Orion I. The corresponding resolution also helps us avoid molecular contamination due to the nearby hot core located at a distance of ≈2 arcsec and the extended molecular emission found in the nearby regions (Genzel & Stutzki 1989; Chandler & Wood 1997). The ASIC correlator provided a total bandwidth of 4 GHz per receiver and covered the frequency ranges from 342.74 to 344.73 GHz and from 352.75 to 354.74 GHz. The position of phase center of the observations was  , δJ2000 = −05°22'30
, δJ2000 = −05°22'30 56, i.e., the coordinates of Orion I. The radial velocity of the source was fixed at VLSR = 5 km s−1. We used a uniform spectral resolution of 0.8 MHz, which provided a velocity resolution of ∼0.7 km s−1 at the frequency of the H26α line. Data calibration was carried out within the IDL MIR software package, and continuum subtraction, imaging, and deconvolution were done within MIRIAD. The uncertainty in the flux calibration was within 20%.
56, i.e., the coordinates of Orion I. The radial velocity of the source was fixed at VLSR = 5 km s−1. We used a uniform spectral resolution of 0.8 MHz, which provided a velocity resolution of ∼0.7 km s−1 at the frequency of the H26α line. Data calibration was carried out within the IDL MIR software package, and continuum subtraction, imaging, and deconvolution were done within MIRIAD. The uncertainty in the flux calibration was within 20%.
To ensure that the continuum emission observed in the direction of Orion I was truly associated with this source and presented as little contamination as possible from the surrounding envelope, we imaged the continuum emission by using the data with baselines longer than 150 kλ and uniform weighting. The new synthesized beam was 0 70 × 0
70 × 0 41, PA = −74
41, PA = −74 21. The measured flux of Orion I is 430 ± 27 mJy, consistent with that obtained by Beuther et al. (2004) at similar frequencies.
21. The measured flux of Orion I is 430 ± 27 mJy, consistent with that obtained by Beuther et al. (2004) at similar frequencies.
The H26α line was imaged by using the original angular resolution of 0 8 × 0
8 × 0 6 and natural weighting. The original rms noise level in the data cube was 99 mJy beam−1. However, since the line width of the RRL should be at least as large as the thermal broadening (i.e., ∼15 km s−1), we smoothed the spectra in the H26α data cube to a velocity resolution of 10 km s−1. Using MADCUBA,6
we then extracted the H26α spectrum from a region of the same size as the beam centered at the position of Orion I. This pushed down the rms noise level to 22 mJy beam−1.
6 and natural weighting. The original rms noise level in the data cube was 99 mJy beam−1. However, since the line width of the RRL should be at least as large as the thermal broadening (i.e., ∼15 km s−1), we smoothed the spectra in the H26α data cube to a velocity resolution of 10 km s−1. Using MADCUBA,6
we then extracted the H26α spectrum from a region of the same size as the beam centered at the position of Orion I. This pushed down the rms noise level to 22 mJy beam−1.
3. Other Observational Data
3.1. Spectral Energy Distribution
We have compiled the complete set of observations performed so far toward Orion I with high enough spatial resolutions, θFWHM < 1.5 arcsec, to clearly separate Orion I from the nearby hot core. We show the compiled data in Appendix A and Table 5. The measured SED, plotted in Figure 1, clearly shows a scatter in the measured values for observations at the same, or similar, frequencies. In some cases, it is due to the different spatial resolutions of the observations. For example, our radio continuum flux measured at 353.74 GHz is half that measured using ALMA (Plambeck & Wright 2016) and consistent with other SMA observations (Beuther et al. 2004). This suggests that our observations lack a high enough number of baselines to recover all the emission of Orion I (Bajaja & van Albada 1979). For this reason, we will consider in the SED the measurements provided by the ALMA observations at this particular frequency. However, a fraction of the scatter may also be due to the variable nature of this source as reported by Rivilla et al. (2015).
Figure 1. Computed SEDs (lines) and observational data measured (points with error bars) for Orion I. The observational data were obtained from the references shown in Table 5. The dashed and solid lines show the MORELI predictions for a neutral disk without and with dust emission, respectively (see Section 4.1), and only for the models with bt = 0.42 for clarity of presentation. We have used the values shown in Table 2 as input parameters.
Download figure:
Standard image High-resolution imageDespite the mentioned scatter, the average value of the SED is clearly consistent with a positive spectral index. In particular, it is consistent with a spectral index of7 1.71 ± 0.18 (with a correlation coefficient of r = 0.98) for the range of low frequencies, i.e., ν < 100 GHz. At higher frequencies, the spectral index increases slightly, as expected for an additional contribution from dust. Thus, at least two different sources of continuum emission seem to be required to fit the SED at sub/millimeter wavelengths.
3.2. Morphology of the Radio Continuum Emission
Our SMA observations do not resolve the structure of Orion I. Therefore, we have analyzed its geometry with the data compiled from previously published interferometric data. All the radio continuum maps resolving Orion I are consistent with a disk geometry, viewed almost edge-on, which can be characterized by the sizes of its major and minor axes. It is worth noting that the virtually edge-on disk with respect to the line of sight is also consistent with the results of the modeling of its near-IR counterpart (Sitarski et al. 2013) and the interpretation of the SiO maser emission distribution (Matthews et al. 2010).
The measured deconvolved angular sizes are shown in Table 1 and plotted in Figure 2. The size of the minor axis of Orion I appears to be constant for the whole frequency range. On the contrary, the size of the major axis clearly varies with the frequency. In particular, it decreases from 190 mas at 8.3 GHz to 90 mas at 43 GHz, and then, at submillimeter wavelengths, it increases up to a size of ∼230 mas, consistent with the size measured at 8.3 GHz.
Table 1. Deconvolved Angular Sizes of Orion I Measured with Radio Interferometers
| Frequency | Major Axis | Minor Axis | Synthesized Beam | References |
|---|---|---|---|---|
| ν (GHz) | θmaj (mas) | θmin (mas) | θFWHM (mas × mas) | |
| 8.3 | 190 ± 40 | ≤150 | 260 × 250 | Gómez et al. (2008) |
| 43 | 90 ± 10 | 60 ± 20 | 170 × 150 | Rodríguez et al. (2009) |
| 229 | 210 ± 20 | 60 ± 50 | 180 × 150 | Plambeck & Wright (2016) |
| 349 | 230 ± 20 | 30 ± 50 | 250 × 180 | Plambeck & Wright (2016) |
| 440 | 216.7 ± 1.6 | 53.0 ± 1.2 | 83 ± 67 | Hirota et al. (2016) |
| 460 | 220.4 ± 1.8 | 52.3 ± 1.8 | 104 ± 87 | Hirota et al. (2016) |
| 490 | 218.9 ± 1.5 | 50.9 ± 1.7 | 111 ± 79 | Hirota et al. (2016) |
| 661 | 250 ± 10 | 60 ± 30 | 160 × 120 | Plambeck & Wright (2016) |
Download table as: ASCIITypeset image
Figure 2. Observed (filled circles with error bars) and computed (lines) sizes at half-maximum full width for Orion I. The MORELI predictions without taking into account the dust emission (dashed line) reproduce the sizes at ν < 100 GHz, while those obtained assuming that the dust emission is not negligible (solid line) also fit the measured sizes at submillimeter wavelengths. We note that the values obtained with MORELI using the three different sets of input parameters match closely with each other. For this reason, and for clarity of presentation, we only plot the case of bt = 0.42. The references for the observational data are shown in Table 1.
Download figure:
Standard image High-resolution imageThe different dependence of the size of the major axis on the frequency for values lower and higher than ∼100 GHz provides additional support to the presence of at least two different components of radio continuum emission. In fact, the constant size at high frequencies is, in principle, consistent with the emission of a dusty disk of that size. As discussed in Section 5, the decrement of the size with the frequency as  at low frequencies will be key to discriminating between the different processes responsible for this emission.
at low frequencies will be key to discriminating between the different processes responsible for this emission.
3.3. Brightness Temperature Profile
In addition to radio continuum sizes, the brightness temperature of the resolved radio continuum emission is another essential parameter for understanding the nature of Orion I. Its variation along the major axis has been measured at 43 GHz with a spatial resolution of 34 mas as shown by Reid et al. (2007) in their Figure 3. Its most remarkable feature is that it reaches a value of about 1600 K in the central region, while it falls virtually to zero at radii of ∼65–85 au (these values were estimated by scaling the results to a distance of 388 pc). We remark that this value is consistent with the full size of the major axis, 210 ± 10 mas, measured by Goddi et al. (2011). On the other hand, the peak brightness temperature significantly decreases to values of ∼750 K at ν ∼ 460 GHz according to very recent ALMA observations (Hirota et al. 2016).
3.4. Spectra at Frequencies of RRLs
We have carefully checked for emission of detectable RRLs in our spectrum taking into account the systemic velocity of Orion I, VLSR = 5 km s−1, as measured from molecular lines (Plambeck & Wright 2016). As shown in Figure 3, our SMA spectra do not show any hints of the H26α RRL. Thus, we rule out that its intensity is higher than ∼70 mJy, i.e., about three times the rms noise level achieved in our observations by smoothing the spectrum to a velocity resolution of 10 km s−1. This result is also consistent with that found by Plambeck & Wright (2016). In particular, they could detect neither the H26α nor the H21α, giving as upper limits for their peak intensities ≈100 and 375 mJy, respectively.
Figure 3. SMA spectrum of the H26α line measured within a region of the same size as the beam toward Orion I. The local standard of rest of the source is vLSR = 5 km s−1 (see vertical dotted line; Plambeck & Wright 2016). The spectrum was smoothed to a spectral resolution of 10 km s−1, and the measured rms noise level is 22 mJy. The horizontal dashed line indicates the 3σ level in the spectrum. No emission of the H26α line is detected above this level.
Download figure:
Standard image High-resolution imageOnce we have excluded the detection of Hnα RRLs, we have looked for any hint of the presence of metal RRLs for those elements expected to be strongly ionized because of the measured peak brightness temperature and their low ionization potential. Among these elements, potassium and sodium (with ionization potentials of ≈4.34 and 5.14 eV, respectively) are those that supply most of the free electrons given their high relative abundances with respect to hydrogen atoms: NK/NH ≈ 1.1 × 10−7 and NNa/NH ≈ 1.7 × 10−6, where NK, NNa, and NH are the densities of K, Na, and H atoms, respectively (Asplund et al. 2009). In particular, potassium is the most abundant ionized element for temperatures lower than ≈1500 K, while the abundance of ionized sodium becomes relevant for higher temperatures, dominating the number of ionized atoms over those of potassium for T > 1700 K (Reid & Menten 1997). The collisional ionization of other elements with relatively high abundances, such as calcium and aluminum, is negligible except for higher temperatures.
As discussed in Appendix B, the sodium and potassium RRLs should appear at frequencies shifted, in velocity, by 156.11 and 159.05 km s−1 toward lower frequencies with respect to the same transitions of hydrogen (and at the same vLSR because all these RRLs probe the same regions). However, we have not found any hint of these metal RRLs in any spectra. Given that the achieved rms in the ALMA spectra is better than that obtained in our SMA spectrum (if it is smoothed to the spectral resolution of the published ALMA spectral, ∼1.7 km s−1; Plambeck & Wright 2016), we can provide 90 and ∼375 mJy as upper limits for the peak intensities of metal RRLs taking into account that their thermal broadening is expected to be ≈2 km s−1.
4. The Expanded MORELI Code, a MOdel for REcombination LInes and Radio Continuum Emission
We have used the MORELI code to constrain the physical properties of the disk in Orion I assuming a distance of 388 pc (see Section 1). As extensively described in Báez-Rubio et al. (2013), this code assumes different geometries and physical and kinematic structures to predict the hydrogen RRL profiles for local thermodynamic equilibrium (LTE) and non-LTE conditions. It also predicts the continuum emission due to bremsstrahlung by electrons and protons and to bound-free transitions. The code performs the 3D radiative transfer through all the lines of sight in a grid with nx × ny pixels. Thus, it is a key tool to constrain the characteristics of ionized regions. In particular, the electron density (Ne) and electron temperature (Te) distributions are parameterized as power laws specified by indices bd and bt, respectively, i.e.,  and
and  (see Báez-Rubio et al. 2013). The possible angular dependence of the electron density has been neglected when modeling the radio continuum emission of Orion I.
(see Báez-Rubio et al. 2013). The possible angular dependence of the electron density has been neglected when modeling the radio continuum emission of Orion I.
In order to explore the nature of Orion I, we have upgraded the code to include new sources of continuum opacities, whose emission might be significant for predominantly neutral regions such as the dust emission and the bremsstrahlung contribution produced when free electrons, generated after the collisional ionization of metals, are deflected by their electrostatic interaction with molecular hydrogen and neutral hydrogen. In the following, we describe in detail how these processes are modeled by MORELI.
4.1. Collisional Ionization
The MORELI code performs the radiative transfer for modeling a predominantly neutral region in the same way as for an H ii region. However, for the former case, MORELI assumes the density distribution of hydrogen atoms with the same power law as that assumed for the electron density for an H ii region, i.e.,  . Once the electron temperature and hydrogen density distributions are specified, MORELI estimates the collisional ionization for all the atomic elements with atomic numbers lower than that of nickel (Z = 28). For this, we assume that the ionization/recombination chemical reactions of the element with atomic number Z in the gas,
. Once the electron temperature and hydrogen density distributions are specified, MORELI estimates the collisional ionization for all the atomic elements with atomic numbers lower than that of nickel (Z = 28). For this, we assume that the ionization/recombination chemical reactions of the element with atomic number Z in the gas,

are under instantaneous chemical equilibrium, i.e., the forward and reverse reactions approximately proceed at the same rate, and therefore the abundances of the corresponding atomic element when it is ionized i and i + 1 times (these species are denoted as Zi and Zi+1, respectively) remain constant. In addition, we also assume that the ionization levels for each atomic element are populated according to LTE conditions, and therefore, following a Saha–Boltzmann distribution,

where k is the Boltzmann constant, me is the electron mass, h is the Planck constant, IZ,i is the ionization energy of the element Zi, and Ue,  , and
, and  are the partition functions of the electron and of the elements Zi and Zi+1, respectively. We note that Ue = 2, corresponding to two possible spin states for the electron. The values of the partition functions of the elements with atomic number Z were obtained from those derived by Irwin (1981), while the ionization potentials were obtained from the National Institute of Standards and Technology.8
are the partition functions of the electron and of the elements Zi and Zi+1, respectively. We note that Ue = 2, corresponding to two possible spin states for the electron. The values of the partition functions of the elements with atomic number Z were obtained from those derived by Irwin (1981), while the ionization potentials were obtained from the National Institute of Standards and Technology.8
We have obtained, for every pixel, the densities for all the elements singly ionized and neutral assuming an initial value for the electron density and, then, solving Equation (2) separately for each species. Thus, summing the electrons provided by each atomic element, we obtain a new value for the electron density. The procedure is iteratively repeated until the new electron density differs by less than 0.01% from the previous estimated value. We note that the chemical abundances are assumed to provide the electron densities. In particular, MORELI considers those provided by Asplund et al. (2009). On the other hand, the considered initial electron density depends on the dominant source providing the free electrons by thermal ionization. We assume that the dominant species are potassium for Te < 1600 K, sodium for 1600 K < Te < 6000 K, and hydrogen for Te > 6000 K.
4.1.1. Absorption Coefficients for the Gas
The free electrons provided by collisional ionization will be a source of opacity due to bremsstrahlung by their interaction with protons, similarly to what occurs in H ii regions. The absorption coefficient for this physical process is described in Section 2.1.1 of Báez-Rubio et al. (2013). However, for a dense predominantly neutral disk of gas, the main sources of opacities are the bremsstrahlung by molecular and atomic hydrogen, whose values depend on the densities of these two species.
The densities of all the hydrogen species (i.e., the molecular, H2, atomic H i, ionized, H+, and the hydrogen anion9 , H−) are determined by the following two-body gas-phase chemical reactions:
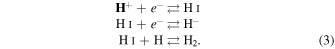
Since the total density of hydrogen atoms is an input parameter in the code, NH, we estimate the densities of all the species of hydrogen based on the electron density obtained by the previously described method (Section 4.1) and on the ratios between all the species of hydrogen, assuming thermal equilibrium conditions and that the ionization of neutral hydrogen is negligible. In particular, in this case, the density of the negative ion of hydrogen,  , is related to the total density of atomic hydrogen, NH i, as follows:
, is related to the total density of atomic hydrogen, NH i, as follows:
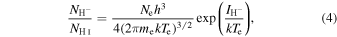
where  is the binding energy of the negative ion of hydrogen, which is 0.75420375 ± 0.0000003 eV (Andersen et al. 1999). This expression has been obtained taking into account UH i = 2 and
is the binding energy of the negative ion of hydrogen, which is 0.75420375 ± 0.0000003 eV (Andersen et al. 1999). This expression has been obtained taking into account UH i = 2 and  in Equation (2). This equation can be parameterized, considering Ne and Te in units of 1010 cm−3 and 1000 K, respectively, as follows:
in Equation (2). This equation can be parameterized, considering Ne and Te in units of 1010 cm−3 and 1000 K, respectively, as follows:

On the other hand, the ratio between the densities of molecular,  , and atomic hydrogen, NH i, are obtained with a similar expression to that shown in Equation (2), which relates the abundances of the different degrees of ionization for each element, but with the difference that we must use the dissociation energy of the molecular hydrogen,
, and atomic hydrogen, NH i, are obtained with a similar expression to that shown in Equation (2), which relates the abundances of the different degrees of ionization for each element, but with the difference that we must use the dissociation energy of the molecular hydrogen,  eV (Sprecher et al. 2011), as follows:
eV (Sprecher et al. 2011), as follows:
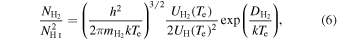
where  is the mass of the molecular hydrogen. If this equation is parameterized like Equation (4), one obtains
is the mass of the molecular hydrogen. If this equation is parameterized like Equation (4), one obtains
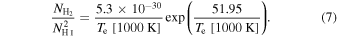
Taking into account that the sum of all the species is equal to the number of hydrogen atoms, i.e.,  , we derive the density of atomic hydrogen, and subsequently the densities of the rest of species, as follows:
, we derive the density of atomic hydrogen, and subsequently the densities of the rest of species, as follows:
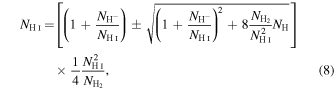
where the fractions between densities are obtained from the electron temperature and atomic parameters with Equations (4) and (6).
Once the densities of all the species are known, we derive the absorption coefficients for the bremsstrahlung due to molecular and atomic hydrogen,  and κH i, respectively, by using the analytical expressions derived by Reid & Menten (1997) to fit the numerical values obtained by Dalgarno & Lane (1966):
and κH i, respectively, by using the analytical expressions derived by Reid & Menten (1997) to fit the numerical values obtained by Dalgarno & Lane (1966):

where ν is the frequency in units of 10 GHz, while  and
and  are given in SI units by the relations
are given in SI units by the relations
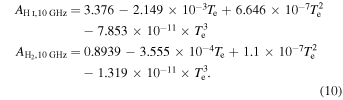
It is interesting to note that both sources of opacity are significant, in dense H i regions, when they have temperatures above ∼1000 K. The absorption coefficients for both sources of opacities are such that the bremsstrahlung due to molecular hydrogen dominates over that due to neutral hydrogen for temperatures above ∼1500 K. We note that the opacity of the ion H− can be neglected at radio wavelengths given its much lower density with respect to the atomic hydrogen, as one deduces from Equation (4).
4.2. Dust Emission
The upgraded MORELI code allows us to consider the dust emission in those pixels where the dust temperature is assumed to be lower than 1700 K, since at higher temperatures dust is expected to sublimate (D'Alessio et al. 1999). It is remarkable to note that, at solar metallicities, dust and gas temperatures are well coupled by collisions for densities above 105 cm−3 (Burke & Hollenbach 1983; Goldsmith 2001; Glover & Clark 2012), which are similar to those found in the disk of Orion I (Section 5.2). For this reason, even if MORELI can assume different profiles for the dust and electron temperatures, we have assumed Tdust = Te for the modeling of Orion I. Thus, the integration of the radiative transfer equation (Equation (2) of Báez-Rubio et al. 2013) is solved by adding a new term to the optical depth due to dust emission. Its absorption coefficient is estimated according to the following formula:

where κν is the dust absorption coefficient normalized to its mass, R is the gas-to-dust mass ratio, and mH is the average mass of the hydrogen atom, which has a value of mH = 1.007975 ± 0.000135 uma (Meija et al. 2013).
We have assumed the normalized dust opacities, κν, provided by Ossenkopf & Henning (1994) based on a coagulation model for the dust grains. MORELI incorporates the absorption coefficients for different types of materials such as dust without ice mantles, with thin ice mantles, or with thick ice mantles. The absorption coefficients at frequencies higher than 230.66 GHz are extrapolated assuming a dependence with the frequency of  , where βd has a value of about 1.75 for dust with thick ice mantles.
, where βd has a value of about 1.75 for dust with thick ice mantles.
We note that the considered values for both the dust sublimation temperature, Ts,dust, and the absorption coefficients are a rough approximation because we ignore what materials form the disk in Orion I. However, the high densities derived for the disk of Orion I (Section 5.2) make probable the presence of thick ice mantles on the grains.
5. The Nature of Orion I
In the following section, we explain in detail how the observational results (Section 2) provide constraints on the nature of the radio continuum emission observed toward Orion I. In Section 5.1, we show that the physical structure required to fit the radio continuum data is not consistent with the observational data if a dense H ii region is considered. Alternatively, we explore the hypothesis that the radio continuum emission is due to a neutral dense disk with significant emission by bremsstrahlung due to H2 and H−, as well as by dust at high frequencies (Section 5.2).
5.1. Is Orion I an Ultracompact H ii Region?
(i). Model with a dense H ii region with no dust emission
The SED at centimeter and millimeter wavelengths (Section 3) could be explained as due to a massive protostar ionizing its closest environment and forming an ionized wind. In such a case, the continuum emission would be produced by partially optically thick thermal bremsstrahlung by the interaction between electrons and protons. In principle, this model could explain the measured SED, with a spectral index of ≈1.85. However, it would require a presumably unrealistic density gradient of Ne ∝ r−6. In addition, a dense H ii region predicts a much higher brightness temperature, of ∼10,000 K, than that measured at 43 GHz in the central region of the radio continuum emission (Section 3.3). The same problem would arise if we assume that a dense homogeneous H ii region was responsible for that emission. Thus, we rule out that a dense H ii region, without dust, could explain the radio continuum emission at ν ≥ 43 GHz.
(ii). Model with a dense H ii+dusty region
We have also explored as a possibility that the emission at low frequencies, ν < 43 GHz, is due to bremsstrahlung by a dense H ii region, but with significant dust emission and optically thin bremsstrahlung emission (whose contribution to the SED follows a spectral index of ≈−0.1) at higher frequencies. In this case, the bremsstrahlung emission could show a turnover frequency, i.e., the transition frequency between partially optically thick and optically thin emission, at ν < 661 GHz (frequency at which there is a significant rise in the SED interpreted as due to dust emission; see Section 3.1), and the contribution from dust could increase significantly at millimeter/submillimeter wavelengths.
If the bremsstrahlung turnover frequency occurred at ≈43 GHz, as proposed by Plambeck & Wright (2016), then the bremsstrahlung emission due to the interaction between electrons and protons would contribute to the measured radio continuum flux at ν > 43 GHz in ∼10 mJy. In this case, the expected peak intensities of the H26α and H21α RRLs would show, respectively, values of ≈40 and 80 mJy for LTE conditions at 10,000 K (which implies velocity-integrated line-to-continuum ratios of 114 and 235 km s−1, respectively10 ) and negligible dynamical broadening. These values would exceed the observed ones except for dynamical broadening greater than 100 km s−1. However, this condition seems very unlikely given that the geometry of its elongated emission does not seem to correspond to the one expected in a collimated jet like those observed in high-velocity jets around massive stars (e.g., Jiménez-Serra et al. 2011). In addition, as previously discussed, under this hypothesis the peak brightness temperature would show a value close to 10,000 K at 43 GHz (where dust emission does not play an important role), significantly higher than the ≈1600 K measured.
5.2. Studying the Emission of a Neutral Disk toward Orion I
Once it has been ruled out that a dense ionized region could explain the radio continuum emission at ν ≤ 43 GHz, we explore the possibility that it is due to a neutral disk as originally proposed by Reid et al. (2007). In this case, its radio continuum emission could be due to different physical processes (see Section 4): (i) H i and H2 bremsstrahlung emission, and/or (ii) dust emission.
As claimed by Plambeck & Wright (2016), dust emission could be significant at millimeter and submillimeter wavelengths, explaining the increase of the spectral index measured in the SED at high frequencies (see Figure 1). However, in no case could it explain the observational data at low frequencies, such as the observed size of the radio continuum emission at 43 GHz, or the brightness temperature of ∼1600 K measured where that emission peaks. Alternatively, we favor the scenario that radio continuum emission at ν ≤ 43 GHz is mainly due to H i and H2 bremsstrahlung emission. We have used the MORELI code to check whether this assumption is consistent with the observations.
The spectral index is well reproduced by MORELI even if one assumes smooth density gradients, unlike what is required in the scenario that the emission arises from an H ii region. However, since the SED can be fitted with different electron density gradients, we have constrained it based on the observational brightness temperature profile along the major axis of the disk at 43 GHz and the peak brightness temperature at ∼460 GHz (see Section 3.3).
Independent of which physically reasonable electron temperature and density distributions were assumed, the brightness temperature predicted by MORELI falls sharply at radii higher than a particular radius where the continuum emission of the H i region becomes optically thin. This occurs because at that radius the density drops below the threshold value at which there are not enough free electrons to make significant the opacity of the neutral and molecular hydrogen bremsstrahlung. Thus, one can consider this radius as the size of a radio photosphere, rph. The observational data (Section 3.3) show a relatively gentle decrement with increasing radii given the poor spatial resolution of the observations (θHPBW = 34 mas). Thus, we have reproduced the brightness temperature profile performing the radiative transfer with high enough spatial resolution to resolve the size of the radio atmosphere, and afterward we have convolved the brightness in the plane of the sky within box filters with the same spatial area as the half-power beam width (HPBW) of the observations.
The measured brightness temperature profile has been modeled assuming the prototypical electron density gradient of a wind, bd = −2, and considering electron temperature gradients (see Section 4) with bt of 0.5, 0.42, and 0.34. Shallower electron temperature gradients can be ruled out because they would overestimate the SED at the highest observed frequency, 690 GHz. The electron temperature is set at a value of ∼1600 K at rph, independent of its temperature gradient, to reproduce the brightness temperature within the radio photosphere. We note that the measured size of the radio continuum emission at 43 GHz provides a rough measurement of the size of the radio photosphere, i.e., rph ∼ 20 au. Therefore, we could constrain the density at rph, ensuring that it is high enough to fit the radio continuum emission at 43 GHz. Finally, we have provided further constraints to the electron density gradient by imposing that the radio continuum emission should not be negligible up to radii as high as ≈60 au. Thus, as shown in Figures 1, 2, and 4, we have reproduced the observational data by using the three sets of input parameter values shown in Table 2.
Figure 4. Estimated brightness temperature profiles along the major axis at 43 GHz for Orion I assuming three different temperature gradients, bt. These profiles have been derived by using the input parameters shown in Table 2 and convolving the original data within boxes of the same area as the HPBW (34 mas) of the observations provided by Reid et al. (2007).
Download figure:
Standard image High-resolution imageTable 2. Final Input Parameters for the Best Fit to the Continuum of Orion I Assuming a Cylindrical Geometry for the Neutral Disk with Dust
| Input Parameter | Electron Density Gradient | ||
|---|---|---|---|
| bt = 0.50 | bt = 0.42 | bt = 0.34 | |
| aInner radius, rmin (au) | 0.05 | 0.05 | 0.05 |
| Outer radius of the disk, rd (au) | 100 ± 15 | 100 ± 15 | 100 ± 10 |
| Height of the disk, ld (au) | 22.5 ± 6.5 | 22.5 ± 6.5 | 22.5 ± 6.5 |
| bDensity distribution, Ne(r) (cm−3) | (7.5 ± 4.5) × 1012 · r−2 | (7.50 ± 4.5) × 1012 · r−2 | (7.0 ± 4.0) × 1011 · r−2 |
| bElectron temperature, To (K) | (1790 ± 420) × r−0.50 | (1730 ± 360) × r−0.42 | (1680 ± 350) × r−0.34 |
Notes. Its inclination is assumed to be 0° based on the results of Kim et al. (2008) and Hirota et al. (2014).
aFor the three cases, an upper limit of ∼17 au (the radius where the brightness temperature profile falls as seen in Figure 4) can be considered. A nonzero value of rmin must be used to avoid singularities in the densities at r = 0. bTheir values are considered as a function of r, where it is in units of 20 au.Download table as: ASCIITypeset image
In particular, the models assume an edge-on cylindrical disk as indicated by the spatial pattern of the SiO masers (Kim et al. 2008) and the position–velocity diagrams of H2O masers (Hirota et al. 2014). The height of the disk is considered to be 22.5 ± 6.5 au (consistent with the minor axis length shown in Table 1 and with an uncertainty of half of the HPBW of the observation with the highest angular resolution carried out by Reid et al. 2007). In addition, we note that higher uncertainty values are ruled out because otherwise the SED would not be reproduced. On the other hand, a base radius of 100 au is considered to reproduce the radio continuum maps (Section 3.2). The density of hydrogen atoms reaches a value of ≈7.0 × 1011 cm−3 at a radius of 20 au. This model naturally explains the significant dust emission contributing to the radio continuum emission at ν > 50 GHz (see Figure 1). Since the dust emission occurs in the outer regions, with electron temperatures lower than the dust sublimation temperature (Section 4.2), it also allows us to reproduce the trend of the major axis size with increasing frequency (see Figure 2).
The models presented previously not only reproduce the radio continuum emission but also are consistent with the observational spectra (Section 3.4). We have assumed negligible dynamical broadening to predict lower and upper limits for the line widths and peak intensities of sodium and potassium RRLs. Our models predict absorption lines with line widths of about ∼2 km s−1 and the peak intensities shown in Table 3. These values are lower than 51 × 10−3 and 8.8 × 10−3 mJy for Na26α and K26α, respectively, i.e., clearly much lower than the achieved rms noise in our spectra. We note that even if we neglect dust absorption in the model (see Table 4), we would also predict peak intensities weaker than the achieved rms, in particular of ≈49 and 20 mJy, respectively. Likewise, the Na21α and K21α predicted peak intensities, with line widths of ∼2 km s−1, are below the rms noise of the ALMA data. In particular, in the case of neglecting dust emission, we obtain peak intensities of 370 and 110 mJy, respectively. If the dust emission is included, we would obtain absorption lines with peak intensities lower than ≈2 × 10−4 and 10−4 mJy, respectively. This is why they could not be detected either in our data or in the ALMA data. Thus, our model is consistent with the nondetection of the presumably strongest metal RRLs. We would like to stress that, given the weak metal RRLs predicted by MORELI after taking into account the dust contribution, follow-up spectroscopic measurements will not be expected to firmly confirm our predictions. However, if the Na21α RRL is not detected in spectra with a low rms noise, the data will clearly support our hypothesis that dust emission is not negligible at 43 GHz.
Table 3. Predicted Sodium and Potassium RRL Intensities (in mJy) for Transitions 26α and 21α
| Line | ν (GHz) | bt = 0.50 | bt = 0.42 | bt = 0.34 |
|---|---|---|---|---|
| Na26α | 353.80692 | 5.09 × 10−2 | 3.48 × 10−2 | 3.02 × 10−2 |
| K26α | 353.81039 | 0.88 × 10−2 | 0.73 × 10−2 | 0.83 × 10−2 |
| Na21α | 662.74915 | 1.91 × 10−4 | 1.11 × 10−4 | 1.20 × 10−4 |
| K21α | 662.75566 | 0.33 × 10−4 | 0.31 × 10−4 | 0.94 × 10−4 |
Note. The intensities were obtained assuming a spectral resolution of 1 km s−1 and the input parameters of our best models for the three temperature gradients, i.e., those described by the values shown in Table 2, considering both bremsstrahlung and dust emission.
Download table as: ASCIITypeset image
Table 4. Predicted Sodium and Potassium RRL Intensities (in mJy) for Transitions 26α and 21α
| Line | ν (GHz) | bt = 0.50 | bt = 0.42 | bt = 0.34 |
|---|---|---|---|---|
| Na26α | 353.80692 | 37.5 | 42.1 | 49.1 |
| K26α | 353.81039 | 13.7 | 16.7 | 20.4 |
| Na21α | 662.74915 | 300 | 330 | 370 |
| K21α | 662.75566 | 74.6 | 90.3 | 110 |
Note. The intensities were obtained assuming a spectral resolution of 1 km s−1 and considering the same models as those in Table 3 but neglecting the contribution from dust.
Download table as: ASCIITypeset image
Finally, we note that our density distribution is, in a first approximation, also consistent with the observed location of the discrete SiO maser features (Matthews et al. 2010). In particular, the  and
and  maser emissions are associated with a virtually edge-on disk (with an inclination of the axis of revolution with respect to the plane of the sky of 5°) at distances of 15–45 au and 20–55 au, respectively. The densities required for detecting maser emission of these two lines, according to the results from a radiative transfer modeling (Goddi et al. 2009), are ∼108–1010 cm−3 and ∼109–1011 cm−3, respectively. Given the high uncertainties of this model, which has not taken into account saturation effects and the effects of dust emission (Strelnitskii 1977), we consider that these results are consistent with the (5.3–71) × 1010 cm−3 densities assumed by our model in the regions traced by both lines.
maser emissions are associated with a virtually edge-on disk (with an inclination of the axis of revolution with respect to the plane of the sky of 5°) at distances of 15–45 au and 20–55 au, respectively. The densities required for detecting maser emission of these two lines, according to the results from a radiative transfer modeling (Goddi et al. 2009), are ∼108–1010 cm−3 and ∼109–1011 cm−3, respectively. Given the high uncertainties of this model, which has not taken into account saturation effects and the effects of dust emission (Strelnitskii 1977), we consider that these results are consistent with the (5.3–71) × 1010 cm−3 densities assumed by our model in the regions traced by both lines.
6. Evolutionary Stage of Orion I
Orion I was proposed to be the main source responsible for the heating of the infrared nebula around the KL nebula (Testi et al. 2010). Therefore, it could be responsible also for the heating of the hot core in Orion KL. However, our results favor that its radio continuum emission is mainly due to a neutral H i circumstellar disk that contains dust, hence ruling out the hypothesis that Orion I is the dominant heating source. This is consistent with very recent hints, from ALMA observations, that the hot core may be shock heated by the outflow from Orion I (Wright & Plambeck 2017). In addition, our results provide additional constraints on its possible evolutionary stage as discussed below.
The proper motions of Orion I and the BN object indicate that they were ejected about 500 yr ago from an explosive event (Gómez et al. 2005; Rodríguez et al. 2005, 2017), in which source X, an intermediate-mass star undetected at radio continuum wavelengths, was also involved (Luhman et al. 2017). It has been proposed that the explosive event could have been produced by the formation of a compact binary or merger (Bally et al. 2017). In fact, the kinematically determined masses of Orion I, with a value ranging from 5 to 9 M⊙ (Matthews et al. 2010; Plambeck & Wright 2016; Hirota et al. 2017), are consistent with the conservation of the linear momentum in the explosive event (Luhman et al. 2017). Thus, the intermediate- to high-mass hypothesis for Orion I is favored.
Based on this, it is highly probable that, like BN, Orion I was a young object, likely in the phase of generating an ultracompact H ii region. If this were the case, our results would hint that physical conditions in circumstellar disks around massive stars in formation are appropriate for significant bremsstrahlung emission by neutral and molecular hydrogen like in Mira-like variable stars. This would not be surprising if we take into account that high accretion rates could result in extended and cooler atmospheres so that the material around the photosphere has physical conditions that resemble those of evolved stars, as would be the case in the adiabatic accretion phase (Hosokawa & Omukai 2009).
However, SiO masers such as those observed toward Orion I (Kim et al. 2008; Matthews et al. 2010; Zapata et al. 2012; Greenhill et al. 2013; Hirota et al. 2014, 2017) have been detected in star-forming regions in some exceptional cases (Cho et al. 2016). Thus, as initially proposed by Reid et al. (2007), there is a chance that Orion I is not a star in formation but an evolved star. In fact, Mira-like variable stars show powerful SiO (e.g., Moran et al. 1979) and H2O (Rosen et al. 1978; Spencer et al. 1979) masers, such as those observed toward Orion I (H2O masers were detected by Genzel et al. 1981; Gaume et al. 1998; Hirota et al. 2007, 2012, 2014, 2017; Kim et al. 2008; Matthews et al. 2010; Greenhill et al. 2013). In addition, the luminosity of Orion I, L ≳ 104 L⊙ (Menten & Reid 1995), would be consistent with that expected for Mira variable stars with masses of ≳4 M⊙ as indicated by stellar evolutionary track models (Ferrarotti & Gail 2006). However, we note that their luminosities are observationally poorly constrained (Hinkle et al. 2016). On the other hand, the bipolar structure and kinematics of the SiO and H2O masers in Orion I resemble those observed in O-rich protoplanetary nebula like OH231.8 + 4.2 (Sánchez Contreras et al. 2002). The evolved nature of Orion I is supported not only by the fact that Mira variable stars emit those masers but also because they are the only detected sources dominated by bremsstrahlung emission by neutral and molecular hydrogen in their dense H i radio atmospheres (Reid & Menten 1997). All the findings mentioned above and the absence of an H ii region would hint that Orion I could be an evolved star in the very early stages of the protoplanetary nebula phase. Therefore, it might be the first known massive star in the post-AGB phase.
Nevertheless, how could we reconcile an evolved nature with the explanation of the explosive event occurring ∼500 yr ago? Rivilla et al. (2013) have found the presence of low-mass star clusters associated with the massive star formation in the Orion hot core and argued that it is undergoing competitive accretion to form a massive star cluster. In this scenario merging will play a role in the formation of the most massive stars in the cluster, likely giving rise to explosive events like that observed from the ejection of BN and Orion I. The strong potential well of the low-mass star cluster could also capture field stars that will interact gravitationally with the objects in the cluster. In this scenario Orion I would be an evolved star captured by the cluster that might have provided the energy to trigger the explosion. However, as previously discussed, one cannot completely rule out that Orion I is a young massive star. With the available data, it is so far impossible to unambiguously establish the evolutionary stage of Orion I, even if the reported continuum emission seems clearly not to be emitted by an H ii region.
7. Conclusions
The main result of our work is to gain insight into the nature of Orion I by combining the radio continuum and RRL emission observations, obtained with the VLA, the SMA, and ALMA, with the 3D radiative transfer modeling of this source performed with the MORELI code. The nondetection, with rms values of the order of 22 mJy reported in Section 2, of the H26α and H21α RRLs with the SMA observations described in this paper and also with the ALMA data provided by Plambeck & Wright (2016) supports the absence of a dense H ii region responsible for the radio continuum emission at ν ≤ 43 GHz.
Therefore, we have upgraded our MORELI code to model the bremsstrahlung processes due to a predominantly neutral H i and H2 disk (see Section 4.1) that contains dust. Our models show that these different types of emission are required to explain the decreasing sizes of Orion I observed between 8 and 43 GHz, while the dust emission significantly contributes to the emission at ν ≥ 43 GHz. In addition, our model prediction is consistent with the nondetection of hydrogen and metal RRLs produced by collisional ionization. Thus, we conclude that our modeling firmly establishes that the radio continuum emission observed toward Orion I is due to a combination of dust emission and bremsstrahlung by interaction between the free electrons and molecular and atomic hydrogen in a very dense disk. In addition, our modeling predicts that one should expect to detect some Na RRLs, e.g., with intensities of about ∼0.26 mJy for Na34α, if one performs long observations with ALMA (or the order of 100 hr). If these RRLs are detected in the future, they will become the definite test of the nature of the radio continuum emission toward Orion I.
Finally, we note that our modeling will be useful for studying the radio photospheres of some Mira variables such that, thanks to their proximity to us (e.g., the prototype of this type of stars, Omicron Ceti, which is at a distance almost four times closer than Orion I; Whitelock & Feast 2000), we expect to detect their sodium and potassium RRLs in much shorter observing times.
A.B.-R. acknowledges support from a DGAPA postdoctoral grant (year 2015) to UNAM. I.J.-S. acknowledges the financial support received from the STFC through an Ernest Rutherford Fellowship (proposal no. ST/L004801/2). J.M.-P. acknowledges partial support by the MINECO under grants FIS2012-39162-C06-01 and ESP2015-65597-C4-1 and Comunidad de Madrid grant no. S2013/ICE-2822 SpaceTec-CM. S.C. acknowledges support from DGAPA, UNAM, and CONACyT, Mexico. We are grateful to Mark Reid for providing us with his results of the electron temperature and density structure of radio photospheres of long-period variable stars.
Facility: SMA - SubMillimeter Array.
Software: MORELI (Báez-Rubio et al. 2013), MADCUBA (Rivilla et al. 2016), MIR,11 MIRIAD (Sault et al. 1995).
Appendix A: Radio Continuum Fluxes
In Table 5, we show the whole set, to our knowledge, of radio continuum fluxes available in the literature with θHPBW <1.5 arcsec.
Table 5. Compilation of the Continuum Fluxes Measured toward Orion I
| Frequency | Radio Continuum Flux | Synthesized Beam | Instrument | References |
|---|---|---|---|---|
| ν (GHz) | Sc (mJy) | θFWHM (mas × mas) | ||
| 8.328 | 1.2 ± 0.1 | 0.26 × 0.22 | VLA | Gómez et al. (2008) |
| 8.328 | 0.43 ± 0.04 | 0.32 × 0.24 | VLA | Zapata et al. (2004) |
| 8.328 | 0.45 ± 0.04 | 0.32 × 0.24 | VLA | Zapata et al. (2004) |
| 8.328 | 0.83 ± 0.07 | 0.32 × 0.24 | VLA | Zapata et al. (2004) |
| 8.328 | 0.87 ± 0.05 | 0.32 × 0.24 | VLA | Zapata et al. (2004) |
| 8.4 | 1.1 ± 0.2 | 0.22 × 0.22 | VLA | Menten & Reid (1995) |
| 15. | 1.54 ± 0.18 | 0.14 × 0.13 | VLA | Felli et al. (1993a) |
| 15. | 1.6 ± 0.4 | ∼0.30 | VLA | Felli et al. (1993b) |
| 22. | 5.7 ± 0.9 | 0.109 × 0.097 | VLA | Forbrich et al. (2008) |
| 30.5 | 7.3 ± 1.5 | 0.130 × 0.083 | VLA | Rivilla et al. (2015) |
| 33.6 | 9.2 ± 1.1 | 1.30 × 0.65 | VLA | Rivilla et al. (2015) |
| 33.6 | 9.1 ± 1.2 | 0.92 × 0.60 | VLA | Rivilla et al. (2015) |
| 33.6 | 12.5 ± 1.5 | 0.75 × 0.56 | VLA | Rivilla et al. (2015) |
| 33.6 | 10.7 ± 1.3 | 0.86 × 0.56 | VLA | Rivilla et al. (2015) |
| 33.6 | 10.8 ± 1.2 | 0.30 × 0.24 | VLA | Rivilla et al. (2015) |
| 33.6 | 9.7 ± 1.1 | 0.28 × 0.22 | VLA | Rivilla et al. (2015) |
| 33.6 | 9.3 ± 1.0 | 0.620 × 0.077 | VLA | Rivilla et al. (2015) |
| 33.6 | 10.8 ± 1.2 | 0.140 × 0.062 | VLA | Rivilla et al. (2015) |
| 33.6 | 8.1 ± 0.9 | 0.091 × 0.060 | VLA | Rivilla et al. (2015) |
| 37.5 | 9.1 ± 1.9 | 0.096 × 0.073 | VLA | Rivilla et al. (2015) |
| 42.8 | 14.5 ± 0.7 | 0.17 × 0.15 | VLA | Rodríguez et al. (2009) |
| 43 | 13 ± 2 | 0.25 × 0.25 | VLA | Menten & Reid (1995) |
| 43 | 13 ± 1.3 | 0.034 × 0.034 | VLA | Reid et al. (2007) |
| 43 | 14.5 ± 0.7 | 0.17 × 0.15 | VLA | Rodríguez et al. (2009) |
| 43 | 11 ± 2 | 0.06 × 0.04 | VLA | Goddi et al. (2011) |
| 45.6 | 14.1 ± 1.7 | 0.23 × 0.15 | VLA | Rivilla et al. (2015) |
| 45.6 | 12.5 ± 1.5 | 0.22 × 0.15 | VLA | Rivilla et al. (2015) |
| 86 | 34 ± 5 | 1.00 × 0.38 | BIMA | Plambeck et al. (1995) |
| 89 | 50 ± 5 | 0.40 × 0.35 | CARMA | Friedel & Widicus Weaver (2011) |
| 229 | 310 ± 45 | 0.15 × 0.13 | CARMA | Plambeck et al. (2013) |
| 229 | 330 ± 50 | 0.18 × 0.15 | ALMA | Plambeck & Wright (2016) |
| 245 | 272 ± 13 | 0.81 × 0.64 | ALMA | Hirota et al. (2015) |
| 339 | 849 ± 29 | 0.49 × 0.45 | ALMA | Hirota et al. (2015) |
| 341 | 1400 ± 100 | 0.80 × 0.70 | SMA | Tang et al. (2010) |
| 346.58 | 320 ± 48 | 0.78 × 0.65 | SMA | Beuther et al. (2004) |
| 349 | 816 ± 80 | 0.25 × 0.18 | ALMA | Plambeck & Wright (2016) |
| 353.6 | 430 ± 27 | 0.70 × 0.41 | SMA | Section 2 |
| 430 | 1338 ± 11 | 0.083 × 0.067 | ALMA | Hirota et al. (2016) |
| 460 | 1547 ± 14 | 0.104 × 0.087 | ALMA | Hirota et al. (2016) |
| 490 | 1709 ± 12 | 0.111 × 0.079 | ALMA | Hirota et al. (2016) |
| 661 | 3455 ± 520 | 0.160 × 0.120 | ALMA | Plambeck & Wright (2016) |
| 690 | 6700 ± 3200 | 1.4 × 0.9 | SMA | Beuther et al. (2006) |
Download table as: ASCIITypeset image
Appendix B: Spectroscopy of Metals at Radio Wavelengths
In principle, the spectroscopy of metal RRLs could be established with sophisticated treatments. However, as a first approximation, the frequencies of RRLs due to K and Na can be estimated under the hydrogenic approximation. This is justified because, in alkali metal, the recombined and excited outermost electron feels an effective nuclear charge approximately equal to 1, as for the hydrogen atom.
This approximation is especially appropriate to estimate submillimeter and millimeter RRLs (principal quantum numbers higher than 12) even for non-alkaline elements because the outermost electron, responsible for these lines when it gets de-excited, is very distant from the nucleus and the rest of the filled electron shells. Thus, the frequencies of metal RRLs can be derived with the Rydberg formula but taking into account a different nuclear mass given the higher atomic numbers of these elements, i.e.,
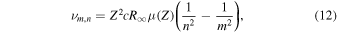
where n and m represent the lower and upper principal quantum numbers of the transition, respectively, c is the light speed,  is the Rydberg constant for an atom with assumed infinite nuclear mass, and
is the Rydberg constant for an atom with assumed infinite nuclear mass, and  is the reduced mass of the system formed by the atomic nucleus and the outermost electron, i.e.,
is the reduced mass of the system formed by the atomic nucleus and the outermost electron, i.e.,
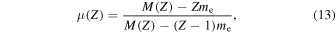
where  and me are the nuclear and electron masses, respectively.
and me are the nuclear and electron masses, respectively.
Thus, the metal RRL frequencies would be redshifted with respect to that of the hydrogen atom by an amount that depends on the reduced mass of that metal. Since the reduced mass of atomic elements with very high nuclear masses converges to 1, all the RRLs of heavy elements would arise at a similar frequency, shifted 163.3 km s−1 with respect to the same transition of the hydrogen atom. Fortunately, one can unambiguously identify RRLs of metals with low atomic numbers, such as the Na and K, with the shifts shown in Table 6.
Table 6. Atomic Weights and Shifting (in Units of Velocity) of the RRLs of the Most Abundant Elements with Respect to the Same Transition of the Hydrogen (1H) RRL
| Element | Atomic Number, Z | Nuclear Mass, 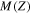 (uma) (uma) |
Δv (km s−1)a |
|---|---|---|---|
| 1H | 1 | 1.00782503207(10) | ... |
| 4He | 2 | 4.00260325415(6) | 122.16 |
| 12C | 6 | 12.0000000(0) | 149.56 |
| 23Na | 11 | 22.98976928(2) | 156.11 |
| 27Al | 13 | 26.9815385(7) | 157.17 |
| 39K | 19 | 38.96370649(3) | 159.05 |
| 40Ca | 20 | 39.9625909(2) | 159.15 |
Notes. The atomic weights have been taken from Meija et al. (2013) for the most abundant isotopes.
aΔv = c × Δμ.Download table as: ASCIITypeset image
Footnotes
- 5
The SubMillimeter Array is a joint project between the Smithsonian Astrophysical Observatory and the Academica Sinica Institute of Astronomy and Astrophysics and is funded by the Smithsonian Institution and the Academia Sinica.
- 6
Madrid Data Cube Analysis on ImageJ is a software developed at the Center of Astrobiology (Madrid, INTA-CSIC) to visualize and analyze single spectra and data cubes (see Rivilla et al. 2016).
- 7
The uncertainty has been estimated with a confidence interval of 95%.
- 8
NIST Atomic Spectra Database (ver. 5.2), available at http://physics.nist.gov/asd (2016 August 31). Kramida, A., Ralchenko, Yu., Reader, J., and NIST ASD Team (2014). National Institute of Standards and Technology, Gaithersburg, MD.
- 9
The H− is formed by two electrons bounded to a nucleus with a single proton with no bound excited electron states.
- 10
The velocity-integrated line-to-continuum ratios of the RRL are predicted to increase with frequency approximately as ν1.1 (Rodríguez et al. 2009) under LTE conditions and for optically thin regions.
- 11
The MIR-IDL cookbook by C. Qi can be found at https://www.cfa.harvard.edu/~cqi/mircook.html.







