Abstract
M dwarfs host most of the exoplanets in the local Milky Way. Some of these planets, ranging from sub-Earths to super-Jupiters, orbit in their stars' habitable zones (HZs), although many likely possess surface environments that preclude habitability. Moreover, exomoons around these planets could harbor life for long timescales and thus may also be targets for biosignature surveys. Here we investigate the potential habitability, stability, and detectability of exomoons around exoplanets orbiting M dwarfs. We first compile an updated list of known M-dwarf exoplanet hosts, comprising 109 stars and 205 planets. For each M dwarf, we compute and update precise luminosities with the Virtual Observatory spectral energy distribution Analyzer and Gaia DR2 parallaxes to determine inner and outer boundaries of their HZs. For each planet, we retrieve (or, when necessary, homogeneously estimate) their masses and radii, calculate the long-term dynamical stability of hypothetical moons, and identify those planets that can support habitable moons. We find that 33 exoplanet candidates are located in the HZs of their host stars and that four of them could host Moon- to Titan-mass exomoons for timescales longer than the Hubble time.
Export citation and abstract BibTeX RIS
1. Introduction
M dwarfs constitute only about one-third of the stellar mass of the Galaxy (Chabrier 2003), but about two-thirds of all its stars (Gould et al. 1996; Reid & Gizis 1997; Henry et al. 2006; Bochanski et al. 2010). Similar to their more massive stellar counterparts, M dwarfs also host exoplanets (Delfosse et al. 1998; Marcy et al. 1998; Butler et al. 2004; Bonfils et al. 2005, 2007, 2013a; Johnson et al. 2007; Udry et al. 2007; Dressing & Charbonneau 2015, among many others). Some of them orbit in the M-dwarf habitable zone (HZ), the circumstellar region where they can sustain liquid water on their surfaces (Hart 1979; Kasting et al. 1993; Scalo et al. 2007; Tarter et al. 2007; Ramírez 2018). The discoveries of such exoplanet candidates in temperate regions around their stars (e.g., Udry et al. 2007; Vogt et al. 2010, 2012; Anglada-Escudé et al. 2013, 2016; Tuomi et al. 2013; Dittmann et al. 2017; Gillon et al. 2017; Reiners et al. 2018) have come alongside theoretical calculations of HZs (Underwood et al. 2003; Selsis et al. 2007; Kopparapu et al. 2013; Zsom et al. 2013; Kopparapu et al. 2014; Barnes et al. 2015; Johns et al. 2018) and observational projects that aim to either discover Earth-like planets smaller than 1 M⊕ (e.g., Nutzman & Charbonneau 2008; Zechmeister et al. 2009; Bonfils et al. 2013a; Artigau et al. 2014; Quirrenbach et al. 2014; Ricker et al. 2015; Sullivan et al. 2015) or characterize their atmospheres (Wunderlich et al. 2019).
The M dwarfs' ubiquity and long main-sequence lifetime may favor their planets to host biological organisms (Segura et al. 2005; Loeb et al. 2016; Mullan & Bais 2018). However, given the low luminosities of M dwarfs (Delfosse et al. 2000; Reid & Hawley 2005; Benedict et al. 2016; Schweitzer et al. 2019), Earth-like planets in their HZs are located at short orbital separation to their stars, which enhances the probability to detect transits or induced radial velocity (RV) signals, translates into synchronous rotation, and consequently into tidal locking (Dole 1964; Peale 1977a, 1977b; Joshi et al. 1997; Murray & Dermott 1999; Tarter et al. 2007; Kite et al. 2011; Barnes 2017). This induced synchronous rotation has strong implications on the habitability of M-dwarf hosted planets because a hemisphere always faces the star and the other remains in complete darkness, introducing a spatially dependent incoming radiation and a temperature gradient between both hemispheres. Models of atmospheric circulation in dry, tidally locked, rocky exoplanets have shown that this circulation acts as a global engine that constrains large-scale wind speeds (Heng et al. 2011; Showman & Polvani 2011; Yang et al. 2013; Koll & Abbot 2016). Besides, in exoplanets that orbit close to their host stars, tidal interaction can affect climate stability, apart from spin and orbital properties (Kasting et al. 1993; Barnes et al. 2008; Heller et al. 2011a, 2011b; Shoji & Kurita 2014). In addition, flaring activity, which is frequent in M dwarfs (Jeffers et al. 2018; Loyd et al. 2018, and references therein), can cause strong atmospheric erosion in their exoplanets, with greater incidence on those that have no, or weak, magnetic moments (Buccino et al. 2006; Cnossen et al. 2007; Lammer et al. 2007; Segura et al. 2010; Vidotto et al. 2013; Shoji & Kurita 2014; France et al. 2018; Howard et al. 2018; Rodríguez et al. 2018). On the other hand, Driscoll & Barnes (2015) showed that core convection could still drive a strong geodynamo for gigayears on tidally locked worlds. Our knowledge of the atmospheres of Earth-like (and super-Earth) planets with one hemisphere under constant, strong irradiation is still incomplete, but the presence of a thick atmosphere or an ocean might help distribute the heat across the planet (Joshi et al. 1997; Joshi 2003; Scalo et al. 2007; Tarter et al. 2007; Selsis et al. 2011; Heng & Kopparla 2012; Showman & Kaspi 2013; Kopparapu et al. 2014; Yang et al. 2014; Wordsworth 2015; Turbet et al. 2016; Way et al. 2018, see also Pierrehumbert & Gaidos 2011 for H2-rich atmospheres).
One way to analyze the synchronous-rotation habitability problem of M-dwarf exoplanets is to introduce the presence of one or more hypothetical exomoons. Contrary to their host planets, exomoons would not become tidally locked to the star, but more likely to the planet itself (Hinkel & Kane 2013—see also Goldreich & Soter 1966 and Reynolds et al. 1987 for spin–orbit coupling of moons in our solar system). As a result, both exomoon hemispheres would receive the same amount of energy. The presence of an exomoon would also alleviate a second habitability problem: except for a few cases, the best characterized M-dwarf hosted exoplanets are super-Earths or mini-Neptunes with masses greater than 4–5 M⊕, which could be oceanic or gaseous worlds without any rocky surface, rather than Earth-like planets (Léger et al. 2004; Raymond et al. 2004; Lammer et al. 2009; Hill et al. 2018). In this picture, exomoons of about the mass of the Earth (with masses large enough to have a carbon–silicate cycle) would be habitable in the anthropocentric view, as opposed to their more massive planet hosts.
Exomoons could also have effects on the habitability of their host exoplanets. For instance, the Moon contributes to steady the Earth's obliquity, which might have allowed life to develop in stable conditions for a sufficiently long time (Laskar et al. 1993, 2004; Lourens et al. 2001; although see Armstrong et al. 2014; Deitrick et al. 2018). It is considered that moons are more stable and have longer lifetimes when the planet/moon systems are further from the parent star, the planets are heavier, or the parent stars are lighter (Barnes & O'Brien 2002; Sasaki et al. 2012; Sasaki & Barnes 2014). In addition to the flux received by the host star, a moon's climate and, thus, its habitability, can also be affected by planetary insolation and thermal emission, by periodic stellar eclipses, and by tidal heating (Zollinger et al. 2017). Tidal interactions between exoplanet and exomoon are a source of heating that is more relevant for the latter, such as in the inner Galilean moons (Yoder 1979; Peters & Turner 2013; Makarov & Efroimsky 2014; Clausen & Tilgner 2015; Tyler et al. 2015; Renaud & Henning 2018). Moderate tidal heating may help sustain tectonic activity, possibly a carbon–silicate cycle, and may also provide energy for biochemical reactions (Campanella 2009; Kaltenegger 2010; Heller 2012; Heller & Barnes 2013; Hinkel & Kane 2013; Heller et al. 2014; Forgan & Dobos 2016; Zollinger et al. 2017).
Exomoons are yet to be discovered (Kipping et al. 2013, 2015—but see the three Kepler candidates reported by Szabó et al. 2013, and especially Kepler-1625 b—Teachey et al. 2018; Teachey & Kipping 2018; Heller et al. 2019; Kreidberg et al. 2019). Most planet detection techniques are not applicable to that of exomoons due to the small relative sizes in comparison with their host planets. One of the most relevant techniques is the transits method, but it relies upon favorable geometric conditions and high photometric precision (Kipping et al. 2009, 2012). For the majority of exoplanet–exomoon phase curves, the lunar component is undetectable to the current technology of transits observations, and future surveys would require a photometric precision of a few parts per million (Forgan 2017, but see again Teachey & Kipping 2018). Nevertheless, the detectability of exomoons has been proposed feasible with current or near-future technology and a variety of methods: microlensing (Han & Han 2002), photocentric transit timing variation (Simon et al. 2007, 2015), modulation of planetary radio emissions (Noyola et al. 2014), spectroastrometry (Agol et al. 2015), polarization of transits (Berzosa Molina et al. 2018), radial velocity (Vanderburg et al. 2018), and transits of the plasma torus produced by a satellite (Ben-Jaffel & Ballester 2014; see the reviews by Cabrera & Schneider 2007; Perryman 2018, and Heller 2018). In particular, the European Space Agency (ESA) mission CHaraterising ExOPlanet Satellite (CHEOPS) could detect Earth-sized exomoons with the transit method (Simon et al. 2015).
Here, we explore the potential habitability of exomoons around known M-dwarf exoplanets. We compile a state-of-the-art list of M-dwarf exoplanetary systems, derive precise stellar luminosities from multiwavelength photometry and Gaia DR2 parallaxes, apply conservatively the radiative transfer equilibrium equation, identify exoplanets in HZ that can be orbited by exomoons, discuss their detectability, and investigate their long-term dynamical stability based on the latest models by Piro (2018), who modeled exoplanets torqued by the combined tides of an exomoon and a host star in order to find timescales for the gravitational loss/destruction of the exomoon.
2. Analysis
2.1. Stellar and Exoplanet Sample
As of 2019 March 19, the Extrasolar Planets Encyclopaedia6 had reported a total of 4011 exoplanets with the label "confirmed" (Schneider et al. 2011). In our analysis, first, we discarded the 258 planets detected by direct imaging (123), microlensing (88), pulsar timing (33), transit timing variation (8), and astrometry (6), many of which are located at large distances from the solar system and orbital separations, suffer from strong high-energy radiation, are difficult to characterize, or even are bona fide brown dwarfs (Caballero 2018).
Of the remaining 3734 planets, 205 orbit 109 systems with M-dwarf hosts detected via transit and/or radial velocity. To identify them, we selected all planets orbiting stars with M spectral type in the Extrasolar Planets Encyclopaedia except for nine giants and subgiants (HD 208527, HD 220074), pre-main-sequence stars (CVSO 30, V830 Tau), and spectroscopic, eclipsing, and close binaries (DW UMa, HD 41004 B, Kepler-64, KIC 5095269 AB, NLTT 41135). Besides, we selected all planets orbiting stars without spectral type in the Encyclopaedia, but with masses lower than 0.71 M⊙, which is the largest mass of an M dwarf in the Encyclopaedia, and that have M spectral type in the NASA Exoplanet Archive.7 Among the 205 exoplanets, we also included the planets orbiting the trio of stars BD–21 784, BD–06 1339, and Kepler-155 (Lo Curto et al. 2013; Rowe et al. 2014; Tuomi et al. 2014), which have been spectroscopically classified as stars at the K–M boundary (Upgren et al. 1972; Stephenson 1986; Zechmeister et al. 2009; Muirhead et al. 2012a; Gaidos et al. 2013; Tuomi et al. 2014), and LP 834-042 c, which is listed in the Encyclopaedia as detection_type=Other but has a radial velocity confirmation (Astudillo-Defru et al. 2017b).
The 109 M dwarfs and 205 exoplanets are listed in the Appendix tables. For the stars, we tabulate common/discovery and alternative names,8 equatorial coordinates and parallactic distances from Gaia DR2 (Gaia Collaboration et al. 2018), except for Luyten's star and Lalande 21185, for which we used Hipparcos parallactic distances (van Leeuwen 2007). Distances range from merely 1.30 pc (Proxima Centauri; Anglada-Escudé et al. 2016) to about 430 pc (Kepler-235; Borucki et al. 2011). All stars further than 30 pc have been discovered by Kepler (and K2) except for NGTS–1 and HATS–6 (Hartman et al. 2015; Bayliss et al. 2018). Besides, most of them are field M dwarfs, but at least four belong to stellar cluster members or associations (namely K2-25 in the Hyades–Mann et al. 2016a, K2-33 in Upper Scorpius–Mann et al. 2016b, K2-95 and K2-264 in the Praesepe–Pepper et al. 2017; Livingston et al. 2019).
For the planets, we tabulate their names, letters, main orbital parameters (semimajor axes a and orbital periods Porb), and corresponding references. For the 43 planets without a published semimajor axis (e.g., Rowe et al. 2014; Muirhead et al. 2015; Sahlmann et al. 2016), we derived them from their known periods and our estimated stellar masses, using Kepler's Third Law. For the 89 planets discovered with the RV method and without measured transits, we tabulate their minimum masses,  (marked with ">"), while for the 103 planets discovered with the transit method and without RV follow-up, we tabulate their radii. We have true masses and radii for 13 transiting planets with RV follow-up in 10 systems (see Table 1).
(marked with ">"), while for the 103 planets discovered with the transit method and without RV follow-up, we tabulate their radii. We have true masses and radii for 13 transiting planets with RV follow-up in 10 systems (see Table 1).
Table 1. Exoplanets with True Masses and Radii
| Star | Planet | Transit | RV |
|---|---|---|---|
| Referencesa | Referencesa | ||
| HATS-6 | b | Har15 | Har15 |
| PM J11302+0735 | b | Clo17 | Sar18 |
| Kepler 45 | b | Jon12 | Jon12 |
| LHS 1140 | b | Dit17 | Dit17 |
| c | Men19 | Men19 | |
| LHS 3275 | b | Har13 | Cha09 |
| LP 424–4 | b | Bon12 | Bon12 |
| LTT 3758 | b | Sou17 | Bon18 |
| PM J11293-0127 | b | Sin16 | Alm15 |
| c | Sin16 | Alm15 | |
| d | Sin16 | Alm15 | |
| Ross 905 | b | Mac14 | Tri18 |
| USco J161014.7-191909 | b | Man16b | Man16b |
Note.
aAlm15: Almenara et al. (2015); Bon12: Bonfils et al. (2012); Bon18b: Bonfils et al. (2018a); Cha09: Charbonneau et al. (2009); Clo17: Cloutier et al. (2017); Dit17: Dittmann et al. (2017); Har13: Harpsœet al. (2013); Har15: Hartman et al. (2015); Jon12: Johnson et al. (2012); Mac14: Maciejewski et al. (2014); Man16b: Mann et al. (2016b); Men19: Ment et al. (2019); Sar18: Sarkis et al. (2018); Sin16: Sinukoff et al. (2016); Sou17: Southworth et al. (2017); Tri18: Trifonov et al. (2018).Download table as: ASCIITypeset image
2.2. Planetary Masses and Radii
RV measurements only yield the minimum mass of an exoplanet, whereas transit measurements only yield the radius. For our habitability analysis, we used planet masses and radii. However, only 13 planets have both RV and transit measurements, i.e., true masses and radii (see above). As a result, for the other 192 planets, we derived planetary radii and masses. Among the multiple mass–radius relations available in the literature for different planetary compositions (e.g., Fortney et al. 2007; Seager et al. 2007; Sotin et al. 2007; Lissauer et al. 2011; Barnes et al. 2013; Wu & Lithwick 2013; Weiss & Marcy 2014; Barnes et al. 2015; Rogers 2015; Wolfgang et al. 2016; Chen & Kipping 2017; Kanodia et al. 2019), we chose that of Chen & Kipping (2017), as it covers a broad range of planetary sizes.
The largest planet transiting an M dwarf is NGTS–1 b, with R ∼ 1.33 RJup (Bayliss et al. 2018). On the other side of the relation, the smallest planets transit the stars Kepler 138 b, LSPM J1928+4437 (b, c, and d), Kepler-125 c, and 2MUCD 12171 (now universally known as TRAPPIST-1; d and h), and have masses and radii in the intervals 0.10–0.39 M⊕ and 0.52–0.78 R⊕, close to the values of Mars (0.107 M⊕, 0.343 R⊕). However, the distributions of masses and radii of the whole planet sample peak around 5–10 M⊕ and 1–3 R⊕, respectively.
2.3. Stellar Luminosities and Masses
First of all, we compiled Gaia DR2 equatorial coordinates (in J2015.5 epoch and J2000.0 equinox) with VizieR (Ochsenbein et al. 2000) for 107 of our stars. For the other two, Lalande 21185 and Luyten's star, without a Gaia DR2 entry, we retrieved the equatorial coordinates from Two Micron All Sky Survey (2MASS; Skrutskie et al. 2006), which were separated by less than two months from the J2000 epoch. Next, we collected multiband broadband photometry from the ultraviolet to the mid-infrared from the literature: GALEX DR5 (FUV, NUV; Bianchi et al. 2011), SDSS DR9 (ugri; Ahn et al. 2012), UCAC4 (BV, gri; Zacharias et al. 2013), Pan-STARRS1 DR1 (gri; Tonry et al. 2012; Chambers et al. 2016), Tycho-2 (BT, VT; Høg et al. 2000) APASS9 (BV, gri; Henden et al. 2016), 2MASS ( Skrutskie et al. 2006), Gaia DR2 (GBP G GRP; Gaia Collaboration et al. 2016, 2018), WISE (W1W2W3W4; Cutri et al. 2012), and allWISE (W1W2W3W4; Cutri et al. 2014).
Skrutskie et al. 2006), Gaia DR2 (GBP G GRP; Gaia Collaboration et al. 2016, 2018), WISE (W1W2W3W4; Cutri et al. 2012), and allWISE (W1W2W3W4; Cutri et al. 2014).
For that, we used the Upload X-Match tool of the interactive graphical viewer and editor for tabular data TOPCAT (Ochsenbein et al. 2000) with a search radius of 5'' and the "Best" find mode option. We made sure that the automatic cross-match was right by carrying out an inspection of each individual target and datum using the Aladin interactive sky atlas (Bonnarel et al. 2000), which provides simultaneous access to digitized images of the sky, astronomical catalogs, and databases. Eventually, for the 109 stars we compiled 1682 individual magnitudes along with their uncertainties.
We homogeneously derived the bolometric luminosity and effective temperature for each star with the compiled photometric data and the Virtual Observatory Spectral Energy Distribution Analyzer9 (VOSA; Bayo et al. 2008). We selected the best fit between a grid of BT-Settl-CIFIST theoretical spectral models (Baraffe et al. 2015) and our empirical data under the constraints log g = 4.5, 2000 K < Teff < 4500 K, and [Fe/H] = 0.0. The VOSA fits are acceptable in all cases, except for the extremely young star K2-33 in the Upper Scorpius association (David et al. 2016; Mann et al. 2016b; Schweitzer et al. 2019) and the metal-poor star K2-155 (Díez Alonso et al. 2018b; Hirano et al. 2018). Further details on the luminosity calculation will be described by C. Cifuentes et al. (2019, in preparation).
The luminosities of the 109 planet-host stars are displayed in the Appendix. As expected, the most luminous stars are at the K–M boundary, with L ∼ 0.14–0.17 L⊙. In particular, the most luminous stars, Kepler-155 and Kepler-252, have VOSA-derived Teff = 4300–4400 K, which are actually warmer than the hottest known M dwarfs (thus, their spectral types should be revised). On the other side, the least luminous stars, with L = (5–15) × 10−4 L⊙, are the latest and coolest ones, which in our case are 2MUCD 12171 and Proxima Centauri, which have M8.0 V and M5.5 V spectral types, respectively.
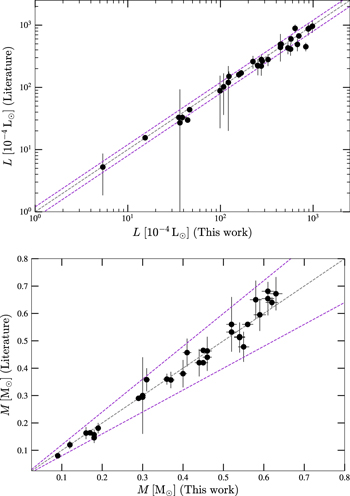
Finally, we computed stellar masses from Ks magnitude and distance using the relations of Mann et al. (2019). We display them in the last column of Table 5. The lowest masses, M* = 0.09–0.12 M⊙, are found again for 2MUCD 12171 and Proxima Centauri, and the highest ones, M* = 0.67–0.70 M⊙, correspond to the likely late-K dwarfs Kepler-155 and Kepler-252, K2-33 (actually incorrect, due to its extreme youth), and K2-155 (probably due to a metallicity effect). For comparison, we compiled published luminosities for 26 stars from the following works: Leggett et al. (2001), Howard et al. (2010), Boyajian et al. (2012), Gaidos & Mann (2014), Quintana et al. (2014), Hartman et al. (2015), Schlieder et al. (2016), Dittmann et al. (2017), Gillon et al. (2017), Maldonado et al. (2017), Bakos et al. (2018), Hirano et al. (2018), Ribas et al. (2018), Smith et al. (2018), Affer et al. (2019), Díez Alonso et al. (2019), Feinstein et al. (2019), Günther et al. (2019), Hobson et al. (2019), and Perger et al. (2019). The luminosities derived in this work are in good agreement with the values given in the literature (see Figure 1). Only five stars deviate more than 20% of the 1:1 ratio, but only one deviates significantly from our measurement. For BD–17 400, we calculated L = (835 ± 13) × 10−4 L⊙, but Leggett et al. (2001) tabulated L = (450 ± 70) × 10−4 L⊙ with pre-Gaia data. The other four stars have luminosities consistent within error bars with our measurements (LP 656–38,10 Leggett et al. 2001; GJ 96, Gaidos & Mann 2014; Kepler-186, Quintana et al. 2014; K2-149, Hirano et al. 2018).
Figure 1. Comparison between our luminosities (top) and masses (bottom) and those available in the literature. The dashed lines indicate the 1:1 ratio and 20% variations with respect to it.
Download figure:
Standard image High-resolution image3. Results and Discussion
3.1. Exoplanet Habitability
We calculated an HZ for each host star using the one-dimensional climate models from Kopparapu et al. (2014). We chose their "recent Venus" and "maximum greenhouse" estimates for the inner and outer HZ, respectively. The exoplanets' oceans might begin to evaporate and condense in the stratosphere at planetary equilibrium temperatures ≈320–340 K ("moist–greenhouse," Kasting et al. 1993; Kopparapu et al. 2013, 2014). However, between this process and the complete oceanic evaporation (runaway greenhouse limit, Kasting et al. 1993; Kopparapu et al. 2013, 2014), the exoplanets could still have surface temperatures adequate for habitability ("continuosly HZ," Hart 1978; Kasting et al. 1993).
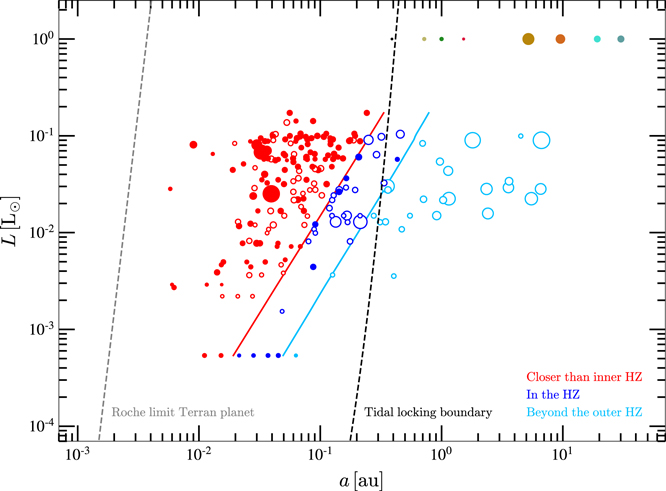
Figure 2 illustrates the HZ computation for our compiled exoplanet-host M dwarfs. The exoplanet candidates are depicted in three different colors, depending on whether they lie between their host stars and the inner HZ boundary (146), whether they lie between the inner and outer HZ boundary (33), or whether they lie beyond the outer HZ boundary (26). The 33 potentially habitable exoplanets are marked with the string "Yes" in column "Potentially HZ" from Table 6. Of the 33 planet candidates, 10 have masses or minimum masses above 10 M⊕ and 9 between 5 and 10 M⊕. Not counting the inclination angle effect in the RV planets, which translates into larger actual masses, most if not all of these 19 planets are mini-Neptunes and can hardly sustain liquid water on a rocky surface (Fortney et al. 2007; Miller-Ricci et al. 2009; Dorn et al. 2017). In other words, these 19 planets lie within the HZ of their stars, but they are unlikely to be habitable. However, their Earth-sized moons could actually be habitable.
Figure 2. Conservative HZ for all the M dwarfs in our sample (inner HZ, "recent Venus," in red; outer HZ, "maximum greenhouse," in sky blue). Their hosted exoplanets are depicted with sizes proportional to their masses in logarithmic scale, with filled circles if they have been detected by transit and with open circles if they have been detected by RV measurements. Exoplanets closer than the inner HZ, in the HZ, and beyond the outer HZ are shown in red, neon blue, and sky blue, respectively. The dashed, gray line is the Roche limit for an Earth-like planet (Aggarwal & Oberbeck 1974). The dashed, black line represents a "constant-time-lag" tidal locking model for a 10 M⊕-planet with rapid initial rotation after 1 Gyr (Barnes 2017). The eight solar system planets are depicted in the upper part of the plot.
Download figure:
Standard image High-resolution imageAs illustrated by Figure 2, three habitable planets are beyond the approximate 1 Gyr-tidal locking boundary: BD–06 1339 c (Lo Curto et al. 2013), Kepler-186 f (Torres et al. 2015), and HD 147379 b (Reiners et al. 2018). Of them, two are Neptune-like planets and one, Kepler-186 f, has a mass of only about 1.8 M⊕. However, following Barnes (2017), they will likely be tidally locked after 4.6 Gyr, the solar system age (see Section 3.2 for an individualized computation of planet locking times).
3.2. Exomoons around Potentially Habitable Exoplanets
We focused on the 33 exoplanets orbiting the HZ of their host stars and analyzed whether or not they could host exomoons on reasonable timescales. For that, we followed the work of Piro (2018), who considered null exomoon eccentricity and obliquity for simplicity. If an exoplanet hosting an exomoon is close enough to its host star, the star's gravity strips the exomoon away. This critical distance, namely the radius of the Hill sphere, is given by:
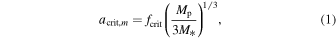
where Mp and M* are the exoplanet and star masses, and fcrit = 0.49, a critical factor that assumes a prograde orbit (Domingos et al. 2006; Piro 2018). Eventually, the exomoon will be stripped away by the host star if  , or fall back into the planet if
, or fall back into the planet if  , where am is the moon semimajor axis around the exoplanet.
, where am is the moon semimajor axis around the exoplanet.
If an exomoon gets too close to its host exoplanet, it will be tidally disrupted upon reaching the Roche limit, i.e., the point where the exomoon can no longer bind its material by gravitational forces. This condition is given by (Piro 2018):
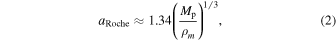
where ρm is the exomoon's density (see also Aggarwal & Oberbeck 1974). Under the assumption that all the initial angular momentum of an exoplanet eventually goes into its exomoon, the exomoon's semimajor axis can be written as:
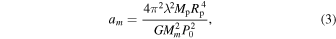
where λ (λ⊕ = 0.33, Williams 1994) is the exoplanet's radius of gyration ( , see Piro 2018), Mm is the exomoon mass, Ip is the planet moment of inertia, Rp is the planet radius, and P0 is the planet initial spin period. To estimate the exomoon migration timescale, namely, the e-folding timescale for the change in the exoplanet–exomoon distance, we used Equation (25) from Piro (2018), which can be rewritten as:
, see Piro 2018), Mm is the exomoon mass, Ip is the planet moment of inertia, Rp is the planet radius, and P0 is the planet initial spin period. To estimate the exomoon migration timescale, namely, the e-folding timescale for the change in the exoplanet–exomoon distance, we used Equation (25) from Piro (2018), which can be rewritten as:
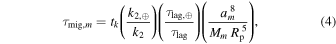
where tk = 250 Gyr, and am, Mm, and Rp are the exoplanet–exomoon separation, exomoon mass, and planetary radius in units of Earth–Moon separation, Moon mass, and Earth radius, respectively.11
Here, k2 is a Love number of degree 2 ( ) and τlag is the time lag between the passage of the perturber and the tidal bulge (Barnes 2017; Green et al. 2017; Piro 2018). For the Earth,
) and τlag is the time lag between the passage of the perturber and the tidal bulge (Barnes 2017; Green et al. 2017; Piro 2018). For the Earth,  (Lambeck 1977; Neron de Surgy & Laskar 1997). The time lag τlag is related with the tidal quality factor Q via (Henning et al. 2009; Matsumura et al. 2010; Barnes et al. 2013):
(Lambeck 1977; Neron de Surgy & Laskar 1997). The time lag τlag is related with the tidal quality factor Q via (Henning et al. 2009; Matsumura et al. 2010; Barnes et al. 2013):

where n is the mean motion, which implies that
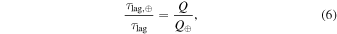
where Q⊕ = 12 (Williams et al. 1978). Therefore, combining Equations (3), (4) and (6),
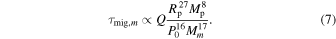
Table 2 summarizes the used values of k2, Q, and λ for four representative planetary types. These parameters are reasonable extrapolations of k2, Q, and λ from models of exoplanets and actual measurements of planets of different sizes and compositions (Dickey et al. 1994; Yoder 1995; Aksnes & Franklin 2001; Zhang & Hamilton 2006; Henning et al. 2009). For planets with sizes between Rp = 1.50 R⊕ (small, rocky worlds) and Rp = 3.88 R⊕ (Neptune), we fitted a linear function to k2:
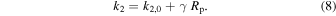
For Q and λ, we fitted, respectively, two power laws and two linear functions, between Rp = 1.50 R⊕ and Rp = 3.88 R⊕, and between Rp = 3.88 R⊕ and Rp = 10.97 R⊕ (Jupiter):
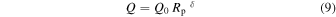
and
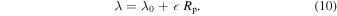
The values resulting from these fittings are listed in Table 3. Next, we computed the parameters aRoche, am, and  for the 33 exoplanets in HZ with a hypothetical exomoon. In our calculations, we set Mm = MMoon and ρm = 2500 kg m−3, which is a density intermediate between those of Io and Ganymede, but slightly lower than that of the Moon (that has a small iron core formed after the collision between Theia and the proto-Earth). The Roche limit, aRoche, smoothly depends on ρm (Equation (2)). For example, assuming the Earth density ρ⊕ = 5513 kg m−3, aRoche would only be increased by 23%. Next, we set
for the 33 exoplanets in HZ with a hypothetical exomoon. In our calculations, we set Mm = MMoon and ρm = 2500 kg m−3, which is a density intermediate between those of Io and Ganymede, but slightly lower than that of the Moon (that has a small iron core formed after the collision between Theia and the proto-Earth). The Roche limit, aRoche, smoothly depends on ρm (Equation (2)). For example, assuming the Earth density ρ⊕ = 5513 kg m−3, aRoche would only be increased by 23%. Next, we set  in Equation (4) when the exomoon is stripped (
in Equation (4) when the exomoon is stripped ( ) and used the value given by Equation (3) when it falls back (
) and used the value given by Equation (3) when it falls back ( ). We did not calculate
). We did not calculate  if am < aRoche. We remark that, for multiplanetary systems, these estimates may not be entirely accurate because of the impact of the other planets.
if am < aRoche. We remark that, for multiplanetary systems, these estimates may not be entirely accurate because of the impact of the other planets.
Table 2. Love Number, Tidal Quality Factor, and Radius of Gyration for Different Planetary Types
| Planet | k2 | Q | λ |
|---|---|---|---|
| Type | |||
| Dry telluric | 0.5 | 100 | 0.370 |
| Terran | 0.3 | 12 | 0.330 |
| Icy Neptunian | 1.5 | 104 | 0.230 |
| Gaseous Jovian | 1.5 | 106 | 0.254 |
Download table as: ASCIITypeset image
Table 3. Parameters for Deriving k2 (Equation (8)), Q (Equation (9)), and λ (Equation (10))
| Rp | k2,0 | γ | Q0 | δ | λ0 |  |
|---|---|---|---|---|---|---|
|
|
(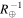 ) ) |
||||
| ≤1.50 | 0.3 | 0 | 102 | 0 | 0.37 | 0 |
| 1.50–3.88 | −0.456 | 0.504 | 14.019 | 4.846 | 0.458 | −0.059 |
| 3.88–10.97 | 1.5 | 0 | 24.600 | 4.431 | 0.217 | 0.003 |
| 10.97–26 | 1.5 | 0 | 106 | 0 | 0.254 | 0 |
Download table as: ASCIITypeset image
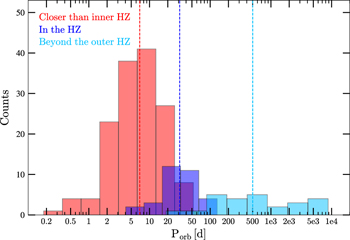
The initial planetary spin P0 is one of the greatest unknowns in such estimates. It is the orbital period, as opposed to the initial rotation period, which would be set by the last major impact. Figure 3 shows the orbital periods for all the exoplanets in our sample. Minimum and maximum Porb range from 4.3 hr (K2-137 b; Smith et al. 2018) to 24 yr (BD–05 5715 c; Montet et al. 2014), but they concentrate between 1 and 50 days. The range of Porb for the exoplanets in HZ is narrower, from 4 to 130 days, with a median value of 31 days. For completeness, the median Porb for inner and outer HZ planets are 7 days and 502 days, respectively.
Figure 3. Orbital periods for the exoplanets in our sample. The colors are the same as those in Figure 2. The dashed, vertical lines show the median period for each subgroup.
Download figure:
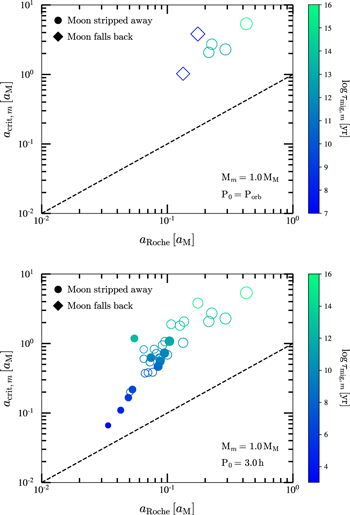
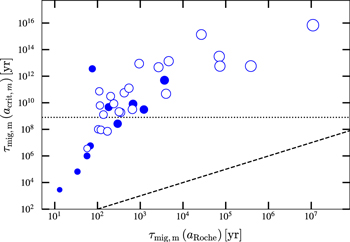
Standard image High-resolution imageFigure 4 depicts  versus aRoche for the 33 potentially habitable planets in our sample. It shows the two most extreme cases:
versus aRoche for the 33 potentially habitable planets in our sample. It shows the two most extreme cases:  and P0,2 = 3.0 hr. On the one hand, P0,1 = Porb (
and P0,2 = 3.0 hr. On the one hand, P0,1 = Porb ( ) is the longest allowed value of P0 because the exoplanet is tidally locked to its star. It is probably the most realistic case, as the habitable exoplanets in our sample orbit their stars under synchronous rotation. In particular, we computed the tidal locking time tlock with "constant-phase lag" (CPL, where the phase between the perturber and the tidal bulge is constant and insensitive to orbital and rotational frequencies) and "constant-time lag" (CTL, where the time interval between the perturber's passage and the tidal bulge is constant) models, using the publicly available EqTide12
code and the Proxima Centauri b system as a template (Barnes et al. 2016; Barnes 2017). We assumed zero eccentricity and obliquity, an initial planetary spin period of 3.0 h, a stellar Love number k2,* = 1.5, a stellar gyration radius λ* = 0.1 (λ⊙ = 0.061, Bouvier 2013), and the planetary parameters k2, Q, λ varying accordingly with Rp. We chose the minimum tlock between the calculations from the CPL and the CTL models.
) is the longest allowed value of P0 because the exoplanet is tidally locked to its star. It is probably the most realistic case, as the habitable exoplanets in our sample orbit their stars under synchronous rotation. In particular, we computed the tidal locking time tlock with "constant-phase lag" (CPL, where the phase between the perturber and the tidal bulge is constant and insensitive to orbital and rotational frequencies) and "constant-time lag" (CTL, where the time interval between the perturber's passage and the tidal bulge is constant) models, using the publicly available EqTide12
code and the Proxima Centauri b system as a template (Barnes et al. 2016; Barnes 2017). We assumed zero eccentricity and obliquity, an initial planetary spin period of 3.0 h, a stellar Love number k2,* = 1.5, a stellar gyration radius λ* = 0.1 (λ⊙ = 0.061, Bouvier 2013), and the planetary parameters k2, Q, λ varying accordingly with Rp. We chose the minimum tlock between the calculations from the CPL and the CTL models.
Figure 4.
 vs. aRoche for the modeled exomoons around all the potentially habitable exoplanets in our sample. The circles and the squares (filled for primary transit exoplanet detection, empty for RV exoplanet detection) represent an exomoon being stripped away by the host star or falling back into the exoplanet, respectively. They are depicted with sizes proportional to their exoplanet hosts' masses in logarithmic scale. The black, dashed line corresponds to the exomoon tidal disruption limit, so no exomoon can exist below it. Top: P0 = Porb for each planet. Bottom: P0 = 3.0 hr.
vs. aRoche for the modeled exomoons around all the potentially habitable exoplanets in our sample. The circles and the squares (filled for primary transit exoplanet detection, empty for RV exoplanet detection) represent an exomoon being stripped away by the host star or falling back into the exoplanet, respectively. They are depicted with sizes proportional to their exoplanet hosts' masses in logarithmic scale. The black, dashed line corresponds to the exomoon tidal disruption limit, so no exomoon can exist below it. Top: P0 = Porb for each planet. Bottom: P0 = 3.0 hr.
Download figure:
Standard image High-resolution imageWe found that only four habitable planets have tlock between 0.1 Gyr and 1 Gyr, namely LP 834–042 d (Astudillo-Defru et al. 2017b), PM J11293-0127 d (Almenara et al. 2015; Sinukoff et al. 2016), HD 156384 C e (Anglada-Escudé et al. 2013), and CD–44 11909 c (Tuomi et al. 2014), and 9 greater than 1 Gyr, GJ 96 b (Hobson et al. 2018), CD–23 1056 b (Forveille et al. 2011), BD–06 1339 c (Lo Curto et al. 2013), Ross 1003 b (Trifonov et al. 2018), HD 147379 b (Reiners et al. 2018), V1428 Aql b (Kaminski et al. 2018), Kepler-186 f (Torres et al. 2015), and IL Aqr b and c (Trifonov et al. 2018). In this situation, all of them could host exomoons beyond the Roche limit after all the material in the protoplanetary disk is dissipated (10–30 Myr, Bertout 1989; Hartmann et al. 1998; Calvet et al. 2002). All other habitable planets get tidally locked in less than 90 Myr.
However, the moon migration timescales are too low. In this scenario, only for six habitable exoplanets the condition am > aRoche holds. The migration timescales are greater than tH, being tH = 14.4 Gyr the Hubble time (which is slightly longer than the universe age at 13.8 Gyr), for four exoplanets (CD–23 1056 b, Forveille et al. 2011; Ross 1003 b, Haghighipour et al. 2010; Trifonov et al. 2018; IL Aqr b and c, Trifonov et al. 2018), whose properties are shown in the top part of Table 4 and discussed in Section 3.3. The four of them have  , the largest planetary radii in the HZ (Rp = 12–14 R⊕), and τmig ≫ 0.8 Gyr, which was the Earth's Late Heavy Bombardment duration (Fassett & Minton 2013; Norman & Nemchin 2014). In this P0,1 = Porb scenario, the hypothetical moons around the other 29 planets would fall onto them on timescales much shorter than protoplanetary disk dissipation times under the EqTide layout, not counting potential viscosity in the protomoon disk (Lin & Papaloizou 1986; Pollack et al. 1996; Montmerle et al. 2006; Sasaki et al. 2010). The fifth and sixth habitable exoplanets for which am > aRoche, LP 834–042 b and BD–06 1339 c, have short τmig of about 50 and 18 Myr, respectively, which are comparable to the typical protoplanetary disk dissipation time (Ida & Lin 2004; Hernández et al. 2007; Lambrechts & Johansen 2012).
, the largest planetary radii in the HZ (Rp = 12–14 R⊕), and τmig ≫ 0.8 Gyr, which was the Earth's Late Heavy Bombardment duration (Fassett & Minton 2013; Norman & Nemchin 2014). In this P0,1 = Porb scenario, the hypothetical moons around the other 29 planets would fall onto them on timescales much shorter than protoplanetary disk dissipation times under the EqTide layout, not counting potential viscosity in the protomoon disk (Lin & Papaloizou 1986; Pollack et al. 1996; Montmerle et al. 2006; Sasaki et al. 2010). The fifth and sixth habitable exoplanets for which am > aRoche, LP 834–042 b and BD–06 1339 c, have short τmig of about 50 and 18 Myr, respectively, which are comparable to the typical protoplanetary disk dissipation time (Ida & Lin 2004; Hernández et al. 2007; Lambrechts & Johansen 2012).
Table 4. Potentially Habitable Exoplanets That Can Host Exomoons
| Planet | GJ | a | Porb | M* | Mp | Rp | am | aRoche |

|
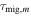
|
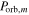
|
Qtidal |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (au) | (days) | (M⊙) | (M⊕) | (R⊕) | (aM) | (aM) | (aM) | (Gyr) | (days) | (TW) | ||
| CD-23 1056 b | ... | 0.25 | 53.435 | 0.62 | >114.0 | (>13.2) | 2.72 | 0.23 | 2.72 | >tH | ≤11.0 | ≲7 |
| Ross 1003 b | 1148 | 0.17 | 41.38 | 0.35 | >96.7 | (>12.0) | 2.08 | 0.21 | 2.08 | >tH | ≤8.0 | ≲32 |
| IL Aqr b | 876 | 0.21 | 61.082 | 0.34 | >760.9 | (>13.3) | 5.36 | 0.43 | 5.36 | >tH | ≤11.8 | ≲5 |
| IL Aqr c | 876 | 0.13 | 30.126 | 0.34 | >241.5 | (>14.0) | 2.29 | 0.29 | 2.29 | >tH | ≤5.9 | ≲126 |
Download table as: ASCIITypeset image
On the other hand, P0,2 = 3.0 hr ( ) is the smallest value used by Piro (2018), similar to the shortest Porb in our sample (P0,2 ≈ 4.13 hr, K2-137 b), which is close to its star and far from the HZ boundary, and probably near the shortest allowed value of P0 (see below). The value of 3.0 hr is also lower than the sidereal rotation periods of Jupiter and Saturn (9.925 and 10.55 hr, respectively), and might be unrealistic in the context of this work. Contrary to the P0,1 = Porb scenario, all moons are stripped away (which means that
) is the smallest value used by Piro (2018), similar to the shortest Porb in our sample (P0,2 ≈ 4.13 hr, K2-137 b), which is close to its star and far from the HZ boundary, and probably near the shortest allowed value of P0 (see below). The value of 3.0 hr is also lower than the sidereal rotation periods of Jupiter and Saturn (9.925 and 10.55 hr, respectively), and might be unrealistic in the context of this work. Contrary to the P0,1 = Porb scenario, all moons are stripped away (which means that  ), but with migration timescales greater than 0.8 Gyr for 26 planet–moon systems, including the four systems in Table 4. Of them, 15 planet–moon systems have τmig > tH. They are GJ 96 b (Hobson et al. 2018), CD–23 1056 b (Stassun et al. 2017), LP 834–042 b (Astudillo-Defru et al. 2017b), LP 834–042 d (Astudillo-Defru et al. 2017b), Kapteyn's star b (Anglada-Escudé et al. 2014), BD–06 1339 c (Lo Curto et al. 2013), PM J11293–0127 d (Almenara et al. 2015; Sinukoff et al. 2016), Ross 1003 b (Trifonov et al. 2018), HD 147379 b (Reiners et al. 2018), HD 156384 C e (Anglada-Escudé et al. 2013), CD–44 11909 c (Tuomi et al. 2014), V1428 Aql b (Kaminski et al. 2018), Kepler-186 f (Torres et al. 2015), and IL Aqr b and c (Trifonov et al. 2018). However, except for nine cases, GJ 96 b, CD–23 1056 b, BD–06 1339 c, Ross 1003 b, HD 147379 b, V1428 Aql b, Kepler-186 f, and IL Aqr b and c, all tidal locking times are shorter than 0.8 Gyr (
), but with migration timescales greater than 0.8 Gyr for 26 planet–moon systems, including the four systems in Table 4. Of them, 15 planet–moon systems have τmig > tH. They are GJ 96 b (Hobson et al. 2018), CD–23 1056 b (Stassun et al. 2017), LP 834–042 b (Astudillo-Defru et al. 2017b), LP 834–042 d (Astudillo-Defru et al. 2017b), Kapteyn's star b (Anglada-Escudé et al. 2014), BD–06 1339 c (Lo Curto et al. 2013), PM J11293–0127 d (Almenara et al. 2015; Sinukoff et al. 2016), Ross 1003 b (Trifonov et al. 2018), HD 147379 b (Reiners et al. 2018), HD 156384 C e (Anglada-Escudé et al. 2013), CD–44 11909 c (Tuomi et al. 2014), V1428 Aql b (Kaminski et al. 2018), Kepler-186 f (Torres et al. 2015), and IL Aqr b and c (Trifonov et al. 2018). However, except for nine cases, GJ 96 b, CD–23 1056 b, BD–06 1339 c, Ross 1003 b, HD 147379 b, V1428 Aql b, Kepler-186 f, and IL Aqr b and c, all tidal locking times are shorter than 0.8 Gyr ( ), which actually transforms this scenario into the previous one, P0,1 = Porb. For the four planets listed in Table 4, the migration timescales remain unscathed, as
), which actually transforms this scenario into the previous one, P0,1 = Porb. For the four planets listed in Table 4, the migration timescales remain unscathed, as  .
.
To better understand the values of the exomoon migration timescales, we calculated the maximum and minimum allowed  , i.e., we substituted
, i.e., we substituted  and am = aRoche in Equation (4), respectively. Figure 5 shows the range of
and am = aRoche in Equation (4), respectively. Figure 5 shows the range of  for the potentially habitable exoplanets in our sample. In principle, all the 24 exoplanets above the Earth's Late Heavy Bombardment line might host exomoons. However, the parameter space is only broad enough for the five exoplanets on the upper right side of Figure 5, which are the four planets listed in Table 4 and BD–06 1339 c. We compared our migration timescales for these five most extreme cases with the values resulting from applying the numerical technique of Piro (2018) by varying the planet–moon separation over an allowable range and the spin of the planet, and found that our values are slightly longer than, but comparable to, these. We kept our values for consistency.
for the potentially habitable exoplanets in our sample. In principle, all the 24 exoplanets above the Earth's Late Heavy Bombardment line might host exomoons. However, the parameter space is only broad enough for the five exoplanets on the upper right side of Figure 5, which are the four planets listed in Table 4 and BD–06 1339 c. We compared our migration timescales for these five most extreme cases with the values resulting from applying the numerical technique of Piro (2018) by varying the planet–moon separation over an allowable range and the spin of the planet, and found that our values are slightly longer than, but comparable to, these. We kept our values for consistency.
Figure 5. Maximum vs. minimum allowed values of exomoon migration timescales for the potentially habitable exoplanets in our sample. The points are depicted with sizes proportional to the exoplanets' masses in logarithmic scale. The black, dashed line corresponds to the most extreme case,  . The black, dotted, horizontal line shows the 0.8 Gyr boundary mentioned in the text (the Earth's Late Heavy Bombardment).
. The black, dotted, horizontal line shows the 0.8 Gyr boundary mentioned in the text (the Earth's Late Heavy Bombardment).
Download figure:
Standard image High-resolution image3.3. Potentially Habitable Exomoons
As presented in Section 3.2, only four potentially habitable exoplanets might be able to host exomoons for timescales above 0.8 Gyr under the P0 = Porb scenario: CD–23 1056b (a giant exoplanet around an active, metal-rich, M0.0 V star in Eridanus–Forveille et al. 2011), IL Aqr b,c (two giant exoplanets around a nearby M4.0 V star with a four-planet system—Delfosse et al. 1998; Marcy et al. 1998, 2001; Trifonov et al. 2018), and Ross 1003b (an eccentric, Saturn-mass planet around a nearby M4.0 V star with a multiplanetary system13 —Haghighipour et al. 2010; Trifonov et al. 2018). The four planets are relatively large and have minimum masses between 0.30 and 2.39 MJup (i.e., between 97 and 761 M⊕).
We analyzed the effects of tidal heating Qtidal (e.g., Barnes et al. 2008; Jackson et al. 2008a, 2008b, 2008c) on the four exomoons to assess if their mantles would melt, which, for a rocky body, occurs if Qtidal ≳ 100 TW (Moore et al. 2007; Lainey et al. 2009; Veeder et al. 2012; Driscoll & Barnes 2015). Barnes & Heller (2013) defined four categories of Earth-mass exoplanets in the HZ depending on the tidal heating that they experience: "Earth twins" (Qtidal < 20 TW), "Tidal Earths" (20 TW < Qtidal < 1020 TW), "Super-Ios" (1020 TW < Qtidal < 134000 TW), and "Tidal Venuses" (Qtidal > 134000 TW). We estimated Qtidal for each exoplanet–exomoon system by means of the publicly available VPLanet14
code (Barnes et al. 2016, 2018, 2019), modifying the example IoHeat. So far, we had assumed zero eccentricity and obliquity, as in Piro (2018), in which case tidal heating can only come from rotation, assuming that it is not synchronous. Hence, we relaxed this condition and set a small value for the eccentricity e = 0.01. We also assumed that the exomoon is tidally locked to the exoplanet. As Qtidal is directly proportional to the moon's size, we took a Ganymede-like exomoon to estimate an upper limit for the tidal heating (Ganymede is the biggest solar system moon).15
We set the exomoon's semimajor axis am to the mean distance between the Roche limit and the Hill radius from Table 4. We let each system evolve for t = 104 years and found that only a potential exomoon around IL Aqr c might reach the mantle melting threshold. We report the upper limit for  in Table 4.
in Table 4.
Some of these moons might be detected with current and near-future technology. The detectability of moons by the transit method (or, more likely, photocentric transit timing variation) has been extensively and intensively discussed in the literature (Sartoretti & Schneider 1999; Barnes & O'Brien 2002; Szabó et al. 2006; Pont et al. 2007; Kipping 2009; Kipping et al. 2014; Hippke & Angerhausen 2015; Simon et al. 2015; Perryman 2018). The ESA space mission (CHEOPS; Fortier et al. 2014) might discover moons with the transit method around the brightest M dwarfs, while, if the moons were massive and dense enough, ESPRESSO at the Very Large Telescope (Pepe et al. 2010) could also detect the modification of the amplitude and signature of the Rossiter–McLaughlin effect as in Zhuang et al. (2012). Unfortunately, none of the four planets in the stars' HZ with long moon migration times transits. If the NASA space mission TESS, currently in operation (Ricker et al. 2014), discovered additional M-dwarf planets in this class, but transiting, they should be a high priority target for ESPRESSO or any other ultra-stable spectrograph with cm s−1 accuracy at a large telescope.
Regarding the potential habitability of these Moon-mass exomoons, they may not retain an atmosphere at 300 K due to their low gravities. As Titan is less than twice as massive (1.83 MM), increasing the exomoon mass to Titan's would not significantly affect our results; the condition am > acrit,m for the four systems in Table 4 would still be met. The minimum mass to hold onto an atmosphere in the HZ of a star is not known, but is probably close to Mars' ( , Pollack et al. 1987; Selsis et al. 2007). If we increased the masses of our putative exomoons to Mars' mass, then, for the four systems in Table 4,
, Pollack et al. 1987; Selsis et al. 2007). If we increased the masses of our putative exomoons to Mars' mass, then, for the four systems in Table 4,  would be of the order of 5 million years for CD-23 1056b and Ross 1003b, and would lie above the Hubble time for IL Aqr b anc c. These four systems would remain near the upper right corner of Figure 5, indicating that their
would be of the order of 5 million years for CD-23 1056b and Ross 1003b, and would lie above the Hubble time for IL Aqr b anc c. These four systems would remain near the upper right corner of Figure 5, indicating that their  values are sufficiently long to still permit a long lifetime.
values are sufficiently long to still permit a long lifetime.
4. Conclusions
First of all, we compiled orbital, astrometric, photometric, and basic astrophysical parameters of a comprehensive list of 205 exoplanets around 109 M dwarfs discovered with the radial velocity or transit methods. We calculated the most probable masses and radii of 192 planets using the models of Chen & Kipping (2017), and assumed literature values for the other 13 planets with both radial velocity and transit measurements. For all 109 host stars, we derived luminosities, effective temperatures, and masses from public photometric catalogs, BT-Settl CIFIST models of the Lyon group, the Virtual Observatory Spectral energy distribution Analyzer, a near-infrared absolute magnitude-mass relation, and, except for only two cases, Gaia parallaxes.
With the available data, for every star we outlined the inner and outer HZ boundaries from a one-dimensional climate model. There are 33 known planets that orbit within the HZ limits of M dwarfs. Despite being tidally locked to their (active) host stars in most cases, it may still be possible for these planets to retain the conditions for habitability. In this scenario, even if most of the planets in the HZ might not host liquid water, because they are icy Neptunians, some of their hypothetical exomoons could instead.
For each of the 33 planets, we modeled noneccentric, nonobliquous moons, and computed moon migration timescales for two different scenarios: strip-away from the planet, and fall back onto the planet. We also considered two extreme cases for the initial planetary spin: a maximum value corresponding to the orbital period (i.e., the planet is tidally locked), and a minimum value of 3 hr. In the P0 = Porb scenario, all hypothetical moons fall back onto their planets after short timescales, except for four planets whose migration timescales are longer than the Hubble time (Ross 1003b, IL Aqr b and c, and CD–23 1056b). Only for these cases a hypothetical moon could be stable for timescales longer than protoplanetary disk dissipation times. We also explored the effects of tidal heating in the exomoons, in particular, if their mantles would partially melt, similar to Io in the solar system. All our code is publicly available in a GitHub repository16 and archived in Zenodo (doi.10.5281/zenodo.3533659).
Our planet compilation dates back to 2019 March 19. As a future work, a new M-dwarf exoplanet list should be updated with recent discoveries, such as Teegarden's b and c (Zechmeister et al. 2019) and, especially, the transiting warm Earth-mass planet GJ 357 b (Luque et al. 2019). Besides, the stellar mass determination could be improved with the new luminosity–radius–mass relation of Schweitzer et al. (2019) or, more interestingly, for studying the long-term stability of hypothetical moons, direct N-body analyses could be carried out.
H.M.-R. acknowledges support from a PITT PACC, a Zaccheus Daniel and a Kenneth P. Dietrich School of Arts & Sciences Predoctoral Fellowship from the Department of Physics and Astronomy at the University of Pittsburgh. J.A.C. and C.C. acknowledge financial support from the Agencia Estatal de Investigación of the Ministerio de Ciencia, Innovación y Universidades and the European FEDER/ERF funds through projects AYA2016-79425-C3-2-P, BES-2017-080769, and MDM-2017-0737. R.B. was supported by the NASA Virtual Planetary Laboratory Team through grant No. 80NSSC18K0829. This work also benefited from participation in the NASA Nexus for Exoplanet Systems Science research coordination network. This research has made use of NASA's Astrophysics Data System Bibliographic Services, the VizieR catalog access tool, VOSA, which is developed under the Spanish Virtual Observatory project supported from the Spanish MINECO through grant AYA2017-84089, and the NASA Exoplanet Archive, which is operated by the California Institute of Technology, under contract with the National Aeronautics and Space Administration under the Exoplanet Exploration Program.
Software: SciPy (Virtanen et al. 2019), Matplotlib (Hunter 2007), IPython (Pérez & Granger 2007), Numpy (Van Der Walt et al. 2011), Astropy (Astropy Collaboration et al. 2013; Price-Whelan et al. 2018), EqTide (Barnes et al. 2016; Barnes 2017), VPLanet (Barnes et al. 2016, 2018, 2019).
Appendix: Long Tables
Table 5 reproduces the basic properties of planet-host M dwarfs. Table 6 reproduces the basic properties of M-dwarf hosted exoplanets.
Table 5. Basic Properties of Planet-host M Dwarfs
| Name | Alternative | αa | δa | db | Sp. | Teffc | Lc | M*d |
|---|---|---|---|---|---|---|---|---|
| Names | (pc) | Type | (K) | (10−4 L⊙) | (M⊙) | |||
| GX And | GJ 15A | 00:18:27.04 | +44:01:29.0 | 3.563 ± 0.001 | M1.0 V | 3600 | 253.6 ± 4.0 | 0.40 |
| K2-149 | EPIC 220522664 | 00:39:17.22 | +07:16:37.2 | 124.1 ± 0.5 | M1 V | 3700 | 677 ± 17 | 0.59 |
| CD-44 170 | GJ 27.1 | 00:39:59.52 | −44:15:15.0 | 23.62 ± 0.03 | M0.5 V | 3700 | 459.7 ± 8.7 | 0.52 |
| LHS 1140 | GJ 3053 | 00:44:59.67 | −15:16:26.8 | 14.99 ± 0.02 | M4.5 V | 3100 | 44.25 ± 0.55 | 0.18 |
| 2MASS J01021226-6145216 | HATS-71 | 01:02:12.45 | −61:45:22.1 | 140.79 ± 0.86 | M3.0 V | 3300 | 251.9 ± 5.5 | 0.45 |
| BD+61 195 | GJ 49 | 01:02:40.50 | +62:20:43.6 | 9.856 ± 0.003 | M1.5 V | 3600 | 452.4 ± 9.5 | 0.54 |
| YZ Cet | GJ 54.1 | 01:12:31.94 | −16:59:46.5 | 3.712 ± 0.001 | M4.5 V | 3100 | 22.00 ± 0.35 | 0.14 |
| K2-150 | EPIC 220598331 | 01:13:22.65 | +08:59:14.8 | 102.8 ± 0.8 | M2.5 V | 3400 | 224.3 ± 5.5 | 0.41 |
| K2-151 | EPIC 220621087 | 01:17:13.15 | +09:30:04.6 | 69.6 ± 0.2 | M1.5 V | 3700 | 326.2 ± 4.6 | 0.46 |
| BD-17 400 | GJ 3138 | 02:09:11.46 | −16:20:21.3 | 28.49 ± 0.03 | M0 V | 3900 | 835 ± 13 | 0.61 |
| GJ 96 | G 173-53 | 02:22:14.98 | +47:52:48.8 | 11.936 ± 0.009 | M0 V | 3900 | 638.6 ± 9.4 | 0.58 |
| CD-23 1056 | LTT 1349 | 02:46:43.22 | −23:05:09.6 | 23.39 ± 0.02 | M0 V | 4000 | 908 ± 13 | 0.62 |
| LP 413-32 B | K2-288 B | 03:41:46.63 | +18:16:06.6 | 65.72 ± 0.87 | M3.0 V | 3200 | 364 ± 18 | 0.50 |
| BD-21 784 | GJ 160.2 | 04:06:34.90 | −20:51:23.3 | 25.88 ± 0.04 | K7 V | 4300 | 1372 ± 22 | 0.65 |
| LPM 178 | GJ 163 | 04:09:17.48 | −53:22:16.2 | 15.135 ± 0.007 | M3.5 V | 3400 | 217.0 ± 3.7 | 0.41 |
| Melotte 25 VA 50 | K2-25 | 04:13:05.74 | +15:14:51.7 | 45.0 ± 0.2 | M4.5 V | 3200 | 77.6 ± 1.3 | 0.27 |
| HG 8-15 | K2-155 | 04:21:52.48 | +21:21:12.9 | 73.0 ± 0.3 | M0.0 V | 3500 | 998 ± 15 | 0.66 |
| LP 834-042 | GJ 3293 | 04:28:35.63 | −25:10:16.8 | 20.20 ± 0.02 | M2.5 V | 3500 | 275.8 ± 3.9 | 0.45 |
| LEHPM 3808 | TOI-270 | 04:33:39.86 | −51:57:26.6 | 22.49 ± 0.01 | M3.0 V | 3500 | 167.6 ± 2.8 | 0.36 |
| LP 358-499 | K2-133 | 04:40:35.85 | +25:00:35.3 | 75.3 ± 0.2 | M1 V | 3800 | 351.3 ± 4.2 | 0.46 |
| HD 285968 | GJ 176 | 04:42:56.49 | +18:57:12.1 | 9.473 ± 0.006 | M2.0 V | 3500 | 364.8 ± 7.3 | 0.49 |
| Wolf 1539 | GJ 179 | 04:52:05.89 | +06:28:30.8 | 12.360 ± 0.009 | M3.5 V | 3300 | 157.6 ± 3.0 | 0.37 |
| LPM 198 | GJ 180 | 04:53:50.42 | −17:46:34.3 | 11.945 ± 0.004 | M2.0 V | 3500 | 242.7 ± 3.6 | 0.41 |
| LP 656-38 | GJ 3323 | 05:01:56.85 | −06:56:54.6 | 5.376 ± 0.002 | M4 V | 3100 | 36.54 ± 0.53 | 0.17 |
| Kapteyn's | GJ 191 | 05:11:50.08 | −45:02:34.9 | 3.9335 ± 0.0004 | M0 V | 3700 | 128.1 ± 3.5 | 0.38 |
| LP 892-26 | GJ 3341 | 05:15:47.31 | −31:17:41.4 | 23.64 ± 0.03 | M2.5 V | 3500 | 321.5 ± 5.1 | 0.47 |
| NGTS-1 | ... | 05:30:51.41 | −36:37:51.5 | 219.5 ± 1.0 | M0.5 V | 3900 | 679 ± 14 | 0.57 |
| HATS-6 | ... | 05:52:35.23 | −19:01:53.9 | 170.1 ± 1.1 | M1 V | 3800 | 702 ± 15 | 0.59 |
| BD-06 1339 | GJ 221 | 05:52:59.70 | −05:59:49.0 | 20.28 ± 0.02 | K7 V | 4100 | 1039 ± 24 | 0.63 |
| HD 42581 | GJ 229A | 06:10:34.46 | −21:52:03.8 | 5.757 ± 0.002 | M0.5 V | 3700 | 542 ± 28 | 0.55 |
| PM J06168+2435 | K2-26 | 06:16:49.54 | +24:35:45.0 | 99.3 ± 0.5 | M1 V | 3700 | 443.5 ± 9.0 | 0.52 |
| Luyten's star | GJ 273 | 07:27:25.09 | +05:12:35.6 | 3.80 ± 0.02 | M3.5 V | 3200 | 99.0 ± 3.5 | 0.29 |
| LP 424-4 | GJ 3470 | 07:59:05.64 | +15:23:28.4 | 29.45 ± 0.05 | M1.5 V | 3500 | 400.5 ± 4.9 | 0.50 |
| NGC 2632 JS 183 | K2-95 | 08:37:27.02 | +18:58:35.8 | 180.7 ± 4.0 | M3 V | 3400 | 219 ± 11 | 0.41 |
| K2-146 | EPIC 211924657 | 08:40:06.41 | +19:05:32.4 | 79.5 ± 0.5 | M3 V | 3300 | 123.6 ± 2.7 | 0.31 |
| LP 844-8 | GJ 317 | 08:40:58.69 | −23:27:10.1 | 15.203 ± 0.013 | M3.5 | 3300 | 224.1 ± 3.8 | 0.42 |
| NGC 2632 JS 597 | EPIC 211964830 | 08:45:26.00 | +19:41:54.2 | 186.6 ± 2.1 | M2 V | 3500 | 317.1 ± 9.5 | 0.47 |
| BD+02 2098 | GJ 328 | 08:55:07.67 | +01:32:31.2 | 20.54 ± 0.02 | M0.0 V | 3900 | 995 ± 12 | 0.63 |
| K2-117 | EPIC 211331236 | 08:55:25.38 | +10:28:09.2 | 101.9 ± 0.4 | M1.0 V | 3700 | 444.4 ± 9.4 | 0.52 |
| BD+48 1829 | GJ 378 | 10:02:20.77 | +48:04:56.8 | 14.96 ± 0.01 | M1.0 V | 3700 | 577 ± 10 | 0.56 |
| LTT 3758 | GJ 1132 | 10:14:50.18 | −47:09:17.8 | 12.618 ± 0.007 | M4.5 V | 3200 | 46.53 ± 0.58 | 0.19 |
| K2-239 | EPIC 248545986 | 10:42:22.59 | +04:26:28.9 | 31.11 ± 0.08 | M3.0 V | 3400 | 71.90 ± 0.94 | 0.23 |
| LP 905-36 | GJ 3634 | 10:58:34.40 | −31:08:39.6 | 20.39 ± 0.03 | M2.5 V | 3500 | 288.4 ± 4.5 | 0.46 |
| Lalande 21185 | GJ 411 | 11:03:20.19 | +35:58:11.6 | 2.547 ± 0.004 | M1.5 V | 3400 | 185 ± 13 | 0.41 |
| Innes' star | GJ 422 | 11:15:55.45 | −57:32:33.2 | 12.668 ± 0.007 | M3.5 V | 3400 | 179.0 ± 2.5 | 0.36 |
| K2-22 | EPIC 201637175 | 11:17:55.85 | +02:37:08.5 | 245.5 ± 2.8 | M0 V | 3900 | 810 ± 30 | 0.61 |
| PM J11293-0127 | K2-3 | 11:29:20.49 | −01:27:18.5 | 44.1 ± 0.1 | M0 V | 3900 | 603 ± 12 | 0.55 |
| PM J11302+0735 | K2-18 | 11:30:14.43 | +07:35:16.2 | 38.07 ± 0.08 | M2.5 V | 3500 | 264.0 ± 4.2 | 0.44 |
| CD-31 9113 | GJ 433 | 11:35:26.86 | −32:32:37.1 | 9.067 ± 0.004 | M1.5 V | 3600 | 339.5 ± 5.2 | 0.47 |
| Ross 1003 | GJ 1148 | 11:41:43.83 | +42:45:05.7 | 11.018 ± 0.006 | M4 V | 3200 | 149.9 ± 1.7 | 0.35 |
| Ross 905 | GJ 436 | 11:42:12.13 | +26:42:11.0 | 9.756 ± 0.009 | M2.5 V | 3300 | 238.9 ± 3.5 | 0.42 |
| LP 613-39 | K2-9 | 11:45:03.29 | +00:00:19.5 | 83.2 ± 0.4 | M2.5 V | 3500 | 121.7 ± 2.0 | 0.30 |
| FI Vir | GJ 447 | 11:47:45.02 | +00:47:57.4 | 3.375 ± 0.001 | M4 V | 3100 | 38.27 ± 0.56 | 0.18 |
| K2-152 | EPIC 201128338 | 12:06:31.78 | −05:49:38.8 | 108.8 ± 0.4 | M0 V | 3900 | 886 ± 16 | 0.61 |
| K2-153 | EPIC 201598502 | 12:15:14.13 | +02:01:15.2 | 143.7 ± 0.9 | M3.0 V | 3800 | 535 ± 12 | 0.54 |
| K2-137 | EPIC 228813918 | 12:27:28.90 | −06:11:42.8 | 99.2 ± 0.6 | M3 V | 3500 | 283.0 ± 6.1 | 0.46 |
| K2-154 | EPIC 228934525 | 12:36:00.36 | −02:40:10.6 | 129.8 ± 0.4 | M0 V | 3900 | 983 ± 16 | 0.63 |
| Ross 1020 | GJ 3779 | 13:22:56.05 | +24:27:50.2 | 13.749 ± 0.012 | M4.0 V | 3300 | 82.2 ± 1.0 | 0.25 |
| HD 122303 | GJ 536 | 14:01:02.33 | −02:39:08.2 | 10.412 ± 0.009 | M1 V | 3700 | 433.5 ± 7.2 | 0.51 |
| Proxima Centauri | GJ 551 | 14:29:34.43 | −62:40:34.3 | 1.3012 ± 0.0003 | M5.5 V | 2800 | 15.37 ± 0.39 | 0.12 |
| K2-240 | EPIC 249801827 | 15:11:23.85 | −17:52:31.6 | 73.1 ± 0.5 | M0.5 V | 3800 | 628 ± 15 | 0.57 |
| HO Lib | GJ 581 | 15:19:25.55 | −07:43:21.7 | 6.299 ± 0.002 | M3 V | 3400 | 120.0 ± 1.7 | 0.31 |
| K2-286 | EPIC 249889081 | 15:33:28.76 | −16:46:25.4 | 76.32 ± 0.23 | M0 V | 4000 | 904 ± 12 | 0.62 |
| MCC 759 | GJ 3942 | 16:09:03.49 | +52:56:38.9 | 16.937 ± 0.006 | M0 V | 3800 | 646.2 ± 7.3 | 0.57 |
| USco J161014.7-191909 | K2-33 | 16:10:14.73 | −19:19:09.8 | 139.8 ± 1.5 | M3 V | 3100 | 1019 ± 32 | 0.70 |
| LP 804-27 | HIP 79431 | 16:12:41.82 | −18:52:35.1 | 14.54 ± 0.03 | M3 V | 3400 | 301.8 ± 5.9 | 0.48 |
| HD 147379 | GJ 617A | 16:16:41.42 | +67:14:21.1 | 10.768 ± 0.004 | M0.0 V | 3900 | 978 ± 23 | 0.63 |
| MCC 767 | GJ 625 | 16:25:25.39 | +54:18:12.1 | 6.474 ± 0.001 | M2.0 V | 3500 | 148.1 ± 2.1 | 0.32 |
| V2306 Oph | GJ 628 | 16:30:17.96 | −12:40:03.7 | 4.306 ± 0.001 | M3.5 V | 3300 | 108.2 ± 1.6 | 0.30 |
| BD+25 3173 | GJ 649 | 16:58:08.72 | +25:44:31.1 | 10.383 ± 0.003 | M1.5 V | 3700 | 434.4 ± 4.6 | 0.52 |
| LHS 3275 | GJ 1214 | 17:15:19.54 | +04:57:38.4 | 14.65 ± 0.04 | M4.5 V | 3000 | 38.85 ± 0.50 | 0.18 |
| BD+11 3149 | GJ 3998 | 17:16:00.49 | +11:03:22.2 | 18.16 ± 0.02 | M1.0 V | 3700 | 467 ± 12 | 0.52 |
| HD 156384 C | GJ 667C | 17:19:00.25 | −34:59:52.0 | 7.245 ± 0.005 | M1.5 V | 3500 | 149.5 ± 2.3 | 0.33 |
| CD-46 11540 | GJ 674 | 17:28:40.81 | −46:53:56.3 | 4.550 ± 0.001 | M2.5 V | 3400 | 167.4 ± 3.0 | 0.35 |
| CD-51 10924 | GJ 676A | 17:30:10.77 | −51:38:16.0 | 16.035 ± 0.010 | M0 V | 3900 | 900 ± 16 | 0.63 |
| BD+68 946 | GJ 687 | 17:36:25.00 | +68:20:01.2 | 4.550 ± 0.001 | M3.0 V | 3400 | 221.1 ± 4.9 | 0.40 |
| CD-44 11909 | GJ 682 | 17:37:02.65 | −44:19:23.7 | 5.007 ± 0.002 | M3.5 V | 3200 | 81.18 ± 0.77 | 0.27 |
| BD+18 3421 | GJ 686 | 17:37:54.36 | +18:35:45.4 | 8.159 ± 0.002 | M1.5 V | 3700 | 277 ± 18 | 0.44 |
| Barnard's star | V2500 Oph | 17:57:48.49 | +04:41:40.5 | 1.827 ± 0.001 | M3.5 V | 3200 | 35.58 ± 0.72 | 0.16 |
| Kepler-83 | KOI-898 | 18:48:55.80 | +43:39:56.0 | 405.0 ± 5.2 | M0 V | 4100 | 919 ± 30 | 0.61 |
| Kepler-446 | KOI-2842 | 18:49:00.03 | +44:55:15.6 | 96.6 ± 0.5 | M4 V | 3400 | 49.74 ± 0.98 | 0.19 |
| Kepler-303 | KOI-1515 | 18:52:32.51 | +43:39:24.1 | 211.0 ± 0.9 | M0 V | 4100 | 876 ± 18 | 0.61 |
| Kepler-617 | KOI-596 | 18:54:57.77 | +47:30:58.1 | 174.2 ± 1.0 | M1 V | 3700 | 512.3 ± 9.2 | 0.55 |
| Kepler-236 | KOI-817 | 18:55:27.94 | +39:53:53.5 | 291.2 ± 2.3 | M1 V | 3900 | 755 ± 18 | 0.60 |
| Kepler-235 | KOI-812 | 19:04:18.98 | +39:16:41.7 | 433.2 ± 6.7 | M0 V | 4100 | 880 ± 34 | 0.61 |
| Kepler-52 | KOI-775 | 19:06:57.12 | +49:58:32.7 | 324.5 ± 2.4 | M0 V | 4200 | 1053 ± 25 | 0.63 |
| Kepler-155 | KOI-438 | 19:13:58.99 | +51:04:54.9 | 296.0 ± 2.3 | K7 V | 4400 | 1726 ± 58 | 0.68 |
| V1428 Aql | GJ 752A | 19:16:54.66 | +05:09:47.4 | 5.912 ± 0.002 | M2.5 V | 3500 | 325.8 ± 4.0 | 0.47 |
| Kepler-138 | KOI-314 | 19:21:31.54 | +43:17:35.0 | 67.0 ± 0.1 | M1 V | 3900 | 575.7 ± 7.5 | 0.54 |
| LSPM J1928+4437 | Kepler-42 | 19:28:52.70 | +44:37:02.5 | 40.11 ± 0.06 | M4 V | 3400 | 29.01 ± 0.36 | 0.14 |
| Kepler-49 | KOI-248 | 19:29:10.68 | +40:35:30.5 | 314.0 ± 2.5 | M1 V | 4000 | 946 ± 23 | 0.62 |
| LSPM J1930+4149 | Kepler-1649 | 19:30:00.71 | +41:49:48.0 | 92.4 ± 0.5 | M4: V | 3300 | 52.4 ± 1.0 | 0.20 |
| Kepler-45 | KOI-254 | 19:31:29.50 | +41:03:51.0 | 386.0 ± 6.5 | M1 V | 3800 | 807 ± 34 | 0.61 |
| Kepler-231 | KOI-784 | 19:35:53.61 | +50:31:54.7 | 319.5 ± 3.3 | M1 V | 4100 | 818 ± 26 | 0.59 |
| Kepler-54 | KOI-886 | 19:39:05.74 | +43:03:22.3 | 273.8 ± 2.9 | M1 V | 3800 | 480 ± 14 | 0.53 |
| Kepler-252 | KOI-912 | 19:42:19.04 | +44:32:45.3 | 383.6 ± 3.5 | M0 V | 4300 | 1421 ± 42 | 0.67 |
| Kepler-32 | KOI-952 | 19:51:22.15 | +46:34:27.7 | 326.9 ± 3.4 | M1 V | 3900 | 650 ± 19 | 0.57 |
| Kepler-125 | KOI-251 | 19:53:01.95 | +47:36:18.0 | 184.3 ± 1.0 | M1 V | 3800 | 558.7 ± 9.6 | 0.55 |
| Kepler-186 | KOI-571 | 19:54:36.66 | +43:57:18.0 | 178.5 ± 0.8 | M1 V | 3900 | 571 ± 14 | 0.55 |
| Kepler-445 | KOI-2704 | 19:54:56.72 | +46:29:56.8 | 127.7 ± 1.0 | M4 V | 3200 | 77.6 ± 2.1 | 0.28 |
| Kepler-267 | KOI-1078 | 19:59:19.34 | +47:09:27.3 | 267.0 ± 2.5 | M1 V | 3900 | 584 ± 16 | 0.55 |
| HD 204961 | GJ 832 | 21:33:33.90 | −49:00:45.1 | 4.965 ± 0.001 | M1.5 V | 3600 | 292 ± 11 | 0.44 |
| BD-05 5715 | GJ 849 | 22:09:41.52 | −04:38:27.0 | 8.803 ± 0.004 | M3.5 V | 3400 | 282.5 ± 4.2 | 0.47 |
| LP 819-052 | GJ 1265 | 22:13:43.79 | −17:41:13.4 | 10.255 ± 0.007 | M4.5 V | 3100 | 36.35 ± 0.46 | 0.17 |
| LP 700-6 | K2-28 | 22:22:29.60 | −07:57:22.9 | 63.1 ± 0.3 | M4 V | 3200 | 116.8 ± 2.3 | 0.33 |
| K2-21 | EPIC 206011691 | 22:41:12.91 | −14:29:21.6 | 83.8 ± 0.3 | M0 V | 4100 | 978 ± 14 | 0.63 |
| LHS 3844e | LEHPM 5027 | 22:41:59.09 | −69:10:19.6 | 14.891 ± 0.011 | m4: | 3000 | 27.10 ± 0.29 | 0.16 |
| IL Aqr | GJ 876 | 22:53:17.75 | −14:15:59.7 | 4.676 ± 0.002 | M4.0 V | 3200 | 129.3 ± 3.0 | 0.34 |
| 2MUCD 12171 | TRAPPIST-1 | 23:06:30.33 | −05:02:36.5 | 12.43 ± 0.02 | M8.0 V | 2500 | 5.38 ± 0.06 | 0.09 |
Notes.
aAll equatorial coordinates are given in the epoch of Gaia DR2 (J2015.5) (Gaia Collaboration et al. 2016), except for Luyten's star and Lalande 21185, with equatorial coordinates given in the epoch of 2MASS (J2000) (Skrutskie et al. 2006). bAll distances calculated using parallaxes from Gaia DR2 (Gaia Collaboration et al. 2016, 2018), except for Luyten's star and Lalande 21185, calculated using parallaxes from Hipparcos (van Leeuwen 2007). cL and Teff computed with VOSA (Bayo et al. 2008) from our compiled photometry. The uncertainties in the effective temperatures are δTeff = 50 K in all cases. dStellar masses calculated from Ks apparent magnitudes, tabulated distances, and the relations of Mann et al. (2019), as in Schweitzer et al. (2019). eSpectral type of LHS 3844 estimated from its photometric data.A machine-readable version of the table is available.
Table 6. Basic Properties of M-dwarf Hosted Exoplanets
| Name | Planet | a | Porb | Mpa | Rpa | Referencesb | Seff | Teq,p | Potentially |
|---|---|---|---|---|---|---|---|---|---|
| (au) | (days) | (M
|
(R⊕) | (S⊙) | (K) | HZ | |||
| GX And | b |
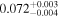
|
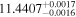
|
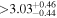
|
(>1.53) | Pin18 | 4.89 ± 0.10 | 413.9 ± 8.7 | ⋯ |
| K2-149 | b |
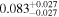
|
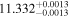
|
(3.85) |

|
Hir18 | 9.82 ± 0.25 | 493 ± 13 | ⋯ |
| CD-44 170 | b |
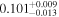
|

|
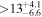
|
(>3.63) | Tuo14 | 4.51 ± 0.35 | 406 ± 32 | ⋯ |
| LHS 1140 | b |
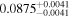
|
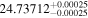
|
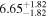
|
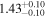
|
Dit17 | 0.5780 ± 0.0072 | 242.7 ± 3.0 | Yes |
| c |
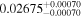
|

|
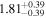
|
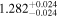
|
Men19 | 6.184 ± 0.077 | 438.9 ± 5.4 | ⋯ | |
| 2MASS J01021226-6145216 | b |
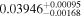
|
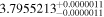
|
(1750) |

|
Bak18 | 16.18 ± 1.14 | 558 ± 39 | ⋯ |
| BD+61 195 | b |
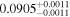
|
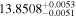
|
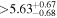
|
(>2.25) | Per19 | 5.52 ± 0.12 | 426.7 ± 9.0 | ⋯ |
| YZ Cet | b |
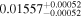
|
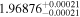
|
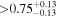
|
(>0.93) | Ast17a | 9.08 ± 0.14 | 483.1 ± 7.6 | ⋯ |
| c |
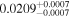
|

|

|
(>1.00) | Ast17a | 5.037 ± 0.079 | 417.0 ± 6.5 | ⋯ | |
| d |
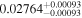
|
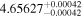
|
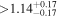
|
(>1.05) | Ast17a | 2.880 ± 0.045 | 362.6 ± 5.7 | ⋯ | |
| K2-150 | b |
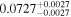
|
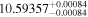
|
(5.26) |
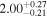
|
Hir18 | 4.24 ± 0.10 | 399.5 ± 9.8 | ⋯ |
| K2-151 | b |
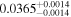
|
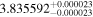
|
(2.44) |

|
Hir18 | 24.48 ± 0.34 | 619.1 ± 8.7 | ⋯ |
| BD-17 400 | b |
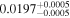
|
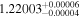
|
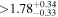
|
(>1.20) | Ast17b | 215.2 ± 3.4 | 1066 ± 17 | ⋯ |
| c |
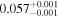
|
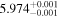
|
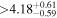
|
(>1.88) | Ast17b | 25.70 ± 0.41 | 626.7 ± 9.9 | ⋯ | |
| d |
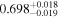
|
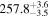
|
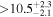
|
(>3.21) | Ast17b | 0.1714 ± 0.0027 | 179.1 ± 2.8 | ⋯ | |
| GJ 96 | b |
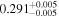
|

|
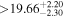
|
(>4.74) | Hob18 | 0.754 ± 0.011 | 259.4 ± 3.8 | Yes |
| CD-23 1056 | b |
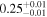
|
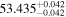
|
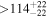
|
(>13.1) | Sta17 | 1.45 ± 0.12 | 306 ± 25 | Yes |
| LP 413-32 B | b |
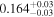
|

|
(4.01) |
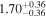
|
Fei19 | 1.354 ± 0.066 | 300 ± 15 | Yes |
| BD-21 784 | b |
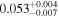
|

|
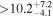
|
(>3.10) | Tuo14 | 48.8 ± 2.9 | 736 ± 43 | ⋯ |
| LPM 178 | b |
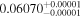
|
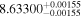
|
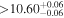
|
(>3.29) | Bon13b | 5.89 ± 0.10 | 433.6 ± 7.5 | ⋯ |
| c |
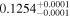
|
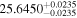
|
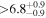
|
(>2.52) | Bon13b | 1.380 ± 0.024 | 301.6 ± 5.2 | Yes | |
| d |
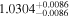
|
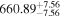
|
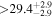
|
(>5.91) | Bon13b | 0.02044 ± 0.00035 | 105.2 ± 1.8 | ⋯ | |
| Melotte 25 VA 50 | b |
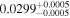
|
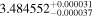
|
(11.6) |
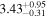
|
Man16a | 8.68 ± 0.15 | 477.7 ± 8.1 | ⋯ |
| HG 8-15 | b |
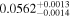
|

|
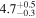
|
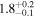
|
Die18 | 31.61 ± 0.49 | 660 ± 10 | ⋯ |
| c |
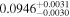
|
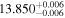
|
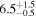
|
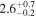
|
Die18 | 11.16 ± 0.17 | 509 ± 7.8 | ⋯ | |
| d |
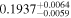
|
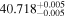
|
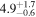
|
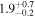
|
Die18 | 22.661 ± 0.041 | 355.5 ± 5.5 | ⋯ | |
| LP 834-042 | b |
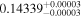
|
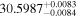
|
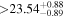
|
(>5.14) | Ast17b | 1.341 ± 0.019 | 299.5 ± 4.2 | Yes |
| c |
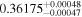
|

|
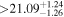
|
(>4.88) | Ast17b | 0.2108 ± 0.0030 | 188.6 ± 2.7 | ⋯ | |
| d |
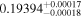
|
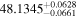
|
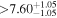
|
(>2.63) | Ast17b | 0.733 ± 0.010 | 257.5 ± 3.7 | Yes | |
| e |

|
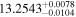
|

|
(>1.62) | Ast17b | 4.094 ± 0.058 | 395.9 ± 5.6 | ⋯ | |
| LEHPM 3808 | b |
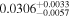
|
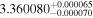
|
(1.98) |
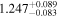
|
Gun19 | 17.89 ± 1.44 | 572 ± 46 | ⋯ |
| c |
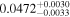
|
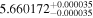
|
(6.88) |
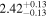
|
Gun19 | 7.52 ± 0.14 | 460.9 ± 8.3 | ⋯ | |
| d |
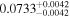
|
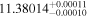
|
(5.48) |
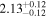
|
Gun19 | 3.119 ± 0.052 | 369.9 ± 6.2 | ⋯ | |
| LP 358-499 | b |
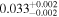
|
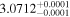
|
(2.29) |
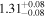
|
Wel17 | 32.26 ± 0.39 | 663.3 ± 8.0 | ⋯ |
| c |
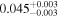
|
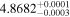
|
(3.07) |
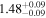
|
Wel17 | 17.35 ± 0.21 | 568.0 ± 6.8 | ⋯ | |
| d |
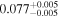
|
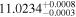
|
(5.15) |
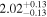
|
Wel17 | 5.925 ± 0.071 | 434.2 ± 5.2 | ⋯ | |
| HD 285968 | b |
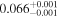
|
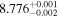
|
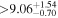
|
(>2.87) | Tri18 | 8.37 ± 0.17 | 473.5 ± 9.5 | ⋯ |
| Wolf 1539 | b |
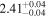
|
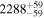
|

|
(>13.9) | How10 | 0.002714 ± 0.000052 | 63.5 ± 1.2 | ⋯ |
| LPM 198 | b |
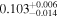
|
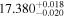
|
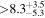
|
(>2.81) | Tuo14 | 2.29 ± 0.18 | 342.3 ± 27.1 | Yes |
| c |
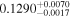
|
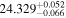
|
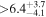
|
(>2.43) | Tuo14 | 1.459 ± 0.064 | 306 ± 13 | ⋯ | |
| LP 656-38 | b |
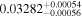
|
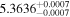
|
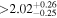
|
(>1.23) | Ast17b | 3.392 ± 0.049 | 377.7 ± 5.5 | ⋯ |
| c |
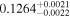
|
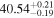
|
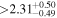
|
(>1.32) | Ast17b | 0.2287 ± 0.0033 | 192.5 ± 2.8 | ⋯ | |
| Kapteyn's | b |
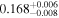
|

|
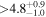
|
(>1.98) | Ang14 | 0.454 ± 0.014 | 228.4 ± 6.9 | Yes |
| c |
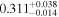
|
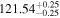
|
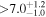
|
(>2.54) | Ang14 | 0.132 ± 0.012 | 167.9 ± 13.8 | ⋯ | |
| LP 892-26 | b | 0.089 |
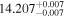
|
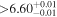
|
(>2.43) | Ast15 | 4.1 | 395 | ⋯ |
| NGTS-1 | b |
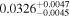
|
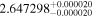
|

|
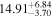
|
Bay18 | 63.9 ± 1.4 | 786.8 ± 16.9 | ⋯ |
| HATS-6 | b |
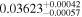
|
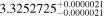
|
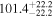
|
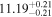
|
Har15 | 53.5 ± 1.2 | 752.7 ± 16.8 | ⋯ |
| BD-06 1339 | b |
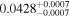
|
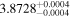
|
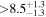
|
(>2.81) | LoC13 | 56.7 ± 1.3 | 763.9 ± 17.8 | ⋯ |
| c |
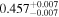
|
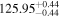
|
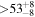
|
(>8.42) | LoC13 | 0.498 ± 0.012 | 233.8 ± 5.4 | Yes | |
| HD 42581 | b |
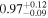
|
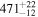
|
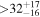
|
(>6.21) | Tuo14 | 0.0576 ± 0.0035 | 136.3 ± 8.3 | ⋯ |
| PM J06168+2435 | b |
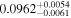
|
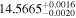
|
(7.64) |

|
Sch16 | 4.79 ± 0.10 | 411.8 ± 8.9 | ⋯ |
| Luyten's star | b |
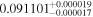
|

|
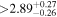
|
(>1.45) | Ast17b | 1.193 ± 0.042 | 291 ± 10 | Yes |
| c |
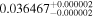
|
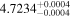
|
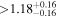
|
(>1.06) | Ast17b | 7.44 ± 0.26 | 460 ± 16 | ⋯ | |
| LP 424-4 | b |
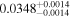
|
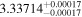
|

|
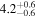
|
Bon12 | 33.07 ± 0.41 | 667.4 ± 8.2 | ⋯ |
| NGC 2632 JS 183 | b |
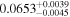
|
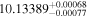
|
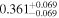
|
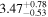
|
Obe16 | 5.13 ± 0.27 | 419 ± 22 | ⋯ |
| K2-146 | b |
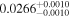
|
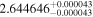
|
(5.48) |
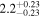
|
Hir18 | 17.47 ± 0.38 | 569 ± 13 | ⋯ |
| LP 844-8 | b |
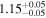
|
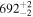
|
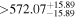
|
(>13.3) | Ang12 | 0.01695 ± 0.00029 | 100.4 ± 8.9 | ⋯ |
| c | 5.5 |
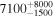
|
509 | (>13.5) | Ang12 | 0.00074 | 46 | ⋯ | |
| NGC 2632 JS 597 | b |
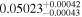
|
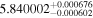
|
(5.83) |

|
Liv19 | 12.57 ± 0.38 | 524 ± 16 | ⋯ |
| c |
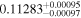
|
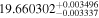
|
(7.64) |
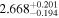
|
Liv19 | 2.490 ± 0.075 | 350 ± 11 | ⋯ | |
| BD+02 2098 | b |
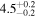
|
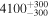
|
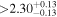
|
(>1.32) | Rob13 | 0.004911 ± 0.000060 | 73.68 ± 0.90 | ⋯ |
| K2-117 | b |
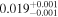
|
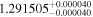
|
(4.84) |
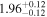
|
Dre17 | 123.1 ± 2.6 | 927 ± 20 | ⋯ |
| c |
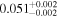
|
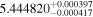
|
(5.26) |
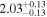
|
Dre17 | 17.09 ± 0.36 | 565 ± 12 | ⋯ | |
| BD+48 1829 | b |

|
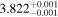
|
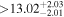
|
(>3.62) | Hob19 | 37.08 ± 0.67 | 687 ± 13 | ⋯ |
| LTT 3758 | b |
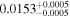
|
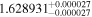
|
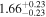
|

|
Sou17, Bon18b | 19.88 ± 0.25 | 587.7 ± 7.3 | ⋯ |
| c |
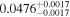
|
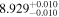
|
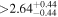
|
(>1.40) | Bon18b | 2.054 ± 0.026 | 333.2 ± 4.2 | ⋯ | |
| K2-239 | b |

|
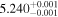
|
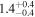
|

|
Die18 | 3.697 ± 0.048 | 385.9 ± 5.0 | ⋯ |
| c |
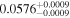
|
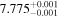
|

|
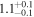
|
Die18 | 2.167 ± 0.026 | 337.7 ± 4.4 | ⋯ | |
| d |
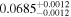
|

|
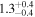
|
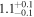
|
Die18 | 1.532 ± 0.048 | 309.7 ± 4.0 | ⋯ | |
| LP 905-36 | b |
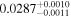
|
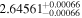
|
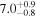 c
c
|
(>2.54) | Bon11 | 35.02 ± 0.56 | 677.0 ± 10.7 | ⋯ |
| Lalande 21185 | b | 0.0695 |
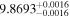
|
3.8 | (>1.75) | But17 | 3.84 ± 0.27 | 390 ± 27 | ⋯ |
| Innes' star | b |
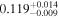
|
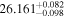
|
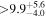
|
(>3.13) | Tuo14 | 1.264 ± 0.056 | 295 ± 13 | Yes |
| K2-22 | b | 0.009 |
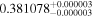
|
(20.2) |
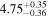
|
Dre17 | 1000 | 1565 | ⋯ |
| PM J11293-0127 | b |
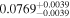
|
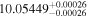
|
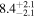
|
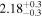
|
Alm15, Sin16 | 10.20 ± 0.20 | 497.4 ± 9.9 | ⋯ |
| c |
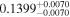
|

|
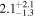
|
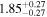
|
Alm15, Sin16 | 3.083 ± 0.062 | 368.8 ± 7.4 | ⋯ | |
| d |
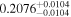
|
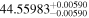
|
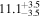
|
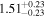
|
Alm15, Sin16 | 1.400 ± 0.028 | 302.8 ± 6.0 | Yes | |
| PM J11302+0735 | b |
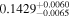
|
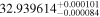
|
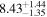
|
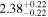
|
Clo17, Sar18 | 1.293 ± 0.021 | 296.8 ± 4.8 | Yes |
| c |
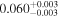
|
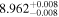
|
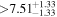
|
(>2.66) | Clo17 | 7.33 ± 0.12 | 458.0 ± 7.3 | ⋯ | |
| CD-31 9113 | b |
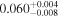
|
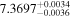
|

|
(>2.19) | Tuo14 | 9.43 ± 0.65 | 487.7 ± 33.4 | ⋯ |
| c | 3.6 |
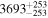
|
44.6 | ( 7.73) 7.73) |
Del13 | 0.0026 | 63 | ⋯ | |
| Ross 1003 | b |
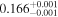
|
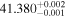
|
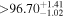
|
(>11.9) | Tri18 | 0.5440 ± 0.0061 | 239.0 ± 2.7 | Yes |
| c |
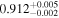
|
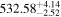
|
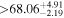
|
(>9.40) | Tri18 | 0.01802 ± 0.00021 | 102.0 ± 1.2 | ⋯ | |
| Ross 905 | b |
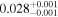
|
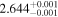
|
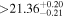
|
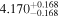
|
Mac14, Tri18 | 30.48 ± 0.45 | 653.9 ± 9.7 | ⋯ |
| LP 613-39 | b |
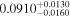
|
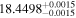
|
(5.83) |
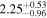
|
Sch16 | 1.470 ± 0.054 | 306.4 ± 11.3 | Yes |
| FI Vir | b |
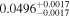
|
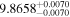
|
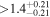
|
(>1.11) | Bon18b | 1.556 ± 0.023 | 310.8 ± 4.5 | ⋯ |
| K2-152 | b |
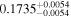
|
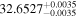
|
(8.30) |
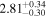
|
Hir18 | 2.944 ± 0.054 | 364.6 ± 6.6 | ⋯ |
| K2-153 | b |
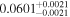
|
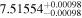
|
(4.89) |
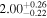
|
Hir18 | 14.82 ± 0.33 | 546 ± 12 | ⋯ |
| K2-137 | b |

|
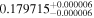
|
(0.65) |
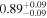
|
Smi18 | 841 ± 18 | 1499 ± 33 | ⋯ |
| K2-154 | b |
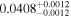
|
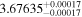
|
(6.08) |
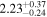
|
Hir18 | 59.04 ± 0.96 | 772 ± 13 | ⋯ |
| c |
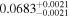
|
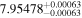
|
(5.48) |
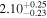
|
Hir18 | 21.07 ± 0.34 | 596.3 ± 9.7 | ⋯ | |
| Ross 1020 | b |

|
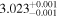
|
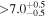
|
(>2.54) | Luq18 | 12.16 ± 0.16 | 519.7 ± 6.6 | ⋯ |
| HD 122303 | b |
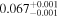
|
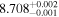
|
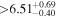
|
(>2.42) | Tri18 | 9.66 ± 0.16 | 490.6 ± 8.2 | ⋯ |
| Proxima Cen | b |
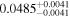
|
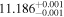
|

|
(>1.07) | Ang16 | 0.653 ± 0.017 | 250.2 ± 6.4 | Yes |
| K2-240 | b |
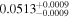
|
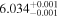
|

|
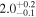
|
Die18 | 23.88 ± 0.58 | 615 ± 15 | ⋯ |
| c |
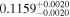
|
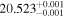
|
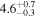
|
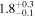
|
Die18 | 4.68 ± 0.11 | 409 ± 10 | ⋯ | |
| HO Lib | b |
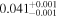
|
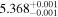
|

|
(>4.03) | Tri18 | 7.14 ± 0.10 | 455.0 ± 6.4 | ⋯ |
| c |
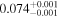
|
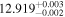
|
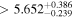
|
(>2.20) | Tri18 | 2.192 ± 0.031 | 338.6 ± 4.7 | ⋯ | |
| d |
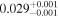
|
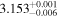
|
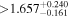
|
(>1.18) | Tri18 | 14.27 ± 0.20 | 541.0 ± 7.6 | ⋯ | |
| K2-286 | b |
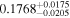
|
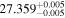
|
(5.26) |
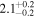
|
Die19 | 2.891 ± 0.063 | 362.9 ± 7.9 | ⋯ |
| MCC 759 | b |

|
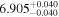
|
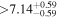
|
(>2.67) | Per17 | 17.5 ± 0.2 | 569.1 ± 6.4 | ⋯ |
| USco J161014.7-191909 | b |
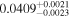
|

|
<11.76 |
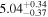
|
Dav16, Man16b | 60.9 ± 1.9 | 778 ± 25 | ⋯ |
| LP 804-27 | b | 0.36 |
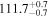
|

|
(>13.2) | App10 | 0.23 | 193 | ⋯ |
| HD 147379 | b |
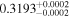
|
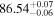
|
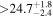
|
(>5.28) | Rei18 | 0.959 ± 0.023 | 275.4 ± 6.5 | Yes |
| MCC 767 | b |
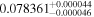
|
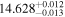
|
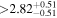
|
(>1.45) | Sua17 | 2.412 ± 0.033 | 346.8 ± 4.8 | ⋯ |
| V2306 Oph | b |
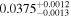
|
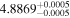
|
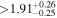
|
(>1.23) | Ast17b | 7.70 ± 0.12 | 463.6 ± 7.1 | ⋯ |
| c |
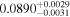
|
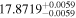
|
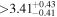
|
(>1.66) | Ast17b | 1.366 ± 0.021 | 300.9 ± 4.6 | Yes | |
| d |
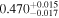
|
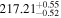
|
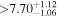
|
(>2.66) | Ast17b | 0.04899 ± 0.00077 | 130.9 ± 2.1 | ⋯ | |
| BD+25 3173 | b |

|
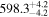
|
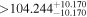
|
(>12.5) | Jon10 | 0.03372 ± 0.00036 | 119.3 ± 1.3 | ⋯ |
| LHS 3275 | b |

|
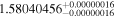
|
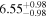
|

|
Cha09, Har13 | 19.51 ± 0.25 | 584.9 ± 7.6 | ⋯ |
| BD+11 3149 | b |
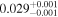
|
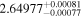
|
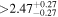
|
(>1.36) | Aff16 | 55.6 ± 1.5 | 760 ± 20 | ⋯ |
| c |
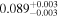
|
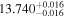
|
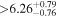
|
(>2.36) | Aff16 | 5.90 ± 0.16 | 434 ± 11 | ⋯ | |
| HD 156384C | b |
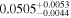
|
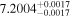
|
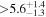
|
(>2.23) | Ang13 | 5.86 ± 0.14 | 433 ± 10 | ⋯ |
| c |
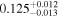
|
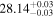
|
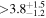
|
(>1.78) | Ang13 | 0.956 ± 0.016 | 275.2 ± 4.7 | Yes | |
| d |
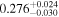
|
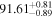
|

|
(>2.08) | Ang13 | 0.1962 ± 0.0052 | 185.2 ± 4.9 | ⋯ | |
| e |
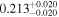
|
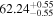
|

|
(>1.47) | Ang13 | 0.3294 ± 0.0050 | 210.9 ± 3.2 | Yes | |
| f |
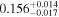
|
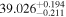
|
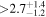
|
(>1.42) | Ang13 | 0.614 ± 0.015 | 246.4 ± 6.0 | Yes | |
| g |
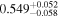
|
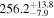
|
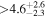
|
(>1.98) | Ang13 | 0.04958 ± 0.00092 | 131.3 ± 2.4 | ⋯ | |
| CD-46 11540 | b | 0.039 |
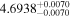
|
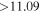
|
(>3.32) | Bon07 | 11 | 507 | ⋯ |
| CD-51 10924 | b |
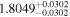
|
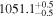
|
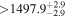
|
(>12.8) | Sah16 | 0.02763 ± 0.00050 | 113.5 ± 2.0 | ⋯ |
| c |
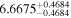
|
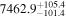
|
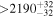
|
(>12.6) | Sah16 | 0.002024 ± 0.000037 | 59.0 ± 1.1 | ⋯ | |
| d |
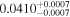
|
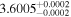
|
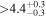
|
(>1.94) | Sah16 | 53.50 ± 0.96 | 753 ± 14 | ⋯ | |
| e |
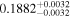
|
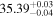
|

|
(>2.71) | Sah16 | 2.541 ± 0.046 | 351.4 ± 6.3 | ⋯ | |
| BD+68 946 | b |
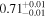
|
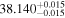
|
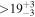
|
(>4.57) | Sta17 | 0.0439 ± 0.0010 | 127.4 ± 2.8 | ⋯ |
| CD-44 11909 | b |
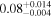
|
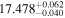
|
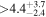
|
(>1.92) | Tuo14 | 1.268 ± 0.159 | 295 ± 37 | Yes |
| c |
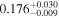
|
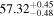
|
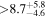
|
(>2.81) | Tuo14 | 0.262 ± 0.031 | 199 ± 24 | Yes | |
| BD+18 3421 | b |
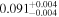
|

|
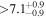
|
(>2.58) | Aff19 | 3.34 ± 0.22 | 376 ± 25 | ⋯ |
| Barnard's star | b |
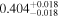
|
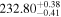
|
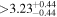
|
(>1.58) | Rib18 | 0.02180 ± 0.00044 | 106.9 ± 2.2 | ⋯ |
| Kepler-83 | b | 0.0785 |
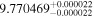
|
(7.03) |
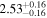
|
Row14 | 15 | 547 | ⋯ |
| c | 0.0514 |
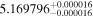
|
(4.74) |
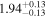
|
Row14 | 35 | 676 | ⋯ | |
| d | 0.1270 |
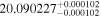
|
(6.08) |
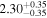
|
Row14 | 5.7 | 430 | ⋯ | |
| Kepler-446 | b |
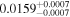
|

|
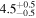
|
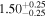
|
Mui15 | 19.61 ± 0.39 | 586 ± 12 | ⋯ |
| c |

|
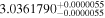
|
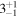
|
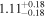
|
Mui15 | 8.11 ± 0.16 | 469.6 ± 9.3 | ⋯ | |
| d |
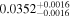
|
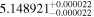
|
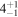
|
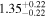
|
Mui15 | 4.008 ± 0.079 | 393.8 ± 7.8 | ⋯ | |
| Kepler-303 | b | 0.0265 |

|
(0.66) |
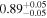
|
Row14 | 125 | 930 | ⋯ |
| c | 0.0628 |
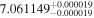
|
(1.55) |
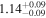
|
Row14 | 22 | 604 | ⋯ | |
| Kepler-617 | b | 0.0233 |
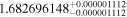
|
(2.32) |
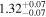
|
Mor16 | 94 | 867 | ⋯ |
| Kepler-236 | b | 0.0698 |
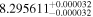
|
(3.40) |
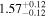
|
Row14 | 15 | 552 | ⋯ |
| c | 0.1416 |
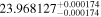
|
(4.94) |
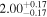
|
Row14 | 3.8 | 388 | ⋯ | |
| Kepler-235 | b | 0.035 |
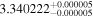
|
(5.83) |
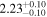
|
Row14 | 71 | 810 | ⋯ |
| c | 0.037 |
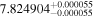
|
(2.02) |
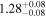
|
Row14 | 64 | 788 | ⋯ | |
| d | 0.122 |

|
(5.26) |
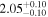
|
Row14 | 5.9 | 434 | ⋯ | |
| e | 0.213 |
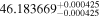
|
(5.95) |
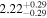
|
Row14 | 1.9 | 328 | ⋯ | |
| Kepler-52 | b | ... |
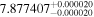
|
(6.08) |
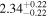
|
Row14 | 22 | 604 | ⋯ |
| c | ... |

|
(4.01) |
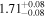
|
Row14 | 8.4 | 474 | ⋯ | |
| d | ... |
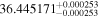
|
(4.74) |
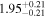
|
Row14 | 2.9 | 363 | ⋯ | |
| Kepler-155 | b | 0.056 |
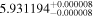
|
(5.26) |
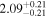
|
Row14 | 55 | 758 | ⋯ |
| c | 0.242 |
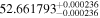
|
(5.83) |
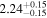
|
Row14 | 2.9 | 365 | ⋯ | |
| V1428 Aql | b |
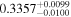
|

|
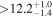
|
(>3.40) | Kam18 | 0.2891 ± 0.0035 | 204.1 ± 2.5 | Yes |
| Kepler-138 | b |

|
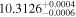
|

|
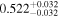
|
Jhu15 | 10.34 ± 0.14 | 499.1 ± 6.5 | ⋯ |
| c |
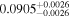
|
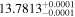
|
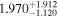
|
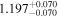
|
Jhu15 | 7.026 ± 0.092 | 453.1 ± 5.9 | ⋯ | |
| d |
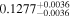
|
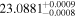
|
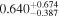
|
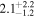
|
Jhu15 | 3.531 ± 0.046 | 381.5 ± 5.0 | ⋯ | |
| LSPM J1928+4437 | b | 0.0116 |
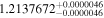
|
(0.39) |

|
Mui12b | 22 | 600 | ⋯ |
| c | 0.006 |

|
(0.33) |
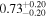
|
Mui12b | 81 | 834 | ⋯ | |
| d | 0.0154 |
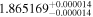
|
(0.13) |
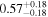
|
Mui12b | 12 | 521 | ⋯ | |
| Kepler-49 | b | 0.0642 |
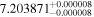
|
(6.21) |
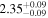
|
Row14 | 23 | 609 | ⋯ |
| c | 0.0847 |
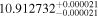
|
(5.10) |
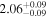
|
Row14 | 13 | 530 | ⋯ | |
| d | 0.0323 |
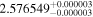
|
(3.55) |

|
Row14 | 90 | 858 | ⋯ | |
| e | 0.1208 |
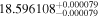
|
(3.33) |
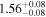
|
Row14 | 6.5 | 444 | ⋯ | |
| LSPM J1930+4149 | b |
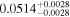
|
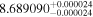
|
(1.28) |
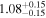
|
Age17 | 1.982 ± 0.039 | 330.2 ± 6.6 | ⋯ |
| Kepler-45 | b | 0.03 |
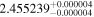
|
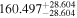
|

|
Jon12 | 90 | 856 | ⋯ |
| Kepler-231 | b | 0.0788 |
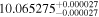
|
(4.10) |

|
Row14 | 13 | 530 | ⋯ |
| c | 0.1215 |
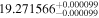
|
(4.74) |
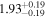
|
Row14 | 5.5 | 427 | ⋯ | |
| Kepler-54 | b | 0.0655 |
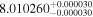
|
(5.15) |

|
Row14 | 11 | 509 | ⋯ |
| c | 0.0862 |

|
(4.23) |
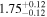
|
Row14 | 6.5 | 444 | ⋯ | |
| d | 0.1246 |
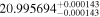
|
(3.26) |
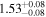
|
Row14 | 3.1 | 369 | ⋯ | |
| Kepler-252 | b | 0.0631 |
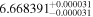
|
(1.90) |
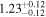
|
Row14 | 36 | 680 | ⋯ |
| c | 0.0873 |
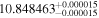
|
(5.37) |
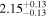
|
Row14 | 19 | 578 | ⋯ | |
| Kepler-32 | b | 0.05 |
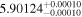
|
(5.89) |
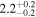
|
Fab12 | 26 | 629 | ⋯ |
| c | 0.09 |
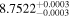
|
(4.94) |
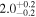
|
Fab12 | 8.0 | 469 | ⋯ | |
| d | 0.13 |
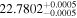
|
(7.96) |
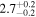
|
Fab12 | 3.9 | 390 | ⋯ | |
| e | 0.033 |
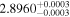
|
(4.36) |
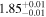
|
Fab12 | 60 | 7734 | ⋯ | |
| f | 0.013 |
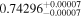
|
(0.47) |
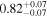
|
Fab12 | 385 | 1233 | ⋯ | |
| Kepler-125 | b | 0.0427 |
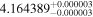
|
(6.34) |

|
Row14 | 31 | 655 | ⋯ |
| c | 0.0531 |
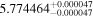
|
(0.32) |
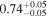
|
Row14 | 20 | 587 | ⋯ | |
| Kepler-186 | b |
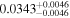
|
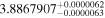
|
(1.21) |

|
Qui14 | 48.6 ± 1.2 | 735 ± 19 | ⋯ |
| c |
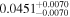
|
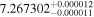
|
(2.02) |
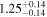
|
Qui14 | 28.09 ± 0.71 | 641 ± 16 | ⋯ | |
| d |
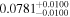
|
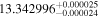
|
(2.65) |

|
Qui14 | 9.37 ± 0.24 | 487 ± 12 | ⋯ | |
| e |
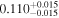
|
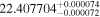
|
(2.05) |
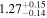
|
Qui14 | 4.72 ± 0.12 | 410 ± 10 | ⋯ | |
| f |
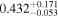
|
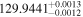
|
(1.65) |
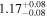
|
Tor15 | 0.306 ± 0.084 | 207 ± 57 | Yes | |
| Kepler-445 | b |

|
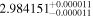
|
(3.55) |
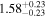
|
Mui15 | 14.79 ± 0.40 | 546 ± 15 | ⋯ |
| c |
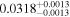
|
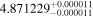
|
(6.74) |
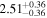
|
Mui15 | 7.70 ± 0.21 | 464 ± 13 | ⋯ | |
| d |
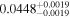
|
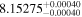
|
(1.86) |
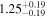
|
Mui15 | 3.87 ± 0.11 | 390 ± 11 | ⋯ | |
| Kepler-267 | b | 0.0370 |
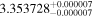
|
(5.04) |
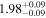
|
Row14 | 43 | 712 | ⋯ |
| c | 0.0597 |
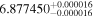
|
(5.59) |
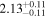
|
Row14 | 16 | 560 | ⋯ | |
| d | 0.1539 |
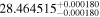
|
(5.71) |
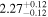
|
Row14 | 2.5 | 349 | ⋯ | |
| HD 204961 | b |
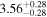
|

|
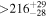
|
(>13.8) | Wit14 | 0.002304 ± 0.000088 | 61.0 ± 2.3 | ⋯ |
| c |
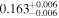
|
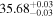
|
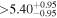
|
(>2.16) | Wit14 | 1.099 ± 0.042 | 285 ± 11 | Yes | |
| BD-05 5715 | b |
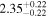
|
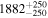
|
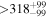
|
(>13.5) | Sta17 | 0.005115 ± 0.000077 | 74.4 ± 1.1 | ⋯ |
| c | 6.5640 | 8775 |
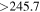
|
(>13.9) | Mon14 | 0.00066 | 45 | ⋯ | |
| LP 819-052 | b |
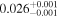
|
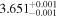
|
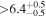
|
(>2.36) | Luq18 | 5.378 ± 0.068 | 423.8 ± 5.4 | ⋯ |
| LP 700-6 | b |
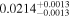
|
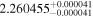
|
(6.08) |
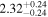
|
Hir16 | 25.50 ± 0.50 | 625 ± 12 | ⋯ |
| K2-21 | b |
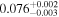
|
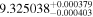
|
(4.45) |
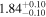
|
Dre17 | 16.93 ± 0.32 | 565 ± 11 | ⋯ |
| c |
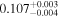
|
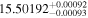
|
(7.18) |
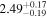
|
Dre17 | 8.54 ± 0.14 | 475.8 ± 8.0 | ⋯ | |
| LHS 3844 | b |
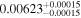
|
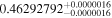
|
(2.25) |
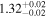
|
Van18 | 69.82 ± 0.74 | 804.5 ± 8.6 | ⋯ |
| IL Aqr | b |

|
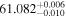
|
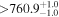
|
(>13.1) | Tri18 | 0.2823 ± 0.0066 | 202.9 ± 4.8 | Yes |
| c |
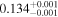
|

|
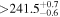
|
(>13.7) | Tri18 | 0.720 ± 0.017 | 256.4 ± 6.0 | Yes | |
| d |
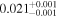
|
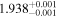
|
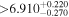
|
(>2.54) | Tri18 | 29.31 ± 0.68 | 648 ± 15 | ⋯ | |
| e |
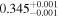
|
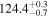
|
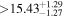
|
(>3.92) | Tri18 | 0.1086 ± 0.0025 | 159.8 ± 3.7 | ⋯ | |
| 2MUCD 12171 | b |
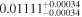
|
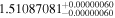
|
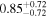
|
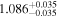
|
Gil17 | 4.357 ± 0.046 | 402.1 ± 4.3 | ⋯ |
| c |
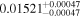
|
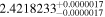
|
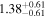
|
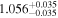
|
Gil17 | 2.325 ± 0.025 | 343.7 ± 3.7 | ⋯ | |
| d |
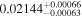
|

|
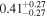
|
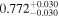
|
Gil17 | 1.170 ± 0.013 | 289.5 ± 3.1 | Yes | |
| e |
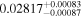
|
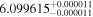
|
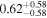
|

|
Gil17 | 0.6777 ± 0.0073 | 252.5 ± 2.7 | Yes | |
| f |
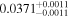
|
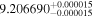
|
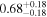
|
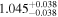
|
Gil17 | 0.3907 ± 0.0042 | 220.0 ± 2.3 | Yes | |
| g |
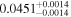
|

|
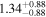
|

|
Gil17 | 0.2644 ± 0.0028 | 199.6 ± 2.1 | Yes | |
| hr |
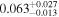
|
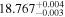
|
(0.39) |
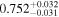
|
Gil17, Lug17 | 0.136 ± 0.030 | 169 ± 38 |
Notes.
aThe planetary masses and radii shown in parentheses correspond to our adopted mass–radius relation. bAff16: Affer et al. (2016); Aff19: Affer et al. (2019); Age17: Angelo et al. (2017); Alm15: Almenara et al. (2015); Ang12: Anglada-Escudé et al. (2012); Ang13: Anglada-Escudé et al. (2013); Ang14: Anglada-Escudé et al. (2014); Ang16: Anglada-Escudé et al. (2016); App10: Apps et al. (2010); Ast15: Astudillo-Defru et al. (2015); Ast17a: Astudillo-Defru et al. (2017a); Ast17b: Astudillo-Defru et al. (2017b); Bak18: Bakos et al. (2018); Bay18: Bayliss et al. (2018); Bid14: Biddle et al. (2014); Bon07: Bonfils et al. (2007); Bon11: Bonfils et al. (2011); Bon13b: Bonfils et al. (2013b); Bon17: Bonfils et al. (2018b); Bon18a: Bonfils et al. (2018b); Bon18b: Bonfils et al. (2018a); But17: Butler et al. (2017); Cha09: Charbonneau et al. (2009); Clo17: Cloutier et al. (2017); Dav16: David et al. (2016); Del13: Delfosse et al. (2013); Die18a: (Díez Alonso et al. 2018b); Die18b: (Díez Alonso et al. 2018a); Die19: (Díez Alonso et al. 2019); Dit17: Dittmann et al. (2017); Dre17: Dressing et al. (2017);Fab12: Fabrycky et al. (2012); Fei19: Feinstein et al. (2019); Gil17: Gillon et al. (2017); Gil17: Gillon et al. (2017); Gun19: Günther et al. (2019); Har13: Harpsœet al. (2013); Har15: Hartman et al. (2015); Hir16: Hirano et al. (2016); Hir18: Hirano et al. (2018); Hob18: Hobson et al. (2018); Hob19: Hobson et al. (2019); How10: Howard et al. (2010); Jhu15: Jontof-Hutter et al. (2015); Jon10: Johnson et al. (2010); Jon12: Johnson et al. (2012); Kam18: Kaminski et al. (2018); Liv19: Livingston et al. (2019); LoC13: Lo Curto et al. (2013); Lug17: Luger et al. (2017); Luq18: Luque et al. (2018); Mac14: Maciejewski et al. (2014); Man16a: Mann et al. (2016a); Man16b: Mann et al. (2016b); Men19: Ment et al. (2019); Mon14: Montet et al. (2014); Mor16: Morton et al. (2016); Mui12: Muirhead et al. (2012b); Mui15: Muirhead et al. (2015); Obe16: Obermeier et al. (2016); Per17: Perger et al. (2017); Per19: Perger et al. (2019); Pin18: Pinamonti et al. (2018); Qui14: Quintana et al. (2014); Rei18: Reiners et al. (2018); Rob13: Robertson et al. (2013); Row14: Rowe et al. (2014);Sah16: Sahlmann et al. (2016); San15: Sanchís-Ojeda et al. (2015); Sar18: Sarkis et al. (2018); Sch16: Schlieder et al. (2016); Sin16: Sinukoff et al. (2016); Sou17: Southworth et al. (2017); Smi18: Smith et al. (2018); Sta17: Stassun et al. (2017); Sua17: Suárez Mascareño et al. (2017); Tor15: Torres et al. (2015); Tri18: Trifonov et al. (2018); Tuo14: Tuomi et al. (2014); Van18: Vanderspek et al. (2019); Wel17: Wells et al. (2018); Wit14: Wittenmyer et al. (2014). cBonfils et al. (2011) gave true mass for LP 905-36 calculated with a Markov chain analysis,
 , but we adopt the minimum mass,
, but we adopt the minimum mass,  , for consistency.
, for consistency.
A machine-readable version of the table is available.
Footnotes
- 6
- 7
- 8
We follow this naming priority order: common (e.g., Proxima, Luyten's star), Bayer (e.g., α Cen C), Flamsteed/variable (e.g., 3 Lyr, IL Aqr, V1428 Aql), Lalande, Henry Draper, Bonner/Córdoba Durchmusterung, Wolf, Ross, Gliese-Jahreiss (but GJ number is always given), Luyten Palomar or equivalent, and discovery names (e.g., MCC, PM, 2MUCD, Kepler, K2, KOI, EPIC).
- 9
- 10
Leggett et al. (2001) tabulated L = (27 ± 66)10−4 L⊙ for LP 656–38.
- 11
aMoon = 3.84399 × 108 m, MMoon = 7.346 × 1022 kg, and R⊕ = 6.3781366 × 106 m.
- 12
- 13
In the last stages of revision of this paper, we became aware of an independent study of the exomoon hypothesis around Ross 1003, by T. Trifonov et al. (2019, in preparation).
- 14
- 15
MGan = 1.48 × 1023 kg; RGan = 2.6341 × 106 m.
- 16