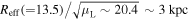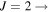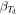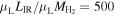Abstract
Dusty star-forming galaxies at high redshift (1 < z < 3) represent the most intense star-forming regions in the universe. Key aspects to these processes are the gas heating and cooling mechanisms, and although it is well known that these galaxies are gas-rich, little is known about the gas excitation conditions. Only a few detailed radiative transfer studies have been carried out owing to a lack of multiple line detections per galaxy. Here we examine these processes in a sample of 24 strongly lensed star-forming galaxies identified by the Planck satellite (LPs) at z ∼ 1.1–3.5. We analyze 162 CO rotational transitions (ranging from Jup = 1 to 12) and 37 atomic carbon fine-structure lines ([C i]) in order to characterize the physical conditions of the gas in the sample of LPs. We simultaneously fit the CO and [C i] lines and the dust continuum emission, using two different non-LTE, radiative transfer models. The first model represents a two-component gas density, while the second assumes a turbulence-driven lognormal gas density distribution. These LPs are among the most gas-rich, IR-luminous galaxies ever observed (μL L⊙;
L⊙;  μLMISM
μLMISM = (2.7 ± 1.2) × 1012 M⊙, with μL ∼ 10–30 the average lens magnification factor). Our results suggest that the turbulent interstellar medium present in the LPs can be well characterized by a high turbulent velocity dispersion (
= (2.7 ± 1.2) × 1012 M⊙, with μL ∼ 10–30 the average lens magnification factor). Our results suggest that the turbulent interstellar medium present in the LPs can be well characterized by a high turbulent velocity dispersion ( ΔVturb
ΔVturb ∼ 100 km s−1) and ratios of gas kinetic temperature to dust temperature
∼ 100 km s−1) and ratios of gas kinetic temperature to dust temperature  Tkin/Td
Tkin/Td ∼ 2.5, sustained on scales larger than a few kiloparsecs. We speculate that the average surface density of the molecular gas mass and IR luminosity,
∼ 2.5, sustained on scales larger than a few kiloparsecs. We speculate that the average surface density of the molecular gas mass and IR luminosity,  ∼ 103–4 M⊙ pc−2 and
∼ 103–4 M⊙ pc−2 and  ∼ 1011–12 L⊙ kpc−2, arise from both stellar mechanical feedback and a steady momentum injection from the accretion of intergalactic gas.
∼ 1011–12 L⊙ kpc−2, arise from both stellar mechanical feedback and a steady momentum injection from the accretion of intergalactic gas.
Export citation and abstract BibTeX RIS
1. Introduction
Star-forming galaxies at redshifts z ∼ 1–3 probe the cosmic epoch when most of the stellar mass assembly in the universe took place (Madau & Dickinson 2014, and references therein). A better understanding of star formation (SF) during this epoch is therefore imperative to understand SF across cosmic time. Locally, less than 5% of the galaxy population has a star formation rate (SFR) that is significantly higher than the empirical main sequence for star-forming galaxies, i.e., the tight correlation (∼0.3 dex) between the SFR and stellar mass, M⋆ (Brinchmann et al. 2004; Elbaz et al. 2007, 2011; Noeske et al. 2007; Goto et al. 2011; Rodighiero et al. 2011; Sargent et al. 2012; Whitaker et al. 2012, 2014; Salmon et al. 2015). These often-called starburst galaxies, with an IR luminosity LIR ∼ (0.1–5) × 1012 L⊙ (e.g., Sanders & Mirabel 1996; Downes & Solomon 1998), become increasingly more common at high z. In fact, (sub)millimeter number counts reveal that galaxies with LIR > 1012–13 L⊙, at z > 0.5, are many hundreds of times more likely to exist than in the local universe (Blain et al. 2002; Chapman et al. 2005; Berta et al. 2011; Magnelli et al. 2011; Béthermin et al. 2012; Magnelli et al. 2013; Casey et al. 2013, 2014; Geach et al. 2013; Simpson et al. 2014; Strandet et al. 2016; Brisbin et al. 2017). Meanwhile, the cosmic molecular gas density also peaks at z ∼ 1–3 (Decarli et al. 2014, 2016a, 2016b, 2019; Walter et al. 2014; Lentati et al. 2015; Pavesi et al. 2018; Liu et al. 2019; Riechers et al. 2019). This suggests a strong link between molecular gas and SF. Rest-frame far-IR (FIR) measurements of spectral lines and thermal dust continuum emission have been used to investigate the cooling and heating processes of the interstellar medium (ISM) in star-forming galaxies; however, the physical conditions at high z are still, in general, poorly investigated (Popesso et al. 2012; Bothwell et al. 2013; Carilli & Walter 2013; Genzel et al. 2013; Yang et al. 2017; Tacconi et al. 2018, 2020; Aravena et al. 2020; Birkin et al. 2020; Boogaard et al. 2020; Lenkić et al. 2020).
Turbulence regulates SF within cold and dense molecular clouds in most star-forming regions, and turbulence-regulated feedback seems to properly describe the main characteristics of the star-forming ISM (Shu et al. 1987; Elmegreen & Scalo 2004; Krumholz & McKee 2005; McKee & Ostriker 2007; Krumholz 2014). A lognormal probability distribution function (pdf) is often used to describe both the molecular gas velocity dispersion and volume density (Vazquez-Semadeni 1994; Padoan et al. 1997; Ostriker 1998; Klessen 2000; Wada & Norman 2001; Kowal et al. 2007; Narayanan et al. 2008a, 2008b; Krumholz et al. 2009b; Hopkins et al. 2012a, 2012b, 2013; Molina et al. 2012). This is because the turbulent activity sets the local gas density as a consequence of randomly distributed shocks that compress the gas. These processes eventually converge toward a lognormal distribution of density due to the central limit theorem (Vazquez-Semadeni 1994; Kevlahan & Pudritz 2009; Krumholz 2014). Such turbulent models are supported by observational evidence using optically thin, diffuse, and dense molecular gas tracers of clouds within the Milky Way (e.g., Ginsburg et al. 2013). A commonly used simplification to deal with these complex models is to adopt the large velocity gradient (LVG) approximation (Goldreich & Kwan 1974; Scoville & Solomon 1974) to model the photon escape probabilities within large-scale velocity flows. This assumption is applicable for clouds in the Milky Way, where the local thermal motions are much smaller than flow velocities, although non-local thermodynamic equilibrium (non-LTE) gas conditions may be present. The radial motion assumed in early applications of non-LTE LVG models would lead to higher SF efficiencies than observed, leading to the conclusion that a form of turbulent feedback must be present in the ISM to regulate SF (Zuckerman & Evans 1974; Zuckerman & Palmer 1975). In addition, turbulent motion is set at the "driving scale" (e.g., Elmegreen & Scalo 2004; Scalo & Elmegreen 2004), determined by the largest physical size of the system. Diverse studies have found that gas turbulence increases as a function of z, suggesting that such SF processes cannot be maintained for long periods of time (several orbital times)—particularly in the most extreme star-forming galaxies (Kassin et al. 2012; Wisnioski et al. 2015; Johnson et al. 2018; Übler et al. 2019). How the turbulent ISM behaves at high z, given the strong cosmic evolution of star-forming gas, is still an open question.
Star-forming galaxies at high z may have turbulent SF extending many kiloparsecs beyond their center, with total molecular gas masses up to an order of magnitude larger than local starbursts (Tacconi et al. 2006; Hodge 2010; Ivison et al. 2010; Hodge et al. 2016; Kirkpatrick et al. 2017). Therefore, it is crucial to derive the bulk molecular gas mass content in these host galaxies in order to properly quantify the SF activity as a function of the molecular gas properties. The main challenge in studying the star-forming gas is that cloud collapse requires cold environments, with T ≤ 100 K, yet the lowest-energy transitions of H2 are much higher than these temperatures. Therefore, H2 is unable23 to trace the total column density (i.e., total mass) of gas (e.g., 1%–30% of the gas column density; Roussel et al. 2007). Carbon monoxide (CO), the second most abundant molecule in the ISM, is almost exclusively excited by collisions with H2 at a wide range of gas densities. The properties of CO-emitting gas are useful to provide insight into the global molecular gas properties, and CO has therefore been used to estimate H2 gas column densities, and further, the bulk molecular gas mass content of star-forming galaxies at high z.
The CO line luminosity to molecular gas mass conversion factor, αCO, has been reviewed by several detailed studies (Magdis et al. 2011; Genzel et al. 2012; Narayanan et al. 2012, 2015; Schruba et al. 2012; Bolatto et al. 2013; Hunt et al. 2015; Amorín et al. 2016; Accurso et al. 2017). The CO (1−0) and CO (2−1) rotational transitions, as well as their less optically thick isotopologues (13CO, C18O), have been vital in determining the  -to-
-to- conversion factor, αCO. The Galactic value is αCO ∼ 4 M⊙ (K km s−1 pc2)−1, whereas the canonical value for local starburst galaxies is αCO ∼ 0.8 M⊙ (K km s−1 pc2)−1 (Downes & Solomon 1998). CO traces diffuse and dense gas; however, the atomic carbon, fine-structure line transitions ([C i] lines) are able to trace mostly diffuse gas (Glover & Clark 2012; Israel et al. 2015). [C i] is an additional tracer capable of determining the molecular H2 gas mass (Weiß et al. 2003, 2005a). Efforts to calibrate the [C i] transitions as a tracer of the molecular gas mass and attempts to constrain the gas-phase carbon abundance have grown significantly, including high-z massive star-forming galaxies on the main sequence and bright quasars (Walter et al. 2011; Alaghband-Zadeh et al. 2013; Bothwell et al. 2017; Valentino et al. 2018, 2020b; Dannerbauer et al. 2019). This is mostly based on the relative increase in detection efficiency of the [C i] ground transition as it gets redshifted at z > 1 into millimeter wavelengths, due to the higher photon energy in the [C i] lines. This makes it easier to detect than the faint ground-state CO (1−0) line. For the cold (T ∼ 20 K) and low-density (log(
conversion factor, αCO. The Galactic value is αCO ∼ 4 M⊙ (K km s−1 pc2)−1, whereas the canonical value for local starburst galaxies is αCO ∼ 0.8 M⊙ (K km s−1 pc2)−1 (Downes & Solomon 1998). CO traces diffuse and dense gas; however, the atomic carbon, fine-structure line transitions ([C i] lines) are able to trace mostly diffuse gas (Glover & Clark 2012; Israel et al. 2015). [C i] is an additional tracer capable of determining the molecular H2 gas mass (Weiß et al. 2003, 2005a). Efforts to calibrate the [C i] transitions as a tracer of the molecular gas mass and attempts to constrain the gas-phase carbon abundance have grown significantly, including high-z massive star-forming galaxies on the main sequence and bright quasars (Walter et al. 2011; Alaghband-Zadeh et al. 2013; Bothwell et al. 2017; Valentino et al. 2018, 2020b; Dannerbauer et al. 2019). This is mostly based on the relative increase in detection efficiency of the [C i] ground transition as it gets redshifted at z > 1 into millimeter wavelengths, due to the higher photon energy in the [C i] lines. This makes it easier to detect than the faint ground-state CO (1−0) line. For the cold (T ∼ 20 K) and low-density (log( ) ∼ 2 cm−3) ISM, dominating the emission in the Milky Way (Dame et al. 1986; Bronfman et al. 1988; Fixsen et al. 1999; García et al. 2014), the CO (1−0) line luminosity has traditionally been used as a tracer of the total molecular gas content (Bolatto et al. 2013), as higher molecular rotational levels are poorly populated under these conditions. Following early studies in the Milky Way, this approach has been widely applied to determine the molecular gas content in nearby star-forming galaxies. The general scenario may differ for higher-excitation gas (or increased SF activity), as the higher-J populations can contribute a more significant fractional contribution to the CO partition function. For intense star-forming environments, where the mean gas density is larger than 103–4 cm−3 and/or the gas kinetic temperature is higher than 20 K, the CO (2−1) and CO (3−2) and even higher rotational transitions begin to contribute a higher fraction to the partition function, as less molecules sit at the Jup = 1 state. Thus, these low-J lines can trace comparable, if not larger, fractions of the total CO column densities (and thus more molecular gas) in relation to the CO (1−0) line. This highlights the need to measure multiple CO transitions and conduct a proper modeling of the line intensities to obtain meaningful conversion factors for star-forming galaxies at z > 1.
) ∼ 2 cm−3) ISM, dominating the emission in the Milky Way (Dame et al. 1986; Bronfman et al. 1988; Fixsen et al. 1999; García et al. 2014), the CO (1−0) line luminosity has traditionally been used as a tracer of the total molecular gas content (Bolatto et al. 2013), as higher molecular rotational levels are poorly populated under these conditions. Following early studies in the Milky Way, this approach has been widely applied to determine the molecular gas content in nearby star-forming galaxies. The general scenario may differ for higher-excitation gas (or increased SF activity), as the higher-J populations can contribute a more significant fractional contribution to the CO partition function. For intense star-forming environments, where the mean gas density is larger than 103–4 cm−3 and/or the gas kinetic temperature is higher than 20 K, the CO (2−1) and CO (3−2) and even higher rotational transitions begin to contribute a higher fraction to the partition function, as less molecules sit at the Jup = 1 state. Thus, these low-J lines can trace comparable, if not larger, fractions of the total CO column densities (and thus more molecular gas) in relation to the CO (1−0) line. This highlights the need to measure multiple CO transitions and conduct a proper modeling of the line intensities to obtain meaningful conversion factors for star-forming galaxies at z > 1.
Local measurements of the CO ladder in large samples of star-forming and starburst systems have been conducted using the Herschel SPIRE (and HIFI; Rangwala et al. 2011; Liu et al. 2015; Rosenberg et al. 2015; Kamenetzky et al. 2016; Lu et al. 2017). On average, the majority of the SF in local starburst galaxies is confined to the central few hundred parsecs of the Galactic nucleus. Most extreme IR luminosities in the local universe are induced by merger-driven processes, although, in general, there is a strong presence of warm and diffuse molecular gas (see, e.g., Downes & Solomon 1998), well traced by the mid- to high-J CO lines (Rosenberg et al. 2015; Kamenetzky et al. 2016). Constraints on such galaxy-wide molecular ISM properties at z > 1 have been limited to large integration times required to sample the low-, mid-, and high-J CO lines. Less than 20 yr ago, only ∼40 galaxies at z > 1 had been detected in CO emission (Solomon & Vanden Bout 2005; Omont 2007). Carilli & Walter (2013) reviewed ∼200 galaxies, most with a single line detection (Jup = 2–5). At the time, only 11 high-z galaxies had one (or both) [C i] line detection(s) (Weiß et al. 2005a; Walter et al. 2011; Carilli & Walter 2013).
Strong gravitational lensing of high-z star-forming galaxies offers a unique way to examine highly magnified molecular gas. The method for selecting strongly lensed dusty galaxy candidates, at z > 1, is primarily based on unusually bright (sub)millimeter fluxes compared to the expected steep drop-off in (sub)millimeter number counts (e.g., Negrello et al. 2007, 2010). This method has since identified a large number across the extragalactic sky, i.e., more than 100 lensed candidates at z > 1 (Ivison et al. 2010; Vieira et al. 2010, 2013; Bussmann et al. 2013, 2015; Wardlow et al. 2013; Weiß et al 2013; Cañameras et al. 2015; Harrington et al. 2016; Strandet et al. 2016; Díaz-Sánchez et al. 2017; Negrello et al. 2017; Bakx et al. 2018). The lensed population of dusty star-forming galaxies selected by the South Pole Telescope (SPT), Herschel Space Observatory, and Planck has now been detected in more than two CO transitions (e.g., Spilker et al. 2016; Strandet et al. 2017; Yang et al. 2017; Bakx et al. 2020; this work). The Herschel-selected, strongly lensed galaxy sample (Bussmann et al. 2013) offered the first systematic approach to producing a statistically significant sample of CO/[C i] lines (Yang et al. 2017), followed by a compilation in 11 Planck- and Herschel-selected lensed galaxies (Cañameras et al. 2018b), including four galaxies with both [C i] lines detected (Nesvadba et al. 2019). The IR-to-CO luminosity relations of local starbursts and high-z star-forming galaxies explored by Greve et al. (2014) indicate that the ISM radiation field is an important component to consider when understanding CO line excitation, yet this investigation was limited to 23 unlensed and 21 lensed dusty star-forming systems—all with more than three frequency measurements of the dust continuum and usually a single CO line detection. Most previous studies used only single- and/or double-component gas-emitting regions to reproduce the observed CO emission, excluding the simultaneous modeling of the available [C i] emission, but also ignoring the role of the dust continuum emission as a heating source of the gas.
In this work, we apply state-of-the-art non-LTE models to ∼200 CO and [C i] emission lines, from single-dish line measurements, for a flux-limited sample of 24 lensed galaxies identified by the Planck satellite. This sample builds off of our pilot Planck and Herschel selection in Harrington et al. (2016), expanded since then (D. Berman et al. 2021, in preparation). We have selected 24 of these galaxies to investigate the physical gas conditions responsible for driving such bright apparent FIR luminosities ( L⊙). We have a systematic focus on detecting the rise, peak, and turnover in the CO excitation ladder in order to investigate the gas volume densities and turbulent properties, the relationship between the gas kinetic temperature and dust temperature, and the derivation of αCO. We follow a novel approach when modeling all emission lines detected based on a turbulence-driven gas density pdf. Unlike most high-z studies, we have simultaneously modeled these lines in the presence of both dust continuum radiation field and cosmic microwave background (CMB) radiation as background excitation sources. This work is organized as follows. In Section 2 we describe the sample selection and ancillary dust photometry of the 24 strongly lensed galaxies in our sample. In Section 3 we provide the details of the novel GBT, IRAM 30 m, and APEX single-dish measurements of the CO ladder, ranging from Jup = 1 to 12, and both [C i] lines. In Section 4 we provide a summary of the emission-line profiles. We summarize the model and model assumptions we applied in Section 5. In Section 6 we discuss our main results, and in Section 7 we provide an interpretation of the physical gas conditions of these extreme starburst galaxies. Our conclusions are summarized in Section 8. We adopt a fiducial ΛCDM cosmology with
L⊙). We have a systematic focus on detecting the rise, peak, and turnover in the CO excitation ladder in order to investigate the gas volume densities and turbulent properties, the relationship between the gas kinetic temperature and dust temperature, and the derivation of αCO. We follow a novel approach when modeling all emission lines detected based on a turbulence-driven gas density pdf. Unlike most high-z studies, we have simultaneously modeled these lines in the presence of both dust continuum radiation field and cosmic microwave background (CMB) radiation as background excitation sources. This work is organized as follows. In Section 2 we describe the sample selection and ancillary dust photometry of the 24 strongly lensed galaxies in our sample. In Section 3 we provide the details of the novel GBT, IRAM 30 m, and APEX single-dish measurements of the CO ladder, ranging from Jup = 1 to 12, and both [C i] lines. In Section 4 we provide a summary of the emission-line profiles. We summarize the model and model assumptions we applied in Section 5. In Section 6 we discuss our main results, and in Section 7 we provide an interpretation of the physical gas conditions of these extreme starburst galaxies. Our conclusions are summarized in Section 8. We adopt a fiducial ΛCDM cosmology with  , Ωm = 0.286, and
, Ωm = 0.286, and  throughout this paper (Bennett et al. 2014).24
throughout this paper (Bennett et al. 2014).24
2. Sample
2.1. Selection
Here we outline our sample of strongly lensed Planck-selected, dusty star-forming galaxies, hereafter "LPs" (Table 1). Our sample of 24 LPs began with a Planck and Herschel cross-match identification of eight objects (8/24) with continuum detections at 857 GHz (Harrington et al. 2016) greater than 100 mJy. The remaining 16/24 LPs were selected based on continuum detections by Planck, at 857, 545, and/or 353 GHz in the maps of all the available, clean extragalactic sky. These bright Planck point sources were then analyzed through a filtering process using a WISE color selection for the four WISE bands (3.4, 4.6, 12, 22 μm; Yun et al. 2008; D. Berman et al. 2021, in preparation). Other methods to identify strong gravitational lenses using (sub)millimeter data were independently verified by other teams using Planck and Herschel color criteria (Cañameras et al. 2015). The 24 LPs presented in these analyses include eight systems identified by Cañameras et al. (2015). The use of Planck and WISE data resulted in the discovery of the brightest known, dusty starburst galaxy at z > 1, the "Cosmic Eyebrow" (Díaz-Sánchez et al. 2017; Dannerbauer et al. 2019), which has also been independently recovered as one of the LPs presented in this survey work. Note that LPsJ1329 corresponds to the location on the sky associated with the Cosmic Eyebrow-A lens component (Dannerbauer et al. 2019). Table 1 shows the size of the lensed emission for each of the LPs, in which there are 21/24 with lens sizes ≤10''. Half of the LPs are galaxy–galaxy lenses, while the other half are a mix of cluster or group lensing. The foreground lens galaxies have a negligible contribution to the observed FIR emission of the lensed galaxy (Harrington et al. 2016). The LPs have CO-based spectroscopic redshifts ranging from zCO ∼ 1.1 to 3.6 (Harrington et al. 2016, 2018; Cañameras et al. 2018b; this work). They are comparable or brighter in CO and FIR luminosity than other strongly lensed SPT- (Weiß et al 2013; Strandet et al. 2016, 2017) or Herschel-selected; dusty star-forming galaxies (Harris et al. 2012; Bussmann et al. 2013, 2015; Yang et al. 2017). The Planck and Herschel wavelength selections preferentially target z ∼ 2–3 galaxies, versus the millimeter-selected SPT sources with a median closer to z ∼ 4, although with a wide range between z ∼ 2 and 7 (Weiß et al 2013; Spilker et al. 2016; Strandet et al. 2016; Reuter et al. 2020).
Table 1. Sample Summary
| ID | R.A. | Decl. | zfg | z | μL |
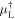
|
Lens Size | References |
|---|---|---|---|---|---|---|---|---|
| (RAh:RAm:RAs) | (DEd;DEm;DEs) | ('') | ||||||
| LPsJ0116 | 01:16:46.77 | −24:37:01.90 | 0.4 | 2.12453 | ⋯ | 23 | ∼4.5GG | 1 |
| LPsJ0209 | 02:09:41.3 | 00:15:59.00 | 0.202 | 2.55274 | 7–22 | 58 | ∼3GG | 2, 3, 4, 5, 6, 7, 8 |
| LPsJ0226 | 02:26:33.98 | 23:45:28.3 | 0.34 | 3.11896 | ⋯ | 40 | ∼3.5GG | 1, 8 |
| LPsJ0305 | 03:05:10.62 | −30:36:30.30 | 0.1-0.5 | 2.26239 | ⋯ | 18 | ∼2GG | 1 |
| LPsJ0748 | 07:48:51.72 | 59:41:53.5 | 0.402 | 2.75440 | ⋯ | 21 | ∼13GC | 1, 9, 10 |
| LPsJ0846 | 08:46:50.16 | 15:05:47.30 | 0.1 | 2.66151 | ⋯ | 27 | ∼10GC | 1 |
| LPsJ105322 | 10:53:22.60 | 60:51:47.00 | 0.837 | 3.54936 | 5–12 | 41 | ∼6GG | 1, 11, 12, 13 |
| LPsJ105353 | 10:53:53.00 | 05:56:21.00 | 1.525 | 3.00551 | 9–48 | 20 | ∼1.5GG | 2, 11, 12, 13, 14, 15, 16 |
| LPsJ112714 | 11:27:14.50 | 42:28:25.00 | 0.33-0.35 | 2.23639 | 20–35 | 25 | ∼13GC | 2, 11, 12, 13, 17 |
| LPsJ112713 | 11:27:13.44 | 46:09:24.10 | 0.415 | 1.30365 | ⋯ | 21 | ∼1.5GG | 1 |
| LPsJ1138 | 11:38:05.53 | 32:57:56.90 | 0.6 | 2.01833 | ⋯ | 10 | ∼1GG | 1 |
| LPsJ1139 | 11:39:21.74 | 20:24:50.90 | 0.57 | 2.85837 | 6–8 | 19 | ∼1GG | 1, 11, 12 |
| LPsJ1202 | 12:02:07.60 | 53:34:39.00 | 0.212 | 2.44160 | ⋯ | 25 | ∼5–10GC | 2, 11, 12, 16 |
| LPsJ1322 | 13:22:17.52 | 09:23:26.40 | ⋯ | 2.06762 | ⋯ | 20 | ∼10GC | 1 |
| LPsJ1323 | 13:23:02.90 | 55:36:01.00 | 0.47 | 2.41671 | 9–12 | 25 | ∼10GC | 2, 11, 12, 16 |
| LPsJ1326 | 13:26:30.25 | 33:44:07.40 | 0.64 | 2.95072 | 4–5 | 33 | ∼1.5GG | 1, 18, 19 |
| LPsJ1329 | 13:29:34.18 | 22:43:27.30 | 0.443 | 2.04008 | 9–13 | 31 | ∼11GC | 1, 19, 20, 21 |
| LPsJ1336 | 13:36:34.94 | 49:13:13.60 | 0.28 | 3.25477 | ⋯ | 24 | ∼1.5GG | 1 |
| LPsJ1428 | 14:28:23.90 | 35:26:20.00 | ⋯ | 1.32567 | ⋯ | 4 | ∼1GG | 2, 22, 23, 24, 25, 26 |
| LPsJ1449 | 14:49:58.59 | 22:38:36.80 | ⋯ | 2.15360 | ⋯ | 8 | ∼10GC | 1 |
| LPsJ1544 | 15:44:32.35 | 50:23:43.70 | 0.673 | 2.59884 | 10–17 | 10 | ∼7GC | 1, 11, 12, 13, 27 |
| LPsJ1607 | 16:07:22.6 | 73:47:03 | 0.65 | 1.48390 | ⋯ | 4 | ∼1GG | 2, 16 |
| LPsJ1609 | 16:09:17.80 | 60:45:20.00 | 0.45 | 3.25550 | 12–16 | 44 | ∼7GC | 2, 11, 12, 13, 16 |
| LPsJ2313 | 23:13:56.64 | 01:09:17.70 | 0.56 | 2.21661 | ⋯ | 57 | ∼3GG | 1 |
Note. Foreground lens redshifts, zfg, are reported in references. z is the average redshift of the LPs based on all CO/[C i] line detections. μL = lens magnification factor range. Measured with single-line/single-band CO/dust emission or HST near-IR imaging.  = estimated using Tully–Fisher method (see Appendix A). GG = galaxy–galaxy lens. The lens arc size corresponds to the effective Einstein radius, or the inferred circular radius. GC = galaxy–galaxy cluster (or group) lens. The lens arc size corresponds to the largest lens arclet or effective Einstein radius.
= estimated using Tully–Fisher method (see Appendix A). GG = galaxy–galaxy lens. The lens arc size corresponds to the effective Einstein radius, or the inferred circular radius. GC = galaxy–galaxy cluster (or group) lens. The lens arc size corresponds to the largest lens arclet or effective Einstein radius.
References. (1) D. Berman et al. 2021, in preparation; (2) Harrington et al. 2016; (3) Harrington et al. 2019; (4) Geach et al. 2015; (5) Su et al. 2017; (6) Geach et al. 2018; (7) Rivera et al. 2019; (8) P. Kamieneski et al. 2021, in preparation; (9) Khatri & Gaspari 2016; (10) Amodeo et al. 2018; (11) Cañameras et al. 2015; (12) Cañameras et al. 2018b; (13) Frye et al. 2019; (14) Cañameras et al. 2017b; (15) Cañameras et al. 2017a; (16) Harrington et al. 2018; (17) Cañameras et al. 2018a; (17) Bussmann et al. 2013; (18) Yang et al. 2017; (19) Díaz-Sánchez et al. 2017; (20) Dannerbauer et al. 2019; (21) Iglesias-Groth et al. 2017; (22) Borys et al. 2006; (23) Iono et al. 2009; (24) Sturm et al. 2010; (25) Stacey et al. 2010; (26) Hailey-Dunsheath et al. 2012; (27) Nesvadba et al. 2019.
A machine-readable version of the table is available.
Download table as: DataTypeset image
Our selection method only picks out submillimeter-bright point sources, and the WISE data assist us in interpreting that these systems do not have the same mid-IR characteristics as the luminous WISE-selected, dust-obscured QSOs (Tsai et al. 2015). The prevalence of a dust-obscured active galactic nucleus (AGN) within the LPs is uncertain; however, Harrington et al. (2016) and D. Berman et al. (2021, in preparation) have shown, using WISE and Herschel data (see methods in, e.g., Kirkpatrick et al. 2015), that the majority of the LPs have a substantial contribution to the total IR luminosity from SF activity instead of AGN activity (see also Cañameras et al. 2015). The dusty nature of the LPs has thus far resulted in the absence of stellar mass estimates, yet the extreme nature of their IR luminosities suggests that it would be reasonable to assume that they would lie above the main sequence for star-forming galaxies at these redshifts. We therefore consider them starburst galaxies, without alluding to an assumed SF history.
2.2. Continuum Data
The observed dust continuum and spectral energy distribution (SED) are used to constrain the excitation conditions, and a database of continuum measurements between 2 mm and 250 μm is compiled from new and archival photometry by Planck, Herschel, ALMA, LMT, JCMT, and IRAM 30 m telescopes. All of the ancillary (sub)millimeter photometric data used in this work can be accessed online (see abridged version in Table 9). We also provide the modeled continuum data from D. Berman et al. (2021, in preparation), and we refer the reader to more detailed information reported in the literature for previous (sub)millimeter observations with the SMA, NOEMA, and ALMA for a subset of the LPs (Bussmann et al. 2013; Cañameras et al. 2015; Harrington et al. 2016; Díaz-Sánchez et al. 2017; Su et al. 2017; Geach et al. 2018; Rivera et al. 2019; Dannerbauer et al. 2019). With the exception of the sources with ALMA 1 mm imaging data that fully resolve the continuum structure with better than 1'' angular resolution, all other photometry comes from low-resolution observations that do not resolve the dust emission. There are 10 LPs with ALMA 1 mm continuum measurements (D. Berman et al. 2021, in preparation). Six of these 10 also have LMT-AzTEC measurements, which agree well with the comparable ALMA detection (see Table 9). The continuum measurements at λobs = 1–2 mm come from LMT-AzTEC (1.1 mm) and/or IRAM 30 m-GISMO2 (2 mm) observations (Cañameras et al. 2015; Harrington et al. 2016; D. Berman et al. 2021, in preparation), and in some cases archival SCUBA-2 850 μm data were available (Díaz-Sánchez et al. 2017; D. Berman et al. 2021, in preparation).
The measured (sub)millimeter flux densities of tens to hundreds of mJy are so large that source confusion is not relevant. An exception is the Planck data with effective resolution of 5'. Here we adopt the photometry and uncertainty that fully incorporates the confusion noise based on the measured local foreground, leading to the conservative photometric uncertainties from point sources identified in the Planck maps. The majority of the LPs have ancillary Herschel SPIRE (250, 350, 500 μm) and/or millimeter-wavelength measurements from both wide-field maps and pointed observations, which are useful to constrain the peak wavelength and the long-wavelength tail of the thermal dust emission. Additionally, previous work by Harrington et al. (2016) has shown that a minimal fraction of the FIR emission is expected to come from the foreground lens for these systems.
3. Spectral Line Observations
The number of new line measurements we present in this work is ∼70% of the following: 20 CO (1−0), 6 CO (2−1), 24 CO (3−2), 15 CO (4−3), 16 CO (5−4), 15 CO (6−5), 18 CO (7−6), 17 CO (8−7), 16 CO (9−8), 6 CO (10−9), 8 CO (11−10), 1 CO (12−11), 19 [C i] (1−0), and 18 [C i] (2−1). For a thorough analysis, we complemented our line observations with nearly 50 line measurements previously reported in the literature (Cañameras et al. 2015; Harrington et al. 2016, 2018; Cañameras et al. 2017a, 2018b; Dannerbauer et al. 2019; Nesvadba et al. 2019; D. Berman et al. 2021, in preparation), for the LPs in our catalog. In Table 2, we summarize the astronomical facilities, receiver names, observed bandwidths, and telescope beam sizes involved in the data acquisition for this work. Table 2 also includes the beam size for the LMT and ALMA/Band 3 spectral line measurements to be presented in D. Berman et al. (2021, in preparation). Both the LMT and ALMA/Band 3 observations had targeted the same CO transition, CO (2−1) or CO (3−2), with comparable line fluxes.
Table 2. Observational Facilities
| Telescope | Receiver | Frequency Coverage | Beam Size |
|---|---|---|---|
| (GHz) | (arcsec) | ||
| GBT 100 m | Ka band | 26–40 | 19–29 |
| LMT 32 m | RSR | 75–115 | 21–31 |
| ALMA | Band 3 | 85–116 | 0.4–0.6 |
| IRAM 30 m | E150 | 125–175 | 14–20 |
| IRAM 30 m | E230 | 202–274 | 9–12 |
| IRAM 30 m | E330 | 277–350 | 7–9 |
| APEX 12 m | PI230 | 200–270 | 23–31 |
| APEX 12 m | FLASH 345/460 | 268–516 | 12–17 |
Note. The largest angular scale for the ALMA spectral line observations is 4''. See Harrington et al. (2016) and D. Berman et al. (2021, in preparation) for details about the LMT and ALMA observations.
Download table as: ASCIITypeset image
3.1. GBT, IRAM 30 m, and APEX Observations
We observed the CO (1−0) line with the Ka-band receiver on the Green Bank Telescope (GBT; Pr. ID: 17B-305; PI: K. Harrington) between 2017 October 7 and 31, in Green Bank, West Virginia, USA, under stable atmospheric conditions during both night and day hours. The observing procedure and data reduction are identical to those presented in Harrington et al. (2018) and Dannerbauer et al. (2019), and we briefly describe the procedure below. We executed a SubBeamNod observing mode, with 4 minutes of integration per scan. Each session started with a pointing and focus check, followed by a pointing every 1–1.5 hr. Focus measurements were conducted every 3 hr for longer observing sessions. We tuned the back-end spectrometer, VEGAS, to its low-resolution, 1.5 GHz bandwidth mode. Using GBTIDL (Marganian et al. 2013), we computed all On-Off measurements and corrected for atmospheric attenuation. Each spectrum was inspected by eye after baseline subtraction (see Harrington et al. 2018), and roughly 10%–15% of scans were dropped. After subtracting a baseline and then averaging, we smoothed the spectra to ∼100 km s−1 channel resolution.
We observed mid- to high-J CO and [C i] emission lines in the sources available in the Southern Hemisphere using both the PI230 and dual-frequency FLASH+ 345/460L receivers on the APEX telescope in San Pedro de Atacama, Chile (Güsten et al. 2006). We used Max Planck Society observing time between 2018 May 22 and September 28 (Pr. M-0101.F-9503A-2018; PI: Harrington), soon after the new telescope surface was installed and commissioned. Observations took place in a range of very good to reasonable weather conditions, i.e., precipitable water vapor (PWV) ∼ 2–3 mm for PI230 and PWV < 2 mm for FLASH+. FLASH (Heyminck et al. 2006) is a two-sideband (SB) dual-frequency heterodyne receiver with a single orthogonal linear polarization for each of the 345 and 460 GHz atmospheric windows. Both the FLASH 345/460 channels have an upper and lower SB with 4 GHz bandwidth. The PI230 receiver is a two-SB heterodyne receiver with a dual-polarization capability and 2 × 8 GHz bandwidth. We used a standard wobbler switching with a chopping rate of 1.5 Hz and an azimuthal throw offset of 30''. Each scan consisted of a hot/sky/cold calibration 600'' off-source, followed by 12 subscans of 20 s per on-source integration time. Focus checks were performed roughly every 3–4 hr, whereas pointing checks on Jupiter or a nearby star were performed every 1–2 hr (pointing accuracy within 2''–3''). All data were recorded using the MPIfR eXtended bandwidth Fast Fourier Transform spectrometers (FFTS; Klein et al. 2006), and each of the scans was reduced and analyzed using the CLASS and GREG packages within the GILDAS25 software (Pety 2005). The spectrum from each scan was smoothed to ∼100 km s−1 channel resolution and assessed after subtracting a first-order baseline from the emission-line-free channels. The baseline stability depends strongly on the observed frequency and/or weather conditions; therefore, we dropped 10%–25% of the scans before co-adding the baseline-subtracted, rms-weighted spectrum.
We observed low- to high-J CO and [C i] emission lines with the IRAM 30 m telescope during three observing semesters (Pr. 187-16, 170-17, 201-18; PI: K. Harrington), between 2017 January 29 and 2019 April 24. Overall, weather conditions varied from excellent to poor, with the reference zenith opacity at 225 GHz, τν225 GHz ∼ 0.05–0.8. We utilized all four of the EMIR receivers (Carter et al. 2012), E090, E150, E230, and E330, often with dual tuning modes to target more than one CO/[C i] emission line. In total, the EMIR receiver has a dual polarization, with a 16 GHz bandwidth back-end spectrometer, the fast Fourier Transform Spectrometre (FTS200), and an 8 GHz bandwidth spectrometer, the WIde-band Line Multiple Auto-correlator (WILMA). The FTS200 has a finer channel resolution; however, it is subject to baseline instabilities such as platforming features in the bandpass. The WILMA has a lower native channel resolution and was used almost always alongside the FTS200 to verify observed line features. We carried out a standard wobbler switching observing mode with offset throws of 40'' every second. Each wobbler switching mode procedure includes three 5-minute integrations (i.e., 12 25 s subscans). Pointing corrections were performed (e.g., Uranus, Venus, J1226+023, J1418+546) every 1–2 hr, with azimuth and elevation pointing offsets typically within 1''–3''. Focus measurements were repeated roughly 1.5 hr after sunset/sunrise and every 3–4 hr to correct for thermal deformations of the primary dish and/or secondary mirror. In the same manner presented in Harrington et al. (2019), all scans were reduced using the GILDAS package,26 smoothed to ∼50–150 km s−1 channel resolution, followed by a visual inspection of a baseline-subtracted spectrum and subsequent averaging of the rms-weighted spectrum. We dropped 5%–20% of the scans per line owing to unstable baselines or noise spikes, which may strongly depend on the specific tuning setup and weather.
3.2. Absolute Calibration Errors
In the following analyses we model the apparent (not corrected for lens magnification) velocity-integrated flux density, integrated across the entire line profile. We apply a total error based on the typical systematic uncertainties associated with pointed single-dish spectroscopic observations. These include atmospheric instabilities (transmission varying on the order of seconds/minutes), pointing/focus corrections, baseline subtraction procedures, the calibration of the Jy K−1 gain conversion, and receiver stability across the entire bandpass. For all CO (1−0) lines, we adopt a 25% uncertainty for systematic effects with the GBT (see Frayer et al. 2018; Harrington et al. 2018). We adopt a 20% uncertainty for all APEX and IRAM 30 m measurements less than ∼240 GHz and a 35% uncertainty for lines observed at higher frequencies. We add an additional 5%–10% total uncertainty to those emission lines that were detected at the edge of the EMIR receiver capabilities and at lower atmospheric transmission. Despite careful pointing/focus/calibration measurements, we add an additional 5% total uncertainty to all integrated fluxes used in this study owing to the heterogeneous observing conditions among all of the emission lines observed or reported in other studies. Sources LPsJ1322, LPsJ0846, and LPsJ0748 have extended emission as detected by AzTEC 1.1 mm continuum (D. Berman et al. 2021, in preparation). Therefore, we measured the emission surrounding the reported R.A./decl., which we consider to be representative of the entire galaxy. As noted in D. Berman et al. (2021, in preparation) for LPsJ1322, the ALMA measurements did not account for ∼35% of the LMT/AzTEC 1.1 mm continuum flux owing to its large Einstein ring (see also Tables 1 and 2). Therefore, we have adopted an additional 35% total error for the lines in this source. High-frequency measurements may underestimate the total flux for the most extended LPs owing to smaller beam sizes and pointing errors. The conservative total uncertainties we adopt for these single-dish measurements thereby include a wide variation in the value of the flux density in an attempt to constrain the average global ISM properties.
4. Emission-line Profiles
Figure 1 shows an example set of low- to high-J CO and [C i] line detections for LPsJ1323. The remaining figures for the line spectra for the LPs can be accessed online in the supplemental journal. In all of the 21/24 LPs with a [C i] line detection, the emission-line profile matches that of the spectrally adjacent CO emission. Specific examples of this can be seen in the [C i] (2−1)/CO (7−6) spectrally adjacent pair (see, e.g., LPsJ0116, LPsJ0209, LPsJ0305, LPsJ0748, LPsJ1326). Most of the CO and [C i] lines have similar line widths and shape. These spectrally resolved measurements indicate that the emitting regions follow the same large-scale dynamics, based on these spatially unresolved measurements.
Figure 1.
Apparent flux density vs. velocity for the CO and [C i] line detections. The best-fit models of all line and continuum data are shown for LPsJ1323 in Figure 4. The CO (1−0) line was previously presented in Harrington et al. (2018). Spectra and best-fit models for the other LPs can be accessed online. (The complete figure set (24 images) is available.)
Download figure:
Standard image High-resolution imageFigure 2 shows the measured velocity-integrated line fluxes, as reported in Table 7, compared to our literature compilation (including Carilli & Walter 2013; Cañameras et al. 2015; Yang et al. 2017; Kirkpatrick et al. 2019). Many CO line measurements have now probed more than 2–3 orders of magnitude in the observed velocity-integrated line flux densities across this large sample of ∼270 galaxies at z ∼ 1–7. The LPs are among the brightest CO sources on the sky, due to the magnification effects of strong lensing.
Figure 2. Velocity-integrated flux density (log scale) measurements plotted vs. the CO rotational quantum number, Jup, for the LPs (red diamond). The black circles show the LPs and K19 z ∼ 1–7 sample, described in Section 4.
Download figure:
Standard image High-resolution imageTo characterize the velocity-integrated flux density, we calculate the full line width at zero intensity (FWZI) for all of the measured line fluxes in Table 7. We note that neither do all spectra have similar line shapes between the sample of LPs nor are all of the lines resolved at relatively high velocity resolution (e.g., 20–50 km s−1), so we therefore avoid fitting simple 1D Gaussian models to analyze the line profiles. The mean and standard deviation of the FWZI for all of the CO lines for the entire sample of LPs is 851 ± 183 km s−1. In Figure 3, the FWZI is normalized to the FWZI of the CO (3−2) line to examine whether the line profiles may change as a function of Jup. The average value of this normalized FWZI decreases with increasing Jup, although the large total uncertainties for the lines do not reveal a statistically significant trend. The LPs with detections of higher-J CO lines show a similar line profile to that seen in the emission lines of the lower-J rotational transitions. In some cases the FWZI of the high-J emission lines is narrower than the lower-J emission-line profiles at comparable velocity resolution. This is apparent in LPsJ1336, as the CO (1–0; 5–4; 6–5; 8–7; 9–8; 10–9) emission lines have a comparable FWZI, whereas the strong detection of the CO (11−10) line reveals an FWZI that is roughly half. Narrow-line emission in the highest-J lines, compared to the lower-J lines, is observed in LPsJ0116, LPsJ0226, LPsJ1202, and LPsJ1544. This is not seen in other systems with such high-J measurements. In 3/24 LPs with large lensing arcs, pointed observations may only partially cover the entire emitting region. Therefore, the observed emission is assumed to be representative of the galaxy-scale ISM of the lensed galaxy. In these cases, additional uncertainties have been added to the observed integrated line fluxes (Section 3.2).
Figure 3. Apparent velocity-integrated flux density measurements plotted vs. the CO rotational quantum number, Jup, for the LPs (red diamonds).
Download figure:
Standard image High-resolution imageThe lens magnification factor, μL, may have a different value for the low- and high-J CO lines and thus may yield a potential differential lensing effect (see Appendix A). Differential lensing of the diffuse and dense molecular gas traced by [C i] and CO may be negligible in most, if not all, of the LPs, as the line profiles would have shown strong variations across the spectrally resolved line profiles. Since the average, normalized FWZI drops slightly (10%–25%) from the median value for the higher-J lines, such a change is not statistically significant given error uncertainties. Therefore, we are confident that differential lensing effects do not impact the general trends we present. The strong asymmetric lines may indicate27 different magnification factors across the line profile (Leung et al. 2017), while the dust and CO may be slightly offset in the source plane (Rivera et al. 2019). These values will likely be the same for both the [C i] and CO lines, as the overall line shapes are similar. We discuss differential lensing in greater detail in Appendix A, and we briefly note that Cañameras et al. (2018b) report a 5%–10% difference in the flux-weighted mean magnification factor derived for the low-J CO and millimeter dust continuum, respectively, for 5/24 LPs presented in this work. For 2/24 LPs in this work, Cañameras et al. (2018b) reported less than 30% differential lensing of the dust and low-J CO. We are unable to de-magnify the sources for the analyses presented in this work, since a magnification factor for different lines does not exist. Some lensed SPT-selected galaxies have a noted range from negligible differences in the magnification for different CO line transitions, up to a factor of two (Apostolovski et al. 2019; Dong et al. 2019).
5. Simultaneous Modeling of Line and Continuum Emission
We utilize two state-of-the-art radiative transfer codes to simultaneously model both the observed line fluxes and measurements of the thermal dust continuum emission. This enables us to study the gas excitation conditions for the LPs using (i) a widely used approach to model two molecular gas components and (ii) a more realistic molecular ISM with a turbulence-driven, lognormal density distribution for the gas density. The models we use are primarily derived from the equations presented in Weiß et al (2007). For the analyses in this work, the primary modification to those models is that the gas and dust are now modeled simultaneously. Below we summarize the main properties of these modeling tools. A future work will enclose all of the details for the models. We will first describe the model that considers two gas components. Afterward we will summarize the second model, which includes many of the same input parameters as the first model, despite being a more physically motivated, modified version.
5.1. The 2-component Model Parameters
Our first model is a simple non-LTE radiative transfer model, referred to as the "2-component" model. This model can, in principle, take into account an arbitrary number of molecular gas components. Nonetheless, due to the large number of coupled parameters and model degeneracies, we consider only two gas components, each with a unique, constant density. In Table 3 we summarize the range in parameter space we explore for both models. We consider 14 free parameters for the 2-component model. Each of the two gas components in the 2-component model has seven free parameters: log( ) (base 10), Tkin, ΔVturb, κvir,
) (base 10), Tkin, ΔVturb, κvir,  , [C i]/H2, and Tkin/Td. We have specifically restricted the values of the other modeled parameters, i.e.,
, [C i]/H2, and Tkin/Td. We have specifically restricted the values of the other modeled parameters, i.e.,  , CO/H2, GDMR. The last two parameters limit our investigation to solar-metallicity environments, as described below.
, CO/H2, GDMR. The last two parameters limit our investigation to solar-metallicity environments, as described below.
Table 3. Parameter Space
log10 (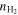 ) ) |
Tkin | Tkin/Tdust | μReff | ΔV | κvir | GDMR | CO/H2 | [C i]/H2 |
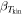
|
![${\beta }_{[{\rm{C}}{\rm\small{I}}]/{{\rm{H}}}_{2}}$](https://content.cld.iop.org/journals/0004-637X/908/1/95/revision1/apjabcc01ieqn24.gif)
|
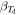
|
|---|---|---|---|---|---|---|---|---|---|---|---|
| (cm−3) | (K) | (pc) | (km s−1) | (km s−1 pc−1 cm3/2) | |||||||
| 1–7 | 15–600 | 0.5–6.0 | 0.1-19999 | 10–200 | 1.0-3.0 | 120–150 | 1 × 10−4–2 × 10−4 | 1 × 10−5–2 × 10−4 | ⋯ | ⋯ | 1.8–2.0 |
| 1–7 | 15–600 | 0.5–6.0 | 0.1-19999 | 10–200 | 1.0–3.0 | 120–150 | 1 × 10−4–2 × 10−4 | 1 × 10−5–2 × 10−4 | −0.5–0.05 | −5.0–0.0 | 1.8–2.0 |
Note. The ranges in parameter space we explore in both models.
Download table as: ASCIITypeset image
Effective radius: We parameterize the size of the emitting region by an effective radius that defines the apparent source solid angle  (e.g., Weiß et al 2007), using the angular diameter distance, Dang, the magnification factor of the observed intensity, μL, and the apparent effective radius of the emission region,
(e.g., Weiß et al 2007), using the angular diameter distance, Dang, the magnification factor of the observed intensity, μL, and the apparent effective radius of the emission region,  . This apparent, effective disk radius would be equivalent to the intrinsic emitting region if the emission came from a filled aperture for an unlensed, face-on, circular disk (Weiß et al 2007). It is therefore a minimum radius, as the emission may come from an unfilled aperture, which may be more widely distributed.
. This apparent, effective disk radius would be equivalent to the intrinsic emitting region if the emission came from a filled aperture for an unlensed, face-on, circular disk (Weiß et al 2007). It is therefore a minimum radius, as the emission may come from an unfilled aperture, which may be more widely distributed.
Molecular gas density and gas/dust temperatures: For each gas component, we consider a range of molecular gas densities of log( ) = 1–7 cm−3. We probe gas kinetic temperatures, Tkin, ranging between the redshifted CMB radiation temperature and 600 K (corresponding to the highest-energy CO transition we model, Jup = 15). We account for the possible decoupling of the gas and dust by setting a limit on the gas kinetic temperature, as
) = 1–7 cm−3. We probe gas kinetic temperatures, Tkin, ranging between the redshifted CMB radiation temperature and 600 K (corresponding to the highest-energy CO transition we model, Jup = 15). We account for the possible decoupling of the gas and dust by setting a limit on the gas kinetic temperature, as  . The range we explore for this ratio of the gas kinetic temperature to the dust temperature (Tkin/Td = 0.5–6) is in agreement with theoretical work (see the review by Krumholz 2014). In well-shielded regions that have log(
. The range we explore for this ratio of the gas kinetic temperature to the dust temperature (Tkin/Td = 0.5–6) is in agreement with theoretical work (see the review by Krumholz 2014). In well-shielded regions that have log( ) > 4.5 cm−3 the molecular gas and dust may have a stronger coupling than in lower-density environments. According to Krumholz (2014), within gas densities of log(
) > 4.5 cm−3 the molecular gas and dust may have a stronger coupling than in lower-density environments. According to Krumholz (2014), within gas densities of log( ) > 6 cm−3 the gas and dust temperatures are expected to be nearly equivalent. We do not implement an explicit relationship between Tkin/Td and the gas density. We note that we simply solve for the gas kinetic temperature and dust temperature without modeling any specific heating mechanism. We note that theoretical and observational studies suggest that the overall molecular ISM of a starburst/AGN galaxy could also be influenced by cosmic rays or X-rays (e.g., Meijerink et al. 2007), and these heating mechanisms may be influential in determining the value we derive for the gas kinetic temperature.
) > 6 cm−3 the gas and dust temperatures are expected to be nearly equivalent. We do not implement an explicit relationship between Tkin/Td and the gas density. We note that we simply solve for the gas kinetic temperature and dust temperature without modeling any specific heating mechanism. We note that theoretical and observational studies suggest that the overall molecular ISM of a starburst/AGN galaxy could also be influenced by cosmic rays or X-rays (e.g., Meijerink et al. 2007), and these heating mechanisms may be influential in determining the value we derive for the gas kinetic temperature.
Velocity gradient and turbulent velocity dispersion: The velocity gradient, δv/δr, and the molecular gas density together define dynamically bound or unbound systems, parameterized by the virial parameter, κvir. The κvir parameter defines the relationship between turbulent and gravitational energy and relates the velocity gradient and H2 gas volume density (see Equation (2) of Goldsmith 2001). We explore a range corresponding to a physically bound molecular medium, up to a marginally unbound system, with κvir = 1–3 (Greve et al. 2009; Papadopoulos et al. 2012a). The ΔVturb parameter is the turbulent velocity dispersion for each component in the 2-component model calculations and is also, by definition, a mathematical term required for dimensional homogeneity.
Gas-phase abundances, metallicity, and gas-to-dust mass ratio: We leave the carbon abundance as a free parameter, probing ranges consistent with diffuse to dense giant molecular cloud (GMC) abundances of [C i]/H2 = 1 × 10−5–2 × 10−4. The wide range in [C i]/H2 reflects the chemistry in the dense gas. There is an expected decrease in the value of the carbon abundance for increasing molecular gas density, as chemical network calculations show that atomic carbon quickly disappears from the gas phase and is transformed into other molecules (see, e.g., Hollenbach & Tielens 1999; Glover & Clark 2012; Goldbaum et al. 2016). We assume an average Galactic disk value for the CO gas-phase abundance in the range of CO/H2 = (1–2) × 10−4 to be consistent with the typical molecular abundance of giant molecular clouds in the Milky Way (Scoville & Young 1983; Wilson et al. 1986; Blake et al. 1987). Instead of allowing the gas-to-dust mass ratio parameter to range freely, we restrict this to a value of GDMR = 120–150 (Draine 2011), i.e., consistent with the observed value in the Milky Way (Draine 2011). Recent studies (Casey et al. 2014, and references therein) suggest that massive star-forming galaxies represent high-density cosmic regions at z = 1–3. The fiducial solar-metallicity, Milky Way–type values are supported by our selection criteria to study extremely dusty star-forming galaxies with sufficient metal enrichment at high z. We may therefore expect the LPs to have already accumulated at least a near-solar metallicity in a relatively short amount of time (Cen & Ostriker 1999; Bothwell et al. 2016). Some derived quantities, such as the GDMR and the α conversion factor, will depend on metallicity (Narayanan et al. 2012). For galaxies with 2–3× solar metallicity, the total gas mass comparisons would be impacted by a relative linear decrease in both the GDMR and overall gas mass estimates from [C i] and CO.
5.2. Computing the Line and Continuum Fluxes
We model the line fluxes of the CO (1−0) to CO (15–14) transitions, corresponding to upper-state energy levels Eu = 5.5–663.4 K. We use the collisional rate coefficients from Flower & Pineau des Forêts (2001) to solve for the balance of excitation and de-excitation from and to a given energy state. To compute the CO (and C i if detected) level populations, it is important to take the continuum radiation fields into account. We include (i) the CMB radiation at the respective redshift, with  K, and (ii) the IR radiation field.
K, and (ii) the IR radiation field.
The apparent line flux densities, μLSCO/[C i], are directly proportional to the physical apparent source solid angle and line brightness temperatures, Tb. In the non-LTE, LVG framework we calculate the full radiative description of the Tb, although it is classically defined by its equivalent representation on the Rayleigh–Jeans side of the emitting spectrum, i.e., hνobs ≪ kTb. The values of Tb we compute depend on the gas volume density, the kinetic temperature, and the gas-phase abundance per velocity gradient in the LVG description. Altogether, the values of Tb are used to model the observed line fluxes:
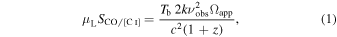
with c the speed of light, z the redshift, νobs the observed frequency of the CO or [C i] line, and k the Boltzmann constant.
We parameterize the observed dust continuum radiation field by the dust temperature, Td, dust emissivity index,  , apparent dust mass, and source solid angle. The last three parameters also characterize the wavelength at which the dust opacity becomes unity, λ0.28
We note that λ0 is not a free parameter in our model but can be computed from the apparent dust mass and source solid angle via Equation (2). For simplicity, we restrict the
, apparent dust mass, and source solid angle. The last three parameters also characterize the wavelength at which the dust opacity becomes unity, λ0.28
We note that λ0 is not a free parameter in our model but can be computed from the apparent dust mass and source solid angle via Equation (2). For simplicity, we restrict the  to a value in the range of
to a value in the range of  in both models to be consistent with previous studies of the LPs (Cañameras et al. 2015; Harrington et al. 2016). These values are also in agreement with the Milky Way average (Planck Collaboration et al. 2011) and other studies of local and high-redshift star-forming galaxies (Casey et al. 2014).29
in both models to be consistent with previous studies of the LPs (Cañameras et al. 2015; Harrington et al. 2016). These values are also in agreement with the Milky Way average (Planck Collaboration et al. 2011) and other studies of local and high-redshift star-forming galaxies (Casey et al. 2014).29
We then compute the full radiative transfer analysis for the two components in the 2-component model to derive both the dust opacity and line opacities in each calculation. The larger component can overlap with the more compact component, and we therefore take into account this difference when computing the overall dust SED (see, e.g., Downes & Eckart 2007). We keep the same frequency-dependent dust emissivity index,  , for each component. The dust optical depth is calculated using Equations (2) and (3) of Weiß et al (2007), assuming a frequency-dependent dust mass absorption coefficient, κd [cm2 g−1] (Kruegel & Siebenmorgen 1994), yielding
, for each component. The dust optical depth is calculated using Equations (2) and (3) of Weiß et al (2007), assuming a frequency-dependent dust mass absorption coefficient, κd [cm2 g−1] (Kruegel & Siebenmorgen 1994), yielding
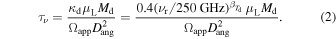
We connect the modeled line and continuum fluxes by using the derived dust opacity and inferred CO (or [C i]) gas column density to calculate the H2 gas column density, using Equation (7) of Weiß et al (2007). The GDMR parameter is ultimately used to link the overall line fluxes and dust continuum in a self-consistent manner. We recall that the Tkin/Td parameter also links the line and continuum emission properties. We applied a prior for some of the LPs (see best-fit model plots in the supplemental figures), with dust photometry limited mostly to Planck measurements, so that the dust SED turns over beyond rest-frame flux densities of  (i.e., rest-frame ∼50 μm for the z ∼ 2–3 LPs). This is in agreement with the physical conditions with which our model is sensitive to, i.e., the rest-frame FIR to millimeter wavelengths—rather than near- and mid-IR wavelengths. This restriction also prevents a largely unconstrained (and also unphysical) solution space, with extremely high apparent FIR luminosity (
(i.e., rest-frame ∼50 μm for the z ∼ 2–3 LPs). This is in agreement with the physical conditions with which our model is sensitive to, i.e., the rest-frame FIR to millimeter wavelengths—rather than near- and mid-IR wavelengths. This restriction also prevents a largely unconstrained (and also unphysical) solution space, with extremely high apparent FIR luminosity ( L⊙).30
Note that dusty high-z star-forming galaxies, with full coverage of their thermal dust SED, fully support this prior (Strandet et al. 2016).
L⊙).30
Note that dusty high-z star-forming galaxies, with full coverage of their thermal dust SED, fully support this prior (Strandet et al. 2016).
5.3. The Turbulence Model Parameters
The second model, hereafter the "Turbulence" model, is more sophisticated in describing the molecular ISM. It has nine free parameters and is represented as a single gas component described by a gas density pdf. We also model the line and continuum emission simultaneously in this model, including all of the same input parameters. For the Turbulence model, the effective radius connects the source solid angle to the gas density pdf, which makes this model distinct from the 2-component model. In contrast, the 2-component model simply treats the gas density and the source solid angle as completely independent parameters and also does not draw an explicit connection between the gas density and gas kinetic temperature.
We explore a broad range of values for the H2 gas volume density in the Turbulence model, log( ) = 1–10 cm−3, with a restricted range for the mean density of the density pdf to values of log(
) = 1–10 cm−3, with a restricted range for the mean density of the density pdf to values of log( ) = 1–7 cm−3. The mean molecular gas density thereby determines the other model parameter to describe the global mean ISM properties of the LPs. We sample the best-fit, minimum-χ2 Turbulence model density pdf by 50 bins. Each of the 50 gas densities is proportional to a solid angle that is occupied by that specific density bin. Therefore, each density corresponds to a radius—such that the sum of all areas is normalized to the input source solid angle. This implies that the model fit values for the dust and line SEDs are the sum of 50 individual LVG calculations that have used the value for each of those densities to calculate the relative emission properties. These altogether sum to the total line and continuum emission that has been measured.
) = 1–7 cm−3. The mean molecular gas density thereby determines the other model parameter to describe the global mean ISM properties of the LPs. We sample the best-fit, minimum-χ2 Turbulence model density pdf by 50 bins. Each of the 50 gas densities is proportional to a solid angle that is occupied by that specific density bin. Therefore, each density corresponds to a radius—such that the sum of all areas is normalized to the input source solid angle. This implies that the model fit values for the dust and line SEDs are the sum of 50 individual LVG calculations that have used the value for each of those densities to calculate the relative emission properties. These altogether sum to the total line and continuum emission that has been measured.
There are two unique parameters for the Turbulence model, ![${\beta }_{[{\rm{C}}{\rm\small{I}}]}$](https://content.cld.iop.org/journals/0004-637X/908/1/95/revision1/apjabcc01ieqn42.gif) and
and  . The power-law index,
. The power-law index, ![${\beta }_{[{\rm{C}}{\rm\small{I}}]}$](https://content.cld.iop.org/journals/0004-637X/908/1/95/revision1/apjabcc01ieqn44.gif) , constrains the value of the carbon abundance relative to [C i]/H2 (Weiß et al. 2003). We express
, constrains the value of the carbon abundance relative to [C i]/H2 (Weiß et al. 2003). We express ![${\beta }_{[{\rm{C}}{\rm\small{I}}]}$](https://content.cld.iop.org/journals/0004-637X/908/1/95/revision1/apjabcc01ieqn45.gif) as a power law of the density. We further explore this parameter in Section 6.3. The
as a power law of the density. We further explore this parameter in Section 6.3. The  parameter couples the gas kinetic temperature to the gas volume density by a power-law index,
parameter couples the gas kinetic temperature to the gas volume density by a power-law index,  , as Tkin ∝ log(
, as Tkin ∝ log( )
)  , such that the more diffuse gas tends to have higher gas kinetic temperatures. This functional behavior has been well studied in magnetohydrodynamical simulations (Krumholz 2014). The modeled galaxy-wide turbulent velocity dispersion, ΔVturb, is a free parameter in the Turbulence model. Although similar to the 2-component model, here it determines the width of the lognormal gas density pdf that is centered on the mean molecular gas density.
, such that the more diffuse gas tends to have higher gas kinetic temperatures. This functional behavior has been well studied in magnetohydrodynamical simulations (Krumholz 2014). The modeled galaxy-wide turbulent velocity dispersion, ΔVturb, is a free parameter in the Turbulence model. Although similar to the 2-component model, here it determines the width of the lognormal gas density pdf that is centered on the mean molecular gas density.
5.4. Fitting
We use the parameter ranges in Table 3 to model the observed data using a bee algorithm optimization procedure (Pham & Castellani 2009), as used in Strandet et al. (2017). In this optimization procedure, each model iteration attempts to solve for the observed data by exploring a number of model calculations (hereafter "bees") based on the free parameters. These "bees" have a random initialization within the defined parameter space and record the model parameters with the best reduced χ2 value, as determined by the dust, CO, and [C i] data. The parameter space is further explored by "bees" that provide a fine sampling around the best χ2 regions, while other "bees" continue to evaluate the parameter space randomly to avoid being trapped in a local minimum during each iteration. We evaluate ∼105 models in each modeling procedure (for either the 2-component or Turbulence model). To avoid repeatedly obtaining the same best-fit, minimum-χ2 values, and also to avoid remaining fixed in a narrow solution space within the posterior probability distribution of each parameter, we regenerate this entire procedure multiple times, resulting in ∼2 million model evaluations per galaxy for each of the 2-component or Turbulence models. To describe the mean, global gas excitation conditions of the LPs, we refer primarily to the mean quantities and the standard deviation for the sample (Table 5). The quantities presented in Table 5 are based on the total χ2-weighted mean parameter values for each of the individual LPs, as evaluated for each parameter value from the ∼2 million models. The general trends and conclusions are not affected by the choice of the total χ2-weighted mean and standard deviation of the global properties we derive, as opposed to, e.g., the median (50th percentile) values. Since we present the modeling of spatially unresolved, galaxy-integrated measurements, with large absolute calibration errors (Section 3.2), we adopt this mean quantity to reflect the average galaxy-wide properties based on the limitations of our data.
6. Model Results
The best-fit, minimum-χ2 model plots for all of the LPs can be accessed online (see also Appendix C). We show an example below, for LPsJ1323 (Figure 4), for the best-fit model values for the dust SED, CO spectral line energy distribution (line SED), and both ground-state [C i] velocity-integrated line fluxes. For the dust SED and CO line SEDs in the Turbulence model we also plot the relative contribution from each of the density bins in the pdf. To facilitate comparison to the total observed best-fit model, we arbitrarily increase the y-axis value for each density component to scale the individual LVG calculations. These calculations, representative of different densities sampling the gas density pdf, are shown in different colors to visualize which mean density dominates the observed intensities. The accompanying figure for the best-fit 2-component model shows the true y-axis values for the relative contributions from component one and component two—which add to the total observed data points.
Figure 4.
Best-fit, minimum-χ2 model solution for LPsJ1323. Top: Turbulence model for the dust SED, CO, and [C i] velocity-integrated line fluxes as determined by the best χ2. For clarity, different dashed colored curves denote the representative contributions to the density pdf for the molecular gas densities of log( ) = 2 (yellow), 3 (blue), 4 (purple), 5 (green), and 6 (pink) cm−3. The gray dashed lines represent the remaining LVG calculations (from the 50 total samples) that sample the gas density pdf (see Section 5). For the Turbulence model, these individual density contributions have a y-axis scaled by a factor of 5 for both the dust and line SED to facilitate interpretation of the dominant gas density. All observed data are shown as red diamonds. The best-fit [C i] line fluxes are plotted over the observed data. All solid red lines indicate the total best-fit, minimum-χ2 model. Bottom: 2-component model curves for the lower-excitation component (black dotted) and higher-excitation component (black dashed). The best-fit [C i] line fluxes from the lower-excitation component and higher-excitation component are denoted by a downward-pointing and upward-pointing gray triangle, respectively. (The complete figure set (24 images) is available.)
) = 2 (yellow), 3 (blue), 4 (purple), 5 (green), and 6 (pink) cm−3. The gray dashed lines represent the remaining LVG calculations (from the 50 total samples) that sample the gas density pdf (see Section 5). For the Turbulence model, these individual density contributions have a y-axis scaled by a factor of 5 for both the dust and line SED to facilitate interpretation of the dominant gas density. All observed data are shown as red diamonds. The best-fit [C i] line fluxes are plotted over the observed data. All solid red lines indicate the total best-fit, minimum-χ2 model. Bottom: 2-component model curves for the lower-excitation component (black dotted) and higher-excitation component (black dashed). The best-fit [C i] line fluxes from the lower-excitation component and higher-excitation component are denoted by a downward-pointing and upward-pointing gray triangle, respectively. (The complete figure set (24 images) is available.)
Download figure:
Standard image High-resolution image6.1. CO Line SEDs
The majority of the LPs show a broad peak in the CO line SED at Jup = 4–6. The observed dust emission arises from molecular gas with log( ) = 2–3 cm−3, while the observed CO excitation ladders are dominated by log(
) = 2–3 cm−3, while the observed CO excitation ladders are dominated by log( ) = 3–4 cm−3. There is sustained CO excitation out to Jup = 9–11 in most of the LPs. For this emission, molecular gas with log(
) = 3–4 cm−3. There is sustained CO excitation out to Jup = 9–11 in most of the LPs. For this emission, molecular gas with log( ) = 4–5 cm−3 is dominant (see, e.g., LPsJ0209, LPsJ1329, LPsJ1138).
) = 4–5 cm−3 is dominant (see, e.g., LPsJ0209, LPsJ1329, LPsJ1138).
To examine the dispersion in gas excitation conditions, Figure 5 shows all of the best-fit, minimum-χ2 Turbulence model-derived CO velocity-integrated line fluxes, normalized by the sum of all Jup = 1–15 velocity-integrated line fluxes. This normalization indicates the relative strength between various line transitions among the sample, and we will present a more quantitative classification of the broad range in gas excitation conditions in Section 7.1.1. Using the velocity-integrated line fluxes, we can calculate the line luminosity of CO or [C i] in terms of the area-integrated line surface brightness, ![${L}_{\mathrm{CO}/[{\rm{C}}\,{\rm\small{I}}]}^{{\prime} }$](https://content.cld.iop.org/journals/0004-637X/908/1/95/revision1/apjabcc01ieqn54.gif) . We calculate this value using the standard equations presented in Solomon et al. (1997). The ratio of this value for any two CO transitions will provide an average estimate of the intrinsic brightness temperature (Tb) ratio within the CO-emitting gas. For the two lowest rotational transitions, this ratio is often close to unity for active star-forming systems (Carilli & Walter 2013), assuming that the two lines have the same spatial extent on average with the same Tb, such that the two lines are thermalized. Table 4 shows the best-fit, minimum-χ2 model-derived line ratios from our physically motivated Turbulence model, yielding systematically derived values for the brightness temperature ratios corresponding to the ratio of
. We calculate this value using the standard equations presented in Solomon et al. (1997). The ratio of this value for any two CO transitions will provide an average estimate of the intrinsic brightness temperature (Tb) ratio within the CO-emitting gas. For the two lowest rotational transitions, this ratio is often close to unity for active star-forming systems (Carilli & Walter 2013), assuming that the two lines have the same spatial extent on average with the same Tb, such that the two lines are thermalized. Table 4 shows the best-fit, minimum-χ2 model-derived line ratios from our physically motivated Turbulence model, yielding systematically derived values for the brightness temperature ratios corresponding to the ratio of  /
/ , denoted as
, denoted as  . Table 4 summarizes the mean and standard deviation of the LP sample from these best-fit, minimum-χ2 Turbulence models, and we will discuss Table 4 in more detail in Section 7.1.2.
. Table 4 summarizes the mean and standard deviation of the LP sample from these best-fit, minimum-χ2 Turbulence models, and we will discuss Table 4 in more detail in Section 7.1.2.
Figure 5. Best-fit, minimum-χ2 Turbulence models for the CO velocity-integrated line fluxes, normalized by the sum of all Jup = 1–15 velocity-integrated line fluxes, for all of the LPs.
Download figure:
Standard image High-resolution imageTable 4. Line Brightness Temperature Ratios
| Jup | LPs | LPs and K19 | K19 "All Sources" | CW13 SMGs | CW13 QSOs |
|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 | 1 |
| 2 | 0.88 ± 0.07 | 0.73 ± 0.10 | 0.78 ± 0.13 | 0.85 | 0.99 |
| 3 | 0.69 ± 0.12 | 0.75 ± 0.11 | 0.78 ± 0.14 | 0.66 | 0.97 |
| 4 | 0.52 ± 0.14 | 0.46 ± 0.07 | 0.49 ± 0.10 | 0.46 | 0.87 |
| 5 | 0.37 ± 0.15 | 0.36 ± 0.06 | 0.34 ± 0.07 | 0.39 | 0.69 |
| 6 | 0.25 ± 0.14 | 0.28 ± 0.04 | 0.31 ± 0.06 | ⋯ | ⋯ |
| 7 | 0.17 ± 0.12 | 0.18 ± 0.03 | 0.21 ± 0.04 | ⋯ | ⋯ |
| 8 | 0.11 ± 0.09 | 0.08 ± 0.02 | 0.11 ± 0.03 | ⋯ | ⋯ |
| 9 | 0.07 ± 0.07 | 0.07 ± 0.02 | 0.14 ± 0.04 | ⋯ | ⋯ |
| 10 | 0.04 ± 0.05 | 0.07 ± 0.02 | 0.08 ± 0.04 | ⋯ | ⋯ |
| 11 | 0.02 ± 0.02 | 0.05 ± 0.02 | 0.12 ± 0.03 | ⋯ | ⋯ |
| 12 | 0.02 ± 0.03 | 0.02 ± 0.01 | ⋯ | ⋯ | ⋯ |
Note. Mean and 1σ standard deviation of the line brightness temperature ratios among the sample of 24 LPs based on the best-fit, minimum-χ2 Turbulence models. The LPs and K19 sample catalog of all observed CO lines, in ∼270 z ∼ 1–7 galaxies, is used to derive the median line ratios, as described in Section 7.1.2. The "All Sources" (z = 1–7) sample consists of heterogenously selected galaxies with CO line detections (Kirkpatrick et al. 2019). The quoted values in the last two columns are from Carilli & Walter (2013) for the average values for both high-z (sub)millimeter bright CO emitters (SMGs) and quasars (QSOs).
Download table as: ASCIITypeset image
6.2. Physical Gas Properties of the LPs
6.2.1. CO and [C i] Line Opacities
We now focus on the best-fit values for the CO and [C i] line opacities, as derived in the 2-component model. In the LVG approximation, we consider an emitting region of gas that is excited owing to both the collisional interactions and the external radiation field. The observed line fluxes are computed using the line opacities, τ, and the standard LVG assumption of the escape probability method formalism, which defines the probability of a photon escaping or entering the medium. As noted in other studies (Scoville & Solomon 1974), this probability is proportional to  .
.
The observed line and continuum fluxes are determined by the relevant gas-phase abundance(s), volume density, and molecular gas kinetic temperature (i.e., the Maxwellian velocity distribution). Overall, these effects shape the value of the line opacity, specifically as

where "N(mol)" is, here, the CO or [C i] gas column density, ΔVturb is the galaxy-wide turbulent velocity, δv/δr is the large-scale, systemic velocity gradient of the molecular/atomic gas, and " " is the H2 gas volume density.
" is the H2 gas volume density.
Figure 6 shows, for all LPs, the line opacities we derive for the upper-state levels for each line transition from the best-fit, minimum-χ2 2-component model results. We confirm the common assumption that the CO lines are optically thick and the atomic carbon fine-structure lines are optically thin. The CO line opacity depends on both the level population in the upper energy level state (the effective CO column density) and the galaxy-wide turbulent velocity dispersion. For a fixed column density, the higher the turbulent velocity, the lower the line opacity (see, e.g., Narayanan & Krumholz 2014). As shown for both components in each of the LPs, the CO line opacity first increases with Jup before it decreases progressively, as the individual level populations are less frequently excited out to higher J.
Figure 6. Best-fit results from the 2-component model for the calculated line opacities. Left: CO line opacity vs. rotational quantum number, Jup. Right: [C i] line opacity vs. quantum level number. The solid black line indicates an optical depth of unity. The average best-fit, minimum-χ2 model uncertainty is smaller than the marker size.
Download figure:
Standard image High-resolution imageFigure 6 also shows that the CO lines often do not freely radiate their emission, i.e., they are still optically thick, until Jup = 6–8 and Jup = 8–15 in components one and two, respectively. The more highly excited second component remains optically thick beyond Jup = 15 in some cases. Also, as the second component is warmer and denser, the Jup = 0 and Jup = 1 levels are less populated; therefore, more systems may exhibit optically thin CO (1−0) line emission in this more highly excited component. In general, beyond CO (8−7), the contribution to the total CO partition drops significantly and molecules will populate those higher states less frequently on average.
Importantly, the gas does not need to be diffuse in order to be optically thin. In fact, the second component, which we discuss later to be the denser component (Section 6.2.2), has more instances of the CO (1−0) line being optically thin. The lower-density gas has a higher opacity and a CO partition function that is weighed heavily by the lower-J lines. Our results show that as the density increases, the lines become more distributed across the CO partition function, which results in optically thin CO (1−0) line emission in the denser gas. This is consistent with theoretical work of Narayanan & Krumholz (2014), which had utilized both hydrodynamic simulations and radiative transfer analyses in order to calculate the CO line excitation for various idealized disk and merger galaxies at z > 1.
6.2.2. Characterizing the Molecular ISM Properties
Table 5 shows the mean and standard deviation value across the sample of LPs for the main free parameters. Note that the median values for the sample of LPs do not differ within the uncertainties. The LPs have a mean H2 gas density and galaxy-wide mean turbulent velocity of  log(
log( )
) = 4.3 ± 0.9 cm−3 and
= 4.3 ± 0.9 cm−3 and  ΔVturb
ΔVturb  = 125 ± 40 km s−1, respectively. The mean values of the gas kinetic temperatures for both components in the 2-component model are roughly equivalent to the mean kinetic temperature using the Turbulence model—despite the inherent differences in the physical assumptions of each model.
= 125 ± 40 km s−1, respectively. The mean values of the gas kinetic temperatures for both components in the 2-component model are roughly equivalent to the mean kinetic temperature using the Turbulence model—despite the inherent differences in the physical assumptions of each model.
Table 5. Mean Parameter Values for the Sample LPs
log10(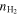 ) ) |
Tk | Td | Tk/Td | κvir | ΔVturb |
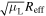
|
GDMR | MISM | [C i]/H2 |
|---|---|---|---|---|---|---|---|---|---|
| (cm−3) | (K) | (K) | (km s−1 pc−1 cm3/2) | (km s−1) | (pc) | (M⊙) | |||
| 4.31 ± 0.88 | 119 ± 77 | 44.7 ± 9.75 | 2.56 ± 1.30 | 1.45 ± 0.36 | 125 ± 40 | 13534 ± 3147 | 130 ± 4.2 | 2.68E+12 ± 1.28E+12 | 6.82E−05 ± 3.04E−05 |
Note. The mean and standard deviation for all χ2-weighted mean parameter values across the sample of LPs, as evaluated for each parameter value from ∼2 million model evaluations.
Download table as: ASCIITypeset image
Using the derived dust temperature, we find the mean ratio of  Tkin/Td
Tkin/Td = 2.6 ± 1.3. For mean densities above ∼104.5 cm−3, the value of Tkin/Td converges closer to unity as the molecular gas and dust become coupled (Goldsmith 2001). This is indeed derived for the denser component, i.e., component two, which has a higher mean density but lower Tkin/Td for the 2-component model. This is also consistent in the Turbulence model results, as the LPs with higher mean density have lower values of Tkin/Td. The mean apparent radius of the LPs is found to be
= 2.6 ± 1.3. For mean densities above ∼104.5 cm−3, the value of Tkin/Td converges closer to unity as the molecular gas and dust become coupled (Goldsmith 2001). This is indeed derived for the denser component, i.e., component two, which has a higher mean density but lower Tkin/Td for the 2-component model. This is also consistent in the Turbulence model results, as the LPs with higher mean density have lower values of Tkin/Td. The mean apparent radius of the LPs is found to be  for the Turbulence model. For the 2-component model, we derive a mean effective radius of
for the Turbulence model. For the 2-component model, we derive a mean effective radius of  and ∼3.3 kpc for the more diffuse and denser components, respectively.
and ∼3.3 kpc for the more diffuse and denser components, respectively.
We explore the relationship between the value of Tkin and H2 gas density in Figure 7. We plot the best-fit, minimum-χ2 solutions obtained for both components in the 2-component model. We also compare to the best-fit, minimum-χ2 model results from the more physically motivated Turbulence model. In general, for the 2-component model, the first component tends to have a lower H2 gas density than the second component. There is a large dispersion in the value of Tkin for both components, although the first component tends to have more values at lower Tkin. Since we find a similar range in Tkin for both components, it is clear that indeed the higher-J CO lines are driven mostly by the fact that the densities are higher and that the Tkin plays a secondary role. This relation between the second component of the 2-component model and the observed high-J CO transitions is shown for all of the LPs in the online supplemental version to this manuscript. As shown, the second component may be largely unconstrained and have best-fit, minimum-χ2 solutions for the density that are unlikely based on examination of the more realistic results for the Turbulence model. Figure 7 also shows that for the best-fit, minimum-χ2 values of the H2 gas density for the 2-component model, the second component is always denser than the first. We find that the dominant emitting component associated with the excitation of the lower-J CO lines has a mean volume density log( ) = 2.2–3.7 cm−3, while the second component has a mean volume density log(
) = 2.2–3.7 cm−3, while the second component has a mean volume density log( ) = 3.2–6.4 cm−3, consistent with the observed trends in the line opacities seen in Figure 6. Altogether, the LPs have a pervasive, dense, and highly active ISM with an average gas kinetic temperature
) = 3.2–6.4 cm−3, consistent with the observed trends in the line opacities seen in Figure 6. Altogether, the LPs have a pervasive, dense, and highly active ISM with an average gas kinetic temperature  Tkin
Tkin = 120 ± 77 K. The median values for both components in the 2-component model are ∼81 and ∼137 K for component one and two, respectively. The Kendall's tau coefficient τ = 0.05 indicates that the gas kinetic temperatures of component one and component two are uncorrelated. This suggests that the diffuse (component one) gas and dense (component two) gas, although both relatively warm, share a distinct range of temperatures. The two-sample Kolmogorov–Smirnov test also confirms that the gas kinetic temperatures likely share a different distribution for components one and two, respectively, with a p-value of 0.06.31
= 120 ± 77 K. The median values for both components in the 2-component model are ∼81 and ∼137 K for component one and two, respectively. The Kendall's tau coefficient τ = 0.05 indicates that the gas kinetic temperatures of component one and component two are uncorrelated. This suggests that the diffuse (component one) gas and dense (component two) gas, although both relatively warm, share a distinct range of temperatures. The two-sample Kolmogorov–Smirnov test also confirms that the gas kinetic temperatures likely share a different distribution for components one and two, respectively, with a p-value of 0.06.31
Figure 7. Best-fit, minimum-χ2 solutions for the H2 gas volume density and gas kinetic temperature derived for the 2-component and Turbulence models (log–log scale). We also show representative errors for both models.
Download figure:
Standard image High-resolution imageTo evaluate the apparent FIR luminosities, we compute the integrated rest-frame FIR (40–120 μm) dust SED. As noted above in Section 5, in the Turbulence model we add together the 50 LVG calculations that sample the mean gas density pdf (constant GDMR for each calculation), to further derive the total dust SED. We calculate a wide range in apparent FIR luminosities among the LPs of  , with the corresponding dust temperatures of ∼40–50 K. The contribution, per component, of the FIR luminosity is approximately divided among the LPs for the 2-component model. The more highly excited component contributes ∼50% of the total μLLFIR, on average, with a large dispersion. Following the traditional method in Kennicutt & Evans (2012), we integrate the total IR luminosity between 8 and 1000 μm to derive a mean apparent μLSFR = (35.6 ± 4.4) × 103
, with the corresponding dust temperatures of ∼40–50 K. The contribution, per component, of the FIR luminosity is approximately divided among the LPs for the 2-component model. The more highly excited component contributes ∼50% of the total μLLFIR, on average, with a large dispersion. Following the traditional method in Kennicutt & Evans (2012), we integrate the total IR luminosity between 8 and 1000 μm to derive a mean apparent μLSFR = (35.6 ± 4.4) × 103  . With an average magnification factor of 20, this would correspond to an intrinsic mean SFR for the LPs of order 1500 M⊙ yr−1.
. With an average magnification factor of 20, this would correspond to an intrinsic mean SFR for the LPs of order 1500 M⊙ yr−1.
The dust opacity for the LPs becomes unity for each component at wavelengths comparable to what is expected, i.e., ≥rest-frame 100 μm. This is consistent with other studies of optically thick dust within the ISM of local and high-z star-forming systems (Blain et al. 2003; Greve et al. 2012; Huang et al. 2014; Hodge et al. 2016; Lutz et al. 2016; Spilker et al. 2016; Simpson et al. 2017). Overall, there is a range of values for λ0, from a few tens of μm to ∼100–300 μm for both component one and component two.32
We find a range of values  (1–10) × 1023 cm−2 and
(1–10) × 1023 cm−2 and  (0.5–50) × 1024cm−2 for component one and component two, respectively. We estimate the effective optical extinction, AV (in magnitudes), using the result for the Milky Way from Güver & Özel (2009), i.e.,
(0.5–50) × 1024cm−2 for component one and component two, respectively. We estimate the effective optical extinction, AV (in magnitudes), using the result for the Milky Way from Güver & Özel (2009), i.e.,
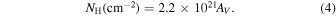
We find a value of AV > 450, for a fiducial value of  1 × 1024 cm−2 for the LPs. The H2 gas column densities in the second component of the most extreme LPs resemble regions similar to local starbursts and even comparable to the rare, highly dust enshrouded local starbursts exceeding
1 × 1024 cm−2 for the LPs. The H2 gas column densities in the second component of the most extreme LPs resemble regions similar to local starbursts and even comparable to the rare, highly dust enshrouded local starbursts exceeding  1024–25 cm−2 (Sanders & Mirabel 1996; Scoville et al. 2017b)). The 2-component model does not recover small regions, and therefore any emission from such compact, high gas column density, galactic nucleus regions would not dominate the total emission. In fact, the Turbulence model indicates that the smallest regions, corresponding to the highest gas density, contribute a negligible amount to the total line and dust SEDs (Figure 4). It is often assumed that for dusty star-forming galaxies, with SFRs > 100–1000 M⊙ yr−1, the thermal dust emission transitions from optically thick to optically thin beyond wavelengths of ∼100 μm or more (Casey et al. 2018a, 2018c). This assumption is also verified in local star-forming systems (e.g., Downes et al. 1993; Scoville et al. 2014, 2016) but is difficult to constrain based on limited observations of individual high-z systems.
1024–25 cm−2 (Sanders & Mirabel 1996; Scoville et al. 2017b)). The 2-component model does not recover small regions, and therefore any emission from such compact, high gas column density, galactic nucleus regions would not dominate the total emission. In fact, the Turbulence model indicates that the smallest regions, corresponding to the highest gas density, contribute a negligible amount to the total line and dust SEDs (Figure 4). It is often assumed that for dusty star-forming galaxies, with SFRs > 100–1000 M⊙ yr−1, the thermal dust emission transitions from optically thick to optically thin beyond wavelengths of ∼100 μm or more (Casey et al. 2018a, 2018c). This assumption is also verified in local star-forming systems (e.g., Downes et al. 1993; Scoville et al. 2014, 2016) but is difficult to constrain based on limited observations of individual high-z systems.
6.2.3. Total Molecular ISM Mass Estimates
We define the total, apparent, molecular gas mass,33
 , based on our non-LTE radiative transfer LVG calculations of the H2 gas column density and the effective radius. The H2 gas column density is directly proportional to the volume density,
, based on our non-LTE radiative transfer LVG calculations of the H2 gas column density and the effective radius. The H2 gas column density is directly proportional to the volume density,  , multiplied by the equivalent path length of the molecules, i.e.,
, multiplied by the equivalent path length of the molecules, i.e.,  , and therefore yields, together with the effective radius,
, and therefore yields, together with the effective radius,

The velocity gradient, δv/δr, is averaged across the modeled molecular gas component, which is assumed to fill the source solid angle. This corresponds to the mass of each component, i.e., the total mass for the 2-component model is the sum of both components. The Turbulence model density pdf is sampled by 50 density bins, each of which has an associated solid angle and allows for 50 individual mass calculations. The total μLMISM is the sum of all of the masses corresponding to the full density pdf. We use the value of μLMISM derived in the Turbulence model to estimate a range for the mean total molecular ISM mass of μLMISM = 3.6 × 1011–1.6 × 1013 M⊙. The 2-component model-derived μLMISM is broadly consistent with the Turbulence model, although the latter tends to be larger by up to a factor of ∼1.5. The inherent power-law dependence between density and gas kinetic temperature of the Turbulence model prevents overdense solutions for the mean density in the lognormal pdf and thus drives a realistic turnover in the CO line intensity at higher J. Therefore, in the Turbulence model there is more diffuse gas, on average, which contributes a larger fraction to the total molecular ISM mass. In contrast, the 2-component model tends to fit the higher-J lines with a stronger contribution from the second, denser component, which contributes less to the total mass.
The mass of the more highly excited component in the 2-component model (i.e., component two) can be thought of as a tracer of dense molecular gas (Gowardhan et al. 2017). The best-fit, minimum-χ2 model solutions in our sample of LPs indicate a median and mean value of MISM,c2/MISM,total = 25% and 30%, respectively, for this proxy for the dense molecular gas fraction believed to be more closely associated with current SF. Therefore, the more diffuse/less excited component carries most of the mass. The larger mass fraction for component one is due to the larger size of that component, which scales nonlinearly with the mass (Equation (5)).
The LPs have an average apparent total molecular gas mass μLMISM = 2.5 × 1012 M⊙. If this would be transformed into stars, this theoretical gas depletion time, τdep, results in a timescale on the order of τdep =  μLMISM
μLMISM /
/ μLSFR
μLSFR = (2.5 × 1012)/(35.4 × 103) ∼ 70 Myr. This rapid depletion timescale is an order of magnitude lower than the 1 Gyr gas depletion time observed in local star-forming galaxies (Leroy et al. 2013; Saintonge et al. 2013, 2016), in agreement with the strong redshift dependence summarized by Tacconi et al. (2018, 2020). This further supports the notion that these systems lie above the main sequence for star-forming galaxies at z ∼ 2–3 (Whitaker et al. 2012). We use the derived values for
= (2.5 × 1012)/(35.4 × 103) ∼ 70 Myr. This rapid depletion timescale is an order of magnitude lower than the 1 Gyr gas depletion time observed in local star-forming galaxies (Leroy et al. 2013; Saintonge et al. 2013, 2016), in agreement with the strong redshift dependence summarized by Tacconi et al. (2018, 2020). This further supports the notion that these systems lie above the main sequence for star-forming galaxies at z ∼ 2–3 (Whitaker et al. 2012). We use the derived values for  to also calculate the surface gas mass density
to also calculate the surface gas mass density  800–22,000 M⊙ pc−2. Note that the magnification factors cancel to first order. The total mean values of some of the LPs may be largely unconstrained, due to the lack of ancillary [C i] data, the lack of strong dust photometric support (other than Planck data alone), or an insufficient amount of CO line detections. These LPs sample the higher end of the observed molecular gas mass surface densities when compared to local star-forming galaxies (Schmidt 1959; Downes & Solomon 1998; Kennicutt & Evans 2012; Bolatto et al. 2013; see also Section 7.2.2). The active star-forming regions of the LPs are, however, extended by 25–100× larger in area, with an intrinsic emitting size radius of order a few kiloparsecs (∼3 kpc; see Section 7.2.1).
800–22,000 M⊙ pc−2. Note that the magnification factors cancel to first order. The total mean values of some of the LPs may be largely unconstrained, due to the lack of ancillary [C i] data, the lack of strong dust photometric support (other than Planck data alone), or an insufficient amount of CO line detections. These LPs sample the higher end of the observed molecular gas mass surface densities when compared to local star-forming galaxies (Schmidt 1959; Downes & Solomon 1998; Kennicutt & Evans 2012; Bolatto et al. 2013; see also Section 7.2.2). The active star-forming regions of the LPs are, however, extended by 25–100× larger in area, with an intrinsic emitting size radius of order a few kiloparsecs (∼3 kpc; see Section 7.2.1).
6.3. Atomic Carbon Gas Excitation
In total, 21/24 LPs have one or both of the [C i] emission lines detected. Only 5/24 LPs have a single carbon line detection, while the remaining 16/24 LPs have measurements of both fine-structure lines. The [C i] measurements of the LPs represent the brightest apparent [C i] line fluxes reported at high z (Brown & Vanden Bout 1992; Barvainis et al. 1997; Weiß et al. 2003, 2005a; Walter et al. 2011; Alaghband-Zadeh et al. 2013; Bothwell et al. 2017; Yang et al. 2017; Andreani et al. 2018). Strong turbulent mixing of the cool neutral media in the ISM may likely occur in these turbulent LPs (Xie et al. 1995), allowing for enriched [C i]/H2 abundances in the interiors of molecular clouds and thus strong [C i] emission. Both theoretical and observational studies have demonstrated the reliability of using [C i] to trace the overall kinematics of the cold gas, as well as to determine the total molecular gas mass (Papadopoulos & Greve 2004; Papadopoulos et al. 2004; Weiß et al. 2005a; Glover & Clark 2014; Tomassetti et al. 2014; Glover et al. 2015; Israel et al. 2015; Israel 2020). The latter requires knowledge of the atomic carbon excitation temperature, Texc, and gas-phase abundance, [C i]/H2, to accurately convert the [C i] line emission to the atomic carbon mass, MC, and further to the total molecular gas mass MISM (Weiß et al. 2003, 2005a).
We first examine which density phase the [C i] line emission predominantly arises from. The left-hand side of Figure 8 plots the relative integrated flux values for the [C i] (1−0) and [C i] (2−1) lines from component one, with respect to the total integrated flux value for both components combined, for the 2-component model. We remove from the figure the five LPs with only a single [C i] line to avoid misinterpreting our results. Almost all of the [C i] (1−0) and [C i] (2−1) line emission in the LPs comes from the first component. In general, the first component is best traced by the [C i] (1−0) line. In general, this indicates that the carbon lines can be reliable tracers of the bulk gas mass, since we have shown in Section 6.2.3 that the first component in the 2-component model carries most of the total mass. One of the LPs, LPsJ1139, seems to have a significant contribution from the denser component as indicated by the low contribution to the overall [C i] line emission from component one. This is due to its unusually high [C i] (2−1) to [C i] (1−0) line ratio (Nesvadba et al. 2019), although the CO (7−6) line reported by Cañameras et al. (2018b) appears to consistently underpredict the model-derived line flux density. The right-hand side of Figure 8 further reveals the relationship between the [C i] (1−0) velocity-integrated line fluxes and H2 density based on the Turbulence model. As suggested by the more simplistic 2-component model, the Turbulence model shows that the diffuse gas, with log( ) = 2–3 cm−3, is primarily responsible for the [C i] (1−0) line emission. For such active star-forming systems, this implies that the carbon lines are well suited to predominantly trace the diffuse molecular gas.
) = 2–3 cm−3, is primarily responsible for the [C i] (1−0) line emission. For such active star-forming systems, this implies that the carbon lines are well suited to predominantly trace the diffuse molecular gas.
Figure 8. Left: relative [C i] (1−0) and [C i] (2−1) line flux densities for component 1 vs. the combined line flux densities for both components in the 2-component model. The red square indicates that both [C i] lines predominantly arise from the denser component, i.e., component 2. Right: for each of the LPs we plot (log–log scale) the relative contribution to the total [C i] (1−0) line flux derived in the Turbulence model, from the 50 individual [C i] (1−0) line fluxes corresponding to the 50 H2 densities that sample the density pdf.
Download figure:
Standard image High-resolution imageNext, we investigate the atomic carbon Texc for this diffuse molecular gas phase traced by the [C i] lines. In particular, our non-LTE analysis enables us to test the validity of the optically thin, LTE assumption framework that is commonly applied to detections of [C i] lines in star-forming galaxies. The measurement of both ground-state [C i] lines can, in principle, provide an independent estimate to constrain the carbon Texc (Stutzki et al. 1997; Schneider et al. 2003). The use of the carbon line ratio, ![${R}_{[{\rm{C}}{\rm\small{I}}]}$](https://content.cld.iop.org/journals/0004-637X/908/1/95/revision1/apjabcc01ieqn91.gif) =
= }^{{\prime} }/{L}_{[{\rm{C}}\,{\rm\small{I}}](1\mbox{--}0)}^{{\prime} }$](https://content.cld.iop.org/journals/0004-637X/908/1/95/revision1/apjabcc01ieqn92.gif) , to determine Texc requires two major assumptions: (i) that the line emission is optically thin, and (ii) that the lines are excited under LTE conditions, as defined in the Boltzmann equation:
, to determine Texc requires two major assumptions: (i) that the line emission is optically thin, and (ii) that the lines are excited under LTE conditions, as defined in the Boltzmann equation: ![${T}_{\mathrm{exc},\mathrm{LTE}}\,=38.8/\mathrm{ln}(2.11/R([{\rm{C}}\,{\rm\small{I}}]))$](https://content.cld.iop.org/journals/0004-637X/908/1/95/revision1/apjabcc01ieqn93.gif) K (Stutzki et al. 1997; Schneider et al. 2003). The value of Texc can differ for each of the line transitions, i.e., the temperature needed to recover the relative populations of the upper/lower levels from a Boltzmann distribution.
K (Stutzki et al. 1997; Schneider et al. 2003). The value of Texc can differ for each of the line transitions, i.e., the temperature needed to recover the relative populations of the upper/lower levels from a Boltzmann distribution.
We briefly return to Figure 6, based on our best-fit, minimum-χ2 2-component models, to recall that the majority of the LPs have optically thin [C i] (1−0) and [C i] (2−1) lines. This also supports the capability of using the optically thin [C i] lines as a strong tracer of the bulk atomic carbon column density. We further calculate the value of the flux-weighted [C i] (1−0) excitation temperature, Texc([C i] (1−0)), using the relative integrated flux values from both components of the 2-component model. In addition, we also calculate the equivalent flux-weighted [C i] (1−0) line Texc using the individual gas properties corresponding to the 50 density bins used to sample the density pdf derived in the Turbulence model.
We find the average luminosity-weighted excitation temperature of Texc([C i] (1−0)) ∼ 40 K for the 2-component model and Texc([C i] (1−0)) ∼ 32 K for the Turbulence model. Note the mean value of Texc([C i] (2−1)) ∼ 29 K for the Turbulence model. In the LTE assumption, Texc  Texc[C i] (1−0) = Texc[C i] (2−1). The LPs have a systematically lower value of Texc[C i] (2−1) than Texc[C i] (1−0), up to 25%–30% in some cases, reflecting those subthermal gas excitation conditions. Figure 9 compares our derived, flux-weighted value of Texc[C i] (1−0) using both models to the optically thin, LTE assumed value for the Texc, as presented in Stutzki et al. (1997) and Schneider et al. (2003). In general, our model-derived values agree with the ideal framework of assuming that the atomic carbon excitation occurs within optically thin, LTE gas conditions, yet we find that some of the LPs would have had systematically underpredicted values of the carbon Texc under these ideal assumptions. This emphasizes the importance in non-LTE modeling to better understand the subthermal excitation of the cold atomic and molecular ISM in star-forming galaxies. Our results for Texc can also be compared with the recent large compilation of all local and high-z star-forming systems with [C i] detections (Valentino et al. 2020b). They assume the same LTE assumptions as in Schneider et al. (2003), yielding Texc of ∼25 K with a moderate dispersion. This includes the high-z starburst/quasar sample of Walter et al. (2011), which had an average excitation of ∼30 K when using the same optically thin, LTE assumptions.
Texc[C i] (1−0) = Texc[C i] (2−1). The LPs have a systematically lower value of Texc[C i] (2−1) than Texc[C i] (1−0), up to 25%–30% in some cases, reflecting those subthermal gas excitation conditions. Figure 9 compares our derived, flux-weighted value of Texc[C i] (1−0) using both models to the optically thin, LTE assumed value for the Texc, as presented in Stutzki et al. (1997) and Schneider et al. (2003). In general, our model-derived values agree with the ideal framework of assuming that the atomic carbon excitation occurs within optically thin, LTE gas conditions, yet we find that some of the LPs would have had systematically underpredicted values of the carbon Texc under these ideal assumptions. This emphasizes the importance in non-LTE modeling to better understand the subthermal excitation of the cold atomic and molecular ISM in star-forming galaxies. Our results for Texc can also be compared with the recent large compilation of all local and high-z star-forming systems with [C i] detections (Valentino et al. 2020b). They assume the same LTE assumptions as in Schneider et al. (2003), yielding Texc of ∼25 K with a moderate dispersion. This includes the high-z starburst/quasar sample of Walter et al. (2011), which had an average excitation of ∼30 K when using the same optically thin, LTE assumptions.
Figure 9. Luminosity-weighted excitation temperature of the atomic carbon [C i] (1−0) line based on both the 2-component model (red circle) and Turbulence model (maroon diamond) is shown on the x-axis. These values are compared to the predicted value based on the assumption of optically thin, LTE gas conditions (Schneider et al. 2003).
Download figure:
Standard image High-resolution imageThere are 5/16 LPs with both [C i] detections for which the Turbulence model still predicts low-excitation temperatures of the [C i] (1−0) line of ≤20 K. These are therefore overpredicted according to the simplified LTE assumption. We note that the low values of Texc in these LPs are accompanied by their relatively low line ratios between the [C i] (2−1) and [C i] (1−0). At values of Texc ≤ 20 K, Weiß et al. (2005a) demonstrated that the atomic carbon mass estimate will increase exponentially. Many of the LPs show substantially subthermal gas excitation, as shown from the Texc[C i] (1−0) values. This may be due to the enhanced molecular gas kinetic temperatures with respect to the carbon excitation temperature, Tkin/Texc[C i] (1−0) ∼ 4. Therefore, blind LTE assumptions would have strongly impacted the inferred total carbon mass and relative abundance in those galaxies by about an order of magnitude. If the [C i] lines are completely dominated by subthermal gas excitation, the model-derived value of Texc will be higher by up to a factor of 2–3 in the 2-component model. There is considerably less scatter in the Turbulence model, which is likely due to the differences in these models when deriving the carbon gas-phase abundance.
We recall that we have restricted the CO/H2 abundance to a Milky Way value of ∼10−4, close to that of local star-forming systems with CO/H2 = (0.5–1) × 10−4. We do, however, allow the value of [C i]/H2 to vary as a free parameter in both models. We find, for the Turbulence model, the sample mean for the LPs of  [C i]/H2
[C i]/H2 = (6.82 ± 3.04) × 10−5. To better understand the 2-component model, we note that if the value of [C i]/H2 were increased in the second component to match that of the first component, then the [C i] emission would always be close to LTE (since the H2 density of component two is always higher than the first component (Figure 7). The 2-component model solves this by reducing the value of [C i]/H2 in the second component, so that the emission is dominated by the subthermally excited emission from the first component. Thus, the value of [C i]/H2 in the second component must be lower; otherwise, the models would result in higher than observed line ratios. This is one of the main criteria for the Turbulence modeling procedure, which realistically forces the gas-phase carbon abundance to decrease with increasing H2 densities according to a power-law relation.
= (6.82 ± 3.04) × 10−5. To better understand the 2-component model, we note that if the value of [C i]/H2 were increased in the second component to match that of the first component, then the [C i] emission would always be close to LTE (since the H2 density of component two is always higher than the first component (Figure 7). The 2-component model solves this by reducing the value of [C i]/H2 in the second component, so that the emission is dominated by the subthermally excited emission from the first component. Thus, the value of [C i]/H2 in the second component must be lower; otherwise, the models would result in higher than observed line ratios. This is one of the main criteria for the Turbulence modeling procedure, which realistically forces the gas-phase carbon abundance to decrease with increasing H2 densities according to a power-law relation.
At high z, knowledge of the excitation conditions and abundance of carbon is often the main source of uncertainty. The mean value of [C i]/H2 we find for the LPs is comparable to previous estimates by local/high-z studies, although typically this has been achieved via the inferred H2 mass from single (low-J) CO transitions (Weiß et al. 2005a; Walter et al. 2011; Valentino et al. 2020b). We caution that there is an order-of-magnitude dispersion in [C i]/H2 among the LPs, which has strong implications for the inferred conversion from the [C i] line luminosity to MISM in star-forming galaxies (as discussed in Section 7.2.2). Some high-z carbon gas-phase abundance estimates are a few × 10−5 (Walter et al. 2011), which are broadly consistent with those of low-z galaxies. This suggests that the starbursts and QSOs have at least solar gas-phase metallicities or higher (Gerin & Phillips 2000; Weiß et al. 2001; Israel & Baas 2002, 2003). Overall, we find values often lower than the abundance derived in the solar neighborhood of [C i]/H2 ∼ 3.5 × 10−4 (Anders & Grevesse 1989). In some cases, the LPs show similar [C i]/H2 abundances to the cold Milky Way CO-faint clouds, with ∼(1–2) × 10−5 (Frerking et al. 1989; Keene et al. 1997).
7. Discussion
7.1. Molecular Gas Excitation at High z
7.1.1. Classifying the Gas Physical Conditions in the LPs
Figure 5 shows that the LPs offer a rich perspective into the wide range of gas excitation properties of CO for high-z star-forming galaxies. Overall, there seems to be a continuous distribution in gas excitation conditions for this sample of LPs. The high magnification therefore allows us to probe an intrinsically heterogeneous mix of dusty star-forming galaxies. Following the classification scheme defined by Rosenberg et al. (2015) for the diverse sample of local IR-luminous star-forming galaxies, we apply the parameter, hereafter "xclass," to quantify the range of excitation conditions in these 24 LPs. This parameter specifically characterizes the drop-off slope, after the expected peak of the CO line SED of Jup = 5–7. For each individual galaxy, we compare the relative line luminosity strength (in L⊙) of the higher-J CO (Jup = 11–13) lines versus the mid-J CO (Jup = 5–7) lines:

with three excitation classes defined as xclass1 = [<0.33], xclass2 = [0.33, 0.66], and xclass3 = [>0.66]. The sample of LPs indeed shows a broad range of excitation conditions based on these three different CO line SED classifications, with a continuum of xclass values. In total, there are 14 LPs within xclass1, five LPs within xclass2, and five LPs within xclass3. We note that the three z ∼ 1 LPs are all in xclass1; however, the distribution of z and classification is well mixed for the z = 2–3.5 subsample. Figure 10 shows the classification versus the FIR luminosity, indicating a clear relation between these two quantities, despite the strong incompleteness in our flux-limited sample of LPs, based on their selection criteria. The correlation we observe between xclass, or more broadly the CO line ratios, and the FIR luminosity is consistent with previous studies of star-forming galaxies (Greve et al. 2014; Rosenberg et al. 2015).
Figure 10. Plot (log–log scale) between xclass and FIR luminosity, based on the best-fit, minimum-χ2 Turbulence models. For details on the classification scheme, see Section 7.1.2 and Equation (6).
Download figure:
Standard image High-resolution image7.1.2. Mean CO Brightness Temperature Ratios at z > 1
The CO line luminosities,  , normalized to the CO (1−0) line, are often used to study the global gas excitation conditions of a galaxy and the line SEDs (e.g., Bothwell et al. 2013). Here we use our data set of the LPs, based on approximately four to six CO lines for each of the LPs, to better understand the CO line SEDs of such IR-bright, z > 1 galaxies. These
, normalized to the CO (1−0) line, are often used to study the global gas excitation conditions of a galaxy and the line SEDs (e.g., Bothwell et al. 2013). Here we use our data set of the LPs, based on approximately four to six CO lines for each of the LPs, to better understand the CO line SEDs of such IR-bright, z > 1 galaxies. These  ratios are also used to scale the higher-J CO lines to the ground-state transition to infer the total molecular gas mass (Carilli & Walter 2013). The sample mean and standard deviation for the LPs are reported in Table 4. The LPs have line brightness temperature ratios that are often well below unity (i.e., subthermal line excitation).
ratios are also used to scale the higher-J CO lines to the ground-state transition to infer the total molecular gas mass (Carilli & Walter 2013). The sample mean and standard deviation for the LPs are reported in Table 4. The LPs have line brightness temperature ratios that are often well below unity (i.e., subthermal line excitation).
In Figure 11 we use the Turbulence model to show all of the best-fit CO line luminosities,  , normalized to the CO (1−0) line. We also show the stacked brightness temperature ratios of the lensed SPT sample (Spilker et al. 2016) and the stacked values of the unlensed, z ∼ 2.5 main-sequence star-forming galaxies (Boogaard et al. 2020; Riechers et al. 2020). The former tends to represent the higher gas excitation seen in a subset of the LPs. The latter, which considers only seven sources in the stacked value, tends to agree with both the model-derived average values for R3,1, R7,1, and R8,1. The LPs also show significantly higher line ratios than the z ∼ 1–2, main-sequence star-forming galaxies in the COSMOS field, for the available values of R4,1 = 0.27, R5,1 = 0.21, and R7,1 = 0.06 (Valentino et al. 2020a).34
Galaxies on the brightest end of the QSO luminosity function, at z ∼ 2–4, tend to have R5,1 ∼ 1 (e.g., Weiß et al 2007; Bischetti et al. 2021), which suggests that there may be a differing dominant gas excitation mechanism for the global ISM of the LPs that have a mean value of R5,1 ∼ 0.37.
, normalized to the CO (1−0) line. We also show the stacked brightness temperature ratios of the lensed SPT sample (Spilker et al. 2016) and the stacked values of the unlensed, z ∼ 2.5 main-sequence star-forming galaxies (Boogaard et al. 2020; Riechers et al. 2020). The former tends to represent the higher gas excitation seen in a subset of the LPs. The latter, which considers only seven sources in the stacked value, tends to agree with both the model-derived average values for R3,1, R7,1, and R8,1. The LPs also show significantly higher line ratios than the z ∼ 1–2, main-sequence star-forming galaxies in the COSMOS field, for the available values of R4,1 = 0.27, R5,1 = 0.21, and R7,1 = 0.06 (Valentino et al. 2020a).34
Galaxies on the brightest end of the QSO luminosity function, at z ∼ 2–4, tend to have R5,1 ∼ 1 (e.g., Weiß et al 2007; Bischetti et al. 2021), which suggests that there may be a differing dominant gas excitation mechanism for the global ISM of the LPs that have a mean value of R5,1 ∼ 0.37.
Figure 11. Turbulence model results for the best-fit, minimum-χ2 model solutions for the CO line luminosities,  , normalized to the CO (1−0) line, for the LPs. The average line ratios derived using the Turbulence model (maroon diamonds) are compared to the values from the LPs and K19 sample (red star), which are purely based on observations, with median line ratio values determined by normalizing each line by a common FIR luminosity. In addition, we plot representative local IR-bright star-forming galaxies from Rosenberg et al. (2015), with increasing classifications determined by their excitation conditions, from lowest to highest: Class I (light-blue solid line), Class II (orange solid line), and Class III (magenta solid line). Yellow pentagons represent stacked values for the lensed SPT galaxies (Spilker et al. 2016), compared to the stacked value of z ∼ 2.5 main-sequence star-forming galaxies (green squares) from the ASPECS sample (Walter et al. 2016; Boogaard et al. 2020; Riechers et al. 2020).
, normalized to the CO (1−0) line, for the LPs. The average line ratios derived using the Turbulence model (maroon diamonds) are compared to the values from the LPs and K19 sample (red star), which are purely based on observations, with median line ratio values determined by normalizing each line by a common FIR luminosity. In addition, we plot representative local IR-bright star-forming galaxies from Rosenberg et al. (2015), with increasing classifications determined by their excitation conditions, from lowest to highest: Class I (light-blue solid line), Class II (orange solid line), and Class III (magenta solid line). Yellow pentagons represent stacked values for the lensed SPT galaxies (Spilker et al. 2016), compared to the stacked value of z ∼ 2.5 main-sequence star-forming galaxies (green squares) from the ASPECS sample (Walter et al. 2016; Boogaard et al. 2020; Riechers et al. 2020).
Download figure:
Standard image High-resolution imageThe local IR-bright star-forming galaxies from Rosenberg et al. (2015) are also shown in Figure 11, according to their increasing classifications determined by their gas excitation conditions, from lowest to highest: Class I, Class II, and Class. For reference the Milky Way has a global average value of R3,1 of 0.28 ± 0.17 (Fixsen et al. 1999). The LPs show a broad range of gas excitation, although most have higher line ratios than both Class II and Class III galaxies, which are representative of most local (U)LIRGs (see also Papadopoulos et al. 2012b; Lu et al. 2014; Kamenetzky et al. 2016). The LPs show systematically higher excitation than most local IR-bright, spiral galaxies, as well as the more highly excited local radio/X-ray AGN host galaxies (van der Werf et al. 2010; Papadopoulos et al. 2012b; Spinoglio et al. 2012; Meijerink et al. 2013; Liu et al. 2015; Rosenberg et al. 2015; Kamenetzky et al. 2016). Papadopoulos et al. (2011) report values of R3,1 =0.67 and R6,1 = 0.2–1.6 for local (U)LIRGs (Papadopoulos et al. 2012a). This is, overall, consistent with earlier studies and the value we obtain for the LPs. Local star-forming systems with 9 < log(LIR) < 12 show a median value of R3,1 to be close to 0.5 (Mauersberger et al. 1999), with some 60 local barred galaxies and starbursts having an average value of R3,1 close to 0.9 ± 0.1 (Yao et al. 2003). Overall, the line brightness temperature ratios for the LPs are usually not as high as one of the most IR-luminous local starburst galaxies, M82 (Weiß et al. 2005b), which has a global average R2,1, R3,1, R4,1, and R5,1 of 0.98, 0.93, 0.85, and 0.75, respectively. Bothwell et al. (2013) previously interpreted the mean CO line SED of 32 z > 1 star-forming galaxies, by normalizing their CO line luminosities by a common FIR luminosity, while others normalized to a common measurement of the dust continuum at 1.4 mm (Spilker et al. 2016). Based on our simultaneous modeling of the lines and continuum, we can test whether or not this is a valid method for building a mean line SED shape. It has been well known that the FIR luminosity and CO line luminosity tend to increase with one another proportionally (Greve et al. 2012; Liu et al. 2015; Valentino et al. 2020a), and Figure 10 also shows that the CO excitation is correlated with the FIR luminosity. Hence, there is still a bias when using the FIR luminosity to compute a mean CO line SED. Although the line ratios are sensitive to the FIR luminosity, different subsets of high-z sources do not have every line detected. There are also different selection biases; therefore, a common FIR luminosity may be used to normalize each line detection in an attempt to remove these biases and to avoid physically misleading line ratios when comparing large samples.
To do this, we use the LPs and K19 z ∼ 1–7 sample (hereafter "LPs and K19 sample"; Ngal = 269). To construct this compilation, we used our data set for the LPs including the database compiled in Kirkpatrick et al. (2019), which includes a vast majority of the heterogeneously selected samples of high-z galaxies with CO line detections (including Carilli & Walter 2013; Pope et al. 2013; Aravena et al. 2014; Sharon et al. 2016; Yang et al. 2017; Frayer et al. 2018; Perna et al. 2018; Kirkpatrick et al. 2019). Following previous studies, each CO line is normalized by a common FIR luminosity (LFIR = 1 × 1012.5 L⊙). The values listed in Table 4 are derived using the LPs and K19 z ∼ 1–7 CO line compilation, which consists of 90 CO (1−0), 86 CO (2−1), 128 CO (3−2), 80 CO (4−3), 68 CO (5−4), 73 CO (6−5), 63 CO (7−6), 39 CO (8−7), 33 CO (9−8), 14 CO (10−9), 15 CO (11−10), and 2 CO (12−11) high-z line measurements.
As shown in both Table 4 and Figure 11, the average results from our best-fit, minimum-χ2 Turbulence models are strikingly similar to the median brightness temperature ratios derived from the FIR luminosity-normalized lines we calculate from the CO line observations alone using the LPs and K19 sample, or the "All Sources" sample of Kirkpatrick et al. (2019), which considers all z > 1 galaxies with CO line detections. In Table 4 we also reference the average line ratios, up to the R5,1 ratio, from Carilli & Walter (2013), which is based on the available data for (sub)millimeter bright, star-forming galaxies (SMGs) and QSOs at the time. We also quote in Table 4 the comparable and the more recent values reported by Kirkpatrick et al. (2019). We note that the values from the latter are consistent with the low- to mid-J CO line ratios reported by other recent studies of lensed SMGs at z > 1 (Yang et al. 2017; Cañameras et al. 2018b).
At first glance, our results would seem to support this method of using the FIR luminosity to normalize the CO lines to derive a mean CO line SED; however, the sparse amount of well-sampled CO line SEDs per galaxy in the literature suggests that the dispersions of three or more orders of magnitude in the observed line intensities (Figure 2) all average out. The LPs and K19 z ∼ 1–7 sample includes some of the brightest (sub)millimeter-selected galaxies with multiple CO line detections, which further exaggerates the effects of averaging large samples of z > 1 galaxies (Bothwell et al. 2013; Spilker et al. 2016; Yang et al. 2017; Cañameras et al. 2018b). As noted by Narayanan & Krumholz (2014), there can be a factor of 5–10 difference in the CO line SEDs, at mid- to high-J transitions, for similarly selected, (sub)millimeter-bright galaxies with the same integrated FIR luminosity. The broad range of excitation conditions and average line ratios we present for the LPs further highlights the notion that it is unlikely for there to be a template CO line SED for any z > 1 galaxy population. As noted throughout this work, our results agree with the theoretical models of Narayanan & Krumholz (2014) for the CO line SEDs of z > 1 star-forming galaxies, as parameterized by the SFR surface density. This suggests that in the absence of multiple CO line measurements, an SFR surface density estimate may be combined with limited line data and further use the theoretical models of Narayanan & Krumholz (2014) to estimate the CO line SED.
7.2. Molecular Gas Mass Estimates
7.2.1. Intrinsic Emitting Size Regions
One way to constrain whether or not the LPs are not only some of the most massive, gas-rich star-forming galaxies but also perhaps the largest in size is to cross-examine the model-derived radius with the intrinsic source size—as expected from studies of star-forming galaxies at z > 1. As presented in Section 6.2.2, the mean value we derive from the Turbulence model for the radius of the modeled source-emitting region is  . The intrinsic source size may differ. When comparing to other observed sources, we assume that the observed emission corresponds to a filled, face-on circular disk (see, e.g., Weiß et al 2007) with an effective radius. This sets a lower limit to the true source size, as there is no information of how the gas and dust emission is distributed within the source solid angle. We recall again the lens magnification factor estimates for the LPs in Table 1, as they will be used to estimate the intrinsic emitting size. For a reference, we derive an average value of μL for the LPs using the upper limit value of μL in Table 1. For galaxies without a published value of μL, we use the value based on the "Tully–Fisher" argument presented in Harris et al. (2012) and our CO (1−0) line measurements (see Appendix A). The average lens magnification factor has a value of μL ∼ 20. The expected, intrinsic, total line- and continuum-emitting size radius for all of the LPs
. The intrinsic source size may differ. When comparing to other observed sources, we assume that the observed emission corresponds to a filled, face-on circular disk (see, e.g., Weiß et al 2007) with an effective radius. This sets a lower limit to the true source size, as there is no information of how the gas and dust emission is distributed within the source solid angle. We recall again the lens magnification factor estimates for the LPs in Table 1, as they will be used to estimate the intrinsic emitting size. For a reference, we derive an average value of μL for the LPs using the upper limit value of μL in Table 1. For galaxies without a published value of μL, we use the value based on the "Tully–Fisher" argument presented in Harris et al. (2012) and our CO (1−0) line measurements (see Appendix A). The average lens magnification factor has a value of μL ∼ 20. The expected, intrinsic, total line- and continuum-emitting size radius for all of the LPs  . This size is consistent overall with the size of the dust continuum emission from massive star-forming galaxies at z = 1–3 (1–5 kpc; Simpson et al. 2015; Barro et al. 2016; Hodge et al. 2016; Oteo et al. 2016, 2017; Rujopakarn et al. 2016; Fujimoto et al. 2017; Jiménez-Andrade et al. 2019; Hodge & da Cunha 2020).
. This size is consistent overall with the size of the dust continuum emission from massive star-forming galaxies at z = 1–3 (1–5 kpc; Simpson et al. 2015; Barro et al. 2016; Hodge et al. 2016; Oteo et al. 2016, 2017; Rujopakarn et al. 2016; Fujimoto et al. 2017; Jiménez-Andrade et al. 2019; Hodge & da Cunha 2020).
We can further test the reliability of our Turbulence model if we consider two of the LPs with estimates of the intrinsic, lens model reconstruction of the source size, based on high angular resolution data: LPsJ105353 (Cañameras et al. 2017a) and LPsJ0209 (Geach et al. 2018; Rivera et al. 2019). As summarized in Harrington et al. (2019) for LPsJ0209,35
the lens model reconstruction from the low-J CO line image presented in both Geach et al. (2018) and Rivera et al. (2019) suggests a molecular gas reservoir with an emitting radius of ∼1–2 kpc. The flux-weighted mean magnification factor derived for this source is ∼15, corresponding to an expected intrinsic emitting radius for LPsJ0209 of  . Note that we are modeling the full extent of the CO (1−0) to CO (15–14) line emission. Therefore, our modeling is consistent with the independently derived source-plane radius derived from both the CO (4−3) and CO (3−2) emission lines within the overall uncertainties. Based on CO (1−0) line observations of high-z galaxies, the factor of two difference can be accounted for, as the easily excited CO (1−0) line emission is expected to be more extended on average (Emonts et al. 2014; Casey et al. 2018b; Spingola et al. 2020). LPsJ10535336
is proposed to consist of two independent regions (roughly 1.5 kpc in length along the major axis) in the reconstructed source-plane CO (4−3) line image (Cañameras et al. 2017a), each separated by ∼500 pc, corresponding to an intrinsic emitting size radius of ∼2 kpc. Our modeling would suggest an expected intrinsic emitting radius for LPsJ105353 of
. Note that we are modeling the full extent of the CO (1−0) to CO (15–14) line emission. Therefore, our modeling is consistent with the independently derived source-plane radius derived from both the CO (4−3) and CO (3−2) emission lines within the overall uncertainties. Based on CO (1−0) line observations of high-z galaxies, the factor of two difference can be accounted for, as the easily excited CO (1−0) line emission is expected to be more extended on average (Emonts et al. 2014; Casey et al. 2018b; Spingola et al. 2020). LPsJ10535336
is proposed to consist of two independent regions (roughly 1.5 kpc in length along the major axis) in the reconstructed source-plane CO (4−3) line image (Cañameras et al. 2017a), each separated by ∼500 pc, corresponding to an intrinsic emitting size radius of ∼2 kpc. Our modeling would suggest an expected intrinsic emitting radius for LPsJ105353 of  , which is consistent within the uncertainties considering both the lens model and our radiative transfer model. Thus, the intrinsic size may play a role in understanding the high apparent fluxes. A magnification factor of 50 would be required to reduce the mean value we derive from the Turbulence model, i.e.,
, which is consistent within the uncertainties considering both the lens model and our radiative transfer model. Thus, the intrinsic size may play a role in understanding the high apparent fluxes. A magnification factor of 50 would be required to reduce the mean value we derive from the Turbulence model, i.e.,  , to match the more common size expected for z > 1 star-forming galaxies of ∼2 kpc. Since the average magnification factor for the LPs is ∼20, the size of these systems may be one of the primary physical parameters responsible for explaining their extreme IR luminosity.
, to match the more common size expected for z > 1 star-forming galaxies of ∼2 kpc. Since the average magnification factor for the LPs is ∼20, the size of these systems may be one of the primary physical parameters responsible for explaining their extreme IR luminosity.
7.2.2. Converting  and
and ![${L}_{[{\rm{C}}\,{\rm\small{I}}]}^{{\prime} }$](data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAAEAAAABCAQAAAC1HAwCAAAAC0lEQVR42mNkYAAAAAYAAjCB0C8AAAAASUVORK5CYII=) to MISM
to MISM
We use the results of the more realistic Turbulence model (Section 6) to calculate the derived values of both αCO and ![${\alpha }_{[{\rm{C}}{\rm\small{I}}]}$](https://content.cld.iop.org/journals/0004-637X/908/1/95/revision1/apjabcc01ieqn108.gif) (hereafter without units attached to ease readability; M⊙ (K km s−1 pc2)−1) conversion factors between the line luminosity and total molecular gas mass, MISM. We refer to these factors with respect to the ground-state transitions, CO (1−0) and [C i] (1−0), unless otherwise noted. Figure 12 shows the results for the value of αCO based on a representative set of low- to high-J CO transitions, versus the minimum-χ2 model solution for the total molecular gas mass, for all of the LPs. The CO (1−0) and CO (3−2) derived αCO values are less scattered than those derived from CO (9−8) and CO (11−10) transitions. This demonstrates that the lower-J lines are more reliable tracers of MISM, as expected.
(hereafter without units attached to ease readability; M⊙ (K km s−1 pc2)−1) conversion factors between the line luminosity and total molecular gas mass, MISM. We refer to these factors with respect to the ground-state transitions, CO (1−0) and [C i] (1−0), unless otherwise noted. Figure 12 shows the results for the value of αCO based on a representative set of low- to high-J CO transitions, versus the minimum-χ2 model solution for the total molecular gas mass, for all of the LPs. The CO (1−0) and CO (3−2) derived αCO values are less scattered than those derived from CO (9−8) and CO (11−10) transitions. This demonstrates that the lower-J lines are more reliable tracers of MISM, as expected.
Figure 12. CO line to molecular gas mass conversion factor, αCO, value vs. μMISM for the CO (1−0) (gold diamond), CO (4−3) (orange diamond), CO (7−6) (thin red diamond), CO (9−8) (gray circle), and CO (11−10) (black cross) lines, as derived from the best-fit, minimum-χ2 Turbulence models (log–log scale).
Download figure:
Standard image High-resolution imageTo consider the use of [C i] line emission as a tracer of MISM, we recall the results in Section 6.3, in particular, (i) the [C i] lines are optically thin, and (ii) most of the carbon emission arises from the more diffuse line-emitting region (i.e., component one from the 2-component model) with log( ) ∼ 2–3 cm−3—which is the cold gas component responsible for the bulk of the total MISM (also see Figure 8). The value of
) ∼ 2–3 cm−3—which is the cold gas component responsible for the bulk of the total MISM (also see Figure 8). The value of }$](https://content.cld.iop.org/journals/0004-637X/908/1/95/revision1/apjabcc01ieqn110.gif) can be used to convert the optically thin
can be used to convert the optically thin }^{{\prime} }$](https://content.cld.iop.org/journals/0004-637X/908/1/95/revision1/apjabcc01ieqn111.gif) measurement to MISM, for which we find an average value of
measurement to MISM, for which we find an average value of  for the LPs with both [C i] lines detected. Crocker et al. (2019) recently studied a sample of 22 local spiral galaxies, representing a wide range of SFR and stellar masses, using spatially resolved Herschel SPIRE observations of CO and [C i]. They found a lower value of
for the LPs with both [C i] lines detected. Crocker et al. (2019) recently studied a sample of 22 local spiral galaxies, representing a wide range of SFR and stellar masses, using spatially resolved Herschel SPIRE observations of CO and [C i]. They found a lower value of }=7.9$](https://content.cld.iop.org/journals/0004-637X/908/1/95/revision1/apjabcc01ieqn113.gif) , with a factor of 1.5–2 uncertainty. There are differences in these values of
, with a factor of 1.5–2 uncertainty. There are differences in these values of }$](https://content.cld.iop.org/journals/0004-637X/908/1/95/revision1/apjabcc01ieqn114.gif) for the LPs, as compared to these less extreme local star-forming galaxies, yet this may be due to differences in the calibration. Our current work performs a full radiative transfer analysis, while Crocker et al. (2019) had used an intensity–intensity correlation between the low-J CO and [C i] line emission and an assumed value of αCO. The latter was determined previously by Sandstrom et al. (2013) based on an assumed range in the GDMR and assumed line ratios. Another recent study used an alternative method to first measure [C i] and H2 absorption lines from gamma-ray burst and QSO objects (Heintz & Watson 2020). Thereafter they determine the value of
for the LPs, as compared to these less extreme local star-forming galaxies, yet this may be due to differences in the calibration. Our current work performs a full radiative transfer analysis, while Crocker et al. (2019) had used an intensity–intensity correlation between the low-J CO and [C i] line emission and an assumed value of αCO. The latter was determined previously by Sandstrom et al. (2013) based on an assumed range in the GDMR and assumed line ratios. Another recent study used an alternative method to first measure [C i] and H2 absorption lines from gamma-ray burst and QSO objects (Heintz & Watson 2020). Thereafter they determine the value of }\sim 21$](https://content.cld.iop.org/journals/0004-637X/908/1/95/revision1/apjabcc01ieqn115.gif) for an assumed solar metallicity, which is consistent with our derived values.
for an assumed solar metallicity, which is consistent with our derived values.
Based on the Turbulence model, we find an average value for the LPs of  , with a factor of 10 dispersion and a mean value of
, with a factor of 10 dispersion and a mean value of  for the galaxies with the best dust photometry and CO/[C i] line coverage. Note that the scatter in the conversion factors comes from the scatter in the line luminosities and total molecular gas masses used to derive the mass-to-light conversion for each of the LPs. Therefore, a single conversion factor value would not reflect this intrinsic dispersion among the sample.
for the galaxies with the best dust photometry and CO/[C i] line coverage. Note that the scatter in the conversion factors comes from the scatter in the line luminosities and total molecular gas masses used to derive the mass-to-light conversion for each of the LPs. Therefore, a single conversion factor value would not reflect this intrinsic dispersion among the sample.
Almost all of the LPs have a value of αCO that is higher than the local IR (ultra)luminous star-forming galaxy (aka "ULIRG") conversion factor of αCO = 0.8 (Downes & Solomon 1998). The ULIRG value was derived using similar LVG approximations using only the available low-J CO lines, as well as dynamical mass measurements of the concentrated nuclear starburst regions. The warm, diffuse, and dense molecular gas that pervades the molecular medium of local IR-luminous star-forming galaxies was not fully traced by the CO (1−0) and CO (2−1) lines (Downes & Solomon 1998). The lower-J lines only trace the diffuse and warm gas under these active star-forming conditions, and therefore they correspond to lower values of αCO. We have also shown this in our best-fit, minimum-χ2 model CO line SEDs, where the CO (1−0) line emission arises mostly from the diffuse molecular gas with density log( ) ∼2 cm−3, while the gas at these lower densities has higher kinetic temperatures. A lower value of αCO would be inferred for the LPs if limited to only the low-J CO lines tracing this warm and diffuse phase, and thereby neglecting the higher-density gas that is required to excite the higher-J CO lines. Therefore, our physical results are still consistent with the general conclusions in modeling the local ULIRGs (Downes & Solomon 1998), yet we have modeled the substantial contributions to the overall CO line SED from warm and dense gas of the order of Tkin ∼ 120 K and log(
) ∼2 cm−3, while the gas at these lower densities has higher kinetic temperatures. A lower value of αCO would be inferred for the LPs if limited to only the low-J CO lines tracing this warm and diffuse phase, and thereby neglecting the higher-density gas that is required to excite the higher-J CO lines. Therefore, our physical results are still consistent with the general conclusions in modeling the local ULIRGs (Downes & Solomon 1998), yet we have modeled the substantial contributions to the overall CO line SED from warm and dense gas of the order of Tkin ∼ 120 K and log( ) = 4–5 cm−3. This explains why our overall result reflects higher values of αCO ∼ 3.4 for the LPs.
) = 4–5 cm−3. This explains why our overall result reflects higher values of αCO ∼ 3.4 for the LPs.
Figure 13 shows our derived conversion factors as a function of both the mean H2 gas density and gas kinetic temperature. Almost half of the 24 LPs have low values of αCO = 1–2 and are associated with higher gas kinetic temperatures (Tkin > 120 K). The left-hand side of Figure 13 shows a nonlinear decrease in αCO as a function of increasing Tkin, whereas the right-hand side of Figure 13 suggests a strong rise in αCO for increasing H2 gas density. The LPsJ0209, a known radio AGN/starburst, has one of the highest values, as well as the highest-redshift source in our sample, LPsJ105322 (z ∼ 3.5). They both have well-sampled dust SEDs and CO line [C i] lines, yet we still derive the highest values of  , albeit with larger uncertainty. In future work we will investigate the statistical relationship between αCO and these parameters. Since the LPsJ0209 source is known to have a compact radio AGN (Geach et al. 2015), future studies may explore the reasons whether or not star-forming galaxies with coeval AGN activity (Harrington et al. 2019) may tend to show higher values of αCO. In fact, the AGN APM0827 has a relatively high value of αCO ∼ 5 and log(
, albeit with larger uncertainty. In future work we will investigate the statistical relationship between αCO and these parameters. Since the LPsJ0209 source is known to have a compact radio AGN (Geach et al. 2015), future studies may explore the reasons whether or not star-forming galaxies with coeval AGN activity (Harrington et al. 2019) may tend to show higher values of αCO. In fact, the AGN APM0827 has a relatively high value of αCO ∼ 5 and log( ) ∼ 5 cm−3 (Weiß et al 2007).
) ∼ 5 cm−3 (Weiß et al 2007).
Figure 13. Turbulence model-derived αCO factor vs. H2 gas density (log-x scale). The color bar denotes the gas kinetic temperature. These are the total χ2-weighted parameter mean and standard deviation values derived from the ∼2 million model calculations. The canonical ULIRG and Milky Way values for αCO are αCO = 0.8 and 4.3 M⊙ (K km s−1 pc2)−1, respectively.
Download figure:
Standard image High-resolution imageThe large range observed for the LPs suggests a strong diversity in gas excitation properties among this relatively small sample. It seems incorrect to assume a common value for high-z star-forming galaxies, as discussed previously in the context of a continuity of gas excitation conditions and the corresponding variation in the conversion factor (e.g., Casey et al. 2014). The two different values commonly applied have been based on a simplified bimodal population of star-forming galaxies (e.g., Daddi et al. 2010), yet more complex two-population models are successfully reproducing several observed properties in observed high-z galaxies (Sargent et al. 2014). The latter may be tested with assumptions of a continuity in gas excitation conditions for different galaxy populations. Variations of the overall CO gas-phase abundance and variations across a turbulent star-forming disk will alter the conversion factor (Wolfire et al. 2010; Glover & Mac Low 2011; Shetty et al. 2011a, 2011b; Narayanan et al. 2012; Bolatto et al. 2013; Narayanan & Krumholz 2014); therefore, it is possible for a wide variation in αCO to exist for a given gas column density.
In Figure 14, we examine the relation between the derived αCO and ![${\alpha }_{[{\rm{C}}{\rm\small{I}}]}$](https://content.cld.iop.org/journals/0004-637X/908/1/95/revision1/apjabcc01ieqn122.gif) conversion factors with the gas mass surface density in the sample of LPs. The rather extreme galaxy-integrated surface gas mass densities for the LPs are accompanied by a wide range in the conversion factor we derive. Previous works (Tacconi et al. 2008) have suggested that as the gas mass surface density goes beyond 100 M⊙ pc−2, i.e., comparable to GMCs in the Milky Way and nearby galaxies, the value of αCO decreases. Figure 14 indicates that our analyses suggest the possibility of a factor of 10 dispersion of αCO in the range of
conversion factors with the gas mass surface density in the sample of LPs. The rather extreme galaxy-integrated surface gas mass densities for the LPs are accompanied by a wide range in the conversion factor we derive. Previous works (Tacconi et al. 2008) have suggested that as the gas mass surface density goes beyond 100 M⊙ pc−2, i.e., comparable to GMCs in the Milky Way and nearby galaxies, the value of αCO decreases. Figure 14 indicates that our analyses suggest the possibility of a factor of 10 dispersion of αCO in the range of  M⊙ pc−2, yet a positive trend. Since the C i emission is optically thin, the conversion factor must increase. This drives the value we derive for
M⊙ pc−2, yet a positive trend. Since the C i emission is optically thin, the conversion factor must increase. This drives the value we derive for ![${\alpha }_{[{\rm{C}}{\rm\small{I}}]}$](https://content.cld.iop.org/journals/0004-637X/908/1/95/revision1/apjabcc01ieqn124.gif) to higher values, which are comparable to the value of αCO for those low-metallicity nearby galaxies. The average value of αCO is slightly lower than the Galactic value (Bolatto et al. 2013). Overall, the sample mean value for the LPs is similar to the value of αCO = 3.6 derived using clumpy disk dynamical mass model calculations for near-IR-selected galaxies at z ∼ 1.5 (Daddi et al. 2010). In general, lower Tkin and both higher
to higher values, which are comparable to the value of αCO for those low-metallicity nearby galaxies. The average value of αCO is slightly lower than the Galactic value (Bolatto et al. 2013). Overall, the sample mean value for the LPs is similar to the value of αCO = 3.6 derived using clumpy disk dynamical mass model calculations for near-IR-selected galaxies at z ∼ 1.5 (Daddi et al. 2010). In general, lower Tkin and both higher  and log(
and log( ) seem to increase the value of αCO based on our full radiative transfer modeling of the LPs. Comparable spatially resolved data sets would allow for such robust tests of functional forms between these parameters to enable a thorough comparison among this sample of LPs. For example, Maloney & Black (1988) considered
) seem to increase the value of αCO based on our full radiative transfer modeling of the LPs. Comparable spatially resolved data sets would allow for such robust tests of functional forms between these parameters to enable a thorough comparison among this sample of LPs. For example, Maloney & Black (1988) considered  (Scoville et al. 2012), while others have proposed a weaker dependence on the gas kinetic temperature, i.e.,
(Scoville et al. 2012), while others have proposed a weaker dependence on the gas kinetic temperature, i.e.,  (Dickman 1985; Shetty et al. 2011a).
(Dickman 1985; Shetty et al. 2011a).
Figure 14. Turbulence model-derived CO and [C i] line to molecular ISM mass conversion factors, plotted against the molecular ISM gas mass surface density, with αCO and ![${\alpha }_{[{\rm{C}}{\rm\small{I}}]}$](https://content.cld.iop.org/journals/0004-637X/908/1/95/revision1/apjabcc01ieqn129.gif) denoted as circles and crosses, respectively (log–log scale). The color bar denotes the gas kinetic temperature, Tkin. Also shown are the values for αCO derived in the Milky Way and the local IR-luminous star-forming systems (see Bolatto et al. 2013). Both plots report the total χ2-weighted parameter mean and standard deviation values derived from the ∼2 million model calculations.
denoted as circles and crosses, respectively (log–log scale). The color bar denotes the gas kinetic temperature, Tkin. Also shown are the values for αCO derived in the Milky Way and the local IR-luminous star-forming systems (see Bolatto et al. 2013). Both plots report the total χ2-weighted parameter mean and standard deviation values derived from the ∼2 million model calculations.
Download figure:
Standard image High-resolution image7.2.3. Comparisons between MISM Estimates Derived from Optically Thin, Dust Continuum Methods
The simultaneous modeling of the CO, [C i], and dust continuum emission enables a robust comparison to the inferred value of total molecular ISM mass, MISM, based only on the properties of the dust SED. Recently, there has been a growing set of methods using dust continuum measurements to infer the MISM in star-forming galaxies, although observations of dust and its effects have been used to derive gas column densities over many years. Previous studies have integrated information about the visual extinction, gas-to-dust mass ratio, CO line luminosity to MISM conversion factor, αCO, and observations of the thermal dust continuum along the assumed optically thin, Rayleigh–Jeans side of the emission spectrum (Lilley 1955; Heiles 1967; Savage & Code 1970; Aannestad & Purcell 1973; Emerson et al. 1973; Hildebrand et al. 1977; Hildebrand 1983; Young et al. 1986; Lonsdale & Hacking 1987; Solomon & Sage 1988; Scoville et al. 1991, 2014, 2016, 2017a; Young & Scoville 1991; Blain & Longair 1993; Kruegel & Siebenmorgen 1994; Young et al. 1996; Solomon et al. 1997; Calzetti et al. 2000; Genzel et al. 2010; Leroy et al. 2011; Magdis et al. 2012; Magnelli et al. 2012; Förster Schreiber et al. 2018; Tacconi et al. 2018; Coogan et al. 2019; Kaasinen et al. 2019).
The use of a single-band dust continuum measurement to estimate MISM is based on the assumption that the rest-frame dust continuum emission is optically thin beyond λrest ≥ 250 μm (recently highlighted by Scoville et al. 2014, 2016, 2017a). The method of Scoville et al. (2014, 2016, 2017a) (hereafter the "1 mm method") uses the inferred rest-frame 850 μm continuum emission and derives an empirical calibration of the dust opacity per unit ISM mass. The estimate is increasing for the total MISM based on larger samples with CO (1−0) line measurements, enabling further calibrations of this method (e.g., Kaasinen et al. 2019). In the 1 mm method, a Milky Way value of αCO = 6.5 (Scoville et al. 1987, 2017a) is applied for the absolute scaling from CO (1−0) line luminosity to the total MISM. The 1 mm method uses a cold and so-called "mass-weighted" dust temperature, Td = 25 K (Scoville et al. 2014; Liang et al. 2018, 2019), rather than the so-called "luminosity-weighted" value determined from template or modified blackbody SED fit results. Although these values are not inherently weighted by the luminosity, Scoville et al. (2014, 2016, 2017a) advocate that such template/graybody fitting will be driven by the warmest and brightest dust components. In addition, Scoville et al. (2014, 2016, 2017a) assume that most of the dust mass is in the colder phases and will therefore be unaccounted for if the total molecular gas mass is derived using the results for the dust temperature based on a template/graybody SED fit. So far, this assumption has not been demonstrated explicitly using combined non-LTE radiative transfer modeling of the line and continuum SEDs. Here we explore whether or not the bulk dust mass likely arises from dust with colder temperatures. In fact, we suspect that both the warm and diffuse dust will contribute both to the total dust mass and the SED. Both of the best-fit models (see, e.g., Figure 4) suggest that the dust SED is dominated by warm and relatively diffuse gas with densities between log( ) ∼ 2 and 4 cm−3, which correspond to the densities contributing most of the molecular ISM mass (see Section 6.2.3). In the following, we test the hypothesis of the 1 mm method, which assumes that the global values of the mass-weighted and luminosity-weighted dust temperatures are different, using our model results. Since our models provide the dust temperature, mass, and luminosity for each gas component, we can compute mass- and luminosity-weighted dust temperatures for each galaxy as
) ∼ 2 and 4 cm−3, which correspond to the densities contributing most of the molecular ISM mass (see Section 6.2.3). In the following, we test the hypothesis of the 1 mm method, which assumes that the global values of the mass-weighted and luminosity-weighted dust temperatures are different, using our model results. Since our models provide the dust temperature, mass, and luminosity for each gas component, we can compute mass- and luminosity-weighted dust temperatures for each galaxy as
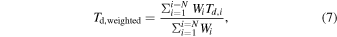
where  is the mass-weighted or luminosity-weighted value, N = 2 for the 2-component model and N = 50 for the Turbulence model, since we have 50 individual calculations of the dust temperature and mass. A similar approach in deriving a mass-weighted value of the dust temperature is reported by Förster Schreiber et al. (2018), although they implemented a dust mass weight based on the value from an assembly of templates. The results of our calculations are shown in Figure 15, using the rest-frame L850 μm value to calculate our luminosity-weighted dust temperature. Here we use the rest-frame L850 μm (see, e.g., Spilker et al. 2016); however, our following conclusions remain valid if we use rest-frame L500 μm. We note that our definition of luminosity-weighted dust temperature is not the same as that referred to in Scoville et al. (2014, 2016, 2017a), as the mean value from template/graybody fitting is considered the luminosity-weighted average. The dust temperatures from our models, before any weighting, are consistent, within 1σ uncertainties, with previously determined values of the dust temperatures from modified blackbody fits (Cañameras et al. 2015; Harrington et al. 2016). Overall, the values we derive for the LPs span a range common to high-z dusty star-forming galaxies. Therefore, the high apparent IR luminosity for the LPs does not bias our results to sources with higher dust temperatures.
is the mass-weighted or luminosity-weighted value, N = 2 for the 2-component model and N = 50 for the Turbulence model, since we have 50 individual calculations of the dust temperature and mass. A similar approach in deriving a mass-weighted value of the dust temperature is reported by Förster Schreiber et al. (2018), although they implemented a dust mass weight based on the value from an assembly of templates. The results of our calculations are shown in Figure 15, using the rest-frame L850 μm value to calculate our luminosity-weighted dust temperature. Here we use the rest-frame L850 μm (see, e.g., Spilker et al. 2016); however, our following conclusions remain valid if we use rest-frame L500 μm. We note that our definition of luminosity-weighted dust temperature is not the same as that referred to in Scoville et al. (2014, 2016, 2017a), as the mean value from template/graybody fitting is considered the luminosity-weighted average. The dust temperatures from our models, before any weighting, are consistent, within 1σ uncertainties, with previously determined values of the dust temperatures from modified blackbody fits (Cañameras et al. 2015; Harrington et al. 2016). Overall, the values we derive for the LPs span a range common to high-z dusty star-forming galaxies. Therefore, the high apparent IR luminosity for the LPs does not bias our results to sources with higher dust temperatures.
Figure 15. L850 μm, weighted dust temperature, Td, vs. the mass-weighted value of Td for both the 2-component model and the Turbulence model. The calculations are described in Section 7.2.3.
Download figure:
Standard image High-resolution imageTwo immediate outcomes from this exercise are as follows: (1) the mass-weighted Td value and luminosity-weighted Td value for both models are remarkably consistent with one another, with a one-to-one correlation observed for all of the LPs when using the more realistic Turbulence model; and (2) the mass-weighted Td value for both models is consistently higher than the advocated value of Td = 25 K in the 1 mm method for star-forming galaxies. The mass-weighted value was justified by Scoville et al. (2014) to reflect the fact that the dust grains exposed to strong radiative heating would represent a so-called luminosity-weighted dust temperature. We demonstrate, using two separate models, that it is instead justified to use the effective luminosity-weighted dust temperature, e.g., as derived in a dust SED fit, when using the 1 mm method to calculate MISM. We find a one-to-one correlation among the mass-weighted and luminosity-weighted Td values, indicating that the dust mass in the LPs primarily consists of relatively warm diffuse gas, in contrast to the assumed cold diffuse dust content in the Milky Way. We stress, however, that the often-used optically thin MBB fit should not be used since it underestimates Td compared to models with a realistic transition wavelength between the optically thin and optically thick emission regimes of the dust (Jin et al. 2019; Cortzen et al. 2020).
We further demonstrate the effects this may have in Figure 16, which shows the value of μLMISM derived using three separate methods. The first two methods are our full radiative transfer calculations of μLMISM, as computed using the 2-component model and the Turbulence model. We compute the final estimate of μLMISM for the LPs, using the 1 mm method and the respective AzTEC or ALMA ∼1 mm dust continuum measurements (Harrington et al. 2016; D. Berman et al. 2021, in preparation), a mass-weighted Td = 25 K, and a value of  (which is consistent with our modeling procedure; Section 5). Overall, the 1 mm method systematically overpredicts μLMISM, consistent with other work (Förster Schreiber et al. 2018; Liu et al. 2019). This confirms that the assumed mass-weighted Td in the 1 mm method are too low to explain the LPs, as the value we use for the GDMR in our modeling is comparable to that used in the empirical calibration presented most recently in Scoville et al. (2017a). In some cases, the discrepancy may be larger than a factor of two, and this is likely due to the large dispersion we find for the LPs for the average value of αCO. In a recent study by Kaasinen et al. (2019), the rest-frame 850 μm luminosity was also used to cross-calibrate the mass estimate. They found a factor of two discrepancy in the total molecular gas mass estimates using both spatially resolved CO (1−0) line emission, with an assumed αCO = 6.5 M⊙ (K km s−1 pc2)−1, and a spatially resolved dust continuum measurement used to infer the rest-frame 850 μm emission and the 1 mm method described above (assuming the same value of
(which is consistent with our modeling procedure; Section 5). Overall, the 1 mm method systematically overpredicts μLMISM, consistent with other work (Förster Schreiber et al. 2018; Liu et al. 2019). This confirms that the assumed mass-weighted Td in the 1 mm method are too low to explain the LPs, as the value we use for the GDMR in our modeling is comparable to that used in the empirical calibration presented most recently in Scoville et al. (2017a). In some cases, the discrepancy may be larger than a factor of two, and this is likely due to the large dispersion we find for the LPs for the average value of αCO. In a recent study by Kaasinen et al. (2019), the rest-frame 850 μm luminosity was also used to cross-calibrate the mass estimate. They found a factor of two discrepancy in the total molecular gas mass estimates using both spatially resolved CO (1−0) line emission, with an assumed αCO = 6.5 M⊙ (K km s−1 pc2)−1, and a spatially resolved dust continuum measurement used to infer the rest-frame 850 μm emission and the 1 mm method described above (assuming the same value of  as we have used).
as we have used).
Figure 16. Mass–mass plot (log–log scale) of apparent total molecular gas mass, μLMISM, derived using three methods. The y-axis shows the result using a single continuum measurement of the thermal dust emission and an assumed mass-weighted Td = 25 K based on the scaling methods described in Scoville et al. (2017a). The x-axis indicates the values of μLMISM, as derived for both the 2-component model and the Turbulence model.
Download figure:
Standard image High-resolution imageFor many of the LPs, the value of αCO is less than the standard value used in the 1 mm method. For global comparisons between galaxy populations, a single value was deemed appropriate; however, the estimate of MISM for high-z star-forming galaxies may be over- or underestimated on average if the value of αCO is undetermined. The molecular gas and dust are, presumably, well mixed in such turbulent star-forming systems (Krumholz et al. 2018). Since they are believed to trace one another, the single-band ∼1 mm, dust continuum method to derive the MISM has a clear advantage because it is more feasible to obtain a (sub)millimeter continuum detection of a high-z galaxy than it is to detect multiple CO lines and perform a non-LTE radiative transfer analysis to explicitly derive an estimate of MISM. The strong dependencies on the assumed dust SED and gas excitation conditions are important to consider when estimating MISM and therefore motivate further benchmarking between the various methods to derive MISM in high z.
7.3. Heating, Cooling, and Turbulence-regulated SF
SF occurs deep within molecular clouds, and this process requires cooling to aid gravitational collapse. At relatively high gas column densities, the kinetic energy transferred to CO molecules is converted to line photons, which then radiate that energy away. Therefore, we expect that CO line cooling is the dominant cooling process of the molecular gas-rich star-forming regions within the LPs. At lower column densities the FIR fine-structure lines of singly ionized carbon, [C ii], and neutral and doubly ionized oxygen, [OI] and [OIII], are often considered as the dominant coolants of the star-forming ISM (Hollenbach 1985; Rosenberg et al. 2015; Díaz-Santos et al. 2016). The highly ionized and/or high-temperature (and high-density) regions traced by these FIR fine-structure emission lines are not expected to contribute to the cooling of the gas- and dust-rich molecular gas traced by the CO line measurements of the LPs. The contribution of collisionally excited [C ii] line cooling arises from neutral gas within dense PDRs, corresponding to log( ) ∼ 3 cm−3 and T = 100 K (Hollenbach & Tielens 1997; Goldsmith et al. 2012). Within the denser molecular gas phase we model in this work, we expect that collisional excitations between molecules are believed to play a stronger role as a gas heating term, as opposed to far-UV (FUV) heating from photodissociation regions (PDRs) that lie between the H ii regions and the cold molecular gas (Tielens & Hollenbach 1985). In addition, Meijerink et al. (2011) demonstrate in a pure PDR model that the CO cooling fraction is 3%–5%, while Rosenberg et al. (2015) noticed similar cooling power from the CO lines up to tens of percent of the total cooling budget.37
They observed a strong CO cooling fraction, which does not show a deficit as observed in the FIR fine-structure lines.
) ∼ 3 cm−3 and T = 100 K (Hollenbach & Tielens 1997; Goldsmith et al. 2012). Within the denser molecular gas phase we model in this work, we expect that collisional excitations between molecules are believed to play a stronger role as a gas heating term, as opposed to far-UV (FUV) heating from photodissociation regions (PDRs) that lie between the H ii regions and the cold molecular gas (Tielens & Hollenbach 1985). In addition, Meijerink et al. (2011) demonstrate in a pure PDR model that the CO cooling fraction is 3%–5%, while Rosenberg et al. (2015) noticed similar cooling power from the CO lines up to tens of percent of the total cooling budget.37
They observed a strong CO cooling fraction, which does not show a deficit as observed in the FIR fine-structure lines.
To explore the nature, and possible source(s), of the energy for the total CO line cooling in the LPs, we first calculate the sum  for each CO line luminosity using the best-fit, minimum-χ2 values from the Turbulence model (see Table 8) and derive a range of values for the apparent CO cooling power for the LPs between Σ(
for each CO line luminosity using the best-fit, minimum-χ2 values from the Turbulence model (see Table 8) and derive a range of values for the apparent CO cooling power for the LPs between Σ( ) ∼ 7 × 1042 and ∼5 × 1044 erg s−1. Our analyses of the Turbulence model results suggest that the global molecular ISM in the LPs often has an H2 gas density log(
) ∼ 7 × 1042 and ∼5 × 1044 erg s−1. Our analyses of the Turbulence model results suggest that the global molecular ISM in the LPs often has an H2 gas density log( ) > 4 cm−3 and gas kinetic temperatures between 60 and 150 K. This implies that our estimate is specifically connected to the total cooling budget of this dense molecular gas phase. If we consider this cooling power to be continuous over the mean molecular gas depletion time, of the order of 70 Myr, the total energy emitted is of the order of
) > 4 cm−3 and gas kinetic temperatures between 60 and 150 K. This implies that our estimate is specifically connected to the total cooling budget of this dense molecular gas phase. If we consider this cooling power to be continuous over the mean molecular gas depletion time, of the order of 70 Myr, the total energy emitted is of the order of  erg.
erg.
We can also estimate the turbulent kinetic energy of the molecular gas using the mean intrinsic molecular gas mass we derived in Section 6.2.3 and the mean turbulent velocity dispersion, resulting in  erg. We recall our results for the Turbulence model, with the sample mean galaxy-wide, turbulent velocity dispersions for the LPs of
erg. We recall our results for the Turbulence model, with the sample mean galaxy-wide, turbulent velocity dispersions for the LPs of  km s−1, consistent with the second-moment velocity dispersion maps of line images for high-z star-forming systems (Talia et al. 2018; Leung et al. 2019; Venemans et al. 2019; Yang et al. 2019; Jiménez-Andrade et al. 2020; Neri et al. 2020; Tadaki et al. 2020). Therefore, over the 70 Myr, a considerable amount of energy is responsible for sustaining the continuous CO line emission.
km s−1, consistent with the second-moment velocity dispersion maps of line images for high-z star-forming systems (Talia et al. 2018; Leung et al. 2019; Venemans et al. 2019; Yang et al. 2019; Jiménez-Andrade et al. 2020; Neri et al. 2020; Tadaki et al. 2020). Therefore, over the 70 Myr, a considerable amount of energy is responsible for sustaining the continuous CO line emission.
As noted in Rosenberg et al. (2014), local IR-luminous systems may have various sources of turbulent energy, e.g., merger activity, AGNs, and powerful outflows. Studies predict the coexistence of starburst and AGN activity, particularly at z ∼ 2 (Hopkins et al. 2008), yet the LPs have been shown to be strongly powered by SF rather than an AGN (e.g., Harrington et al. 2016). Nonetheless, we can estimate the relative contribution of mechanical feedback energy from AGN outflow activity. As a reference, one of the most powerful radio-loud QSOs, 3C 82, has a jet power of the order of 1047 erg s−1 (Punsly et al. 2020). Theoretical studies that aim to reproduce the formation of local massive elliptical galaxies have indicated an AGN mechanical outflow energy estimate of the order of 1042–43 erg, with a rate of ∼3 × 10−5 Myr−1 (Gaspari et al. 2012). If we use this AGN episodic rate from Gaspari et al. (2012) and the jet power of 3C 82, we estimate a total power of the order of 1058 erg in 70 Myr—i.e., ≤10% of the total energy radiated away by CO line emission. Note that it is unlikely that all of the mechanical jet power is continuous, nor is it directly transferred into the molecular gas of the ISM, since 3C 82 has a "biconical outflow orientation," with a half opening angle that may not impact the majority of the host galaxy. The mechanical power from AGN jets may also impart a significant amount of energy in the form of galactic outflows, of the order of 1044–46 erg s−1 (Veilleux et al. 2009, 2020; Sharma & Nath 2012; McNamara et al. 2014; Russell et al. 2016). The unconstrained nature of galactic outflows at high z is still to be determined, as the mean gas densities may exceed the jet densities by four or five orders of magnitude (McNamara et al. 2016), and therefore is a caveat in this interpretation.
AGNs may also produce a significant amount of X-ray heating (Meijerink et al. 2006, 2007). X-ray absorption effects in the rest-frame 2–30 keV energy range are pronounced at higher energies. The gas column densities we derive in Section 6.2.2 suggest that we are often in the Compton-thick regime beyond NH > 1024 cm−2 (Hickox & Alexander 2018). Currently, there is no constraint on the X-ray luminosity in the LPs, and we are aware of only one example of a radio AGN, i.e., LPsJ0209 (Geach et al. 2015; Harrington et al. 2019). We also cannot rule out the possibility of a heavily dust-obscured AGN, yet our sample of LPs have a strong selection function biased away from identifying strong QSOs (Yun et al. 2008; Harrington et al. 2016). Although there are limited X-ray studies of dusty star-forming galaxies at z > 1, we are able to estimate a possible energy from an assumed apparent X-ray luminosity, as derived from the apparent SFR for the LPs and a local ratio of  (Mineo et al. 2014). We use an assumed intrinsic spectral shape for a non-AGN X-ray contribution, with an X-ray absorbing gas column density of NH ∼ 1022 cm−2, and infer an apparent X-ray luminosity of the order of 1043 erg s−1. This energy is consistent with other, z ∼ 2–3, FIR-detected X-ray AGN galaxies (Mullaney et al. 2011, 2012).
(Mineo et al. 2014). We use an assumed intrinsic spectral shape for a non-AGN X-ray contribution, with an X-ray absorbing gas column density of NH ∼ 1022 cm−2, and infer an apparent X-ray luminosity of the order of 1043 erg s−1. This energy is consistent with other, z ∼ 2–3, FIR-detected X-ray AGN galaxies (Mullaney et al. 2011, 2012).
Since we expect much of the intervening gas column densities to be up to three orders of magnitude higher than this assumed value, this likely reflects an extreme upper limit. This corresponds to an apparent X-ray energy of the order of 1059 erg. Although this is equivalent to the CO line cooling, when integrated across the fiducial 70 Myr timescale, it is a strong assumption for the X-ray luminosity to be continuous. Since this may be a strong upper limit, we can also conclude that X-ray luminosity from a non-AGN component is unlikely to be the primary heating mechanism to excite the gas-rich molecular ISM in the LPs.
Cosmic rays, unless inhomegenously distributed, are unlikely to regulate star-forming gas at physical scales larger than 100 pc—although the distribution and random diffusion of cosmic rays are highly uncertain (Thompson et al. 2006; Zweibel 2013). Cosmic-ray heating (see the review by Krumholz 2014) is primarily one of the strongest gas heating mechanisms within cloud interiors when the dust temperatures are ∼20 K and the gas densities are ∼100–1000 cm−3. Beyond gas densities of 104 cm−3, the effects of dust grain–molecular gas energy exchange (via the IR radiation field and/or grain-molecule collisions) are predicted to become stronger, if not dominant over cosmic-ray and FUV heating (Goldsmith 2001; Krumholz et al. 2011; Narayanan & Krumholz 2014). It appears that cosmic-ray heating may not be pervasive throughout the ISM of the LPs, since their mean densities are above 104 cm−3. Both observational and theoretical work suggests that the more diffuse gas, which can extend out to ∼10 kpc, may be strongly influenced by cosmic rays in dusty star-forming galaxies at z ∼ 2–3 (Papadopoulos & Greve 2004; Acciari et al. 2009; Abdo et al. 2010; Bisbas et al. 2015; Falgarone et al. 2017; Indriolo et al. 2018). The relative role of cosmic rays in driving the heating in high-z star-forming galaxies is currently unconstrained, which remains a caveat in this analysis. There is evidence to suggest that the UV radiation field strength determines the relative cosmic-ray ionization rate, and for such galaxies it may be likely that the majority of the cosmic rays are confined to the local star-forming regions within the ISM because the UV radiation decreases faster than the inverse square of the distance from the ionizing source (Indriolo et al. 2018).
Our results for the sample mean value of Tkin/Td = 2–3, on average, suggest galaxy-wide, turbulence-driven, mechanical heating as a signpost for the significantly high SF activity in these high-z galaxies. The Tkin/Td ratio parameter, to zeroth order, may be an interesting parameter to better understand the relative level of mechanical (traced by Tkin) versus photoelectric heating (traced by Td). The local starburst galaxy, NGC 6240, has a large CO line-to-continuum ratio driven by galaxy-wide shocks (i.e., mechanical energy input; Papadopoulos et al. 2014). This scenario seems to be consistent with the large total line widths (Section 4) and highly turbulent star-forming medium inferred for the LPs. Therefore, some form of kinetic activity must be responsible to drive this ratio to higher values, which implies that some form of kinetic energy density must be sustained to distribute the significant molecular gas content within the ISM of the LPs. The values of Tkin/Td = 2–3 are also found in the Milky Way regions with strong interstellar radiation field strengths, G0 = 105, such as the Orion PDR regions (a peak density of log( )∼ 5 cm−3). These regions have a typical visual extinction AV < 4 (in mag). These optical extinctions correspond to low column densities, where most of the FUV radiation is absorbed (Hollenbach & Tielens 1999; Figure 16). We have already shown in Section 6.2.2 that the LPs have extinction values of the order of many hundreds of magnitude. Deeper within the PDR structure of Orion, corresponding to AV > 4, the Tkin/Td values decrease toward a value of unity or less (Hollenbach & Tielens 1999; Figure 16). Since we do not have values close to, or less than, Tkin/Td = 1, we can conclude that FUV heating from PDRs is likely not the primary heating mechanism in the ISM of the LPs.
)∼ 5 cm−3). These regions have a typical visual extinction AV < 4 (in mag). These optical extinctions correspond to low column densities, where most of the FUV radiation is absorbed (Hollenbach & Tielens 1999; Figure 16). We have already shown in Section 6.2.2 that the LPs have extinction values of the order of many hundreds of magnitude. Deeper within the PDR structure of Orion, corresponding to AV > 4, the Tkin/Td values decrease toward a value of unity or less (Hollenbach & Tielens 1999; Figure 16). Since we do not have values close to, or less than, Tkin/Td = 1, we can conclude that FUV heating from PDRs is likely not the primary heating mechanism in the ISM of the LPs.
Other forms of heating mechanisms, therefore, seem to be required for the more intense star-forming galaxies like the LPs. Rosenberg et al. (2014) introduce an additional form of mechanical heating38
to their PDR models in order to fit the observed line SED for the local starburst galaxy, NGC 253. In fact, this mechanical heating term is required to account for more than two-thirds of the observed mid- to high-J CO line fluxes. It is also required to recover the solutions to their alternative LVG models, one of which corresponds to a molecular phase with log( ) > 3.5 cm−3 and Tkin = 60 K. The PDR models alone could only reproduce a maximum gas kinetic temperature of 18 K when considering the gas density for the LVG model as a PDR input value. They argue that the radiation field required to heat the gas photodissociates the CO molecules in the PDR in these models, and the result is a factor of three lower value for the gas kinetic temperature between the PDR and LVG model results. Rosenberg et al. (2014) therefore argue that there is a need for this additional mechanical form of heating. Rosenberg et al. (2014) do not fit for the dust temperature and Tkin simultaneously, so there is no direct comparison to our modeling procedure. Nevertheless, it is clear that PDRs are physically unlikely to be able to excite the observed line fluxes for the LPs. This is because the LPs have dust temperatures higher than the PDR-derived, maximum gas kinetic temperature of 18 K (in the case of log(
) > 3.5 cm−3 and Tkin = 60 K. The PDR models alone could only reproduce a maximum gas kinetic temperature of 18 K when considering the gas density for the LVG model as a PDR input value. They argue that the radiation field required to heat the gas photodissociates the CO molecules in the PDR in these models, and the result is a factor of three lower value for the gas kinetic temperature between the PDR and LVG model results. Rosenberg et al. (2014) therefore argue that there is a need for this additional mechanical form of heating. Rosenberg et al. (2014) do not fit for the dust temperature and Tkin simultaneously, so there is no direct comparison to our modeling procedure. Nevertheless, it is clear that PDRs are physically unlikely to be able to excite the observed line fluxes for the LPs. This is because the LPs have dust temperatures higher than the PDR-derived, maximum gas kinetic temperature of 18 K (in the case of log( ) = 3.5 cm−3). We therefore infer that the Tkin/Td parameter reflects a strong mechanical heating mechanism within the molecular ISM of the LPs, despite the fact that our model inexplicably accounts for the source of this mechanical energy.
) = 3.5 cm−3). We therefore infer that the Tkin/Td parameter reflects a strong mechanical heating mechanism within the molecular ISM of the LPs, despite the fact that our model inexplicably accounts for the source of this mechanical energy.
Figure 17 compares the Tkin/Td parameter to the ratio of the total IR luminosity to molecular gas mass (i.e., a proxy of SFR per unit gas mass, hereafter SF efficiency, "SFE"). The SFE is believed to strongly increase with increasing redshift, accompanied by a similarly strong evolution in the mass accretion rate for field galaxies at z > 1 (Scoville et al. 2017a; Tacconi et al. 2020), as well as increased turbulent velocity dispersions and supernova (SN) rates (Joung et al. 2009; Krumholz et al. 2018). The combined feedback from various stellar evolution processes is likely captured in the SFE parameter; therefore, we expect that the value of Tkin/Td will increase with higher values of SFE. The left-hand side of Figure 17 shows some of the LPs approaching the limits of a maximal starburst.39 Overall there is a range of values for the SFE of the LPs, corresponding to galaxies that would be considered main-sequence z ∼ 2–3 star-forming galaxies, as well as the extreme outlier starburst galaxies (e.g., Genzel et al. 2010, 2015; Tacconi et al. 2018, 2020). Higher values of the IR luminosity are proportional to the increase in SFR and may therefore be an indicator for the mechanical energy input required to increase the values of Tkin/Td. Indeed, Figure 17 shows that as the SFE proxy increases, there are more LPs with higher values of Tkin/Td. The increased SFR in the LPs is expected to contribute a significant amount of energy from stellar feedback, in the form of massive protostellar outflows and/or SN explosion shocks (Norman & Silk 1980; McKee 1989; Draine & McKee 1993; Krumholz et al. 2006, 2009a; Nakamura & Li 2007; Hopkins et al. 2011; Seifried et al. 2017; Haid et al. 2018, 2019; Keller et al. 2020; Leung et al. 2020)—all of which dissipate energy through a turbulent energy cascade toward smaller physical scales (Dobbs & Pringle 2013; Van Loo et al. 2013). The LPs have a significant quantity of molecular gas; therefore, we expect that this will dominate over the radiation pressure within the ISM.40 Therefore, we expect that mechanical stellar feedback (rather than radiative feedback) will likely have a strong contribution to the pervasive turbulent gas conditions within the ISM (Jacquet et al. 2011; Krumholz et al. 2012).
Figure 17. Left: Tkin/Td parameter vs. the SF efficiency proxy, i.e., the total IR luminosity to molecular ISM mass ratio, LIR/MISM, derived using the Turbulence model, with the derived mean H2 gas density in the color bar axis (log-x scale). Right: turbulent ram pressure vs. the IR luminosity surface density, with the molecular gas mass surface density in the color bar axis (log–log scale). Both plots report the total χ2-weighted parameter mean and standard deviation values derived from the ∼2 million model calculations.
Download figure:
Standard image High-resolution imageThe total wind energy of an O-type star on the main sequence of stellar evolution, combined with the rapid mass-loss rate of the more transient Wolf–Rayet evolutionary stage, results in a fiducial range of ∼1049–51 erg in a 5 Myr lifetime (Leitherer et al. 1999; Chu 2005; Smith 2014; Ramachandran et al. 2019). As a reference, the intense star-forming region traced by the supergiant shell within IC 2574, a nearby dwarf galaxy, has an estimated kinetic energy input of the order of ∼3 × 1053 erg over a 1 Myr lifetime (Walter et al. 1998). We can estimate the stellar mechanical wind energy input using a fiducial value for the intrinsic SFR for the LPs of 1000 M⊙ yr−1 (see also Section 6.2.2) and an expected cumulative fraction of 0.2% by number for massive stars (Kroupa initial mass function; Kroupa 2002).41 The approximate stellar mechanical wind energy input is of the order of ∼1 × 1058−59 erg. SN events occur at the end of the life cycle of massive stars with initial stellar masses between ∼10 and 40 M⊙ (Heger et al. 2003), each of which produces roughly 1051 erg (Jones et al. 1999). If we assume that these massive stars consist of ∼7% of the total stellar mass fraction, we derive an SN rate of ∼6 SN yr−1 for the LPs, which is ∼300× the value of the Milky Way (Diehl 2011). For reference, the center of M82 has an estimated rate of ∼0.1 SN yr−1 (Kronberg et al. 1981; Weiß et al. 1999).
We can further estimate the energy input from SNe to be on the order of 1059 erg using the reference time frame of 70 Myr. Therefore, this value is an upper limit, since we do not expect that the injection of energy from SNe will be a continuous process. Nonetheless, this value is comparable to our simplistic estimate of the possible stellar mechanical wind energy input from young massive stars over 70 Myr, which are expected to provide a steady stream of mechanical energy throughout their lifetimes via stellar winds with terminal velocities of the order of 1000 km s−1 (Conti et al. 1988; Puls et al. 2008). The direct impact of massive stars and SNe, however, may be biased toward their most immediate environments. It has also been shown theoretically that only a 1% fraction, or less, of the SN energy output is transformed into turbulent energy (Iffrig & Hennebelle 2015; Martizzi et al. 2016). Overall, the mixture of both SN events occurring in parallel with the stellar evolution processes of the population of Wolf–Rayet stars and short-lived massive stars in young stellar associations can still potentially provide a large fraction of the necessary energy budget with respect to the value of  erg. In addition, the mechanical energy of E(massive stellar winds and SNe) ∼ 1059–60 erg.
erg. In addition, the mechanical energy of E(massive stellar winds and SNe) ∼ 1059–60 erg.
Despite the potentially strong energetic contributions from stellar evolution processes, massive stars may not be the only sources of such turbulent energy input. Gravity may play an equally important role in introducing a large amount of turbulent gas motion, which may sustain the relatively high turbulent velocity dispersions we derived for the LPs. The right-hand side of Figure 17 shows the relationship between the IR luminosity surface density,  , and the turbulent ram pressure for the LPs. The equivalent turbulent gas ram pressure is connected to the vertical stabilizing force in a marginally stable gas disk. This pressure will increase as the SF activity increases, according to turbulence-regulated SF models (Krumholz et al. 2009b, 2018; Bournaud et al. 2010). We use the mean values from the Turbulence model to calculate the turbulent ram pressure to be Pturb =
, and the turbulent ram pressure for the LPs. The equivalent turbulent gas ram pressure is connected to the vertical stabilizing force in a marginally stable gas disk. This pressure will increase as the SF activity increases, according to turbulence-regulated SF models (Krumholz et al. 2009b, 2018; Bournaud et al. 2010). We use the mean values from the Turbulence model to calculate the turbulent ram pressure to be Pturb =  = 106.2–9.8 (km s−1)2 cm−3, which is significantly higher than the gas thermal pressure, Pth = P/k = n(H2) × Tkin = 102.9–6.9 K cm−3 (with k the Boltzmawnn constant). Many LPs have large uncertainties due to our lack of constraints on the molecular gas density and our total errors, and future work may refine these values for individual LPs using spatially resolved line measurements of the mean turbulent velocity dispersion. Both the Kendall's tau statistic τ = 0.27 and the Spearman's rank correlation r = 0.37 indicate that there is only a mild positive correlation with the turbulent gas pressure across the range of
= 106.2–9.8 (km s−1)2 cm−3, which is significantly higher than the gas thermal pressure, Pth = P/k = n(H2) × Tkin = 102.9–6.9 K cm−3 (with k the Boltzmawnn constant). Many LPs have large uncertainties due to our lack of constraints on the molecular gas density and our total errors, and future work may refine these values for individual LPs using spatially resolved line measurements of the mean turbulent velocity dispersion. Both the Kendall's tau statistic τ = 0.27 and the Spearman's rank correlation r = 0.37 indicate that there is only a mild positive correlation with the turbulent gas pressure across the range of  ∼ 1011–12 L⊙ kpc−2 for the LPs, if any. Since there is a large amount of turbulent energy present in the LPs, it is inferred that the thermal pressure equilibrium of clouds is negligible overall in terms of regulating the SF activity. This result is consistent with theoretical studies (e.g., Ballesteros-Paredes et al. 1999). It is important to measure the mean molecular gas thermal pressure, as it sets the background for thermal pressure balance throughout the ISM, as galaxies with higher than 50% molecular gas to atomic gas fractions are subject to collapse (Krumholz & McKee 2005).
∼ 1011–12 L⊙ kpc−2 for the LPs, if any. Since there is a large amount of turbulent energy present in the LPs, it is inferred that the thermal pressure equilibrium of clouds is negligible overall in terms of regulating the SF activity. This result is consistent with theoretical studies (e.g., Ballesteros-Paredes et al. 1999). It is important to measure the mean molecular gas thermal pressure, as it sets the background for thermal pressure balance throughout the ISM, as galaxies with higher than 50% molecular gas to atomic gas fractions are subject to collapse (Krumholz & McKee 2005).
Our results indicate that the additional form of turbulent pressure is an important form of feedback to regulate the intense SF activity for these gas-rich LPs. Using Equation (A7) from Brucy et al. (2020) for the upper bound for possible turbulent power, ΠSNe, injected by an SN,
This yields a much lower estimate of the total turbulent energy input from SNe over the 70 Myr of ∼1056 erg, still ∼3 orders of magnitude less than  . This equation assumes that the turbulence energy injection is proportional to the surface-integrated SFR (Krumholz et al. 2018; Brucy et al. 2020). The high gas mass surface densities of the LPs can therefore produce much more power from stellar feedback than the highest explored values for the SFR ∼ 100 M⊙ yr−1 in the work of Brucy et al. (2020); therefore, these estimates may reflect lower limits. Brucy et al. (2020) find that the large-scale turbulent energy injection has a much higher dependence on the gas mass surface densities, by almost three orders of magnitude. The general scenario is consistent with other studies, which find a more dominant turbulent energy contribution from large-scale motions instead of pure stellar feedback (Bournaud et al. 2010; Renaud et al. 2012; Colling et al. 2018; Krumholz et al. 2018). We can loosely estimate this large-scale turbulent energy input based on the theoretical model values of Brucy et al. (2020) for a dense molecular medium, corresponding to ∼1040 erg s−1. We calculate, over 70 Myr, an estimate of ∼1055 erg. This is one order of magnitude higher than the fiducial Eturb ∼ 1054–55 erg we estimate above for the LPs. Therefore, a substantial amount of turbulence energy can also be supplied from large-scale disk motions.
. This equation assumes that the turbulence energy injection is proportional to the surface-integrated SFR (Krumholz et al. 2018; Brucy et al. 2020). The high gas mass surface densities of the LPs can therefore produce much more power from stellar feedback than the highest explored values for the SFR ∼ 100 M⊙ yr−1 in the work of Brucy et al. (2020); therefore, these estimates may reflect lower limits. Brucy et al. (2020) find that the large-scale turbulent energy injection has a much higher dependence on the gas mass surface densities, by almost three orders of magnitude. The general scenario is consistent with other studies, which find a more dominant turbulent energy contribution from large-scale motions instead of pure stellar feedback (Bournaud et al. 2010; Renaud et al. 2012; Colling et al. 2018; Krumholz et al. 2018). We can loosely estimate this large-scale turbulent energy input based on the theoretical model values of Brucy et al. (2020) for a dense molecular medium, corresponding to ∼1040 erg s−1. We calculate, over 70 Myr, an estimate of ∼1055 erg. This is one order of magnitude higher than the fiducial Eturb ∼ 1054–55 erg we estimate above for the LPs. Therefore, a substantial amount of turbulence energy can also be supplied from large-scale disk motions.
Due to the conservation of angular momentum, any form of momentum injection into the molecular cloud surroundings will likely be radially transported toward the gravitational center of the galaxy. Indeed, mass accretion may play a primary role in increasing the level of turbulent energy within the ISM during these starburst episodes (Schmidt et al. 2016).42 The kiloparsec-scale dynamics for these high-z gas-rich star-forming galaxies cause gravitational instabilities, and the turbulent driving from these processes may be a primary source of the bulk kinetic energy density (Silk 1997; Schmidt et al. 2009; Bournaud et al. 2010; Krumholz & Burkhart 2016; Colling et al. 2018; Krumholz et al. 2018; Brucy et al. 2020). These single-dish measurements offer a global view, or "top-down" perspective, of the molecular ISM conditions within the LPs. The gas mass surface density drives these high SFR and IR luminosity surface densities in "top-down" processes (Krumholz et al. 2018). The extreme gas mass surface densities may help to explain the extreme intrinsic IR luminosities exceeding 1013 L⊙.
We expect that such massive galaxy-wide SF will act to restabilize the forming disk over a timescale of ∼100 Myr; meanwhile, fresh gas is likely to be accreted, consumed, or displaced within the ISM and/or in the form of massive galactic outflows (Quirk & Tinsley 1973; Cox 1981; Dopita et al. 1985; Larson 1987; Ostriker et al. 2010; Veilleux et al. 2020). Altogether, such arguments for turbulence-regulated SF are consistent with evidence presented for both local (U)LIRGs and high-z starbursts. The local (U)LIRGs, with similar CO line SED coverage, require high amounts of mechanical energy/turbulent activity to sustain the higher-J CO line emission (e.g., Tacconi et al. 1999; Lu et al. 2014; Kamenetzky et al. 2016), while the 10 kpc scale turbulent molecular gas reservoirs are believed to extend the starburst phase of high-z star-forming galaxies through the interplay of stellar/AGN feedback and intergalactic gas accretion (Falgarone et al. 2017).
8. Conclusions
In this work we have studied the physical gas properties of the molecular and atomic ISM at high z. We have measured and compiled a compendium of roughly 200 CO and [C i] spectral lines measured in a sample of 24 strongly lensed star-forming systems at z ∼ 1–4, selected from the all-sky sub/millimeter Planck satellite (the LPs). To yield deeper insight into the molecular ISM excitation conditions, we systematically measured the multi-J line excitation of CO and [C i] using spatially unresolved, single-dish observations (i.e., IRAM 30 m ([C i] and CO (Jup = 3–11)), GBT (CO (1−0)), and APEX ([C i] and CO (Jup = 4–12))).
This work is the first major effort to simultaneously fit all of the available spectral line and dust continuum observations. The vast majority of previous high-z studies have focused on non-LTE radiative transfer modeling of a single- or double-component model of the observed line emission, excluding the thermal background from the IR radiation field. In this work we perform two complementary modeling procedures to model all of the line/continuum data: (i) a two-component molecular medium model, which enabled us to highlight the dominant properties of the more diffuse/quiescent and denser/highly excited gas; and (ii) a more realistic description of a molecular ISM that is described by a turbulence-driven, molecular gas density pdf. Our main results are summarized as follows:
- 1.The broad [C i] and CO lines (
 km s−1) are strikingly similar in line shape; therefore, these emission lines trace comparable galactic dynamics across the spatially unresolved, kiloparsec scales.
km s−1) are strikingly similar in line shape; therefore, these emission lines trace comparable galactic dynamics across the spatially unresolved, kiloparsec scales. - 2.We have derived the mean CO line brightness temperature ratios for the LPs out to the ratio of
 , based on our best-fit, minimum-χ2 Turbulence model. In addition, we have derived a set of median CO line brightness temperature ratios for a significant number of z = 1–7 galaxies with CO line detections, including the compilations by Carilli & Walter (2013) and Kirkpatrick et al. (2019). Although the median values are in excellent agreement with the average best-fit, minimum-χ2 model-derived values for the LPs, the wide range in CO excitation observed in individual galaxies implies that the use of an average (or median-based) value used for scaling
, based on our best-fit, minimum-χ2 Turbulence model. In addition, we have derived a set of median CO line brightness temperature ratios for a significant number of z = 1–7 galaxies with CO line detections, including the compilations by Carilli & Walter (2013) and Kirkpatrick et al. (2019). Although the median values are in excellent agreement with the average best-fit, minimum-χ2 model-derived values for the LPs, the wide range in CO excitation observed in individual galaxies implies that the use of an average (or median-based) value used for scaling  measurements may be misleading when there are limited line/continuum data available.
measurements may be misleading when there are limited line/continuum data available. - 3.There is a wide range in the observed intensities for the CO rotational ladder, with an order-of-magnitude dispersion tracing a range of gas excitation in these lensed IR-luminous, star-forming galaxies. We further explored this wide dynamic range in observed gas excitation following the methodology presented by Rosenberg et al. (2015) for local IR-luminous galaxies. We have thereby classified the CO excitation ladder with respect to the drop-off slope after the CO (5−4) transition by taking the ratio of the higher-J CO line luminosities to the mid-J CO line luminosities and find that the LPs probe more than 4 orders of magnitude in CO excitation. This classification increases to higher excitation as the derived FIR luminosity increases.
- 4.There are 19 LPs with a [C i] line detection, while 16 have both [C i] lines detected. Our non-LTE radiative transfer modeling of these lines suggests that the [C i] lines are indeed optically thin, which is important for reliable calibrations to carbon gas column density and total mass. The two ground-state fine-structure carbon lines are subthermally excited, however. We demonstrate, using 16 LPs with both [C i] line detections, that the often-assumed LTE approximation to derive the carbon excitation temperature may under- or overestimate the intrinsic carbon excitation temperature, depending on the gas excitation conditions of individual galaxies. We derived mean carbon gas excitation temperatures Texc ∼ 30 and 40 K for the Turbulence model and 2-component model, respectively. In some of the LPs we find values less than 20 K, and we would have misinterpreted the inferred total molecular gas mass if we had assumed the ideal, LTE prescription. We find, for the Turbulence model, the sample mean for the LPs of
![$\langle [[{\rm{C}}\,{\rm\small{I}}]]/[{{\rm{H}}}_{2}]\rangle \,\sim 6.8\times {10}^{-5}$](data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAAEAAAABCAQAAAC1HAwCAAAAC0lEQVR42mNkYAAAAAYAAjCB0C8AAAAASUVORK5CYII=) , with a large dispersion.
, with a large dispersion. - 5.The average intrinsic size of the modeled gas- and dust-emitting region for the Turbulence model was derived to be
 . We have estimated the mean magnification using all of the available ranges derived for the LPs that have lens models. For the LPs without published magnification factors, we provide an estimate using the "Tully–Fisher" argument method presented by Harris et al. (2012) and our novel CO (1−0) line measurements. The intrinsic size for individual LPs based on detailed lens modeling agrees well with the expected intrinsic size derived in our modeling.
. We have estimated the mean magnification using all of the available ranges derived for the LPs that have lens models. For the LPs without published magnification factors, we provide an estimate using the "Tully–Fisher" argument method presented by Harris et al. (2012) and our novel CO (1−0) line measurements. The intrinsic size for individual LPs based on detailed lens modeling agrees well with the expected intrinsic size derived in our modeling. - 6.We derived total molecular ISM masses in our modeling of the observed CO/[C i] lines and dust SED. Both of the modeling procedures are consistent in deriving MISM, yet we find systematic offsets, as the single-band 1 mm dust continuum method overpredicts the MISM derived using our robust modeling procedures. Our derived mean, mass-weighted Td ∼ 40 K for the sample of LPs does not suggest the use of the recommended mass-weighted Td = 25 K value when using a ∼1 mm dust continuum observation to estimate the total molecular ISM mass. In fact, both of the modeling procedures indicate that the mass-weighted and luminosity-weighted Td are close to identical, on average.
- 7.We find a wide range in CO luminosity per mass, with a mean close to the Galactic value, i.e., αCO ∼ 3.4 M⊙ (K km s−1 pc2)−1; however, there is a large dispersion. Each system has a unique value of αCO, disfavoring the use of a single value common for active star-forming galaxies at high z. Our modeling suggests that the value of αCO increases with increasing gas mass surface density, as well as with gas volume density. The value of αCO decreases toward unity or less for increasing gas kinetic temperatures, specifically Tkin > 120 K.
- 8.The more realistic description of the turbulent molecular gas offers a picture of the excitation conditions of the ISM in the LPs. The large emitting regions are highly turbulent, as inferred by their mean turbulent velocity dispersion (ΔVturb > 125 km s−1), and the gas kinetic temperature to dust temperature ratios Tkin/Td > 2.5, on average, suggest that the LPs require a significant amount of mechanical activity on >kiloparsec scales (the driving scale) in conjunction with their massive molecular gas reservoirs. Since the inferred gas depletion time, MISM/SFR, is of the order of 70 Myr, there must be a significant amount of gas, likely supplied from the CGM over the lifetime of this ∼100 Myr starburst episode. The Tkin/Td ratio also increases with the inferred SF efficiency (i.e., LIR/MISM), which suggests that the kinetic input from increased SNe and stellar winds may also play a role in characterizing the overall mechanical heating in the ISM.
We would like to sincerely thank the anonymous reviewer for their insightful and thoughtful comments that have influenced the quality of the manuscript. K.C.H. would like to acknowledge the useful discussions to improve this manuscript with Nick Scoville, Alexandra Pope, Mark Krumholz, Stefanie Mühle, Tom Bakx, and Chentao Yang. K.C.H. would wholeheartedly like to thank all telescope station managers, operators, and shift observers at all facilities: Carsten Kramer, Ignacio Ruiz, Manuel Ruiz, Frederic Damour, Joaquin Santiago, Kika, Victor Puela, Santiago Navarro, Salvador Sanchez, Martin Steinke, Jonathan Braine, Ivan Agudo, Maria Nuria Marcelino Lluch, Zsofia Nagy, Francesco Fontani, Elena Redaelli, Amber Bonsall, Amanda Jo, Toney Minter, Karen O'Neil, Rodrigo Parra, Mungo Jerry, Francisco Azagra, Felipe Mac-Auliffe, Paulina Vasquez, Eduoardo Gonzalez, Mauricio Martinez, Juan-Pablo Perez-Beapuis, Arnoud Belloche, Friedrich Wyrowski, Papito, Arshia Jacob, Parichay Mazumdar, Nina Brinkmann, and Hans Nguyen. This work is carried out within the Collaborative Research center 956, subproject [A1, C4], funded by the Deutsche Forschungsgemeinschaft (DFG). T.K.D.L. acknowledges funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation program (grant agreement No. 694343). A.D.S. acknowledges support from project PID2019-110614GB-C22 (MICINN). The research leading to these results has received funding from the European Union's Horizon 2020 research and innovation program under grant agreement No. 730562 [RadioNet]. This publication is based on data acquired with the Atacama Pathfinder Experiment (APEX) Telescope. APEX is a collaboration between the Max-Planck-Institut fur Radioastronomie, the European Southern Observatory, and the Onsala Space Observatory. This publication also makes use of the Green Bank Observatory, a facility of the National Science Foundation operated under cooperative agreement by Associated Universities, Inc. This work is also based on observations carried out with the IRAM 30 m telescope. IRAM is supported by INSU/CNRS (France), MPG (Germany), and IGN (Spain). This research has made use of NASA's Astrophysics Data System. This research has made use of adstex (https://github.com/yymao/adstex).
Facilities: GBT:100 m - , IRAM:30 m - , APEX:12 m. -
Appendix A: Notes on Differential Lensing
The total size of the emitting region of the low-excitation and higher-excitation emission lines of CO may vary intrinsically in the source plane; therefore, if these emitting regions are disproportionately distributed along the caustic, the observed fluxes could yield differential magnifications. That is, the more compact emission traced by higher-J CO transitions may be magnified by a factor that is significantly different from the diffuse, low-excitation gas (Blain 1999; Hezaveh et al. 2012; Serjeant 2012), if it lies closer, on average, to the caustic. As AGNs/QSOs have extreme luminosities centrally located within the host galaxy, these point-like objects may be subject to stronger differential lensing than starburst galaxies. This would lower the probability that such a distinction is made between the magnification factor for higher-J CO versus the low-J CO-emitting regions. This is because the source of the higher-J emission in AGN/QSOs is likely confined to a concentrated region near the center of mass of the host galaxy, whereas the starburst galaxies have more extended reservoirs that may be well mixed, and both low-J and high-J lines may be magnified differentially in a similar manner, on average. Differential lensing may be more pronounced when comparing low- and high-J CO line fluxes; however, the bulk of this work is focused on global properties such as the total molecular gas mass—which is most sensitive to the lowest-J CO line measurements. High angular resolution imaging in the future is required to investigate differential lensing. We therefore focus on the observed quantities.
Due to the extreme starburst nature of the LPs, the molecular ISM may have a large volume filling factor of gas, suggesting a smooth distribution of SF on galactic scales (Kennicutt 1998; Kennicutt & Evans 2012). An explicit accounting of this would require assigning a unique magnification factor to each measurement of the dust continuum and a magnification factor per velocity channel for the CO/[C i] lines to model the de-magnified integrated fluxes (see, e.g., Leung et al. 2017). Recent studies have shown a similar magnification factor for the low-J CO/adjacent dust continuum (Cañameras et al. 2017a, 2018b), while others show a nonnegligible 20%–40% differential magnification of low- to mid-J CO/dust continuum (Yang et al. 2019). It is clear that every lens configuration is a unique system, and therefore a coherent set of lens models is required for the lower-excitation versus the higher-excitation molecular/atomic gas at matching spatial resolution and signal-to-noise ratio (S/N) to diagnose these effects more systematically. However, in this study the effective source radius, described below, is directly connected to the apparent flux within the source solid angle and is used as input to the model. For our two-component modeling, we cannot explicitly determine the differential lens magnification factor, as the intrinsic ratio of the emitting radius for each component may be different from the modeled ratio. Thirteen out of the 24 LPs presented here have lens models developed based on a wide range of high angular resolution HST near-IR data and/or ground-based optical/near-IR follow-up of the foreground and lensing environment (Díaz-Sánchez et al. 2017; Frye et al. 2019). A small subset of the LPs have a range of marginally resolved to highly resolved (down to beam sizes, θ ∼ 0 1–0
1–0 2) millimeter–radio interferometric dust continuum and/or single-line CO imaging to also aid lens modeling efforts (Bussmann et al. 2015; Geach et al. 2015, 2018; Cañameras et al. 2017a, 2017b, 2018a). Overall, these systems have flux-weighted total magnification factors ranging between 10 and 40 (Table 1).
2) millimeter–radio interferometric dust continuum and/or single-line CO imaging to also aid lens modeling efforts (Bussmann et al. 2015; Geach et al. 2015, 2018; Cañameras et al. 2017a, 2017b, 2018a). Overall, these systems have flux-weighted total magnification factors ranging between 10 and 40 (Table 1).
The lack of magnification factor estimates derived for each of the emission lines, in addition to multiple magnification factor estimates derived from sampling the rest-FIR thermal continuum emission, restrict our analyses to the magnified (apparent) quantities. Harris et al. (2012) used a "Tully–Fisher" line luminosity/line width relation to offer an empirical perspective on estimating the unknown magnification of the CO (1−0) line measured in 24 Herschel-selected, strongly lensed galaxies. There may be an intrinsic dispersion among the LPs along this empirical relation, and the inclination angle is unaccounted for, yet we can use Equation (2) of Harris et al. (2012) to estimate the lens magnification factor based on our GBT detected CO (1−0) line measurements. We derive the line FWHM using a simple 1D Gaussian model fit to the velocity line profiles as done by Harrington et al. (2018). In the case of LPsJ0305, LPsJ0226, LPsJ105353, and LPsJ112713, there are no available CO (1−0) line data. Therefore, we use the value of  from the best-fit, minimum-χ2 Turbulence model and the measured FWHM from the low-J CO line data. We report the derived magnification factors in Table 1. This magnification factor estimate, which is usually 1.5–3× higher than previously reported results, has systematic uncertainties in estimating the lens magnification estimate that could be more than 50% based on the intrinsic scatter within the calibration sample used in Harris et al. (2012).
from the best-fit, minimum-χ2 Turbulence model and the measured FWHM from the low-J CO line data. We report the derived magnification factors in Table 1. This magnification factor estimate, which is usually 1.5–3× higher than previously reported results, has systematic uncertainties in estimating the lens magnification estimate that could be more than 50% based on the intrinsic scatter within the calibration sample used in Harris et al. (2012).
Appendix B: Turbulence Model Posterior Distributions
In Section 5.4 we discuss our optimization fitting procedure, for which we employ a Markov Chain process combined with the optimization routine to sample the underlying probability distribution of each parameter (see Pham & Castellani 2009; Strandet et al. 2017, and future work). In Figure 18 we show an example, for LPsJ1323, of the likelihood-weighted posterior distributions for the explored range of parameters (Table 3), corresponding to ∼2 million model calculations. As noted in Section 5.4, the average galaxy-integrated gas excitation conditions of the LPs are inferred based on the mean, likelihood-weighted parameters (as determined by the χ2 value) and uncertainties, which encompass a wide variation in solution space (Figure 18). The highest-likelihood regions in Figure 18 correspond to the best-fit, minimum χ2 solutions used as input parameters to calculate the best-fit models to match the observed line/continuum SEDs, as seen in Figure 4.
Figure 18.
Posterior likelihood distributions within the explored solution space for the parameters used in the Turbulence model. Denser regions indicate model calculations with higher likelihood. Note that the gas density is in log10 units. The range of parameters corresponds to the tightened parameter limits described in the text (see Table 3). Contours represent the 16th and 84th percentiles. The red points indicate the likelihood-weighted mean and standard deviation as based on ∼2 million model calculations. The general parameter space degeneracy observed here between parameters reflects many of the same features for the other LPs; the corresponding posterior distributions can be found online. (The complete figure set (24 images) is available.)
Download figure:
Standard image High-resolution imageAppendix C: Tabulated Properties
This section includes tabulated properties for both the observational measurements and model fits.
C.1. Observations and Line Measurements
This section presents observations and line measurements in Tables 6–9.
Table 6. Summary of Observations
| Source ID | Line ID | Receiver | Date of Observation | Mean Tsys | Int. Time | νobs | Error νobs | Gain | rms |
|---|---|---|---|---|---|---|---|---|---|
| (d:m:y) | (K) | (minutes) | (GHz) | (GHz) | (Jy K−1) | (Jy km s−1) | |||
| LPsJ0116 | CO (1−0) | Ka band | 20.10.17 | 170 | 60 | 36.88243 | 0.00184 | 1.60 | 0.041 |
| CO (6−5) | PI230 | 30.05.18 | 91 | 128 | 221.31994 | 0.01107 | 41.50 | 0.984 | |
| [C i] (2−1) | PI230 | 28.05.18 | 123 | 355 | 259.02220 | 0.01295 | 43.00 | 0.615 |
Note. The rms sensitivity is calculated as the integrated flux (Jy km s−1) within ΔV ≈ 500–1000 km s−1 (channel width ∼80–110 km s−1). Integration time corresponds to the averaged scans used for analysis. Also note that a few detected lines in this work were previously reported in the literature (Cañameras et al. 2018b; Nesvadba et al. 2019), but we present deeper (5–10× better S/N) observations for those ∼20 CO/[C i] lines. Duplicate line measurements include LPsJ105353 (CO (5−4), CO (6−5), CO (8−7), CO (9−8)), LPsJ112714 (CO (4−3), CO (7−6), [C i] (2−1)), LPsJ1202 (CO (4−3), CO (5−4), CO (7−6), [C i] (1−0), [C i] (2−1)), LPsJ1323 (CO (4−3), CO (5−4), CO (7−6), [C i] (1−0), [C i] (2−1)), and LPsJ1609 (CO (5−4), CO (6−5), CO (8−7), CO (9−8)) (Cañameras et al. 2018b; Nesvadba et al. 2019).
A machine-readable version of the table is available.
Download table as: DataTypeset image
Table 7. Measured Line Properties
| ID | Jup | Line ID | Redshift | ErrRedshift | Sν ΔV | ErrSν ΔV | L' | ErrL' | Llin | ErrLlin | Lower Bound | Upper Bound |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (Jy km s−1) | (Jy km s−1) | (×1010 K km s−1 pc2) | (×1010 K km s−1 pc2) | (×108 L⊙) | (×108 L⊙) | (km s−1) | (km s−1) | |||||
| LPsJ0116 | 1 | CO (1−0) | 2.12537 | 1.34E−04 | 4.68 | 1.64 | 1.06E+02 | 3.72E+01 | 5.22E−01 | 1.83E−01 | −300 | 500 |
| LPsJ0116 | 3 | CO (3−2) | 2.12490 | 1.34E−04 | 51.10 | 10.22 | 1.29E+02 | 2.58E+01 | 1.71E+01 | 3.42E+00 | −500 | 500 |
| LPsJ0116 | 6 | CO (6−5) | 2.12431 | 1.34E−04 | 55.20 | 16.56 | 3.49E+01 | 1.05E+01 | 3.69E+01 | 1.11E+01 | −200 | 650 |
| LPsJ0116 | 7 | CO (7−6) | 2.12443 | 1.34E−04 | 33.25 | 9.98 | 1.54E+01 | 4.63E+00 | 2.59E+01 | 7.78E+00 | −300 | 500 |
| LPsJ0116 | 8 | CO (8−7) | 2.12398 | 1.34E−04 | 30.34 | 10.62 | 1.08E+01 | 3.77E+00 | 2.70E+01 | 9.46E+00 | −250 | 500 |
| LPsJ0116 | 9 | CO (9−8) | 2.12417 | 1.34E−04 | 19.72 | 6.90 | 5.54E+00 | 1.94E+00 | 1.97E+01 | 6.91E+00 | −250 | 200 |
| LPsJ0116 | 2 | [C i] (2−1) | 2.12443 | 1.34E−04 | 31.34 | 9.40 | 1.44E+01 | 4.33E+00 | 2.45E+01 | 7.35E+00 | −1200 | −550 |
Note. All observations reported in Table 6 were used to derive the line-integrated measurements (full width at zero intensity, FWZI) within the integral regions marked above.
Only a portion of this table is shown here to demonstrate its form and content. A machine-readable version of the full table is available.
Download table as: DataTypeset image
Table 8. Best-fit Turbulence Model Line Properties
| Source ID | Jup | Sν ΔV |
|
LCO | R(Jup, 1) |
|---|---|---|---|---|---|
| (Jy km s−1) | (1010 K km s−1 pc2) | (108 L⊙) | |||
| LPsJ0116 | 1 | 6.37E+00 | 1.45E+02 | 7.10E−01 | 1.00E+00 |
| 2 | 2.18E+01 | 1.24E+02 | 4.85E+00 | 8.55E−01 | |
| 3 | 3.80E+01 | 9.61E+01 | 1.27E+01 | 6.64E−01 | |
| 4 | 4.89E+01 | 6.95E+01 | 2.18E+01 | 4.80E−01 | |
| 5 | 5.22E+01 | 4.75E+01 | 2.91E+01 | 3.28E−01 | |
| 6 | 4.84E+01 | 3.06E+01 | 3.24E+01 | 2.11E−01 | |
| 7 | 4.00E+01 | 1.86E+01 | 3.12E+01 | 1.28E−01 | |
| 8 | 2.94E+01 | 1.05E+01 | 2.62E+01 | 7.23E−02 | |
| 9 | 1.89E+01 | 5.32E+00 | 1.90E+01 | 3.68E−02 | |
| 10 | 1.03E+01 | 2.35E+00 | 1.15E+01 | 1.62E−02 | |
| 11 | 4.60E+00 | 8.66E−01 | 5.64E+00 | 5.98E−03 | |
| 12 | 1.50E+00 | 2.37E−01 | 2.00E+00 | 1.64E−03 | |
| 13 | 3.09E−01 | 4.16E−02 | 4.47E−01 | 2.87E−04 | |
| 14 | 4.87E−02 | 5.66E−03 | 7.58E−02 | 3.91E−05 | |
| 15 | 6.08E−03 | 6.16E−04 | 1.02E−02 | 4.26E−06 |
Note. Best-fit CO excitation ladders, as determined from the best model solution in the top 1% of the best χ2 solutions. The model error for each value is of order 5% based on the dispersion of best-fit values within the top solutions.
Only a portion of this table is shown here to demonstrate its form and content. A machine-readable version of the full table is available.
Download table as: DataTypeset image
Table 9. Ancillary Dust Photometry
| Source ID | Observed Frequency | Flux Density | Err. Flux Density | Telescope |
|---|---|---|---|---|
| (GHz) | (mJy) | (mJy) | ||
| LPsJ0116 | 857 | 513 | 462 | Planck |
| 545 | 555 | 336 | Planck | |
| 273 | 66 | 10 | ALMA/Band 6 |
Note. Ancillary dust photometry for the LPs.
Only a portion of this table is shown here to demonstrate its form and content. A machine-readable version of the full table is available.
Download table as: DataTypeset image
C.2. Model Fits
Table 10 presents the model-derived values for the Turbulence model.
Table 10. Mean Values for Turbulence Model Fits
| Source ID | log(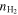 ) ) |
Err. log(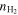 ) ) |
Tk | Err. Tk | μLReff | Err. μLReff | ΔVturb | Err. ΔVturb |
|---|---|---|---|---|---|---|---|---|
| (cm−3) | (cm−3) | (K) | (K) | (pc) | (pc) | (km s−1) | (km s−1) | |
| LPsJ0116 | 4.92E+00 | 3.82E+00 | 6.97E+01 | 3.29E+01 | 1.46E+04 | 2.48E+03 | 1.48E+02 | 3.56E+01 |
| LPsJ0209 | 5.86E+00 | 6.17E−01 | 4.34E+01 | 3.54E+00 | 1.61E+04 | 2.96E+03 | 3.58E+01 | 3.31E+01 |
| LPsJ0226 | 4.67E+00 | 4.83E+00 | 2.93E+02 | 7.32E+01 | 1.68E+04 | 3.13E+03 | 1.69E+02 | 3.42E+01 |
| LPsJ0305 | 4.76E+00 | 4.21E+00 | 1.18E+02 | 5.17E+01 | 9.33E+03 | 2.10E+03 | 1.68E+02 | 3.00E+01 |
| LPsJ0748 | 4.89E+00 | 3.79E+00 | 7.60E+01 | 2.46E+01 | 1.56E+04 | 2.42E+03 | 1.35E+02 | 3.58E+01 |
| LPsJ0846 | 4.01E+00 | 1.01E+01 | 1.06E+02 | 2.87E+01 | 1.42E+04 | 2.77E+03 | 1.45E+02 | 4.31E+01 |
| LPsJ105322 | 5.27E+00 | 7.90E−01 | 4.52E+01 | 3.68E+00 | 1.49E+04 | 2.76E+03 | 1.56E+02 | 3.85E+01 |
| LPsJ105353 | 4.05E+00 | 4.52E+00 | 1.37E+02 | 5.25E+01 | 1.45E+04 | 2.81E+03 | 9.83E+01 | 5.56E+01 |
| LPsJ112714 | 4.59E+00 | 5.39E+00 | 6.74E+01 | 4.03E+01 | 1.15E+04 | 4.21E+03 | 1.22E+02 | 5.35E+01 |
| LPsJ112713 | 3.31E+00 | 2.14E+01 | 1.41E+02 | 4.90E+01 | 1.71E+04 | 2.41E+03 | 1.09E+02 | 4.45E+01 |
| LPsJ1138 | 4.45E+00 | 5.93E+00 | 2.97E+02 | 7.68E+01 | 7.17E+03 | 2.06E+03 | 1.55E+02 | 4.32E+01 |
| LPsJ1139 | 3.71E+00 | 4.11E+00 | 5.00E+01 | 8.92E+00 | 1.34E+04 | 2.20E+03 | 1.48E+02 | 3.52E+01 |
| LPsJ1202 | 3.27E+00 | 1.29E+01 | 8.97E+01 | 2.22E+01 | 1.56E+04 | 2.26E+03 | 1.56E+02 | 3.51E+01 |
| LPsJ1322 | 4.46E+00 | 6.57E+00 | 1.58E+02 | 6.47E+01 | 1.42E+04 | 3.94E+03 | 8.14E+01 | 5.00E+01 |
| LPsJ1323 | 3.50E+00 | 1.83E+01 | 1.64E+02 | 4.70E+01 | 1.29E+04 | 2.82E+03 | 1.39E+02 | 4.32E+01 |
| LPsJ1326 | 3.01E+00 | 1.89E+01 | 9.06E+01 | 2.27E+01 | 1.54E+04 | 2.96E+03 | 1.36E+02 | 4.82E+01 |
| LPsJ1329 | 4.52E+00 | 3.77E+00 | 2.43E+02 | 7.73E+01 | 1.47E+04 | 4.30E+03 | 8.60E+01 | 5.71E+01 |
| LPsJ1336 | 4.12E+00 | 8.36E+00 | 2.05E+02 | 6.47E+01 | 1.33E+04 | 2.22E+03 | 1.53E+02 | 3.71E+01 |
| LPsJ1428 | 5.17E+00 | 1.90E+00 | 4.85E+01 | 1.78E+01 | 6.65E+03 | 2.86E+03 | 6.68E+01 | 4.47E+01 |
| LPsJ1449 | 4.79E+00 | 3.50E+00 | 6.66E+01 | 3.95E+01 | 8.82E+03 | 4.22E+03 | 1.16E+02 | 5.66E+01 |
| LPsJ1544 | 2.64E+00 | 1.41E+01 | 4.18E+01 | 6.34E+00 | 1.70E+04 | 1.63E+03 | 1.70E+02 | 2.32E+01 |
| LPsJ1607 | 5.30E+00 | 2.03E+00 | 5.24E+01 | 2.22E+01 | 9.63E+03 | 3.37E+03 | 2.98E+01 | 2.82E+01 |
| LPsJ1609 | 2.82E+00 | 1.63E+01 | 1.86E+02 | 4.61E+01 | 1.80E+04 | 1.69E+03 | 1.48E+02 | 3.48E+01 |
| LPsJ2313 | 5.43E+00 | 1.82E+00 | 9.02E+01 | 4.40E+01 | 1.34E+04 | 2.53E+03 | 1.33E+02 | 4.15E+01 |
| Source ID | κvir | Err, κvir | δv/δr | Err, δv/δr | Tk/Td | Err, Tk/Td | Td | Err, Td |
|---|---|---|---|---|---|---|---|---|
| (—) | (km s−1 pc−1 cm3/2) | (km s−1 pc−1cm3/2) | (km s−1 pc−1) | (km s−1 pc−1) | (—) | (—) | (K) | (K) |
| LPsJ0116 | 1.17E+00 | 2.78E−01 | 4.58E+00 | 1.98E+01 | 1.71E+00 | 6.10E−01 | 4.06E+01 | 7.94E+00 |
| LPsJ0209 | 1.50E+00 | 4.66E−01 | 3.73E+01 | 3.46E+01 | 1.12E+00 | 8.11E−02 | 3.88E+01 | 1.81E+00 |
| LPsJ0226 | 1.79E+00 | 6.31E−01 | 2.38E+00 | 1.24E+01 | 5.29E+00 | 1.24E+00 | 5.55E+01 | 7.10E+00 |
| LPsJ0305 | 1.09E+00 | 2.01E−01 | 2.85E+00 | 1.40E+01 | 1.98E+00 | 8.94E−01 | 6.63E+01 | 5.02E+01 |
| LPsJ0748 | 1.30E+00 | 3.63E−01 | 3.80E+00 | 1.98E+01 | 1.63E+00 | 4.99E−01 | 4.66E+01 | 6.39E+00 |
| LPsJ0846 | 1.06E+00 | 1.56E−01 | 8.70E−01 | 6.56E+00 | 2.04E+00 | 5.53E−01 | 5.22E+01 | 4.12E+00 |
| LPsJ105322 | 1.17E+00 | 2.25E−01 | 1.39E+01 | 1.30E+01 | 1.14E+00 | 1.14E−01 | 3.99E+01 | 1.79E+00 |
| LPsJ105353 | 1.13E+00 | 2.42E−01 | 2.89E+00 | 4.41E+00 | 2.99E+00 | 1.22E+00 | 4.63E+01 | 3.09E+00 |
| LPsJ112714 | 1.47E+00 | 5.61E−01 | 2.99E+00 | 1.37E+01 | 2.31E+00 | 1.17E+00 | 2.82E+01 | 6.39E+00 |
| LPsJ112713 | 1.93E+00 | 5.11E−01 | 7.61E−01 | 2.83E+00 | 3.26E+00 | 1.19E+00 | 4.35E+01 | 1.99E+00 |
| LPsJ1138 | 2.26E+00 | 4.96E−01 | 3.04E+00 | 1.19E+01 | 5.04E+00 | 1.16E+00 | 5.93E+01 | 1.12E+01 |
| LPsJ1139 | 1.14E+00 | 1.92E−01 | 1.91E+00 | 2.61E+00 | 1.29E+00 | 2.67E−01 | 3.90E+01 | 2.13E+00 |
| LPsJ1202 | 1.09E+00 | 1.91E−01 | 7.50E−01 | 2.35E+00 | 2.43E+00 | 6.47E−01 | 3.72E+01 | 1.64E+00 |
| LPsJ1322 | 2.08E+00 | 5.49E−01 | 1.90E+00 | 1.21E+01 | 3.06E+00 | 1.24E+00 | 5.17E+01 | 7.26E+00 |
| LPsJ1323 | 1.13E+00 | 2.24E−01 | 5.16E−01 | 3.26E+00 | 3.95E+00 | 1.17E+00 | 4.19E+01 | 2.44E+00 |
| LPsJ1326 | 1.53E+00 | 4.17E−01 | 6.35E−01 | 2.12E+00 | 2.45E+00 | 6.51E−01 | 3.72E+01 | 1.39E+00 |
| LPsJ1329 | 2.12E+00 | 6.51E−01 | 8.67E+00 | 1.16E+01 | 3.98E+00 | 1.09E+00 | 6.15E+01 | 1.26E+01 |
| LPsJ1336 | 1.23E+00 | 3.28E−01 | 1.29E+00 | 7.74E+00 | 4.14E+00 | 1.36E+00 | 5.01E+01 | 4.85E+00 |
| LPsJ1428 | 1.50E+00 | 5.69E−01 | 1.49E+01 | 2.10E+01 | 1.12E+00 | 3.77E−01 | 4.30E+01 | 2.12E+00 |
| LPsJ1449 | 1.13E+00 | 2.53E−01 | 5.92E+00 | 1.40E+01 | 1.27E+00 | 5.69E−01 | 5.18E+01 | 8.01E+00 |
| LPsJ1544 | 1.13E+00 | 2.02E−01 | 4.40E−01 | 1.07E+00 | 1.36E+00 | 2.19E−01 | 3.07E+01 | 6.69E−01 |
| LPsJ1607 | 1.53E+00 | 6.26E−01 | 1.60E+01 | 2.75E+01 | 1.52E+00 | 5.16E−01 | 3.41E+01 | 2.45E+00 |
| LPsJ1609 | 1.60E+00 | 3.26E−01 | 7.10E−01 | 1.50E+00 | 4.52E+00 | 1.17E+00 | 4.12E+01 | 1.41E+00 |
| LPsJ2313 | 1.62E+00 | 5.07E−01 | 1.34E+01 | 3.65E+01 | 2.42E+00 | 1.00E+00 | 3.54E+01 | 9.16E+00 |
| Sourctte ID | CO/H2 | Err, CO/H2 | [CI]/H2 | Err, [CI]/H2 | μLMISM | Err. μLMISM | LFIR | Err, LFIR |
|---|---|---|---|---|---|---|---|---|
| (—) | (—) | (—) | (—) | (—) | (M⊙) | (M⊙) | (L⊙) | (L⊙) |
| LPsJ0116 | 1.34E−04 | 2.82E−05 | 5.46E−05 | 2.52E−05 | 4.73E+12 | 5.47E+12 | 9.23E+13 | 9.42E+13 |
| LPsJ0209 | 1.23E−04 | 2.42E−05 | 3.04E−05 | 2.68E−05 | 6.51E+12 | 5.49E+11 | 1.33E+14 | 4.30E+12 |
| LPsJ0226 | 1.27E−04 | 2.77E−05 | 5.00E−05 | 5.00E−05 | 2.27E+12 | 2.80E+12 | 4.66E+14 | 1.04E+14 |
| LPsJ0305 | 1.18E−04 | 1.85E−05 | 6.06E−05 | 1.94E−05 | 1.45E+12 | 3.46E+11 | 1.68E+14 | 6.43E+13 |
| LPsJ0748 | 1.44E−04 | 2.81E−05 | 8.29E−05 | 2.63E−05 | 2.94E+12 | 4.00E+12 | 2.30E+14 | 6.12E+13 |
| LPsJ0846 | 1.24E−04 | 1.59E−05 | 1.05E−04 | 1.99E−05 | 2.12E+12 | 1.71E+12 | 3.52E+14 | 5.80E+13 |
| LPsJ105322 | 1.40E−04 | 3.02E−05 | 2.30E−05 | 9.86E−06 | 1.55E+13 | 3.60E+12 | 1.83E+14 | 4.56E+12 |
| LPsJ105353 | 1.15E−04 | 1.86E−05 | 3.74E−05 | 1.36E−05 | 2.41E+12 | 2.30E+11 | 2.33E+14 | 1.14E+13 |
| LPsJ112714 | 1.38E−04 | 2.93E−05 | 3.86E−05 | 2.18E−05 | 1.25E+12 | 1.32E+12 | 5.62E+12 | 2.47E+12 |
| LPsJ112713 | 1.45E−04 | 2.82E−05 | 1.05E−04 | 1.91E−05 | 1.10E+12 | 1.21E+11 | 1.05E+14 | 8.38E+12 |
| LPsJ1138 | 1.68E−04 | 2.64E−05 | 9.00E−05 | 2.57E−05 | 3.63E+11 | 3.77E+11 | 7.00E+13 | 3.77E+13 |
| LPsJ1139 | 1.17E−04 | 1.94E−05 | 3.69E−05 | 1.57E−05 | 3.11E+12 | 5.44E+11 | 6.32E+13 | 2.77E+12 |
| LPsJ1202 | 1.17E−04 | 1.97E−05 | 3.71E−05 | 1.52E−05 | 2.76E+12 | 2.74E+11 | 8.11E+13 | 4.03E+12 |
| LPsJ1322 | 1.50E−04 | 2.40E−05 | 1.22E−04 | 2.71E−05 | 5.04E+11 | 9.59E+11 | 9.99E+13 | 2.72E+13 |
| LPsJ1323 | 1.24E−04 | 2.34E−05 | 9.46E−05 | 1.48E−05 | 1.36E+12 | 1.55E+11 | 9.32E+13 | 6.26E+12 |
| LPsJ1326 | 1.37E−04 | 2.69E−05 | 1.11E−04 | 2.02E−05 | 1.40E+12 | 1.97E+11 | 4.61E+13 | 2.40E+12 |
| LPsJ1329 | 1.45E−04 | 3.27E−05 | 6.44E−05 | 2.22E−05 | 1.62E+12 | 4.78E+11 | 3.90E+14 | 1.64E+14 |
| LPsJ1336 | 1.36E−04 | 2.92E−05 | 8.83E−05 | 2.12E−05 | 1.79E+12 | 5.38E+11 | 1.77E+14 | 3.00E+13 |
| LPsJ1428 | 1.32E−04 | 2.55E−05 | 5.00E−05 | 5.00E−05 | 6.24E+11 | 8.04E+10 | 1.83E+13 | 1.09E+12 |
| LPsJ1449 | 1.19E−04 | 2.02E−05 | 3.61E−05 | 1.68E−05 | 1.52E+12 | 1.14E+12 | 1.17E+14 | 3.25E+13 |
| LPsJ1544 | 1.19E−04 | 2.03E−05 | 6.23E−05 | 1.91E−05 | 3.26E+12 | 3.32E+11 | 3.57E+13 | 6.12E+11 |
| LPsJ1607 | 1.30E−04 | 2.49E−05 | 5.00E−05 | 5.00E−05 | 5.89E+11 | 9.51E+10 | 7.78E+12 | 9.10E+11 |
| LPsJ1609 | 1.47E−04 | 2.77E−05 | 1.07E−04 | 2.02E−05 | 2.23E+12 | 2.09E+11 | 1.56E+14 | 6.78E+12 |
| LPsJ2313 | 1.46E−04 | 2.89E−05 | 1.00E−04 | 4.18E−05 | 2.99E+12 | 5.24E+12 | 4.11E+13 | 1.54E+13 |
Note. Individual χ2 weighted mean and standard deviation of the Turbulence model calculations of ∼2 million model. The FIR luminosity is calculated by integrating the dust SED between 40 and 120 μm.
Only a portion of this table is shown here to demonstrate its form and content. A machine-readable version of the full table is available.
Tables 11 and 12 present additional model fits for the best-fit 2-component models for each of the LPs.
Table 11. Best-fit Parameter Values for the 2-component Model
| ID | Comp | lognH2 | e_lognH2 | Tk | e_Tk | Radius | e_Radius | dv/dr | e_dv/dr | deltaV | e_deltaV | Tk/Td | e_Tk/Td |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (cm−3) | (cm−3) | K | K | pc | pc | km s−1 | km s−1 | km s−1 | km s−1 | ||||
| LPsJ0116 | COMP1 | 3.33 | 0.138 | 27.6 | 2.18 | 11300.0 | 1630.0 | 2.13 | 0.91 | 154.0 | 27.1 | 1.0 | 0.0827 |
| LPsJ0116 | COMP2 | 3.78 | 0.181 | 135.0 | 31.3 | 3160.0 | 1150.0 | 5.11 | 1.77 | 121.0 | 51.5 | 3.06 | 0.918 |
| LPsJ0209 | COMP1 | 3.47 | 0.00878 | 79.6 | 3.42 | 4590.0 | 47.5 | 4.26 | 0.0849 | 179.0 | 1.33 | 2.63 | 0.0238 |
| LPsJ0209 | COMP2 | 5.88 | 0.0937 | 97.7 | 0.761 | 2500.0 | 19.7 | 32.6 | 4.58 | 49.3 | 3.05 | 1.14 | 0.0311 |
Note. The best-fit, minimum-χ2 model parameters (see Table 3) for each galaxy based on the 2-component model.
Only a portion of this table is shown here to demonstrate its form and content. A machine-readable version of the full table is available.
Download table as: DataTypeset image
Table 12. Derived Quantities Based on the Values in Table 11
| ID | Component | LFIR | e_LFIR | Td | e_Td | lambda0 | e_lambda0 | NH2 | e_NH2 |
|---|---|---|---|---|---|---|---|---|---|
| (Lsun) | (Lsun) | (K) | (K) | (μm) | (μm) | (cm−2) | (cm−2) | ||
| LPsJ0116 | COMP1 | 4.67E+13 | 1.24E+13 | 27.6 | 1.33 | 89.0 | 22.25 | 5.47e+23 | 1.3675e+23 |
| LPsJ0116 | COMP2 | 4.54E+13 | 4.22E+13 | 46.1 | 9.51 | 76.8 | 19.2 | 4.08e+23 | 1.02e+23 |
| LPsJ0209 | COMP1 | 1.39E+13 | 4.14E+12 | 30.3 | 1.58 | 76.0 | 19.0 | 3.83e+23 | 9.575e+22 |
| LPsJ0209 | COMP2 | 2.58E+14 | 5.13E+12 | 85.7 | 1.74 | 227.0 | 56.75 | 3.42e+24 | 8.55e+23 |
Note. These quantities are derived using the best-fit, minimum-χ2 model parameters for each galaxy based on the 2-component model.
Only a portion of this table is shown here to demonstrate its form and content. A machine-readable version of the full table is available.
Download table as: DataTypeset image
Footnotes
- 23
H2 is a low-mass quantum rotor with the first quadrupole transition,
 0 at 28 μm, requires hν/kB ∼ 500 K to excite the lowest transition (Dabrowski 1984).
0 at 28 μm, requires hν/kB ∼ 500 K to excite the lowest transition (Dabrowski 1984). - 24
We have used astropy.cosmology (Astropy Collaboration et al. 2018).
- 25
Software information can be found at http://www.iram.fr/IRAMFR/GILDAS.
- 26
- 27
Asymmetric lines could also indicate viewing a galactic system at a specific edge on orientation that covers an asymmetric portion of a rotating spheroidal disk or a significantly turbulent environment (e.g., Puschnig et al. 2020).
- 28
λ0 is directly proportional to the dust column density.
- 29
 is subject to large uncertainties in dust grain size distributions (Draine 2011).
is subject to large uncertainties in dust grain size distributions (Draine 2011). - 30
This is comparable to setting an upper limit for the dust temperature.
- 31
A p-value of 0.05 or less allows one to reject the null hypothesis that the two samples of kinetic temperatures come from the same distribution.
- 32
We note that the values of λ0 for each component are in agreement for the LPs for which we have applied a dust SED prior (see Section 5.2).
- 33
Corrected by the helium abundance, a factor of 1.36 (Allen 1973).
- 34
Note that we have used a fiducial value of R2,1 = 0.75 to make this comparison, since only CO (2−1) line measurements are available.
- 35
Also referred to as the Red Radio Ring.
- 36
Also referred to as PLCK G244.8+54.9.
- 37
Without further information on the FIR fine-structure lines for the sample of LPs, we are unable to make a full comparison using the CO cooling budget alone.
- 38
Note that Rosenberg et al. (2014) scale this simple mechanical heating term between normalized values of 0 and 1 and combine this with their PDR model in order to match the LVG derived values of the Tkin.
- 39
- 40
Due to, e.g., Rayleigh–Taylor instabilities.
- 41
- 42
This is in addition to the turbulent motions generated from hydrodynamic gas motions causing gravitational shear forces.
















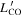
![${L}_{[{\rm{C}}\,{\rm\small{I}}]}^{{\prime} }$](https://content.cld.iop.org/journals/0004-637X/908/1/95/revision1/apjabcc01ieqn107.gif)






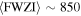
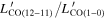

![$\langle [[{\rm{C}}\,{\rm\small{I}}]]/[{{\rm{H}}}_{2}]\rangle \,\sim 6.8\times {10}^{-5}$](https://content.cld.iop.org/journals/0004-637X/908/1/95/revision1/apjabcc01ieqn154.gif)