Hostname: page-component-76fb5796d-vfjqv Total loading time: 0 Render date: 2024-04-26T06:39:23.025Z Has data issue: false hasContentIssue false
  • English
  • Français

Powers of Principal Q-Borel ideals

Part of: Algebraic combinatorics

Published online by Cambridge University Press:  23 August 2021

Eduardo Camps-Moreno ,
Craig Kohne ,
Eliseo Sarmiento  and
Adam Van Tuyl
Eduardo Camps-Moreno*
Affiliation:
Escuela Superior de Física y Matemáticas, Mexico City, Mexico
Craig Kohne
Affiliation:
McMaster University, Hamilton, ON, Canada e-mail: kohnec@math.mcmaster.ca
Eliseo Sarmiento
Affiliation:
Escuela Superior de Física y Matemáticas, Mexico City, Mexico e-mail: esarmiento@ipn.mx
Adam Van Tuyl
Affiliation:
McMaster University, Hamilton, ON, Canada e-mail: vantuyl@math.mcmaster.ca
*
e-mail: camps@esfm.ipn.mx
Get access Rights & Permissions [Opens in a new window]

Abstract

Fix a poset Q on $\{x_1,\ldots ,x_n\}$ . A Q-Borel monomial ideal 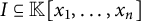$I \subseteq \mathbb {K}[x_1,\ldots ,x_n]$ is a monomial ideal whose monomials are closed under the Borel-like moves induced by Q. A monomial ideal I is a principal Q-Borel ideal, denoted $I=Q(m)$ , if there is a monomial m such that all the minimal generators of I can be obtained via Q-Borel moves from m. In this paper we study powers of principal Q-Borel ideals. Among our results, we show that all powers of 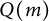$Q(m)$ agree with their symbolic powers, and that the ideal 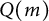$Q(m)$ satisfies the persistence property for associated primes. We also compute the analytic spread of 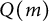$Q(m)$ in terms of the poset Q.

Keywords

monomial idealsQ-Borelsymbolic powersanalytic spreadpersistence of primes

MSC classification

Primary: 05E40: Combinatorial aspects of commutative algebra
Type
Article
Information
Canadian Mathematical Bulletin , Volume 65 , Issue 3 , September 2022 , pp. 633 - 652
Check for updates
Copyright
© Canadian Mathematical Society 2021

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Camps is supported by Conacyt. Sarmiento’s research is supported by SNI-Conacyt. Camps and Sarmiento are supported by PIFI IPN 20201016. Van Tuyl’s research is supported by NSERC Discovery Grant 2019-05412.

References

Bhat, A., Associated primes and Betti splitting of some generalized Borel ideals. Ph.D. thesis, Oklahoma State University, 2019.Google Scholar
Bocci, C., Cooper, S., Guardo, E., Harbourne, B., Janssen, M., Nagel, U., Seceleanu, A., Van Tuyl, A., and The, T. V., Waldschmidt constant for squarefree monomial ideals . J. Algebraic Combin. 44(2016), no. 4, 875–904.CrossRefGoogle Scholar
Bocci, C. and Harbourne, B., Comparing powers and symbolic powers of ideals . J. Algebraic Geom. 19(2010), no. 3, 399–417.10.1090/S1056-3911-09-00530-XCrossRefGoogle Scholar
Camps-Moreno, E., Kohne, C., Sarmiento, E., and Van Tuyl, A., On the Waldschmidt constant of square-free principal Borel ideals. Preprint, 2021. arXiv:2105.07307.10.1090/proc/16082CrossRefGoogle Scholar
Carlini, E., Hà, H. T., Harbourne, B., and Van Tuyl, A., Ideals of powers and powers of ideals: intersecting algebra, geometry, and combinatorics, Lecture Notes of the Unione Matematica Italiana, 27, Springer: Cham, Switzerland, 2020.CrossRefGoogle Scholar
Conca, A. and Herzog, J., Castelnuovo–Mumford regularity of products of ideals . Collect. Math. 54(2003), no. 2, 137–152.Google Scholar
Conca, A. and Tsakiris, M. C., Resolution of ideals associated to subspace arrangements. Preprint, 2020. arXiv:1910.01955.Google Scholar
Cooper, S. M., Embree, R. J., Hà, H. T., and Hoefel, A. H., Symbolic powers of monomial ideals . Proc. Edinb. Math. Soc. (2) 60(2017), no. 1, 39–55.CrossRefGoogle Scholar
Dao, H., De Stefani, A., Grifo, E., Huneke, C., and Núñez-Betancourt, L., Symbolic powers of ideals . In: Singularities and foliations. Geometry, topology and applications, Proceedings in Mathematics & Statistics 222 (eds Araujo dos Santos, R. N., Menegon Neto, A., Mond, D., Saia, M. J. and Snoussi, J.), Springer: Cham, Switzerland, 2018, pp. 387–432.CrossRefGoogle Scholar
Ein, L., Lazarsfeld, R., and Smith, K., Uniform behavior of symbolic powers of ideals . Invent. Math. 144(2001), no. 2, 241–252.10.1007/s002220100121CrossRefGoogle Scholar
Francisco, C. A., Mermin, J., and Schweig, J., Borel generators . J. Algebra 332(2011), no. 1, 522–542.CrossRefGoogle Scholar
Francisco, C. A., Mermin, J., and Schweig, J., Generalizing the Borel property . J. Lond. Math. Soc. 87(2013), no. 3, 724–740.10.1112/jlms/jds071CrossRefGoogle Scholar
Galetto, F., Geramita, A. V., Shin, Y.-S., and Van Tuyl, A., The symbolic defect of an ideal . J. Pure Appl. Algebra 223(2019), no. 6, 2709–2731.10.1016/j.jpaa.2018.11.019CrossRefGoogle Scholar
Godsil, C. and Royle, G. F., Algebraic graph theory, Graduate Texts in Mathematics, 207, Springer-Verlag, New York, 2013.Google Scholar
Herzog, J., Generic initial ideals and graded Betti numbers . In: Computational commutative algebra and combinatorics, (ed. Hibi, T.) Mathematical Society of Japan, Tokyo, 2002, pp. 75–120.CrossRefGoogle Scholar
Herzog, J. and Qureshi, A. A., Persistence and stability properties of powers of ideals . J. Pure Appl. Algebra 219(2015), no. 3, 530–542.10.1016/j.jpaa.2014.05.011CrossRefGoogle Scholar
Herzog, J., Rauf, A., and Vladoiu, M., The stable set of associated prime ideals of a polymatroidal ideal . J. Algebraic Combin. 37(2013), no. 2, 289–312.CrossRefGoogle Scholar
Hochster, M. and Huneke, C., Comparison of symbolic and ordinary powers of ideals . Invent. Math. 147(2002), no. 2, 349–369.CrossRefGoogle Scholar
Huneke, C. and Swanson, I., Integral closure of ideals, rings, and modules. Vol. 13, Cambridge University Press, Cambridge, 2006.Google Scholar
Martínez-Bernal, J., Morey, S., and Villarreal, R. H., Associated primes of powers of edge ideals . Collect. Math. 63(2012), no. 3, 361–374.10.1007/s13348-011-0045-9CrossRefGoogle Scholar
Villarreal, R., Monomial algebras. 2nd ed., CRC Press, New York, 2015.Google Scholar