Two binary structures \(\mathfrak{R}\) and \(\mathfrak{R’}\) on the same vertex set \(V\) are \((\leq k)\)-hypomorphic for a positive integer \(k\) if, for every set \(K\) of at most \(k\) vertices, the two binary structures induced by \(\mathfrak{R}\) and \(\mathfrak{R’}\) on \(K\) are isomorphic. A binary structure \(\mathfrak{R}\) is \((\leq k)\)-reconstructible if every binary
structure \(\mathfrak{R’}\) that is \((\leq k)\)-hypomorphic to \(\mathfrak{R}\) is isomorphic to \(\mathfrak{R}\). In this paper, we describe the pairs of \((\leq 3)\)-hypomorphic posets and the pairs of \((\leq 3)\)-hypomorphic bichains. As a consequence, we characterize the \((\leq 3)\)-reconstructible posets and the \((\leq 3)\)-reconstructible bichains. This answers a question suggested by Y. Boudabbous and C. Delhommé during a personal communication.
All binary relations considered in this paper are irreflexive binary relations. Two binary relations \(\mathcal{R}_1\) and \(\mathcal{R}_2\) on the same vertex set \(V\) are \((\leq k)\)-hypomorphic for a positive integer \(k\) if, for every set \(K\) of at most \(k\) vertices, the two binary relations induced by \(\mathcal{R}_1\) and \(\mathcal{R}_2\) on \(K\) are isomorphic. A binary relation \(\mathcal{R}\) is \((\leq k)\)-reconstructible if every binary relation \(\mathcal{R'}\) that is \((\leq k)\)-hypomorphic to \(\mathcal{R}\) is isomorphic to \(\mathcal{R}\). G. Lopez showed in [1, 2, 3] that finite binary relations are \((\leq 6)\)-reconstructible. This work was extended to the infinite case by J.G. Hagendorf in [4]. These works make essential use of difference classes introduced by Lopez [2, 3]. Based on the description by Lopez and C. Rauzy [5] of the difference classes of finite \((\leq4)\)-hypomorphic binary relations, Y. Boudabbous [6] provided a characterization of the \((\leq 5)\)-reconstructible finite binary relations, that generalizes to \((\leq 4)\)-reconstructibility. On the other hand, in [7] Boudabbous and C. Delhommé characterized the \((\leq k)\)-reconstructible binary relations (finite or not), for each \(k\geq 4\). For the \((\leq3)\)-reconstruction, Boudabbous and Lopez [8] characterized the finite binary relations that are \((\leq 3)\)-reconstructible. Hagendorf [4] proved that every finite poset with at least \(4\) vertices is \((\leq 3)\)-reconstructible. In [9] Boudabbous and Delhommé suggested the question about the characterization of the \((\leq 3)\)-reconstruction of posets and bichains. In this paper, we give an answer to this question as follows. We first describe the pairs of \((\leq 3)\)-hypomorphic posets and the pairs of \((\leq 3)\)-hypomorphic bichains. As a consequence of these descriptions, we give a characterization of the \((\leq 3)\)-reconstructible posets and bichains:
Theorem 1. Two posets are \((\leq 3)\)-hypomorphic if and only if they have the same maximal chain-modules, and they have the same corresponding quotient relation.
Theorem 2. Two bichains are \((\leq3)\)-hypomorphic if and only if they have the same partition into maximal linear-modules, the two corresponding quotients are equal, and each maximal linear-module has the same kind in both.
We deduce the following \((\leq 3)\)-reconstruction results.
Corollary 1. A poset is \((\leq 3)\)-reconstructible if and only if its chain-modules are finite.
Corollary 2. A bichain is \((\leq 3)\)-reconstructible if and only if its linear-modules are finite.
A binary structure is a pair \(\mathfrak{R} := (V,(\mathcal{R}_i )_{i\in I})\) made of a set \(V\) and a family \((\mathcal{R}_i )_{i\in I}\) of binary relations on \(V\). When \(|I|=1\), the binary structure is a binary relation. A binary relation \((V,\mathcal{R})\) is a partially ordered set (order or poset) if the relation \(\mathcal{R}\) is an irreflexive, antisymmetric and transitive binary relation on \(V\). The binary structure is a bichain when \(|I|=2\) and \(\mathcal{R}_1\) and \(\mathcal{R}_2\) are linear orderings (or simply chains). The substructure induced by \(\mathfrak{R}\) on a subset \(A\) of \(V\), simply called the restriction of \(\mathfrak{R}\) to \(A\), is the binary structure \(\mathfrak{R}\upharpoonright A:= (A, (\mathcal{R}_i\upharpoonright A)_{i\in I} )\), where \(\mathcal{R}_i\upharpoonright A:= \mathcal{R}_i\cap A^{2}\) for all \(i\in I\). Finally, a set \(M\) of vertices is a module [10, 11] (is an interval [12], is an autonomous set [13] or a clan [14] ) of \(\mathfrak{R}\), if for each \(i\in I\),
(\((b,a)\in \mathcal{R}_i \Longleftrightarrow (b,a')\in \mathcal{R}_i\)) and (\((a,b)\in \mathcal{R}_i \Longleftrightarrow (a',b)\in \mathcal{R}_i\)) for any vertices \(a,a',b\) with \(a,a'\in M\) and \(b\notin M\).
The empty set, the singletons of \(V\) and the set \(V\) are modules of \(\mathfrak{R}\) and said to be trivial. Notice for instance that if the two linear orderings of a bichain have a common extremum \(x\) (that may be a minimum for one and a maximum for the other one), then \(V\setminus \{x\}\) is a module of the bichain.
The following is easy to check;
Lemma 1. The collection \(\mathcal{M}\) of modules of a binary structure \(\mathfrak{R}\) with vertex set \(V\) satisfies the following properties;
It contains the empty set, the singletons and the vertex set (trivial modules).
It is closed under arbitrary intersection, i.e. \(\forall \mathcal{N}\subseteq \mathcal{M }\): \(\cap \mathcal{N }\in \mathcal{M}\)(with the convention that \(\cap \varnothing = V\)).
It contains the union of any subcollection with a non-empty intersection, i.e. \(\forall \mathcal{N }\subseteq \mathcal{M}(\cap \mathcal{N}\neq \varnothing\Rightarrow \cup \mathcal{N }\in \mathcal{M})\).
It is closed under balanced difference, i.e. \(\forall M, N\in \mathcal{M}\)(\(M\setminus N\neq \varnothing \Rightarrow N\setminus M\in \mathcal{M}\)).
A modular partition of a binary structure \(\mathfrak{R}\) is a partition \(\mathcal{P}\) of its vertex set \(V\) into modules of \(\mathfrak{R}\). Notice that the elements of
such a partition are non-empty. The elements of \(\mathcal{P}\) may be considered as the
vertices of a new binary structure, the quotient \(\mathfrak{R}/\mathcal{P}\) of \(\mathfrak{R}\) by \(\mathcal{P}\), defined as follows:
\(\mathfrak{R}/\mathcal{P}:=(\mathcal{P},(\mathcal{R}_{i}/\mathcal{P})_{i\in
I})\), where for all \(i\in I\),
\(\mathcal{R}_{i}/\mathcal{P}\) is a
binary relation defined on \(\mathcal{P}\) by: \[For~all~ A\neq B\in \mathcal{P}, (A,B)\in
\mathcal{R}_{i}/\mathcal{P}\Leftrightarrow
(a,b)\in \mathcal{R}_{i},~for~any~vertices~a,b~with~ a\in A~and~ b\in
B.\]
Let \(\mathfrak{R} := (V, (\mathcal{R}_i )_{i\in I})\) and \(\mathfrak{R}' := (V', (\mathcal{R}'_i )_{i\in I})\) be two binary structures. A map \(f : V \longrightarrow V'\) is an isomorphism from \(\mathfrak{R}\) onto \(\mathfrak{R}'\) if \(f\) is bijective and satisfies: \((x, y )\in \mathcal{R}_i\) if and only if \(( f (x), f (y))\in \mathcal{R}'_i\), for any \((x, y )\in V^{2}\), \(i\in I\). The binary structure \(\mathfrak{R}\) is isomorphic to \(\mathfrak{R}'\) if there is some isomorphism from \(\mathfrak{R}\) onto \(\mathfrak{R}'\), which is denoted \(\mathfrak{R}\simeq \mathfrak{R}'\). The binary structure \(\mathfrak{R}\) is embeddable into \(\mathfrak{R}'\), which is denoted \(\mathfrak{R}\leq \mathfrak{R}'\), if \(\mathfrak{R}\) is isomorphic to some restriction of \(\mathfrak{R}'\).
We recall the basic notions of the reconstruction problems in the theory of relations that we apply to the case of binary structures. Let \(\mathfrak{R}\) and \(\mathfrak{R}'\) be two binary structures on the same set \(V\) and let \(k\) be a positive integer. The binary structure \(\mathfrak{R}'\) is \((\leq k)\)–hypomorphic to \(\mathfrak{R}\) if for each subset \(A\) of \(V\) with at most \(k\) elements, the induced binary structures \(\mathfrak{R}'\upharpoonright A\) and \(\mathfrak{R}\upharpoonright A\) are isomorphic. The binary structure \(\mathfrak{R}\) is \((\leq k)\)–reconstructible, if each binary structure \((\leq k)\)-hypomorphic to \(\mathfrak{R}\) is isomorphic to \(\mathfrak{R}\).
Lemma 2. Consider two binary structures \(\mathfrak{R}\) and \(\mathfrak{R'}\) with the same vertex set and a common modular partition \(\mathcal{M}\) such that \(\mathfrak{R}/ \mathcal{M}= \mathfrak{R}'/ \mathcal{M}\). Then the following assertions hold.
If the restrictions \(\mathfrak{R}\upharpoonright M\) and \(\mathfrak{R}'\upharpoonright M\) are isomorphic for each member \(M\) of \(\mathcal{M}\), then \(\mathfrak{R}\) and \(\mathfrak{R}'\) are isomorphic.
For \(k\geq 1\), if \(\mathfrak{R}\upharpoonright M\) and \(\mathfrak{R}'\upharpoonright M\) are \((\leq k)\)-hypomorphic for each \(M\in \mathcal{M}\), then \(\mathfrak{R}\) and \(\mathfrak{R}'\) are \((\leq k)\)-hypomorphic.
Proof. Clearly, the first assertion is easy to check. Now, consider an integer \(k\geq 1\) and let us prove the second assertion. Consider two binary structures \(\mathfrak{R}\) and \(\mathfrak{R'}\) with the same vertex set \(V\) and a common modular partition \(\mathcal{M}\) such that \(\mathfrak{R}/ \mathcal{M}= \mathfrak{R}'/ \mathcal{M}\), and \(\mathfrak{R}\upharpoonright M\) and \(\mathfrak{R}'\upharpoonright M\) are \((\leq k)\)-hypomorphic for each \(M\in \mathcal{M}\). Given a subset \(X\) of \(V\) with \(|X|\leq k\), we will show that \(\mathfrak{R}\upharpoonright X\simeq \mathfrak{R'}\upharpoonright X\). Let \(X_{\mathcal{M}}\) denote the set \(\{Y\cap X: Y\in\mathcal{M}\ and\ Y\cap X\neq \emptyset \}\). Since \(\mathcal{M}\) is a common modular partition of \(\mathfrak{R}\) and \(\mathfrak{R'}\) and \(\mathfrak{R}/\mathcal{M}=\mathfrak{R'}/\mathcal{M}\), \(X_{\mathcal{M}}\) is a common modular partition of \(\mathfrak{R}\upharpoonright X\) and \(\mathfrak{R'}\upharpoonright X\), and \((\mathfrak{R}\upharpoonright X)/X_{\mathcal{M}}= (\mathfrak{R'}\upharpoonright X)/X_{\mathcal{M}}\). Since \(\mathfrak{R}\upharpoonright M\) and \(\mathfrak{R}'\upharpoonright M\) are \((\leq k)\)-hypomorphic for each \(M\in \mathcal{M}\), \((\mathfrak{R}\upharpoonright X)\upharpoonright Y\simeq (\mathfrak{R'}\upharpoonright X)\upharpoonright Y\), for each element \(Y\) of \(X_{\mathcal{M}}\). If \(X_{\mathcal{M}}\) is a singleton \(\{Y \}\), then \(\mathfrak{R}\upharpoonright X \simeq \mathfrak{R'}\upharpoonright X\) because \(\mathfrak{R}\upharpoonright X = (\mathfrak{R}\upharpoonright X)\upharpoonright Y\) and \(\mathfrak{R'}\upharpoonright X = (\mathfrak{R'}\upharpoonright X)\upharpoonright Y\). Otherwise, by the first assertion applied to \(\mathfrak{R}\upharpoonright X\) and \(\mathfrak{R'}\upharpoonright X\), \(\mathfrak{R}\upharpoonright X\simeq \mathfrak{R'}\upharpoonright X\). Thus, \(\mathfrak{R}\) and \(\mathfrak{R'}\) are \((\leq k)\)-hypomorphic. ◻
Let \(P:=(V,\mathcal{R})\) be a poset. By \(x <_P y\), we denote the fact that \((x, y) \in \mathcal{R}\). By \(x \parallel_P y\), we denote the fact that \((x, y) \notin \mathcal{R}\) and \((y,x) \notin \mathcal{R}\). The dual of \(P\) is the poset denoted by \(P^*\) and defined on the set \(V\) as follows: \(x <_{P^*} y\) if and only if \(y <_P x\). Finally, remark that \(P\) and \(P^*\) have the same modules.
Notation 1. Given a poset \(P\) on a vertex set \(V\), let \(A\) and \(B\) be two disjoint subsets of \(V\), and \(x\) be an element of \(V\setminus A\). Write,
\(A<_P B\), if \(a<_P b\) for all \(a\in A\) and for all \(b\in B\).
\(A\parallel_P B\), if \(a\parallel_P b\) for all \(a\in A\) and for all \(b\in B\).
For \(A=\{a\}\), \(A<_P B\) (respectively \(A\parallel_P B\)) will be denoted simply by
\(a<_P B\) (respectively \(a\parallel_P B\)).
For \(B=\{b\}\), \(A<_P B\) (respectively \(A\parallel_P B\)) will be denoted simply by
\(A<_P b\) (respectively \(A\parallel_P b\)).
\(x \thicksim_{P} A\) (or simply \(x \thicksim A\)), if \(A\) is a module of \(P\upharpoonright A\cup \{x\}\), i.e. \(x<_P A\) or \(A<_P x\) or \(x\parallel_P A\).
\(x \nsim_{P} A\) (or simply \(x \nsim A\)), if \(A\) is not a module of \(P\upharpoonright A\cup \{x\}\).
In this subsection, we present some useful particular posets.
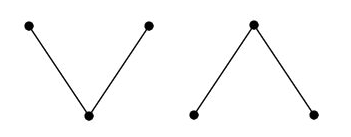
\(\mathcal{V}\)-order
A 3-element order is called \(\mathcal{V}\)-order if it is isomorphic to one of the two orders illustrated in Figure 1.
Lozenge
A 4-element order is called a lozenge if it is isomorphic to the order illustrated in Figure 2.

Chain-modules
A chain-module \(M\) of a poset \(P\) is a module of \(P\) which is a chain.
In [7], the authors showed that the maximal chain-modules form a partition of the vertex set of a given binary relation and they showed the following lemma.
Lemma 3. [7] Given a binary relation \(\mathcal{R}\), the union of any collection of chain-modules containing a given vertex is a chain-module. Every non-empty chain-module of \(\mathcal{R}\) is included in a unique maximal one. In particular, the maximal chain-modules form a partition of its vertex set, and in the corresponding quotient relation the chain-modules have at most one element.
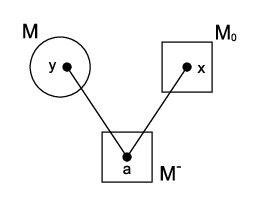
Notation 2. Given a poset \(P\) on a vertex set \(V\), and a proper module \(M\) of \(P\), we consider the following useful subsets of \(V\setminus M\);
\(M_{0}=\{a\in V \setminus M \ such\ that \ a \parallel_P M \}\).
\(M^{-}=\{a\in V \setminus M \ such \ that \ a <_P M \}\).
\(M^{+}=\{a\in V \setminus M \ such \ that \ M <_P a\}\).
Remark 1. The set of non-empty elements of \(\{M_{0},M^{+},M^{-}\}\) is a partition of \(V\setminus M\).
Proposition 1. Given a poset \(P\) on a vertex set \(V\) such that \(P\) is not a chain, consider a maximal chain-module \(M\) of \(P\) and an element \(a\) of \(M^{-}\) (respectively \(M^+\)). Then at least one of the assertions below holds;
There is \(x \in M_{0}\) such that \(P\upharpoonright \{a,x,y \}\) is a \(\mathcal{V}\)-order, for all \(y\in M\) (see Figure 3).
There is \(x\in M^{-} \setminus \{a\}\) (respectively \(M^{+} \setminus \{a\}\)) such that \(P \upharpoonright \{a,x,y \}\) is a \(\mathcal{V}\)-order, for all \(y\in M\) (see Figure 4).
There are \(x\neq y \in M^{-} \setminus \{a\}\) (respectively \(M^{+} \setminus \{a\}\)) such that \(P\upharpoonright \{a,x,y,z \}\) is a lozenge, for all \(z\in M\) (see Figure 5).


Proof. By Interchanging \(P\) and \(P^*\), we may assume that \(a\in M^-\). We distinguish the following
two cases according to the comparability of \(a\) and the elements of \(M_0\).
Case 1: There is \(x\in
M_0\) such that \(a\) and \(x\) are comparable. Since \(a <_P M\) and \(M \parallel_P x\), \(a <_P x\). Therefore, \(P\upharpoonright \{a,x,y \}\) is a \(\mathcal{V}\)-order, for all \(y\in M\), and thus assertion (1)
holds.
Case 2: For all \(z\in
M_0\), \(a\parallel_P z\); i.e.
\(a\parallel_P M_0\). Recall that \(M\cup \{x\}\) is a chain by the definition
of \(M^-\). Using the maximality of the
chain-module \(M\) in \(P\), we conclude that \(|M^-|\geq 2\). Now, according to the
comparability between \(a\) and the
elements of \(M^- \setminus \{a\}\), we
will discuss the following two subcases.
Case 2.1: There is \(x\in M^-
\setminus \{a\}\) such that \(x\parallel_P a\). In this case, \(P\upharpoonright \{a,x,y \}\) is a \(\mathcal{V}\)-order, for all \(y\in M\), and thus assertion (2)
holds.
Case 2.2: For all \(t\in M^-
\setminus \{a\}\), \(a\) and
\(t\) are comparable. Remark that \(M\cup \{a\}\cup (\{a\}^+\cap M^-) <_P
M^+\) (because \(M\cup M^-
<_P M^+\)) and \((\{a\}^-\cap M^-)
<_P M\cup \{a\}\cup (\{a\}^+\cap M^-)\). In addition, since
\(a<_P (\{a\}^+\cap M^-)\), \(a\parallel_P M_0\) and \(M \parallel_P M_0\), \((\{a\}^+\cap M^-) \parallel_P M_0\). Thus,
\(M\cup \{a\}\cup (\{a\}^+\cap M^-)
\parallel_P M_0\). It follows that, \(M\cup \{a\}\cup (\{a\}^+\cap M^-)\) is a
module of \(P\). Using the maximality
of \(M\) in \(P\), it follows that, \((\{a\}^+\cap M^-) \cup \{a\}\) is not a
chain of \(P\). Therefore, \(| (\{a\}^+\cap M^-)|\geq 2\), and there are
\(x\neq y\in (\{a\}^+\cap M^-)\) such
that \(x\parallel_P y\). Consequently,
\(P\upharpoonright \{a,x,y,z \}\) is a
lozenge for all \(z\in M\). Thus,
assertion (3) holds. ◻
Remark 2. By Proposition 1, each element of \(M^+\cup M^-\) belongs to a \(\mathcal{V}\)-order or a lozenge of \(P\).
The following useful remark is easily verified;
Remark 3. Consider two \((\leq 3)\)-hypomorphic posets \(P\) and \(P'\) on the same vertex set \(V\) and a subset \(X\) of \(V\). If \(P\upharpoonright X\) is a \(\mathcal{V}\)-order or a lozenge, then \(P'\upharpoonright X=P\upharpoonright X\).
Corollary 3. Given two \((\leq 3)\)-hypomorphic posets \(P\) and \(P'\) on the same vertex set \(V\), consider a maximal chain-module \(M\) of \(P\). Then \(P'\upharpoonright \{a,x\}=P\upharpoonright \{a,x\}\), for all \(x\in V\setminus M\) and \(a\in M\).
Proof. Since the result is clear if \(P\) is a chain, assume that \(M\neq V\), and consider an element \(x\) of \(V\setminus M\) and an element \(a\) of \(M\). By Remark 1, \(x\in M_0\cup M^- \cup M^+\). Without loss of generality, by interchanging \(P\) and \(P^*\), we may assume that \(x\) is an element of \(M_0\cup M^-\). First, assume that \(x\in M_0\). Then, \(P'\upharpoonright \{a,x\}=P\upharpoonright \{a,x\}\) because \(P\) and \(P'\) are \((\leq 2)\)-hypomorphic. Second, assume that \(x\in M^-\). By Remark 2, the vertex \(x\) belongs to a \(\mathcal{V}\)-order or a lozenge. In the first case, by Proposition 1, there is \(b\in M_0\cup M^-\) such that \(P\upharpoonright \{a,b,x\}\) is a \(\mathcal{V}\)-order of \(P\). Since the posets \(P\) and \(P'\) are \((\leq 3)\)-hypomorphic and \(P\upharpoonright \{a,b,x\}\) is a \(\mathcal{V}\)-order, \(P'\upharpoonright \{a,b,x\}=P\upharpoonright \{a,b,x\}\) by Remark 3. In particular, \(P'\upharpoonright \{a,x\}=P\upharpoonright \{a,x\}\). In the second case, by Proposition 1, there are \(b\neq c\in (M^-\setminus \{x\})\) such that \(P\upharpoonright \{a,b,c,x\}\) is a lozenge of \(P\). Since \(P\) and \(P'\) are \((\leq 3)\)-hypomorphic and \(P\upharpoonright \{a,b,c,x\}\) is a lozenge, by Remark 3, \(P'\upharpoonright \{a,b,c,x\}=P\upharpoonright \{a,b,c,x\}\). Consequently, \(P'\upharpoonright \{a,x\}=P\upharpoonright \{a,x\}\). ◻
Consider two \((\leq 3)\)-hypomorphic posets \(P\) and \(P^{'}\) with the same vertex set \(V\). By Lemma 3, the maximal chain-modules of \(P\) and those of \(P'\) form two partitions of \(V\). Denote by \(\mathcal{Q}\) and \(\mathcal{Q'}\) the partition of \(V\) in maximal chain-modules of \(P\) and \(P'\) respectively. Consider an element \(M\) of \(\mathcal{Q}\). Since \(P\) and \(P'\) are \((\leq 3)\)-hypomorphic, \(M\) is a chain of \(P'\). Now, consider an element \(x\) of \(V\setminus M\). By Corollary 3, \(P'\upharpoonright \{a,x\}= P\upharpoonright \{a,x\}\), for all \(a\in M\). Moreover, \(x \sim M\) in \(P\) because \(M\) is a module of \(P\). It follows that, \(x \sim M\) in \(P'\), and hence \(M\) is a chain-module of \(P'\). Let \(M'\) be the element of \(\mathcal{Q'}\) including \(M\). By what precedes, \(M'\) is a chain-module of \(P\). Thus, there is an element \(M''\) of \(\mathcal{Q}\) including \(M'\). Consequently, \(M''=M'=M\), and hence \(\mathcal{Q'}=\mathcal{Q}\). Finally, Corollary 3 implies that the quotient relations \(P/ \mathcal{Q}\) and \(P'/\mathcal{Q}\) are equal.
Conversely, consider two posets \(P\) and \(P'\) on the same vertex set \(V\) having the same modular partition \(\mathcal{Q}\) on maximal chain-modules such that \(P/\mathcal{Q} = P'/\mathcal{Q}\). We have to prove that \(P\) and \(P'\) are \((\leq 3)\)-hypomorphic. Let \(M\in \mathcal{Q}\). Since \(M\) is a chain of \(P\) and \(P'\), \(P\upharpoonright M\) and \(P'\upharpoonright M\) are \((\leq3)\)-hypomorphic. By Lemma 2, it follows that \(P\) and \(P'\) are \((\leq 3)\)-hypomorphic.
Remark 4. Theorem 1 can be obtained by the use of the difference classes introduced by G. Lopez [1, 2, 3], but our proof is self-contained.
Given a bichain \(\mathfrak{B}:=(V,L_1,L_2)\), a vertex subset \(W\) is called linear if \(L_{2}\upharpoonright W=L_{1}\upharpoonright W\) or \(L_{2}\upharpoonright W=L^*_{1}\upharpoonright W\). In the first case, \(W\) is positive linear and in the second it is negative linear. If in addition \(W\) is a module of \(\mathfrak{B}\), speak of linear-module, positive linear-module and negative linear-module. If \(L_2=L_1\) or \(L_2=L^*_1\), speak of linear-bichain, positive linear-bichain and negative linear-bichain. Finally, we say that two linear-bichains have the same kind if they are both positive or both negative.
We prove the following useful result by considering the linear-modules of a given bichain.
Lemma 4. Given a bichain \(\mathfrak{B}\), the union of any collection of linear-modules containing a given vertex is a linear-module. Every non-empty linear-module of \(\mathfrak{B}\) is included in a unique maximal one. In particular, the maximal linear-modules of \(\mathfrak{B}\) form a modular partition of \(\mathfrak{B}\).
Proof. Consider a bichain \(\mathfrak{B}:=(V,L_1,L_2)\). We start by the following two facts;
Fact 1: If \(M\) and \(N\) are two linear-modules such that \(M\cap N\neq \varnothing\), then they are with the same kind.
Indeed, the result is immediate when \(M \subseteq N\) or \(N \subseteq M\). Now, assume that \(M\) and \(N\) overlap. In this case, \(|M|\geq2\) and \(|N|\geq 2\). By Lemma 1, \(N\setminus M\) and \(M\setminus N\) are modules of \(\mathfrak{B}\) and hence they are modules of both \(L_1\) and \(L_2\). To the contrary, suppose that \(M\) is positive and \(N\) is negative. It follows that, \(|M\cap N|=1\). Let denote by \(x\) the unique element of \(M\cap N\). Observe that, \(x\) must be the smallest element or the largest one of the linear ordering \(L_{1}\upharpoonright N\) because \(N\setminus M\) is a module of \(L_1\). First, assume that \(x\) is the smallest element of the linear ordering \(L_{1}\upharpoonright N\), i.e \(x<_{L_1} N\setminus M\). Since \(N\) is negative, it follows that \(x\) is also the smallest element of the linear ordering \(L^*_2\upharpoonright N\), i.e \(x<_{L^*_2} N\setminus M\). Recall that a linear ordering and its dual have the same modules. Since \(M\) and \(N\) are modules of both \(L_1\) and \(L_2\), \(M\) and \(N\) are also modules of \(L_1\) and \(L^*_2\). Therefore, the fact that \(x<_{L_1} N\setminus M\) and \(x<_{L^*_2} N\setminus M\), and \(M\) is a module of \(L_1\) and \(L^*_2\) implies that \(M\setminus N<_{L_1} N\setminus M\) and \(M\setminus N<_{L^*_2} N\setminus M\). Since \(N\) is a module of \(L_1\) and \(L^*_2\), \(M\setminus N<_{L_1} x\) and \(M\setminus N<_{L^*_2} x\). Consequently, \(M\setminus N<_{L_1} x\) and \(x <_{L_2} M\setminus N\), which contradicts the fact that \(M\) is positive. Second, assume that \(x\) is the largest element of the linear ordering \(L_{1}\upharpoonright N\). By considering the linear orderings \(L^*_1\) and \(L_2\) instead of \(L_1\) and \(L^*_2\) in what precedes, we obtain a similar contradiction.
Fact 2: If \(M\) and \(N\) are two linear-modules with the same kind such that \(M\cap N\neq \varnothing\), then \(M\cup N\) is a linear-module with the same kind as \(M\) and \(N\).
Indeed, we may assume that \(M\) and \(N\) overlap. Lemma 1 implies that \(M\cup N\), \(M\cap N\), \(M\setminus N\) and \(N\setminus M\) are modules of \(\mathfrak{B}\) and hence they are modules of \(L_1\). Thus, \(N\setminus M<_{L_1} M\cap N\) or \(M\cap N<_{L_1}N\setminus M\). First, assume that \(N\setminus M<_{L_1} M\cap N\). Since \(M\) is a module of \(L_1\), \(N\setminus M<_{L_1} M\setminus N\). Moreover, the fact that \(N\) is a module of \(L_1\) implies that \(M\cap N<_{L_1}M\setminus N\). In other words, \(N\setminus M<_{L_1} M\cap N<_{L_1} M\setminus N\). If \(M\) and \(N\) are both negative (respectively positive), then \(M\setminus N<_{L_2} M\cap N<_{L_2}N\setminus M\) (respectively \(N\setminus M<_{L_2} M\cap N<_{L_2} M\setminus N\)). By transitivity of the linear ordering \(L_2\), \(M\setminus N<_{L_2} N\setminus N\) (respectively \(N\setminus M<_{L_2}M\setminus N\)). Thus, \(M\cup N\) is a negative linear-module (respectively positive linear-module) of \(\mathfrak{B}\). Second, assume that \(M\cap N<_{L_1}N\setminus M\). The fact that \(M\) and \(N\) are modules of \(L_1\) implies that \(M\setminus N<_{L_1} N\setminus M\) and \(M\setminus N<_{L_1}M\cap N\). In other words, \(M\setminus N<_{L_1} M\cap N<_{L_1} N\setminus M\). If \(M\) and \(N\) are both negative (respectively positive), then \(N\setminus M<_{L_2} M\cap N<_{L_2}M\setminus N\) (respectively \(M\setminus N<_{L_2} M\cap N<_{L_2} N\setminus M\)). By transitivity of the linear ordering \(L_2\), \(N\setminus M<_{L_2} M\setminus N\) (respectively \(M\setminus N<_{L_2}N\setminus M\)). Thus, \(M\cup N\) is a negative linear-module (respectively positive linear-module) of \(\mathfrak{B}\).
Now, let us prove the first assertion. Let denote by \(\mathcal{U}\) the union of some collection \(\mathcal{C}_x\) of linear-modules containing a given vertex \(x\). We will prove that \(\mathcal{U}\) is also a linear-module. Clearly, by Lemma 1, \(\mathcal{U}\) is a module of \(\mathfrak{B}\). By Fact 1, all the members of \(\mathcal{C}_x\) are with the same kind. First, assume that all the members of \(\mathcal{C}_x\) are positive. We will prove that \(\mathcal{U}\) is positive. Let \(a\neq b\in \mathcal{U}\). There exist two members \(A\) and \(B\) of \(\mathcal{C}_x\) such that \(a\in A\) and \(b\in B\). By Fact 2, \(A\cup B\) is positive and hence \(L_{2}\upharpoonright \{a,b\}=L_{1}\upharpoonright \{a,b\}\). It follows that, \(L_{2}\upharpoonright \mathcal{U}=L_{1}\upharpoonright \mathcal{U}\). Second, assume that all the members of \(\mathcal{C}_x\) are negative. We will prove that \(\mathcal{U}\) is negative. Let \(a\neq b\in \mathcal{U}\). There exist two members \(A\) and \(B\) of \(\mathcal{C}_x\) such that \(a\in A\) and \(b\in B\). Fact 2 implies that \(A\cup B\) is negative, and hence \(L_{2}\upharpoonright \{a,b\}=L^*_{1}\upharpoonright \{a,b\}\). It follows that, \(L_{2}\upharpoonright \mathcal{U}=L^*_{1}\upharpoonright \mathcal{U}\).
Since each singleton of the vertex set of \(\mathfrak{B}\) is a non-empty linear-module of \(\mathfrak{B}\), the last assertion is an immediate consequence of the second one. Finally, let us prove the second assertion. Consider a non-empty linear-module \(M\) of \(\mathfrak{B}\). By the first assertion, the collection of all linear-modules including \(M\) is a linear-module with the same kind of \(M\) and thus it is the unique maximal one containing it. ◻
Notation 3.
A finite bichain \(\mathfrak{B}:=(\{x_1,\dots,x_n\},L_1,L_2)\) will be denoted by \(\begin{pmatrix} x_{\sigma_1(1)}&x_{\sigma_1(2)}&\dots& x_{\sigma_1(n)}\\ x_{\sigma_2(1)}&x_{\sigma_2(2)}&\dots & x_{\sigma_2(n)} \end{pmatrix}\), where \(\sigma_1\) and \(\sigma_2\) are the permutations of the set \(\{1,\dots,n\}\) such that \(L_1:= x_{\sigma_1(1)} <x_{\sigma_1(2)}<\dots <x_{\sigma_1(n)}\) and \(L_2:= x_{\sigma_2(1)} <x_{\sigma_2(2)}<\dots <x_{\sigma_2(n)}\).
Given a bichain \(\mathfrak{B}:=(V,L_1,L_2)\), let \(M\) be a vertex subset of \(\mathfrak{B}\) and \(x\) be an element of \(V\setminus M\).
Write \(x\sim M\), if \(M\) is a module of \(\mathfrak{B}\upharpoonright M\cup \{x\}\) and \(x\nsim M\) otherwise.
The set \(\{\{a,b\},a\neq b \in V \ such \ that \ L_2\upharpoonright \{a,b\}=L^*_1\upharpoonright \{a,b\} \}\) will be denoted simply by \(I(\mathfrak{B})\).
The lemma below is easily checked;
Lemma 5. Let \(\mathfrak{B}\) be a bichain with three vertices \(x\), \(y\) and \(z\). Then \(\mathfrak{B}\) is isomorphic to one of the nonisomorphic following bichains, \(\begin{pmatrix} x&y&z\\ x&y&z \end{pmatrix}\), \(\begin{pmatrix} x&y&z\\ z&y&x \end{pmatrix}\), \(\begin{pmatrix} x&y&z\\ z&x&y \end{pmatrix}\), \(\begin{pmatrix} x&y&z\\ x&z&y \end{pmatrix}\), \(\begin{pmatrix} x&y&z\\ y&x&z \end{pmatrix}\) and \(\begin{pmatrix} x&y&z\\ y&z&x \end{pmatrix}\).
Remark 5.
Given a bichain \(\mathfrak{B}\) on a set \(V\), \(\mathfrak{B}\) is positive linear ( respectively negative linear) if and only if \(I(\mathfrak{B})=\varnothing\) ( respectively \(I(\mathfrak{B})\) is the set of all the 2-element subsets of \(V\)).
Given a positive integer \(n\), up to isomorphism, there are a unique positive linear-bichain and a unique negative linear-bichain, with \(n\) vertices. These two linear-bichains are non isomorphic when \(n\geq2\).
Let \(\mathfrak{B}\) and \(\mathfrak{B'}\) be two bichains on a set \(V\). \(\mathfrak{B}\) and \(\mathfrak{B'}\) are \((\leq 2)\)-hypomorphic if and only if \(I(\mathfrak{B})=I(\mathfrak{B'})\).
A non linear-bichain on a 3-element set has a unique non trivial module.
Given a non linear-bichain \(\mathfrak{B}\) on a set \(\{a,b,c\}\), consider its unique non trivial module \(M\). For each 2-element vertex subset \(X\neq M\), there is a unique \(i\in \{1,2\}\) such that \(y\nsim_{L_i} X\) where \(\{y\}=\{a,b,c\}\setminus X\).
Proof. The first assertion is easily checked by definitions of positive and negative linear-bichain. The second assertion is an immediate consequence of the first one. The third assertion follows from the definition of the \((\leq 2)\)-hypomorphic bichains. The fourth and fifth assertions are easily checked by examining the four cases of non linear-bichains introduced in Lemma 5. ◻
The following useful corollary is immediately deduced from Remark 5;
Corollary 4. Let \(\mathfrak{B}\) be a linear-bichain on a set \(V\), and \(\mathfrak{B'}\) be a bichain on \(V\). If \(\mathfrak{B'}\) is \((\leq 2)\)-hypomorphic to \(\mathfrak{B}\), then \(\mathfrak{B'}\) is linear with the same kind as \(\mathfrak{B}\), and \(\mathfrak{B'}\upharpoonright X\simeq \mathfrak{B}\upharpoonright X\) for each finite vertex subset \(X\).
Corollary 5. Let \(\mathfrak{B}:=(\{x,y,z\},L_1,L_2)\) be a bichain with three vertices. If \(x \sim_{L_i}\{y,z\}\) and \(x \nsim_{L_j}\{y,z\}\) where \(\{i,j\}=\{1,2\}\), then \(\mathfrak{B}\) is not linear.
Proof. This result follows from the fact that if \(\mathfrak{B}\) is a linear-bichain, then \(L_1\) and \(L_2\) have the same modules. ◻
Lemma 6. Let \(\mathfrak{B}\) and \(\mathfrak{B'}\) be \((\leq 3)\)-hypomorphic bichains with three vertices \(x,y\) and \(z\). Then the following assertions hold.
If \(\mathfrak{B}:=\begin{pmatrix} x&y&z\\ x&y&z \end{pmatrix}\), then \(\mathfrak{B'}\) is one of the six positive linear-bichains on \(\{x,y,z\}\).
If \(\mathfrak{B}:=\begin{pmatrix} x&y&z\\ z&y&x \end{pmatrix}\), then \(\mathfrak{B'}\) is one of the six negative linear-bichains on \(\{x,y,z\}\).
If \(\mathfrak{B}:=\begin{pmatrix} x&y&z\\ z&x&y \end{pmatrix}\), then \(\mathfrak{B'}=\mathfrak{B}\) or \(\mathfrak{B'}:=\begin{pmatrix} y&x&z\\ z&y&x \end{pmatrix}\).
If \(\mathfrak{B}:=\begin{pmatrix} x&y&z\\ x&z&y \end{pmatrix}\), then \(\mathfrak{B'}=\mathfrak{B}\) or \(\mathfrak{B'}:=\begin{pmatrix} x&z&y\\ x&y&z \end{pmatrix}\).
If \(\mathfrak{B}:=\begin{pmatrix} x&y&z\\ y&x&z \end{pmatrix}\), then \(\mathfrak{B'}=\mathfrak{B}\) or \(\mathfrak{B'}:=\begin{pmatrix} y&x&z\\ x&y&z \end{pmatrix}\).
If \(\mathfrak{B}:=\begin{pmatrix} x&y&z\\ y&z&x \end{pmatrix}\), then \(\mathfrak{B'}=\mathfrak{B}\) or \(\mathfrak{B'}:=\begin{pmatrix} x&z&y\\ z&y&x \end{pmatrix}\).
Proof. First, let us prove the first and the second assertions. In that cases, observe that \(\mathfrak{B}\) is a linear-bichain on \(\{x,y,z\}\). Since \(\mathfrak{B'}\) is \((\leq 3)\)-hypomorphic to \(\mathfrak{B}\), \(\mathfrak{B'}\) is a linear-bichain with the same kind as \(\mathfrak{B}\) by Corollary 4. Consequently, if \(\mathfrak{B}:=\begin{pmatrix} x&y&z\\ x&y&z \end{pmatrix}\), i.e. \(\mathfrak{B}\) is a positive linear-bichain, then \(\mathfrak{B'}\) is one of the six positive linear-bichains on \(\{x,y,z\}\). If \(\mathfrak{B}:=\begin{pmatrix} x&y&z\\ z&y&x \end{pmatrix}\), i.e. \(\mathfrak{B}\) is a negative linear-bichain, then \(\mathfrak{B'}\) is one of the six negative linear-bichains on \(\{x,y,z\}\).
Second, for the other assertions the proof follows immediately from Lemma 5 and the first assertion of Remark 5. For instance, let us prove the third assertion. Let \(\mathfrak{B}:=\begin{pmatrix} x&y&z\\ z&x&y \end{pmatrix}\). Since \(\mathfrak{B'}\) is \((\leq 3)\)-hypomorphic to \(\mathfrak{B}\), \(\mathfrak{B'}\simeq \mathfrak{B}\). Consequently, by Lemma 5, \(\mathfrak{B'}\) is one of the following isomorphic bichains: \(\begin{pmatrix} x&y&z\\ z&x&y \end{pmatrix}\), \(\begin{pmatrix} x&z&y\\ y&x&z \end{pmatrix}\), \(\begin{pmatrix} y&x&z\\ z&y&x \end{pmatrix}\), \(\begin{pmatrix} y&z&x\\ x&y&z \end{pmatrix}\), \(\begin{pmatrix} z&x&y\\ y&z&x \end{pmatrix}\) or \(\begin{pmatrix} z&y&x\\ x&z&y \end{pmatrix}\). Moreover, Remark 5 implies that \(I(\mathfrak{B})=I(\mathfrak{B'})\). It follows that, \(\mathfrak{B'}=\mathfrak{B}\) or \(\mathfrak{B'}:= \begin{pmatrix} y&x&z\\ z&y&x \end{pmatrix}\). ◻
The following useful corollary is immediately deduced from Lemma 6;
Corollary 6. Let \(\mathfrak{B}:=(\{x,y,z\}, L_1,L_2)\) and \(\mathfrak{B'}:=(\{x,y,z\}, L'_1,L'_2)\) be \((\leq 3)\)-hypomorphic bichains with three vertices such that \(\mathfrak{B}\) is not linear where \(\{x,y\}\) is its unique non trivial module. Then \(\mathfrak{B}\upharpoonright \{t,z\}=\mathfrak{B'}\upharpoonright \{t,z\}\), for all \(t\in \{x,y\}\).
Notation 4. Given a bichain \(\mathfrak{B}:=(V,L_1,L_2)\) on a set \(V\), let \(M\) be a proper vertex subset and x be an element of \(V\setminus M\). Write
\(S^{x}_1=\{\) }.
\(S^{x}_2=\{\)}.
Lemma 7. Given a bichain \(\mathfrak{B}:=(V,L_1,L_2)\), a maximal linear-module \(M\) of \(\mathfrak{B}\), and \(x\in V\setminus M\) such that \(M \cup \{x\}\) is linear, one of the following assertions holds.
\(S^{x}_1\setminus S^{x}_2\neq \varnothing\), the bichain \(\mathfrak{B}\upharpoonright\{a,x,y\}\) is not linear, and \(\{a,x\}\) is not a module of \(\mathfrak{B}\upharpoonright\{a,x,y\}\), for any vertices \(a\) and \(y\) where \(a\in M\) and \(y \in S^{x}_1\setminus S^{x}_2\).
\(S^{x}_2\setminus S^{x}_1\neq \varnothing\), the bichain \(\mathfrak{B}\upharpoonright\{a,x,y\}\) is not linear, and \(\{a,x\}\) is not a module of \(\mathfrak{B}\upharpoonright\{a,x,y\}\), for any vertices \(a\) and \(y\) where \(a\in M\) and \(y \in S^{x}_2\setminus S^{x}_1\).
\(S^{x}_1= S^{x}_2\neq \varnothing\) and there are \(y\neq z\in S^{x}_1\) with \(y<_{L_1}z\) such that, for all \(a\in M\), the bichain \(\mathfrak{B}\upharpoonright\{a,x,y,z\}\) is one of the following bichains: \(\begin{pmatrix} a&y&z&x\\ a&z&y&x \end{pmatrix}\), \(\begin{pmatrix} x&y&z&a\\ x&z&y&a \end{pmatrix}\), \(\begin{pmatrix} a&y&z&x\\ x&y&z&a \end{pmatrix}\) or \(\begin{pmatrix} x&y&z&a\\ a&y&z&x \end{pmatrix}\).
Proof. Consider a bichain \(\mathfrak{B}:=(V,L_1,L_2)\), and a maximal
linear-module \(M\) of \(\mathfrak{B}\). Let \(x\in V\setminus M\) such that \(M\cup \{x\}\) is linear, and \(a\in M\). Since \(M\) is a maximal linear-module and \(M\cup \{x\}\) is linear, \(M\cup \{x\}\) is not a module of \(\mathfrak{B}\). Thus, \(S^x_1 \cup S^x_2\neq \varnothing\). It
follows that, \(S^{x}_1\setminus S^{x}_2\neq
\varnothing\) or \(S^{x}_2\setminus
S^{x}_1\neq \varnothing\) or \(S^{x}_1=
S^{x}_2\neq \varnothing\).
For the first assertion, assume that \(S^{x}_1\setminus S^{x}_2\neq \varnothing\).
Let \(y\in S^{x}_1\setminus S^{x}_2\).
Clearly, \(y\nsim_{L_1}\{a,x\}\) and
\(y\sim_{L_2}\{a,x\}\). Thus, \(\{a,x\}\) is not a module of \(\mathfrak{B}\upharpoonright \{a,x,y\}\). By
Corollary 5, \(\mathfrak{B}\upharpoonright\{a,x,y\}\) is
not linear.
For the second assertion, assume that \(S^{x}_2\setminus S^{x}_1\neq \varnothing\). Let \(y\in S^{x}_2\setminus S^{x}_1\). Clearly, \(y\sim_{L_1}\{a,x\}\) and \(y\nsim_{L_2}\{a,x\}\). Thus, \(\{a,x\}\) is not a module of \(\mathfrak{B}\upharpoonright \{a,x,y\}\). By Corollary 5, \(\mathfrak{B}\upharpoonright\{a,x,y\}\) is not linear.
For the third assertion, assume that \(S^{x}_1= S^{x}_2\neq \varnothing\). Let \(t\in V\setminus (M\cup S^{x}_1\cup\{x\})\). Let \(i\in\{1,2\}\). Since ( \(M<_{L_i}S^{x}_1<_{L_i}x\) or \(x<_{L_i}S^{x}_1<_{L_i}M\)) and \(t\sim_{L_i}M\cup \{x\}\) because \(t\notin S^{x}_1\), \(t\sim_{L_i}M\cup S^{x}_1\) and \(x\sim_{L_i}M\cup S^{x}_1\). It follows that, \(M\cup S^{x}_1\) is a module of \(\mathfrak{B}\). Since \(M\) is a maximal linear-module of \(\mathfrak{B}\), \(M\cup S^{x}_1\) is not linear. First, assume that \(M\cup\{x\}\) is positive. We claim that there are \(y\neq z\in S^{x}_1\) with \(y<_{L_1}z\) such that \(\{y,z\} \in I(\mathfrak{B}\upharpoonright S^{x}_1)\). Indeed, otherwise, \(M\cup S^{x}_1\) is positive, and then it is a positive linear-module of \(\mathfrak{B}\); witch contradicts the maximality of \(M\). Thus, the bichain \(\mathfrak{B}\upharpoonright \{a,x,y,z\}\) is one of the following bichains: \(\begin{pmatrix} a&y&z&x\\ a&z&y&x \end{pmatrix}\), \(\begin{pmatrix} x&y&z&a\\ x&z&y&a \end{pmatrix}\). Second, assume that \(M\cup \{x\}\) is negative. We claim that there are \(y\neq z\in S^{x}_1\) with \(y<_{L_1}z\) such that \(\{y,z\}\notin I(\mathfrak{B}\upharpoonright S^{x}_1)\). Indeed, otherwise, \(M\cup S^{x}_1\) is negative, and then it is a negative linear-module of \(\mathfrak{B}\); witch contradicts the maximality of \(M\). Thus, the bichain \(\mathfrak{B}\upharpoonright \{a,x,y,z\}\) is one of the following bichains: \(\begin{pmatrix} a&y&z&x\\ x&y&z&a \end{pmatrix}\), \(\begin{pmatrix} x&y&z&a\\ a&y&z&x \end{pmatrix}\). ◻
Lemma 8. Let \(\mathfrak{B}\) and \(\mathfrak{B'}\) be \((\leq 3)\)-hypomorphic bichains on the same vertex set \(V\), and \(M\) be a maximal linear-module of \(\mathfrak{B}\). Then \(\mathfrak{B'}\upharpoonright \{a,x\}=\mathfrak{B}\upharpoonright \{a,x\}\), for any vertices \(a,x\) with \(a\in M\) and \(x\in V\setminus M\).
Proof. Consider two \((\leq
3)\)-hypomorphic bichains \(\mathfrak{B}:=(V,L_1,L_2)\) and \(\mathfrak{B'}:=(V,L'_1,L'_2)\).
Let \(x\in V\setminus M\) and \(a\in M\). According to the linearity of
\(M\cup \{x\}\) in \(\mathfrak{B}\), we distinguish the
following two cases.
Case 1: Assume that \(M\cup\{x\}\) is not linear.
In this case, \(|M|\geq 2\). If
\(M\) is positive, then \(x<_{L_1}M\Leftrightarrow M<_{L_2}x\).
If \(M\) is negative, then \(x<_{L_1}M\Leftrightarrow x<_{L_2}M\).
It follows that, for all \(b\in M\setminus
\{a\}\) \(\mathfrak{B} \upharpoonright
\{a,b,x\}\) is not linear and \(\{a,b\}\) is the unique non trivial
linear-module of \(\mathfrak{B}
\upharpoonright \{a,b,x\}\). Thus, Corollary 6 implies that \(\mathfrak{B'}\upharpoonright
\{a,x\}=\mathfrak{B}\upharpoonright \{a,x\}\).
Case 2: Assume that \(M\cup\{x\}\) is linear.
Since \(M\cup\{x\}\) is linear, Lemma 7 implies that one of its assertions holds. First, assume that assertion (1) holds. Let \(y\in S^{x}_1\setminus S^{x}_2\). The bichain \(\mathfrak{B}\upharpoonright \{a,x,y\}\) is not linear and \(\{a,x\}\) is not a module of \(\mathfrak{B}\upharpoonright \{a,x,y\}\). Thus, Corollary 6 implies that \(\mathfrak{B'}\upharpoonright \{a,x\}=\mathfrak{B}\upharpoonright \{a,x\}\). Second, assume that assertion (2) holds. Let \(y\in S^{x}_2\setminus S^{x}_1\). The bichain \(\mathfrak{B}\upharpoonright \{a,x,y\}\) is not linear and \(\{a,x\}\) is not a module of \(\mathfrak{B}\upharpoonright \{a,x,y\}\). Thus, Corollary 6 implies that \(\mathfrak{B'}\upharpoonright \{a,x\}=\mathfrak{B}\upharpoonright \{a,x\}\). Finally, assume that assertion (3) holds. Let \(y\neq z\in S^{x}_1\) with \(y<_{L_1}z\) such that the bichain \(\mathfrak{B}\upharpoonright \{a,x,y,z\}\) is one of the following bichains: \(\begin{pmatrix} a&y&z&x\\ a&z&y&x \end{pmatrix}\), \(\begin{pmatrix} x&y&z&a\\ x&z&y&a \end{pmatrix}\), \(\begin{pmatrix} a&y&z&x\\ x&y&z&a \end{pmatrix}\) or \(\begin{pmatrix} x&y&z&a\\ a&y&z&x \end{pmatrix}\). Observe that, \(\mathfrak{B}\upharpoonright \{a,y,z\}\) and \(\mathfrak{B}\upharpoonright \{x,y,z\}\) are not linear-bichains and \(\{y,z\}\) is the unique non trivial linear-module of \(\mathfrak{B}\upharpoonright \{a,y,z\}\) and \(\mathfrak{B}\upharpoonright \{x,y,z\}\). By Corollary 6, it follows that \(\mathfrak{B'}\upharpoonright \{a,t\}=\mathfrak{B}\upharpoonright \{a,t\}\) and \(\mathfrak{B'}\upharpoonright \{t,x\}=\mathfrak{B}\upharpoonright \{t,x\}\), for all \(t\in \{y,z\}\). Now, let \(t\in\{y,z\}\). Assume for instance that \(\{a, x\}\) is positive and let \(i\in\{1,2\}\). If \(a<_{L_1}t<_{L_1}x\) (respectively \(x<_{L_1}t<_{L_1} a\)), then \(a<_{L'_i}t\) and \(t<_{L'_i}x\) (respectively \(x<_{L'_i}t\) and \(t <_{L'_i} a\)) because \(\mathfrak{B'}\upharpoonright \{a,t\}=\mathfrak{B}\upharpoonright \{a,t\}\) and \(\mathfrak{B'}\upharpoonright \{t,x\}=\mathfrak{B}\upharpoonright \{t,x\}\). Thus, by transitivity of the linear orderings \(L'_1\) and \(L'_2\) we deduce that \(\mathfrak{B'}\upharpoonright \{a,x\}=\mathfrak{B}\upharpoonright \{a,x\}\). By the same reasoning in what precedes we obtain that \(\mathfrak{B'}\upharpoonright \{a,x\}=\mathfrak{B}\upharpoonright \{a,x\}\), when \(\{a,x\}\) is negative. ◻
Consider two \((\leq 3)\)-hypomorphic bichains \(\mathfrak{B}\) and \(\mathfrak{B'}\) on the same vertex set \(V\). By Lemma 4, the maximal linear-modules of \(\mathfrak{B}\) ( respectively \(\mathfrak{B'}\)) form a partition of \(V\). Denote by \(\mathcal{Q}\) and \(\mathcal{Q'}\) the partition of \(V\) into maximal linear-modules of \(\mathfrak{B}\) and \(\mathfrak{B'}\) respectively. Consider an element \(M\) of \(\mathcal{Q}\). First, we will prove that \(M\) is a linear-module of \(\mathfrak{B'}\). Clearly, if \(|M|=1\), the result is obvious. Now, assume that \(|M|\geq 2\). Since \(\mathfrak{B}\) and \(\mathfrak{B'}\) are \((\leq 3)\)-hypomorphic and \(\mathfrak{B}\upharpoonright M\) is linear, by Corollary 4 \(\mathfrak{B'}\upharpoonright M\) is linear with the same kind as \(\mathfrak{B}\upharpoonright M\). Now, consider an element \(x\) of \(V\setminus M\). By Lemma 8, \(\mathfrak{B'}\upharpoonright \{a,x\}=\mathfrak{B}\upharpoonright \{a,x\}\), for all \(a\in M\). Moreover, \(x \sim M\) in \(\mathfrak{B}\) because \(M\) is a module of \(\mathfrak{B}\). It follows that, \(x \sim M\) in \(\mathfrak{B'}\) and hence \(M\) is a linear-module of \(\mathfrak{B'}\). In conclusion, each element of \(\mathcal{Q}\) is a linear-module of \(\mathfrak{B'}\). By interchanging \(\mathfrak{B}\) and \(\mathfrak{B'}\), it follows that each element of \(\mathcal{Q'}\) is a linear-module of \(\mathfrak{B}\). Second, we will prove that \(M\) is also a maximal linear-module of \(\mathfrak{B}'\). Let \(M'\) be an element of \(\mathcal{Q'}\) including \(M\). Since \(M'\) is a linear-module of \(\mathfrak{B}\), there is an element \(M''\) of \(\mathcal{Q}\) including \(M'\). Consequently, \(M''=M'=M\), and hence \(M\in \mathcal{Q'}\) which permits to conclude. Therefore, \(\mathcal{Q'}=\mathcal{Q}\). Finally, by Lemma 8 the quotient bichains \(\mathfrak{B}/\mathcal{Q}\) and \(\mathfrak{B'}/\mathcal{Q}\) are equal.
Conversely, consider two bichains \(\mathfrak{B}\) and \(\mathfrak{B'}\) on the same vertex set \(V\), having the same modular partition \(\mathcal{Q}\) on maximal linear-modules such that \(\mathfrak{B}/\mathcal{Q}=\mathfrak{B'}/\mathcal{Q}\), and each maximal linear-module has the same kind in both. We have to prove that \(\mathfrak{B}\) and \(\mathfrak{B'}\) are \((\leq 3)\)-hypomorphic. Let \(M\in \mathcal{Q}\). Since \(\mathfrak{B}\upharpoonright M\) and \(\mathfrak{B'}\upharpoonright M\) are linear with the same kind, \(\mathfrak{B}\upharpoonright M\) and \(\mathfrak{B'}\upharpoonright M\) are \((\leq 3)\)-hypomorphic. Thus, Lemma 2 implies that the bichains \(\mathfrak{B}\) and \(\mathfrak{B'}\) are \((\leq 3)\)-hypomorphic.
In this subsection we give a characterization of the \((\leq 3)\)-reconstructible posets based on a description of the maximal chain-modules. We use essentially the following lemma which is an immediate consequence of Lemma 2 of [15] deduced from the study of Boudabbous and Delhommé [7].
Lemma 9. [15]
The family of maximal chain-modules of a poset \(P\) is a modular partition of \(P\).
If \(X\) is an infinite set, then there are at least two nonisomorphic chains on \(X\).
Corollary 7. A poset is \((\leq 3)\)-reconstructible if and only if its chain-modules are finite.
Proof. Assume that a poset \(P\) has an infinite chain-module. By the first assertion of Lemma 9, the family \(\mathcal{M}\) of maximal chain-modules of \(P\) forms a modular partition of \(P\). Consider the family \(\mathcal{F}\) of such maximal chain-modules having a same infinite cardinality \(\mathcal{K}\). By the second assertion of Lemma 9 there are two nonisomorphic chains \(\mathbf{c}_0\) and \(\mathbf{c}_1\) with cardinality \(\mathcal{K}\). Consider the following poset \(P_0\) ( respectively \(P_1\)) obtained from \(P\) by replacing \(P\upharpoonright A\) by a chain isomorphic to \(\mathbf{c}_0\) ( respectively \(\mathbf{c}_1\)), for each \(A\in \mathcal{F}\). Now, let us prove that \(P_0\) and \(P_1\) are \((\leq 3)\)-hypomorphic to \(P\). Clearly, \(\mathcal{M}\) is a common modular partition of \(P\), \(P_0\) and \(P_1\) with \(P/\mathcal{M}=P_0/\mathcal{M}=P_1/\mathcal{M}\). Moreover, for each \(M\in \mathcal{M}\), \(P\upharpoonright M\), \(P_0\upharpoonright M\) and \(P_1\upharpoonright M\) are chains, and hence they are \((\leq 3)\)-hypomorphic. Thus, Lemma 2 implies that \(P\), \(P_0\) and \(P_1\) are \((\leq3)\)-hypomorphic. Consequently, by Theorem 1, \(\mathcal{M}\) is a common partition into maximal chain-modules of \(P\), \(P_0\) and \(P_1\). Since \(\mathbf{c}_0\) and \(\mathbf{c}_1\) are not isomorphic, \(P_0\) and \(P_1\) are not isomorphic. Therefore, at least one of the posets \(P_0\) and \(P_1\) is not isomorphic to \(P\), and hence \(P\) is not \((\leq 3)\)-reconstructible.
Conversely, let \(P\) be a poset with a vertex set \(V\), and assume that its maximal chain-modules are finite. Let \(P'\) be a poset \((\leq 3)\)-hypomorphic to \(P\). We shall prove that \(P\) and \(P'\) are isomorphic. By Theorem 1, \(P\) and \(P'\) share the same maximal chain-modules, and they have the same corresponding quotient relation. Since the maximal chain-modules are finite, \(P\upharpoonright M\) and \(P'\upharpoonright M\) are isomorphic for each maximal chain-module \(M\) of \(P\). Finally, by Lemma 2, \(P\) and \(P'\) are isomorphic. ◻
In this subsection we give a characterization of the \((\leq 3)\)-reconstructible bichains based on a description of the maximal linear-modules.
Corollary 8. A bichain is \((\leq 3)\)-reconstructible if and only if its linear-modules are finite.
Proof. Assume that a bichain \(\mathfrak{B}\) has an infinite linear-module. By Lemma 4, the family \(\mathcal{M}\) of maximal linear-modules of \(\mathfrak{B}\) forms a modular partition of \(\mathfrak{B}\). Consider the family \(\mathcal{F}\) of such maximal linear-modules having a same infinite cardinality \(\mathcal{K}\). By the second assertion of Lemma 9 there are two nonisomorphic linear orderings \(\mathbf{c}_0\) and \(\mathbf{c}_1\) with cardinality \(\mathcal{K}\). Consider the following bichain \(\mathfrak{B_0}\) ( respectively \(\mathfrak{B_1}\)) obtained from \(\mathfrak{B}\) by replacing \(\mathfrak{B}\upharpoonright A\) by a bichain isomorphic to \(\begin{pmatrix} \mathbf{c}_0\\ \mathbf{c}_0 \end{pmatrix}\) \(\Bigg(\) respectively \(\begin{pmatrix} \mathbf{c}_1\\ \mathbf{c}_1 \end{pmatrix}\)\(Bigg)\) for each \(A\) in \(\mathcal{F}\) such that \(A\) is positive, and by a bichain isomorphic to \(\begin{pmatrix} \mathbf{c}_0\\ \mathbf{c^*}_0 \end{pmatrix}\) \(\Bigg(\) respectively \(\begin{pmatrix} \mathbf{c}_1\\ \mathbf{c^*}_1 \end{pmatrix}\)\(\Bigg)\) for each \(A\) in \(\mathcal{F}\) such that \(A\) is negative. Now, let us prove that \(\mathfrak{B}_0\) and \(\mathfrak{B}_1\) are \((\leq 3)\)-hypomorphic to \(\mathfrak{B}\). \(\mathcal{M}\) is a common modular partition of \(\mathfrak{B}\), \(\mathfrak{B}_0\) and \(\mathfrak{B}_1\) with \(\mathfrak{B}/\mathcal{M}=\mathfrak{B}_0/\mathcal{M}=\mathfrak{B}_1/\mathcal{M}\). Moreover, for each \(M\in \mathcal{M}\), the bichains \(\mathfrak{B}\upharpoonright M\), \(\mathfrak{B}_0\upharpoonright M\) and \(\mathfrak{B}_1\upharpoonright M\) are linear with the same kind, and hence they are \((\leq 3)\)-hypomorphic. Thus, Lemma 2 implies that the bichains \(\mathfrak{B}\), \(\mathfrak{B}_0\) and \(\mathfrak{B}_1\) are \((\leq3)\)-hypomorphic. Consequently, by Theorem 2, \(\mathcal{M}\) is a common partition into maximal linear-modules of \(\mathfrak{B}\), \(\mathfrak{B}_0\) and \(\mathfrak{B}_1\). Since the linear orderings \(\mathbf{c}_0\) and \(\mathbf{c}_1\) are not isomorphic, \(\mathfrak{B}_0\) and \(\mathfrak{B}_1\) are not isomorphic. Therefore, at least one of the bichains \(\mathfrak{B}_0\) and \(\mathfrak{B}_1\) is not isomorphic to \(\mathfrak{B}\), and hence \(\mathfrak{B}\) is not \((\leq 3)\)-reconstructible.
Conversely, let \(\mathfrak{B}\) be a bichain with a vertex set \(V\), and assume that its maximal linear-modules are finite. Consider a bichain \(\mathfrak{B'}\) \((\leq 3)\)-hypomorphic to \(\mathfrak{B}\) on the same vertex set \(V\). We shall prove that \(\mathfrak{B}\) and \(\mathfrak{B'}\) are isomorphic. By Theorem 2, \(\mathfrak{B}\) and \(\mathfrak{B'}\) share the same maximal linear-modules, and they have the same corresponding quotient bichain and each maximal linear-module has the same kind in both. Since the maximal linear-modules of \(\mathfrak{B}\) are finite, \(\mathfrak{B}\upharpoonright M\simeq \mathfrak{B'}\upharpoonright M\) for each maximal linear-module \(M\) of \(\mathfrak{B}\). Finally, by Lemma 2, \(\mathfrak{B}\) and \(\mathfrak{B'}\) are isomorphic. ◻
The authors are indebted to the referee for his/her useful suggestions critical comments.
The author declares no conflict of interests.